Reducibility of Quartic Polynomials and its Relation to Galois Groups

Jinhe Huang^1, *, Yicheng Ai², Yuhao Wen³

¹The Experimental High School Attached to Beijing Normal University, Beijing, 100032, China

²Tsinglan School, Dongguan, 523808, China

³Department of Mathematics, University of London, WC1E 6 bt, China

*Corresponding author email: yanhuangheshi@163.com

Abstract. This paper deals with special classes of quartic polynomials and properties pertaining to their Galois groups and reducibility over certain fields. The existence of quartic polynomials irreducible over Q but reducible over every prime field is first proven, after which criteria are established for the Galois group of polynomials with this property. By constructing classes of V₄-generic polynomials and comparing them with criteria put forth in previous studies for determining polynomials with this property, it can be shown that a polynomial of the biquadratic form x⁴ + ax² + b has this property if and only if it can be written as \( {x^{4}} - 2(u + v){x^{2}} + {(u -v)^{2}} \) with u, v ∈ \( Q \) such that none of u, v, or uv can be expressed as ratio of two squares, and 2(u+v),(u−v)² ∈ \( Z \) . The general form for biquadratic polynomials irreducible over \( Q \) and reducible modulo every integer n is found to have a general form similar to this one.

1 Introduction

The relation between polynomials has been an interesting topic for mathematicians in the past few decades.

Several previous studies focused on how to represent groups such as S_n and A_n as Galois groups of polynomials ([1], [2] and [3]), and others tried to find out properties about these polynomials [4]. Among these studies, we found that the reducibility of quartic polynomials is especially appropriate for us to investigate. Both Rotman ([5], p66) and Driver et.[6] included this topic in their researches. This paper aims to review some important properties of quartic polynomials and open up room for further exploration.

We expand on problems put forward in the textbooks of Rotman[5] as well as Dummit and Foote[7] about classifying the family of quartic polynomials that are reducible in all prime fields. Additionally, we address the question of constructing a generic polynomial for a given Galois group - something which is of high relevance to the inverse Galois problem.

2 Polynomials reducible modulo every prime p

The topic of polynomials irreducible over \( Q \) but reducible modulo every prime number p is a recurring concept in textbooks of Galois Theory: the works of Dummit and Foote, Milne[8], and Rotman have all touched on and discussed its properties. For convenience, we shall call polynomials with this property hollowin p.

Example 2.1 f(x) = x⁴ + 1

It can be shown, by forming equations from the coefficients of the potential factorizations of f(x), that there exists no factorization of f(x) in \( Q \) . We can also use Eisenstein’s criterion after the substitution x → x + 1 to examine this result.

Now consider f(x) over a finite field \( {Z_{p}} \) , where p is a prime. We wish to check if f(x) is reducible in ( \( Z/pZ \) )[x] for every prime p:

\( {x^{4}}+ 1 \) mod p

Proof 2.1 It can be easily seen that, for p = 2,

\( {x^{4}}+ 1 ≡ {(x + 1)^{4}} \) mod 2

But for p >2, it is more difficult to find a factor for f(x). To further show this, we must rely on the Legendre symbol, which is defined for some integer α coprime to as

\( \begin{cases} \begin{array}{c} (\frac{α}{p})=1 if α≡{X^{2}} mod p \\ (\frac{α}{p})=-1 if α≢{X^{2}} mod p \end{array} \end{cases} \) for X \( ∈ \) \( Z \) _P

Lemma 2.2 Supplement 1 to the Law of Quadratic Reciprocity ([9],Almutieri)

\( (\frac{-1}{P})=\begin{cases} \begin{array}{c} 1, if p≡1 mod 4 \\ -1, if p≡3 mod 4 \end{array} \end{cases} \)

Proof 2.2 This is a simple consequence of Euler’s Criterion, which states that

\( (\frac{-1}{p})={(-1)^{\frac{p-1}{2}}} \)

The result directly follows from this.

Lemma 2.3 Supplement 2 to the Law of Quadratic Reciprocity ([9],Almutieri)

\( (\frac{2}{p})=\begin{cases} \begin{array}{c} 1, if p≡1 or -1 mod 8 \\ -1, if p≡3 or -3 mod 8 \end{array} \end{cases} \)

Proof 2.3 The proof for this is slightly lengthier: denote X to be

\( exp(\frac{πi}{4})=\frac{\sqrt[]{2}}{2}+i\frac{\sqrt[]{2}}{2} \)

\( {X^{4}}=-1 ⇒{X^{-1}}={-X^{3}}=\frac{\sqrt[]{2}}{2}-i\frac{\sqrt[]{2}}{2} \)

\( Let G=X+{X^{-1}}=X-{X^{-3}}=\frac{\sqrt[]{2}}{2}+i\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}-i\frac{\sqrt[]{2}}{2}=\sqrt[]{2} \)

G can therefore be thought of as the integer, if it exists, such that

G² ≡ 2mod p

Consider G^p= X^p+ X^−p mod p. Since X⁸ = (X⁻¹)⁸ = 1, if p ≡ 1 or −1 mod 8, then

X^P+ X^-P = X+ X^-1 = G

if p ≡ 3 or −3 mod 8, then

X^P+ X^-P = X³+ X^-3 = − X^-1 −X = −G

This implies

\( {G^{p}}≡{-1^{\frac{{p^{2}}-1}{8}}}G mod p \)

At the same time,

\( {G^{p}}={G^{p-1}}G={({G^{2}})^{\frac{P-1}{2}}}G={2^{\frac{P-1}{2}}}G≡(\frac{2}{P})G mod p \)

Combining the two above equations, we can get

\( {-1^{\frac{{p^{2}}-1}{8}}}G≡(\frac{2}{p})G mod p \)

\( {-1^{\frac{{p^{2}}-1}{8}}}=(\frac{2}{p}) \)

which is what we want.

Remark 2.4 For Legendre symbols, the property \( (\frac{a}{p})(\frac{b}{p})=(\frac{ab}{p}) \) holds.

This implies \( (\frac{2}{p})(\frac{-1}{p})=(\frac{-2}{p}) \) ,

where \( (\frac{-2}{p})=1 \) if either \( (\frac{-1}{p})=(\frac{-2}{p})=1 or (\frac{-1}{p})=(\frac{-2}{p})=-1 \)

The first case holds if p ≡ 1 mod 4 and p ≡ 1 or −1 mod 8, so it is true when

p ≡ 1mod 8

The second case holds if p ≡ 3 mod 4 and p ≡ 3 or −3 mod 8, so it is true when

p ≡ 3mod 8

Going back to x⁴+1 mod p, we now see that we can consider three possible cases based on the possible modular values of p:

p ≡ 1 or −1 mod 8 ∃α :α= 2, then

x⁴+1 ≡ x⁴+2x²+1−2x² ≡ (x² + 1) ²−α² ≡ (x²−α+1)(x²+α+1)mod p

p ≡ 3 mod 8 ∃α :α² = −2, then

x⁴+1 ≡ x⁴−2x²+1+2x² ≡ (x² − 1)²−α² ≡ (x²−α−1)(x²+α−1)mod p

p ≡ 1 mod 4 ∃α :α² = −1, then x⁴ + 1 ≡ x⁴ − (α²) ≡ (x² −α)(x² + α) mod p

It should be obvious that every odd prime p will fall into one of the categories listed above. Therefore, we have shown that f(x) is reducible modulo every prime.

Using the same approach, it follows that g(x) = x⁴ + γ⁴ for some γ ∈ \( Z \) are hollow, but can we classify any other such polynomials besides g(x)? Let us exclusively examine hollow polynomials of degree 4.

Example 2.5 ² Determine whether f(x) = x⁴ − 10x² + 1 is hollow.

We notice that the coefficient of the x³ and x terms are 0, meaning we can f(x) as either

(x −a)(x³ + ax² + bx + ab),

or

(x² −ax + b)(x² + ax + b),a,b∈ \( Q \)

In the first case, we obtain

10 = a² −b,

a²b = −1,

solving for which gives us b² + 10b + 1 = 0, from which we can see that b is not rational. Likewise, in the second case we find that

b² = 1,

a² − 2b = 10,

and a is not rational, meaning \( f(x) \) is irreducible.

For factorization modulo p, we first complete the square;

\( f(x)={({x^{2}}-5)^{2}}-24 \)

we now focus on the square root of 24, which is 2 \( \sqrt[]{6} \) . We write this as 2m, where m is the integer such that m² \( ≅ \) 6 mod p: for p such that m is solvable, \( f(x) \) can be factorized as (x² − 5 + 2m)(x ² − 5 − 2m).

For p such that m has no solution in \( Z \) p, we try the next approach and try to find an element \( j+km \) in the field extension \( Z \) p[m] such that 5+2m = (j+km)². Lining up the coefficients gives us

j² + 6k² = 5,

jk=1.

From this we note that k = j⁻¹, and that the resultant equation

j⁴ − 5j² + 6 → (j² −2)(j² − 3),

must have a solution, for if

\( (\frac{2}{p})=(\frac{3}{p})=-1 \)

then \( (\frac{6}{p})=1 \) . We notice that, since (j + j⁻¹m)² = 5 + 2m, (j −j⁻¹m)² =5 − 2m, and we write (x² − 5 + 2m)(x ² − 5 − 2m) as

(x² − (j −j⁻¹m)²)(x ² − (j + j⁻¹m)²)

→ ((x−j) + j⁻¹m)((x + j) − j⁻¹m)((x −j) − j⁻¹m)((x + j) + j⁻¹m)

→ ((x−j) + j⁻¹m)((x −j) − j⁻¹m)((x + j) + j⁻¹m)((x + j) − j⁻¹m)

→ ((x−j)² − 6j⁻¹)((x + j)² − 6j⁻¹)

and we are done.

Theorem 2.6 (Dedekind) Let f(x) be a polynomial over \( Z \) [x] with Galois group G and a factorization modulo some prime p

\( f(x)=\prod _{i=1}^{j}{h_{i}}(x) mod p \)

where each h_i(x) is a distinct, irreducible, monic factor such that

\( \sum _{i=1}^{j}deg⁡({h_{i}})=deg⁡(f) \)

Then G must contain a cycle of type:

(deg(h₁),deg(h₂),...,deg(h_j))

Remark 2.7 An irreducible quartic polynomial is hollow if and only if it has the Galois groups V₄ or A₄

Proof 2.4 It follows from Dedekind’s Theorem (2.6) that a polynomial of degree n has an n-cycle in its Galois group if and only if it is irreducible for some prime p. This means we can say that an irreducible polynomial is reducible modulo every prime p if and only if it has no n-cycle in its Galois group. However, a polynomial with a Galois group that is not transitive in S_n must be reducible([6], Theorem 2.9, pg.3). In the case of quartic polynomials, the only transitive subgroups of S₄ that satisfy this condition are V₄ and A₄.

3 Biquadratic polynomials and the V₄ group

3.1 Irreducible polynomials with Galois group V₄

In the following section we will consider hollow polynomials with Galois group V₄.

Definition 3.1 Define the minimal polynomial a( \( x \) ) of α ∈ E/F for some Galois extension E/F as the unique, irreducible monic polynomial with Galois group

Gal(E/F). This is given by

\( α(x)=\prod _{σ∈Gal(E/F)}(x-σ(α)) \)

when the stabilizer group of the Galois action Stab(α) = 1. Alternately, we define the minimal polynomial of α as

\( α(x)=\prod _{σ∈G/S}(x-σ(α)) \)

where G = Gal(E/F) and S = Stab(α)

Example 3.2 Find the minimal polynomial of the element α = 5 \( \sqrt[]{6} \) in the extension E/F = \( Q \) ( \( \sqrt[]{2} \) , \( \sqrt[]{3} \) ). We have \( Q \) ( \( \sqrt[]{2} \) , \( \sqrt[]{3} \) ) = \( Q \) ( \( \sqrt[]{2} \) ) × \( Q \) ( \( \sqrt[]{3} \) )), so Gal(E/F) \( ≅ \) V₄.

Examining the Galois action δ(α), δ∈ Gal(E/F), we see that |Stab(α) = 2| and Orb(α) = {α,−α}. The minimal polynomial is then given by

a( \( x \) ) = ( \( x \) − 5 \( \sqrt[]{6} \) )( \( x \) + 5 \( \sqrt[]{6} \) ) = \( x \) ² − 150.

As we can see, although α is an element of E/F where Gal(E/F) \( ≅ \) V₄, its minimal polynomial is not quartic and therefore does not have Galois group V₄. We gather that the degree of the minimal extension is determined by the cardinality of its stabilizer group and that an element α in E/F has Galois group equal to Gal(E/F)if and only if it has a trivial stabilizer group under the action of the group Gal(E/F). In other words, it holds if α is not fixed by any non-trivial automorphism of E/F.

We now consider when Gal(E/F) \( ≅ \) V₄:

Lemma 3.3 The Galois extension E/F = \( Q(\sqrt[]{j} \) , \( \sqrt[]{k} \) ) is equivalent to \( Q \) ( \( \sqrt[]{j} \) + \( \sqrt[]{k} \) )

Proof 3.1 Define j and k as distinct, square-free j,k̸ \( ∉Q \) ) Let G = Gal(E/F); it can be shown that G \( ≅ \) V₄. Let K denote the intermediate field F ⊂ K ⊂E generated by \( \sqrt[]{j} \) + \( \sqrt[]{k} \) . Then the Galois group of the extension E/K is, by definition, the group of automorphisms of E/K fixing K. Since E^FK, Gal(E/K)(E/F). We see that since the three non-trivial elements of Gal(E/F) respectively fix \( \sqrt[]{j} \) , \( \sqrt[]{k} \) , and \( \sqrt[]{jk} \) , no element fixes \( \sqrt[]{j} \) + \( \sqrt[]{k} \) . Therefore |Gal(E/K)| = |Aut(E/K)| = 1. By the Fundamental Theorem of Galois Theory, we have

\( {E^{Gal(E/F)}}=K→E=K \)

It follows that \( \sqrt[]{j} \) + \( \sqrt[]{k} \) is a primitive element of E/F, so, as desired, \( Q \) ( \( \sqrt[]{j} \) , \( \sqrt[]{k} \) ) \( ≅ Q \) ( \( \sqrt[]{j} \) + \( \sqrt[]{k} \) ).

Corollary 3.4 We can express an element in the extension generated by \( \sqrt[]{j} \) + \( \sqrt[]{k} \) as \( a\sqrt[]{j} \) + \( b\sqrt[]{k} \) , where j and k are distinct square free integers, not necessarily

positive, and a,b∈ \( Q \) .

Remark 3.5 We further apply the argument presented in Lemma 3.3 to elements in E/F of the form l+ \( \sqrt[]{j} \) + \( \sqrt[]{k} \) + \( \sqrt[]{jk} \) , and show that this too is a primitive element of E/F. Note that the dimension of the extension is 4, also the number of basis vectors in this element. It follows that every element in the extension E/F where Gal(E/F) \( ≅ \) V₄ can be written in the form a + \( b\sqrt[]{j} \) + \( c\sqrt[]{k} \) + \( d\sqrt[]{jk} \) , where a,b,c,d∈ \( Q \) . The same condition from Corollary 3.4 applies for j,k, and jk. Noting that we do not necessarily need jkto be square free, as that would restrict j and k to be co-prime.

We are now able to use this result to find the V₄-generic class of irreducible polynomials.

Theorem 3.6 If a polynomial is irreducible over Q and has Galois group V₄, then it can be written in the form

\( \prod _{σ∈G/S}(x-σ(a+b\sqrt[]{j}+c\sqrt[]{k}+d\sqrt[]{jk})) \)

or, written out,

\( (x-(a+b\sqrt[]{j}+c\sqrt[]{k}+d\sqrt[]{jk}))(x-(a+b\sqrt[]{j}-c\sqrt[]{k}-d\sqrt[]{jk})) \)

\( (x-(a-b\sqrt[]{j}+c\sqrt[]{k}-d\sqrt[]{jk}))(x-(a-b\sqrt[]{j}-c\sqrt[]{k}+d\sqrt[]{jk})) \)

We will not provide the fully expanded form due to its being too intricate, but it can be shown that the coefficient of the \( {x^{3}} \) term is −4a. By setting a to 0, we instead consider all reduced quartic polynomials, and have removed one parameter from the expression, giving

\( (x-(b\sqrt[]{j}+c\sqrt[]{k}+d\sqrt[]{jk}))(x-(b\sqrt[]{j}-c\sqrt[]{k}-d\sqrt[]{jk})) \)

\( (x-(-b\sqrt[]{j}+c\sqrt[]{k}-d\sqrt[]{jk}))(x-(-b\sqrt[]{j}-c\sqrt[]{k}+d\sqrt[]{jk})) \)

This, too, cannot be easily manipulated. In the next theorem, we shall only consider two parameters.

Definition 3.7 Define a quartic polynomial to be ”biquadratic” if it can be written as

\( {x^{4}} \) + a \( {x^{2}} \) + b

for some a,b∈ \( Q \) .

Theorem 3.8 A biquadratic polynomial p(x) is irreducible in Q and has Galois group V₄ if and if only if it can be written in the form

\( {x^{4}}-2(u+v){x^{2}}+{(u-v)^{2}} \) (3.1)

where u and v are distinct rationals such that none of u, v or uvcan be written as a ratio of two squares.

Proof 3.2 Let us set one of b,c, or d to 0. There are now no simpler polynomials that we can construct, as removing any more parameters will result in a non-trivial stabilizer group. We now have either

\( α=\sqrt[]{{b^{2}}j}+\sqrt[]{{c^{2}}k}, \)

\( α=\sqrt[]{{c^{2}}k}+\sqrt[]{{d^{2}}jk}, \)

Or

\( α=\sqrt[]{{b^{2}}j}+\sqrt[]{{d^{2}}jk} \)

Without loss of generality, we can write any three of these as

\( α=\sqrt[]{u}+\sqrt[]{v} \)

with distinct u,v ∈ \( Q \) . We must further restrict u and v in a way that is equivalent to the conditions given in 3.4 and 3.5. It must hold that neither \( \sqrt[]{u} \) or \( \sqrt[]{v} \) are in \( Q \) . We must further restrict u and v such that \( \sqrt[]{u}+\sqrt[]{v} \) cannot be written as a single radical, in which case Stab(α) = 2, so we end up with the conditions u,v, and uv cannot be written as ratio of two square integers. From this, the computation of the orbit group of Gal(E/F) on α should follow easily, and we find the minimal polynomial of α to be

\( a(x)=(x-\sqrt[]{u}-\sqrt[]{v})(x+\sqrt[]{u}+\sqrt[]{v})(x-\sqrt[]{u}+\sqrt[]{v})(x+\sqrt[]{u}-\sqrt[]{v}) \)

Which we write as

\( a(x)=({x^{2}}-{(\sqrt[]{u}+\sqrt[]{v})^{2}})({x^{2}}-{(\sqrt[]{u}-\sqrt[]{v})^{2}})， \)

And finally as

\( a(x)={x^{4}}-2（u+v）{x^{2}}+{(u-v)^{2}}， \)

Corollary 3.9 Since there are no other ways to construct a minimal polynomial a(x) with the Galois group V₄ such that a(x) is of the form

\( {x^{4}}+a{x^{2}}+b， \)

we conclude that all irreducible polynomials of the form \( {x^{4}}+a{x^{2}}+b \) must also be of the form of equation (3.1)

Corollary 3.10 All hollow polynomials of the form \( {x^{4}}+a{x^{2}}+b \) can be written as equation (3.1)

3.2 Biquadratic Polynomials Modulo p

We have found an exclusive family of irreducible biquadratic polynomials which contains all hollow polynomials for V₄. We now attempt to find an exclusive family of hollow polynomials for V₄; we do this by first generalizing the argument to all biquadratic polynomials, and considering the conditions under which they are reducible modulo p.

Theorem 3.11 A biquadratic polynomial

\( f(x)={x^{4}}+α{x^{2}}+β \)

is irreducible in \( Q \) but reducible mod p for every prime p if and only if

α² − 4β \( ≠ \) □, β = □, 2 \( \sqrt[]{β} \) −α \( ≠ \) □, −2 \( \sqrt[]{β} \) −α \( ≠ \) □

where □ indicates a perfect square number.

Remark 3.12 Let us take the minimal biquadratic polynomial of V₄,

\( a(x)={x^{4}}-2（u+v）{x^{2}}+{(u-v)^{2}}， \)

with the same constraints on u and v and with the added condition that 2(u + v),(u −v) ∈ \( Z \) and examine it using the criteria above:

(−2(u + v))² − 4(u −v)² = 16uv,

which by our hypothesis is not a square.

(u −v)² = □ always holds, of course, and

\( 2\sqrt[]{{(u-v)^{2}}}-(-2(u+v))=4u \)

\( -2\sqrt[]{{(u-v)^{2}}}-(-2(u+v))=-4v \)

both of which are by hypothesis not squares.

Since we have shown that all biquadratic hollow polynomials must be of the form

\( a(x)={x^{4}}-2（u+v）{x^{2}}+{(u-v)^{2}}， \)

then it follows that polynomials that all biquadratic polynomials of the form

\( a(x)={x^{4}}-2（u+v）{x^{2}}+{(u-v)^{2}}， \)

2(u + v),(u −v) ∈ \( Z \)

must be hollow.

Example 3.13 Consider x⁴ +1, which we have previously shown to be hollow. By lining up the coefficients, we have

u + v = 0

|u −v| = 1,

and we conclude that x⁴ + 1 is the minimal polynomial of \( \frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i \)

3.3 Biquadratic Polynomials Modulo n

Up until now, we have dealt with polynomials that are hollow in p, but it turns out that there exist polynomials that are hollow in every integer n greater than 1.

Example 3.14 The polynomial \( f(x)={x^{4}}-72{x^{2}}+4 \) is irreducible over \( Q \) but reducible modulo every integer n >1. To show that \( f(x) \) is irreducible over \( Q \) , we consider

f(x + 1) = (x⁴ + 4x³ + 6x² + 4x + 1) − 72(x² + 2x + 1) + 1

→ x⁴ + 4x³ − 66x² − 140x − 71,

which is irreducible by Eisenstein’s criterion ([10], p.12). Additionally, we can see that f(x) is hollow in p, by Theorem 3.11. We will use the following theorem to complete our proof for this claim.

Theorem 3.15 A polynomial of the form

f(x) = x⁴ − 2(s₁ + s₂)x² + (s₁ −s₂)²

is irreducible over Z but reducible modulo n for every integer n greater than 1 if s₁ and s₂ are distinct odd primes that satisfy

\( {s_{1}}≡1(mod 8)，(\frac{{s_{2}}}{{s_{1}}})=1 \)

Proof 3.3 In order to prove the hollowness for n, we need to prove that f(x) is reducible modulo p^k for each arbitrary positive integer k. We first define t = s₁ −s₂. Then we can easily find that

α² − 4t² = 16s₁s₂ \( ≠ \) □, −α + 2t = 4s₁ \( ≠ \) □, −α − 2t = 4s₂ \( ≠ \) □

Because s₁ ≡ 1 (mod 8), −α+2t modulo 2^k can only be a square. As \( (\frac{{s_{2}}}{{s_{1}}})=1 \)

−α − 2t is a square modulo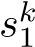. By the law of quadratic reciprocity

\( (\frac{{s_{1}}}{{s_{2}}})(\frac{{s_{2}}}{{s_{1}}})={(-1)^{\frac{{s_{1}}-1}{2} \frac{{s_{2}}-1}{2}}} \)

we can get \( (\frac{{s_{2}}}{{s_{1}}})=1 \) and −α − 2t modulo 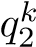is a square. If \( (\frac{{s_{α}}}{p})=1 \) (where a = 1 or 2), then −α±2t is a square modulo p^k. While if \( (\frac{{s_{α}}}{p})=-1 \) , then \( (\frac{{s_{1}}{s_{2}}}{p})=1 \) and α² − 4t² modulo p^k is a square. Therefore, f(x) is hollow for p^k. Since every integer greater than 1 can be factorized into a form of 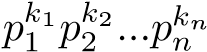and’s are co-prime, we can use Chinese Remainder Theorem[11] to get lemma 3.16

Lemma 3.16 If f(x) is reducible modulo all p^k for all prime p, then it’s reducible modulo n for all n.

Therefore, we can easily end the proof.

Remark 3.17 We notice the similarity between the respective expressions for biquadratic polynomials hollow in p and in n. The reader can check that the smallest pair of primes satisfying Theorem 3.15 are 2 and 17, the corresponding polynomial of which is x⁴ − 38x² + 225. The next smallest pair of primes of primes are 13 and 17, which gives x⁴ −60x² +16, the third smallest, 17 and 19, gives us the polynomial considered in Example 3.14.