1.  Introduction

Microorganisms such as bacteria have evolved sophisticated mechanisms to swim efficiently in highly viscous fluid environments, where the effects of inertia are negligible and movement is governed entirely by viscous forces. One of the most well-known strategies is the use of helical flagella: flexible, whip-like appendages that rotate to generate propulsion [1]. At such low Reynolds numbers, traditional locomotion strategies fail, and non-reciprocal motions—such as helical rotation—are required to achieve net displacement, as explained by Purcell's scallop theorem.

However, direct observation and manipulation of real bacteria present significant challenges due to their microscopic scale and sensitivity to environmental disturbances. To address this, our study proposes a biomimetic approach by constructing a scaled-up swimmer model that replicates the geometric and dynamic properties of bacterial propulsion. This macroscopic analog allows for easier fabrication, observation, and quantitative analysis while preserving the essential physics of low Reynolds number swimming.

The motivation behind this project is twofold: to provide a platform for validating theoretical fluid dynamics models such as resistive force theory (RFT), and to offer an accessible educational tool that bridges biological insight and mechanical implementation [2]. By recreating bacterial swimming behavior in a controllable, observable setup, we can gain deeper understanding of the fundamental principles that govern motion in viscous media, and apply this knowledge in soft robotics, microfluidics, and bioengineering contexts.

2.  Theory and methods

2.1.  Theoretical background

The theoretical foundation of this study integrates three core frameworks: Purcell’s scallop theorem, resistive force theory (RFT), and Buckingham Pi dimensional analysis. Purcell’s scallop theorem states that at low Reynolds number, reciprocal motion cannot generate net propulsion due to the time-reversible nature of the governing Stokes equations. This principle necessitates the use of non-reciprocal mechanisms such as helical rotation for effective locomotion [3]. Building upon this, resistive force theory models the propulsion generated by a rotating helical flagellum through the balance of anisotropic viscous forces. In our approach, the local viscous force acting on a small segment of the flagellum is expressed as a combination of normal and tangential drag components, using coefficients adjusted from Magariyama and Kudo’s extensions to account for helical structure and polymer resistance in solution [2]. Furthermore, in order to construct a scaled model that preserves the fundamental dynamics of bacterial swimming, dimensional analysis was applied using the Buckingham Pi theorem. A scale factor of 25,000 was employed to enlarge the dimensions of the swimmer while targeting a Reynolds number below 0.1, which was achieved by introducing a high-viscosity medium such as a detergent solution. These theoretical principles guided both the derivation of swimmer velocity from angular rotation and the selection of geometric and environmental parameters during simulation and fabrication, ensuring consistency between microscale theory and macroscale implementation [4].

2.2.  Research method

The swimmer was first modeled using CATIA software, where its body and helical tail were designed to replicate the geometry of bacterial flagella, as shown in Figure 1. Multiple test prints were conducted using different materials including ABS, PETG, and PLA. After evaluating the mechanical properties and print precision, PLA was ultimately chosen due to its excellent stiffness-to-weight ratio, ease of printing, and good water resistance, which made it especially suitable for underwater experimentation [5,6].

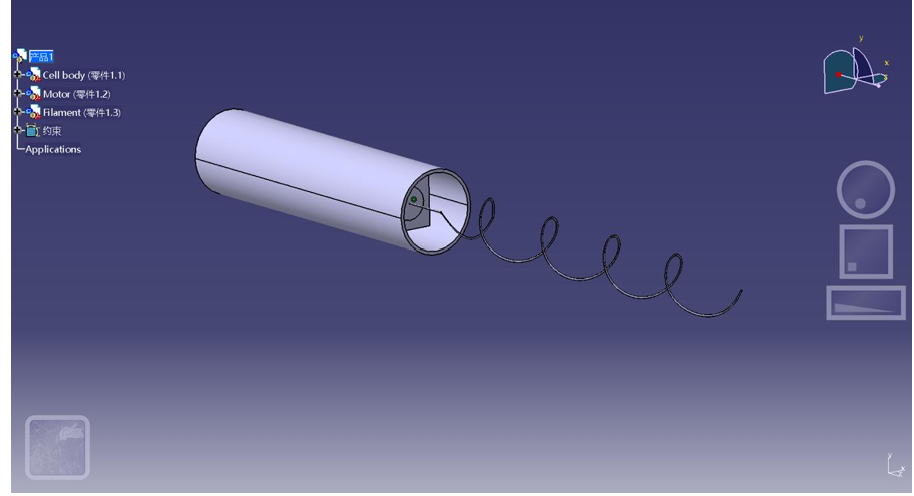
To simulate bacterial flagellar propulsion without using electronic components, this experiment designed a simple elastic drive mechanism: a rubber band was manually twisted to store elastic energy, which was then released to rotate the flagellum of the swimmer and propel it forward. This method provided a stable torque source and achieved a rotational frequency of approximately 2 Hz. The complete motion process of the swimmer in both water and detergent solution was recorded using a slow-motion camera setup, serving as the basis for analyzing its displacement and angular motion.

2.3.  Data processing

To ensure the reliability of the experimental results, each condition—whether in water or in detergent solution—was subjected to ten independent trials. From these, five datasets showing the highest consistency were selected based on multiple criteria, including the degree of visual overlap in the swimmer's trajectories and minimal variation in measured values. The angular velocity and linear speed from each selected dataset were then averaged to generate representative data, as shown in Table 1 and Table 2, which are presented in the results section for further analysis. These values form the basis for the regression and performance comparisons discussed in later sections.

2.4.  Statistic methods

To evaluate the relationship between angular velocity and translational speed, linear regression analysis was performed in MATLAB. The average angular velocities and corresponding translational velocities were entered as x and y vectors respectively. The polyfit function was used to compute a first-order polynomial regression model, representing the linear relationship between angular speed and swimming velocity. The resulting polynomial coefficients were then evaluated using the polyval function to obtain fitted values for comparison with experimental data. The fitted results were plotted together with the original data points using the plot function to assess consistency. The code is provided in the appendix [7,8].

3.  Results and analysis

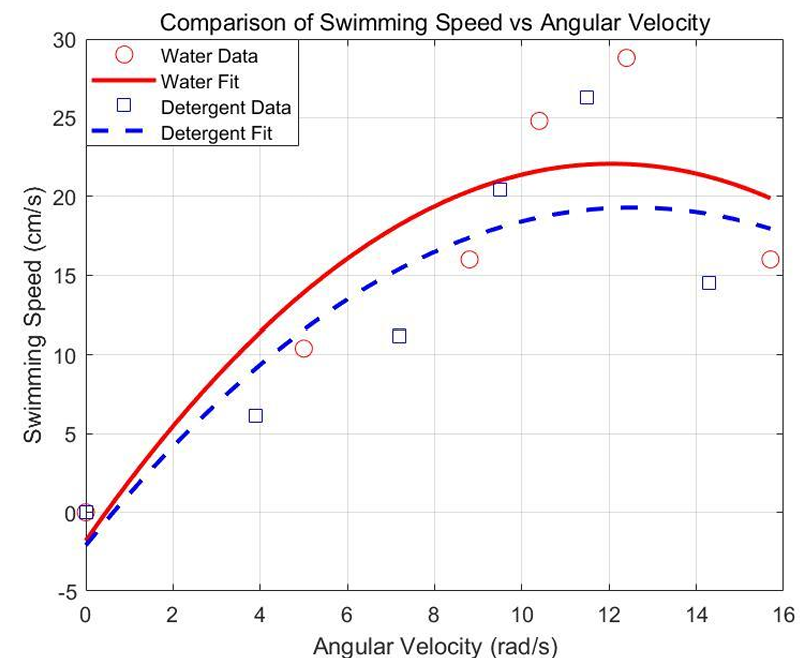
In Figure 2, the results reveal distinct motion characteristics of the flagellated swimmer in water and detergent solution, clearly captured in the comparison plot. In both fluids, swimming speed rises initially with increasing angular velocity, peaking around 12–13 rad/s, and subsequently declines. This non-monotonic trend is consistent with prior observations in low Reynolds number propulsion, where drag anisotropy and torque-speed imbalance limit propulsion beyond an optimal frequency [9].

In water, the swimmer reaches a maximum average speed of 28.8 cm/s at 12.4 rad/s. At lower speeds (under 10 rad/s), propulsion efficiency is visibly reduced, while at higher frequencies above 13 rad/s, the swimmer likely encounters excess drag or unsteady propulsion. In detergent solution, the same pattern occurs with slightly lower magnitudes: maximum velocity is about 26.3 cm/s at 11.5 rad/s. The shift in peak and reduction in performance indicate the effect of increased viscosity, which dampens rotational-to-translational efficiency [10].

Regression analysis further quantifies these effects. The fitted curves—second-order polynomials—indicate strong correlation between angular velocity and swimming speed, with coefficients of determination R² near 0.99 in both cases. The red solid curve represents water data, which not only peaks higher but shows steeper initial growth. The blue dashed curve shows a more subdued response in detergent, reflecting energy loss in overcoming greater fluid resistance.

This graphical and statistical analysis together highlight that although angular velocity is the driver of propulsion, fluid viscosity fundamentally shapes the swimmer’s efficiency and speed profile. The nonlinear nature of the curves emphasizes the need for tuning operational frequency to match fluid properties for optimal swimming performance.

4.  Discussion

The propulsion behavior exhibited by the swimmer under low Reynolds number conditions aligns closely with theoretical expectations. In water, the relatively low viscosity reduces hydrodynamic resistance, enabling the swimmer to achieve higher translational speeds for a given angular velocity. In contrast, the detergent solution—due to its higher viscosity—introduces greater resistance forces acting on the swimmer, thereby diminishing propulsion efficiency despite similar rotational input. This viscosity-induced effect is clearly reflected in both the regression curves and the observed peak velocities.

Nonetheless, certain deviations in the data can be attributed to various experimental uncertainties. These include potential measurement inaccuracies, limitations in camera frame rate, and minor inconsistencies inherent to the elastic driving mechanism. Additionally, due to fabrication constraints and lack of precise control, the swimmer occasionally exhibited non-linear trajectories or slight wobbling during motion, which introduced minor discrepancies from predicted velocity values.

Despite these challenges, the study demonstrates substantial value as a physical analog for microscale swimming behavior, offering a practical and accessible platform for exploring low Reynolds number fluid dynamics. This approach also holds significant promise for educational demonstrations, allowing students and researchers to visualize and test theoretical models in a tangible, macro-scale format. Moreover, it provides an effective means of validating numerical simulations and resistive-force-based propulsion theories.

Looking forward, future work could focus on refining the actuation mechanism by integrating precision-controlled electric motors, which would enable better frequency tuning and improved repeatability. Furthermore, incorporating flow visualization techniques—such as particle image velocimetry (PIV)—would allow for more detailed insight into the interactions between the swimmer and its surrounding fluid. Expanding the research to include other non-Newtonian fluids or exploring artificial cilia-based propulsion systems could further enhance our understanding of microswimmer dynamics and open pathways toward real-world applications, such as targeted drug delivery, bio-robotics, and microfluidic transport systems.