1.  Introduction

Black holes are cosmic structures that formed after the gravitational implosion of baryonic or dark matter. Under certain circumstances, black holes may merge, forming supermassive black holes (SMBHs), whose masses range from  $$ {10}^6$$  to  $$ {10}^{10}$$  solar masses. SMBHs observed today are found in the centers of galaxies, as they once served as the dominant source of gravity that bound baryonic and dark matter together to form galaxies. Yet SMBHs are not the sole contributor to galactic evolution.

Dark matter halos have played major roles both in shaping the timeline of the birth of cosmic structures and determining galactical structure after galaxy formation. In section 2, this paper will investigate how the masses of dark matter halos at the center of galaxies effect the growth of galactic SMBHs, and how SMBHs of different growth rates differ in feedback, which would influence how baryonic matter is heated or expelled in galaxies. The heating and expelling poses major influence on gas inflow rate, star formation and the development of galactic structures such as the bulge, disk and spiral arms.

Section 3 will discuss how different dark matter models, namely hot, cold, warm and lamda cold dark matter effect the timeline of the development of cosmic structures. Different dark matter models produce various transfer functions, where each function can be used to infer the matter power spectra, a parameter that can be used to measure whether the dark matter model erases density fluctuations that are existent at the beginning of the universe, which in turn determines the sequence and timing of galaxy formation. In this section, this paper will introduce basic properties of each dark matter model, identify their respective transfer functions, then explain what implications the varying transfer functions pose for galactic structure evolution.

In section 4, this paper will present a graphical comparison of the matter power spectra predicted by the dark matter models mentioned in section 3. By demonstrating the matter power spectra differences under identical comoving wave numbers, this graph would help to visualize how the timeline of cosmic evolution diverges depending on the type of dark matter. This paper will then compare the predictions of each dark matter model to observational results, and identify the dark matter model that is most consistent with observations.

This paper examines how dark matter influences galaxies from two perspectives: galactical structure and cosmic evolution timeline. Not only does section 2 provide key insights into galactic evolution, section 3 proposes a novel way of comparing the competence to smooth out density fluctuations of each type of dark matter by using the transfer functions, whereas the graphical comparison featuring the matter power spectra derived using transfer functions also adds in new key evidence on which dark matter theory corresponds the best with observational results. Hopefully this paper would be useful to future research aimed at studying cosmic evolution and dark matter.

2. Galactic structures

2.1. Gas inflow rate

The virial radius is the radius of a region where a gravitational system is in gravitational equilibrium, and virial velocity is the typical rotation speed of matter within this system. Together they decide the value of the potential depth of a dark matter halo, which a measure of how strongly matter is trapped by a dark matter halo’s gravity, as the depth is represented by the virial velocity at the virial radius. The relation between virial velocity and virial radius is shown through this equation [1]:

$$ V_{vir}=\sqrt{\frac{GM}{R_{vir}}}$$(1)

Following the idea of the two-stage galaxy formation model proposed by White & Rees, the halo potential is highly influential to cooling times and gas inflow rates toward the halo center. The baryonic inflow rate, which supports both star formation and SMBH accretion is defined through the following equation:

$$ M_{inflow}\propto f_b\frac{M_{halo}}{t_{dyn}}$$(2)

, where  $$ f_b$$  is the baryon fraction and  $$ t_{dyn}$$  is​ the dynamical time. This directly links halo mass to SMBH feeding rate. SMBH growth is rapid when fed baryonic matter through cooling gas flows or merger driven inflows fueled by massive dark matter holes. In contrast, low mass halos lack sufficient potential wells to attract sufficient gas inflow for rapid SMBH growth.

2.2. Galactic structures

Massive dark matter halos mean that the SMBH fed by the gas inflow it supported accrete and grow at a rapid pace. Once the SMBH become supermassive, it projects enormous energy back into the galaxy through active galactic nucleus (AGN) feedback. This feedback heats and expels gas, stopping new stars from forming in the central region. Over time, the galaxy becomes an elliptical system with a large bulge and seldom star formation. In smaller halos, SMBHs stay small because gas flows less efficiently to the center. These galaxies keep forming stars in their bulges for billions of years, resulting in smaller bulges and disk-dominated structures.

Disks are susceptible to turbulence. In low-mass halos, disks remain intact due to the inactive AGN feedback. Star formation continues, and the galaxy stays a spiral. In massive halos, SMBHs produce strong AGN feedback that can disturb or even destroy disks. As the heat of the projected gas prevents further cooling, most galaxies with massive dark matter halos are ellipticals without disks.

To form spiral arms, a cold, thin disk and steady gas supply are needed. For galaxies with low-mass dark matter halos where SMBHs are weak and the disk isn’t disrupted by feedback, the spiral structure is kept for billions of years. However, in massive halos, feedback heats the gas and stirs turbulence, which disrupts spiral arm structures. After multiple mergers, the disk is gone, and the galaxy becomes a featureless elliptical.

2.3. Star formation

The gas inflow rate is relevant in the form of star formation rate. Stars form more vigorously in environments with an abundant supply of cold gas and so that a potential trigger could start the collapsing progress. The star formation rate surface density is typically calculated by the Kennicutt–Schmidt law given below [2]:

$$ {\dot{\mathrm{\Sigma }}}_{*}=A{\mathrm{\Sigma }}_{gas}^n$$(3)

The equation states that star formation rate is significantly higher in regions where gas density is high. In galaxies with low-mass dark matter halos, gases are free from disruptions from strong AGN feedback exclusive to galaxies with massive dark matter halos, allowing the gas to form dense clouds that could collapse inward to form stars in the future.

Another important metric is the specific star formation rate (sSFR), which measures the star formation rate with the stellar mass as a variable instead of gas density:

$$ sSFR=\frac{SFR}{M_{*}}$$(4)

where SFR is the total star formation rate and  $$ M_{*}$$ ​ is the stellar mass. This relation depicted in the equation demonstrates the pace at which stars are formed depending on the size of the galaxy. According to the standard set by Goubert et al [3]., galaxies with an sSFR of lower than  $$ {10}^{-11}{yr}^{-1}$$  are considered quenched, meaning that they form too little stars relative to their stellar mass. Wetzel et al. have concluded [4], according to their analysis of SDSS DR7 data, that more massive central galaxies have a decreased likelihood of high sSFRs and an enhanced likelihood of low sSFRs. Hence dark matter influence galaxies in that the star formation rate decreases as halo mass increases.

3. Dark matter models

3.1. Background

Though most matter was evenly distributed in the early universe, small fluctuations existed, which can be observed today as temperature patterns in the cosmic microwave background (CMB) [5]. These fluctuations played a crucial role in the evolution of cosmological structures. The regions with larger densities grew due to gravitational forces, and were able to collapse into dark matter halos, influencing galactic evolution. However, whether these fluctuations survived being smoothed out during the early stages of the universe depended partially on the nature of dark matter.

The inflationary theory predicts a spectrum of initial perturbations, described by a primordial power spectrum [6]. Once generated, the primordial fluctuations evolved under the influence of gravity, cosmic expansion, and the properties of dark matter. How cosmic expansion impact the evolution of such fluctuations is studied by cosmologists through their analysis of how fluctuations of different comoving wavenumbers k respond to cosmic expansion, which came down to the Einstein–Boltzmann equations as a result. As for dark matter, the crucial factor is whether the particles are moving fast enough to smooth out fluctuations by free streaming or slow enough to allow gravitational amplification [7].

Free streaming describes the motion of particles traveling across density variations, smoothing out small-scale fluctuations in the meantime. For a particle with velocity v(t), the free-streaming length is given by:

$$ {\lambda }_{fs}\left(t\right)={\int }_0^t\frac{v\left(t^{\text{'}}\right)}{a\left(t^{\text{'}}\right)}d{t}^{\text{'}}$$(5)

Perturbations on scales smaller than  $$ {\lambda }_{fs}$$  are smoothed out, while larger fluctuations survive and can grow gravitationally.

One way to quantify whether perturbations are smoothed out is to use the transfer function, T(k), which demonstrates how the value of T(k) differs under different values of k, the comoving wave number, a measure of the size of cosmic fluctuations [8]. A large k represents small structures such as galaxies, while a small k can represent structures up to the scale of superclusters. Different values of T(k) represent different fates of the perturbations. A value of T(k)=1 means that fluctuations survive intact, while values below one means they are smoothed out. The behavior of T(k), and therefore whether early perturbations are smoothed out, depends heavily on the properties of dark matter particles.

3.2. Dark matter models

3.2.1. Hot dark matter

The hot dark matter (HDM) model predicts that the universe in filled with light, fast particles. Because these particles traveled at near-relativistic speeds, they could move across the universe and smooth out the density fluctuations by free streaming on large scales in a short time before gravity broadens the density fluctuations. According to the research of Bond, Szalay, and Turner (1982), The transfer function of HDM can be calculated with the following function [9]:

$$ T_{HDM}\left(k\right)=e^{-\frac{k}{k_{fs}}}$$(6)

, where  $$ k_{fs}$$  is the comoving wave number k under the effect of free streaming. At higher levels of k, the value of T(k) decreases exponentially. In other words, the faster a particle moves, the more efficiently it can eliminate density fluctuations before gravity has time to pull matter together. HDM predicts a scenario where density fluctuations are erased, and only very large structures like superclusters form first and galaxies appear much later by fragmentation.

3.2.2. Cold dark matter

In contrast with HDM, the cold dark matter (CDM) model is composed of heavy, slow-moving particles such as WIMPs or axions. These non-relativistic particles move little over time. Without rapid motion to erase fluctuations, small-scale density fluctuations remain intact, allowing gravity to amplify them. Bardeen, Bond, Kaiser, and Szalay solved the Einstein–Boltzmann equations for density perturbations in a CDM universe in their 1986 paper, and provided the following equation [10]:

$$ T_{CDM}\left(k\right)=\frac{1}{1+{\left(\frac{k}{k_c}\right)}^2}$$(7)

, where  $$ k_c$$ ​ marks the transition between large- and small-scale behavior. Unlike HDM, CDM retains a high value of T(k) at high k, signifying that small fluctuations could survive CDM contact, so galaxy-sized fluctuations can grow. This leads to a process where small halos collapse first, merge into galaxies, and eventually build larger systems like clusters and superclusters.

3.2.3. Warm dark matter

As suggested by its name, warm dark matter (WDM) possesses properties of both HDM and CDM. Its particles move fast enough to erase the small-scale fluctuations but not so fast as to eliminate galaxy-scale ones. How the T(k) of WDM changes according to the scale of fluctuations is enlisted below [11]:

$$ T_{WDM}\left(k\right)={(1+{\left(\alpha k\right)}^2)}^{-2}$$(8)

T(k) declines gradually as k increases, showing a gradual reduction of small-scale fluctuations, reducing the number of small halos while galaxy-scale halos are still able to form. In this model, early galaxy formation is somewhat delayed compared to CDM, but not erased entirely.

3.2.4. Λ cold dark matter

The last dark matter model to present is the ΛCDM model, which builds on CDM by adding a cosmological constant, dark energy. By taking dark energy into consideration, accelerated expansion during the late-time evolution of the universe is correctly modeled by the transfer function of ΛCDM. This effect can be represented by a function similar to that of CDM:

$$ T_{\mathrm{\Lambda }CDM}\left(\mathrm{k}\right)=\frac{1}{1+{\left(\frac{k}{k_{\mathrm{\Lambda }}}\right)}^2}$$(9)

According to the research of Efstathiou, Bond, and White [12], this formula captures how dark energy halts the growth of structure at late times. While ΛCDM allows galaxies to form early in fashion as CDM, it also suppresses the growth of very large-scale structures at late times, effectively freezing the cosmic web in its current form.

3.3. Matter power spectrum

All of these transfer functions feed into the matter power spectrum [10],

$$ P\left(k\right)=P_{prim}\left(k\right){T\left(k\right)}^2$$(10)

which describes the strength of fluctuations at different scales. If the power spectrum retains high values at large k, small-scale fluctuations survive, get amplified by gravity and collapse early, producing galaxies at high redshift, as suggested by the CDM and ΛCDM models. If power is erased at small scales, as in HDM, galaxies can only form late. WDM falls between these extremes, erasing only the tiniest structures and leading to fewer small galaxies but preserving the larger structures such as superclusters.

4. Methodology

4.1. Description

To investigate how different dark matter models affect the survival of primordial fluctuations. I made a graphic that compared the fluctuation strength of the HDM, CDM, WDM and ΛCDM models under different cosmic scales.

For visualization, I employed logarithmic axes to span several orders of magnitude in both comoving wavenumber k and power spectrum amplitude. The x-axis represents the comoving wavenumber, with small values corresponding to large physical scales and large values corresponding to small scales. The y-axis is the matter power spectrum derived from the transit functions of each dark matter model. By plotting the four models on the same graphic, I obtained a direct comparison of the growth and survival of fluctuations varies across different dark matter assumptions, ultimately influencing the timing of galaxy and cluster formation.

4.2. Results

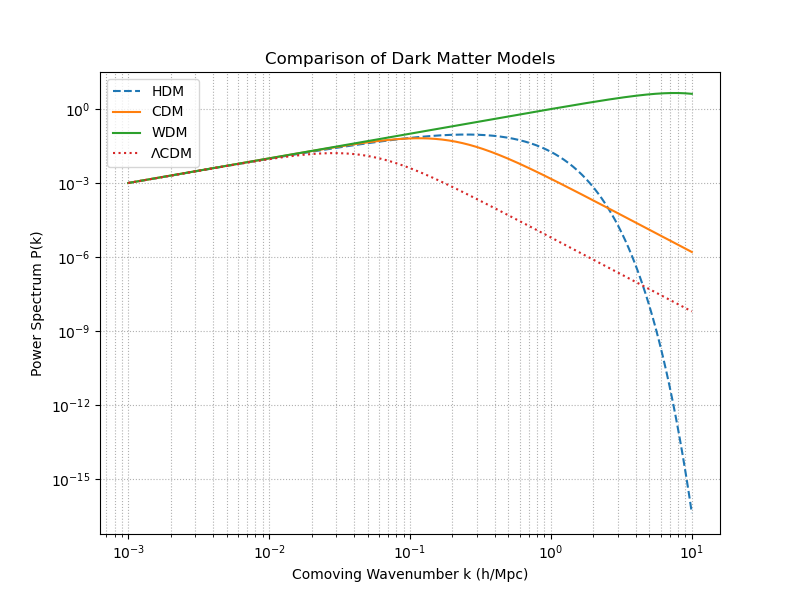
It can first be concluded from the graphic that the matter power spectrum is similar at large cosmic scales, but as k gradually increases, the survival state of fluctuation begins to vary due to different dark matter properties.

In the HDM case, its line representing the matter power spectrum falls off exponentially at high comoving wavenumbers, indicating strong suppression of small-scale fluctuations. Consequently, structure growth follows a process where large superclusters form first and fragment afterwards.

The CDM model shows very different behavior: fluctuation power is preserved across a wide range of scales, including small scales at large k. This enables the earliest collapse of small halos, which then merge into galaxies and clusters.

For WDM, the spectrum demonstrates a smooth but noticeable decline at high k, reflecting partial suppression of small-scale fluctuations. This feature reduces the number of very small halos, addressing some of the well-known issues of CDM, such as the overabundance of predicted dwarf galaxies. However, the model still retains sufficient small-scale power to form galaxies and clusters hierarchically.

Finally, the shape of the ΛCDM power spectrum line is nearly identical to that of CDM, especially at large scales. However, the two models began to differentiate at small scales, as the influence of dark energy introduces a suppression of growth, effectively halting the evolution of the largest structures in the late universe.

4.3. Discussion

The Sloan Digital Sky Survey (SDSS) has mapped millions of galaxies across a vast portion of the sky, producing a three-dimensional picture of the cosmic web [13]. On large scales, this web is relatively smooth, but on smaller scales, SDSS reveals abundant clustering. Galaxies grouped into clusters and superclusters. This observed distribution provides a direct test of dark matter models. HDM predicts a much smoother galaxy distribution, erasing small-scale clustering and delaying galaxy formation, which contradicts to what SDSS has observed. WDM produces partial suppression of small structures, but would predict fewer dwarf galaxies and reduced clustering strength compared to what SDSS observes. CDM, by contrast, naturally produces a bottom-up, hierarchical structure formation scenario that matches the filamentary cosmic web revealed by SDSS [13]. ΛCDM extends this success by including dark energy, which suppresses the growth of the largest structures at late times while preserving the small- and medium-scale clustering that SDSS detects. Thus, the qualitative picture from SDSS strongly favors CDM and ΛCDM, while ruling out HDM and tightly constraining WDM.

5. Conclusion

This paper has examined how dark matter shapes both galactic evolution and cosmic structure. The masses of dark matter halos decide gas inflows that fuel SMBHs, while SMBH feedback influences star formation and galactic structure. Large halo masses create larger black holes with more active feedback, which disrupt dense gas clouds, reducing star formation rate and promoting an elliptical galactic structure.

The survival of primordial density fluctuations depends on dark matter properties. HDM erases small-scale fluctuations, predicting a scenario without early galaxies which is inconsistent with observations. CDM preserves fluctuations, enabling hierarchical galaxy formation, while warm dark matter lies between these cold and hot dark matter. ΛCDM is built on CDM except for extra consideration of dark energy, which predicts a slower structural growth during late-time cosmic structure evolution.

Graphical comparisons of power spectra confirm that CDM and ΛCDM match SDSS observed galaxy distributions, while HDM and WDM fail. Thus, dark matter links particle physics to the architecture of the universe, with future discoveries expected from both particle searches and cosmological surveys.