1.  Introduction

Conditional probability—the cornerstone of probabilistic reasoning, enabling people to have a more comprehensive idea of uncertain events based on some evidence that they have previously found. It also forms the foundation of Bayesian inference, which is a well-known tool that is widely applied in artificial intelligence and medical diagnosis fields. However, everything has two sides; its application also has several challenges, especially when human cognition is involved in it. The Monty Hall Problem (MHP), also known as the three-door problem, serves as the foundation case study for this thesis to explore the strengths and limitations of conditional probability when facing real-world scenarios. In this classic puzzle, a contestant selects one of three doors, behind one of which lies a prize. After the host, who knows the location of the prize, opens a door without a prize aside from the contestant’s initial choice, the contestant must decide whether to stick with their first choice or switch. Probability theory indicates that switching doubles the winning probability from  $$ \frac{1}{3}\mathrm{ }$$ to  $$ \frac{2}{3}$$ , but human intuition often resists this logic, as some of them may still believe that the probability for the prize on each door remains constant at  $$ \frac{1}{3}$$ . This paper will utilize the MHP to evaluate the outstanding performance of conditional probability in different applications and its shortcomings under cognitive and situational conditions.

The counterintuitive nature of the MHP makes it a powerful tool for assessing human reasoning. Oaksford and Chater suggest that “people always use some everyday common probability strategies when dealing with some tasks, but due to their own cognitive biases, they often deviate from standard conditional probability [1].” Borhani and Green further note “the presence of exploring reasoning in MHP or similar situations, where biases such as over-reliance on initial choices lead to less optimistic outcomes [2].” Wilcox points out that the “possibility neglect bias—where individuals fail to adjust probabilities based on the likelihood of evidence—is also a key reason for errors in the MHP.” while Tubau emphasize “emotional biases such as the reluctance to change choices as a psychological behavior and sometimes cognitive illusions (e.g. assuming equal probabilities among remaining doors) may also contribute to errors [3,4].” These studies all reveal a critical limitation—even in a simplified environment like the MHP, human cognition may still be unable to truly internalize the meaning of conditional probability.

In contrast to some limitations, conditional probability also plays a key role in several real-world applications. Constantinou demonstrates “its powerful role in Bayesian artificial intelligence, where Bayesian networks can model uncertainty and optimize decisions in data-scarce situations, such as in risk management [5].” Tipping extends this idea to “the machine learning field, showing how Bayesian inference uses conditional probability to handle uncertainties and favour simpler models—an advantage stemming from its mathematical rigor [6].” Be more specific, Silva “apply it to assess risk dependencies in Brazil’s natural gas supply chain, identifying key vulnerabilities such as demand risk.” while Lindsey highlights “its role in medical diagnosis, updating probabilities based on his test results to address the complexity when doing diagnosis [7,8].”

However, its limitations become obvious when human factors or environmental noise intervene in the condition. Juslin “questioned its superiority, pointing out that in real-world environments with approximate data, simpler addition strategies might be even better than the results of probability theory due to cognitive constraints [9].” Morone and Adibpour further “emphasised this in an extended 10-door MHP, where the probability of winning by switching doors significantly increased (from  $$ \frac{1}{10}\mathrm{ }$$ to  $$ \frac{9}{10}$$ ), but biases such as status quo bias (emotional effect) still existed, and complexity did not guarantee better decision-making [10].”

From an educational perspective, the MHP offers a way to connect these two sides. Tubau, in his thesis, also proposed that “clear guidance on probability partitioning could eliminate cognitive illusions,” while Wilcox claimed, “support the use of mental simulation methods to reduce possibility neglect and enhance Bayesian reasoning [3,4].”

2.  Literature review

The Monty Hall Problem (MHP) is a classic probability problem that shows how altering the door from the earlier choice can raise chances of winning from  $$ \frac{1}{3}$$  to  $$ \frac{2}{3}$$. It is the main way to test the theoretical strengths and practical weaknesses of conditional probability. Originally, the rule of the MHP is “After people have made their choice, the host opens another door, revealing the outcome of it.” Based on this, people come up the idea that the conditional probability of winning by switching is…, establishing conditional probability’s role in updating beliefs based on new evidence. With some basic knowledge of probability, it’s easy to find that “The chances are 2 in 3 that the door initially chosen doesn’t hide a prize …switching certainly does give the prize,” which emphasising the counterintuitive nature of the problem. Gill, R. (n.d.) provides a mathematical analysis, explaining, “The key to accepting and understanding the paradox is to realise that the (subjective) probabilities relevant for the decision…depend on what is known about the development that led to this situation,” emphasizing the strength of conditional probability when modelling dependencies but also several limitations when assumptions like host neutrality are violated [11].

Real-world applications also demonstrate some strengths of conditional probability. Tipping, M.E. explains, “The first key element of the Bayesian inference paradigm is to treat parameters like  $$ \mathrm{w}$$ …as random variables the same as A or B, so it turns out that:

$$ f\left(A;w\right)=P\left(B\right|A)$$(1)

showing how conditional probability manages uncertainty in machine learning [6].” Constantinou, A.C. states, “Bayesian Networks (BNs) offer a framework for modelling relationships… suitable for modelling real-world situations where people seek to simulate the impact of various interventions,” applying conditional probability to optimise decisions in supply chains and forensics [5]. Silva, L.M.F. report, “The ANP indicated that the most critical risk in the links is the demand risk… with probability of 10%,” using conditional probability and simulations for supply chain risk assessment [7]. Lindley, D.V. notes, “People need to measure this confidence … in terms of probability… if they say the probability that the patient has hepatitis is, illustrating diagnostic updates with test results [8].” Miller, J.B., and Sanjurjo, A. connect the MHP to the economic field, stating that “The Monty Hall problem… known for its ability to confound the intuition…roughly 80-90 percent of subjects incorrectly stay with the same door.” applying restricted choice principles [12]. Borsetto, D. observes that “more than 50% of patients with Head-and-Neck Squamous Cell Carcinoma (HNSCC) experience loco-regional recurrence [13].”

However, for MHP, it has another factor that may have affected the participant’s choice—cognitive bias and mental state when they are facing that choice. In simple terms, it means that people are not always aware of the theoretical possibility when they must choose which to believe and support their choices. People always rely on their own beliefs more than theoretical results, and when they have to make a choice without time to think about it, they may always give up thinking rationally and just rely on the experience accumulated in their past lives, but usually, those thoughts are always limited and lack support.

To estimate VaR and CVaR with conditional probability, Martin, J. suggested the “informative prior Bayesian (IPB) method employs the existing relations between the parameters of the loss distribution and the parameters of the GPD [14].” Additionally, he also stated “cause and effect relationships among risks must be identified,” pointing out interdependencies that are often overlooked and “It is necessary to develop risk management models for real cases [14].” The following methodology is guided by these suggestions.

3.  Methodology

After a detailed review of the strengths and limitations of conditional probability, with the MHP as a case study, the review has been ensured to be rigorous, following PRISMA guidelines. Searches on Google Scholar and JSTOR using keywords: “conditional probability Monty Hall,” “cognitive biases MHD,” “Bayesian inference applications,” and “probability education.” Publications from 1975 to 2025 were targeted, selecting about 35 sources, with 17 finally chosen for relevance to theoretical foundations, cognitive biases, applications, and evaluations.

The criteria of inclusion prioritized peer-reviewed articles, books, or proceedings addressing conditional probability’s role in the MHP, real-world applications (e.g., Medicine, AI), or educational strategies. Non-peer-reviewed works or those lacking theoretical depth or irrelevant are excluded. Papers were categorized into several groups: theoretical frameworks, such as Bayesian models by Gill. N.D., cognitive limitations like Saenen, applications like Silva. [7,11,15].

Empirical validation used Monte Carlo simulations in Python, replicating the MHP (1000 trials) to confirm switching probabilities, as “the conditional probability of winning by switching is$$ \frac{2}{3}$$ [11].” A 10-door variant was also tested, following Morone, A. And Adibpour, N., to assess complexity effects [10]. Bias simulations modelled equiprobability in Saenen and likelihood neglect in Wilcox J.E. [3,15]. Case studies from medicine (by Lindley, D.V.), supply chains (by Silva, L.M.F.), and medical risk assessment (by Sethi, M.&Borsetto, D.) were analysed for dependency modelling via Bayesian theorem [7,8,16]. Financial risk simulation in Martin, J., noting that “IPB method employs the existing relations between the parameters of the loss distribution and the parameters of the GPD [14].” Additive integration was tested by Juslin, P. [9]. This approach ensures a direct evaluation of the conditional probability’s utility and barriers.

4.  Results

Theoretical Results: MHP simulations “replicated by Selvin, S., confirming the conditional probability of winning by switching is with arithmetic calculations showing a 66.7% win rate for switching.” from Gill, R. [11]. From Mill, J. B. “By Vos Savant, M., the chances are 2 in 3 that the door initially chosen hides a goat with reader surveys showing 80-90% incorrect staying preference [12].” Morone, A. and Adibpour, N. said “Switching increases win probability, from which it is more obvious to see the difference in the probability of those two doors [10].” Finally, using the programme with Python code to simulate the theoretical situation gives evidence of their statements, as shown in Table 1, with a visual line graph to have a more obvious comparison, as shown in Figure 1.

import random

import platform

import asyncio

def stick_simulation(trials):

"""Simulate MHP where player sticks with initial choice."""

wins = 0

for _ in range(trials):

# Set up 3 doors: 1 = prize, 0 = goat

doors = [0, 0, 0]

prize_door = random.randint(0, 2)

doors[prize_door] = 1

# Player chooses a door randomly

player_choice = random.randint(0, 2)

# Check if player wins by sticking

if doors[player_choice] == 1:

wins += 1

return wins / trials

def switch_simulation(trials):

"""Simulate MHP where player switches to remaining door after host reveal."""

wins = 0

for _ in range(trials):

# Set up 3 doors: 1 = prize, 0 = goat

doors = [0, 0, 0]

prize_door = random.randint(0, 2)

doors[prize_door] = 1

# Player chooses a door randomly

player_choice = random.randint(0, 2)

# Host reveals a goat door (not prize or player's choice)

possible_reveals = [i for i in range(3) if i != player_choice and doors[i] == 0]

reveal_door = random.choice(possible_reveals)

# Player switches to the remaining unopened door

switch_choice = [i for i in range(3) if i != player_choice and i != reveal_door][0]

# Check if player wins by switching

if doors[switch_choice] == 1:

wins += 1

return wins / trials

async def main():

# Run simulations for sticking and switching (100 trials each)

trials = 100

stick_win_rate = stick_simulation(trials)

switch_win_rate = switch_simulation(trials)

# Print results

print(f"Sticking win rate (100 trials): {stick_win_rate:.3f} (Expected: 0.333)")

print(f"Switching win rate (100 trials): {switch_win_rate:.3f} (Expected: 0.667)")

if platform.system() == "Emscripten":

asyncio.ensure_future(main())

else:

if __name__ == "__main__":

asyncio.run(main())

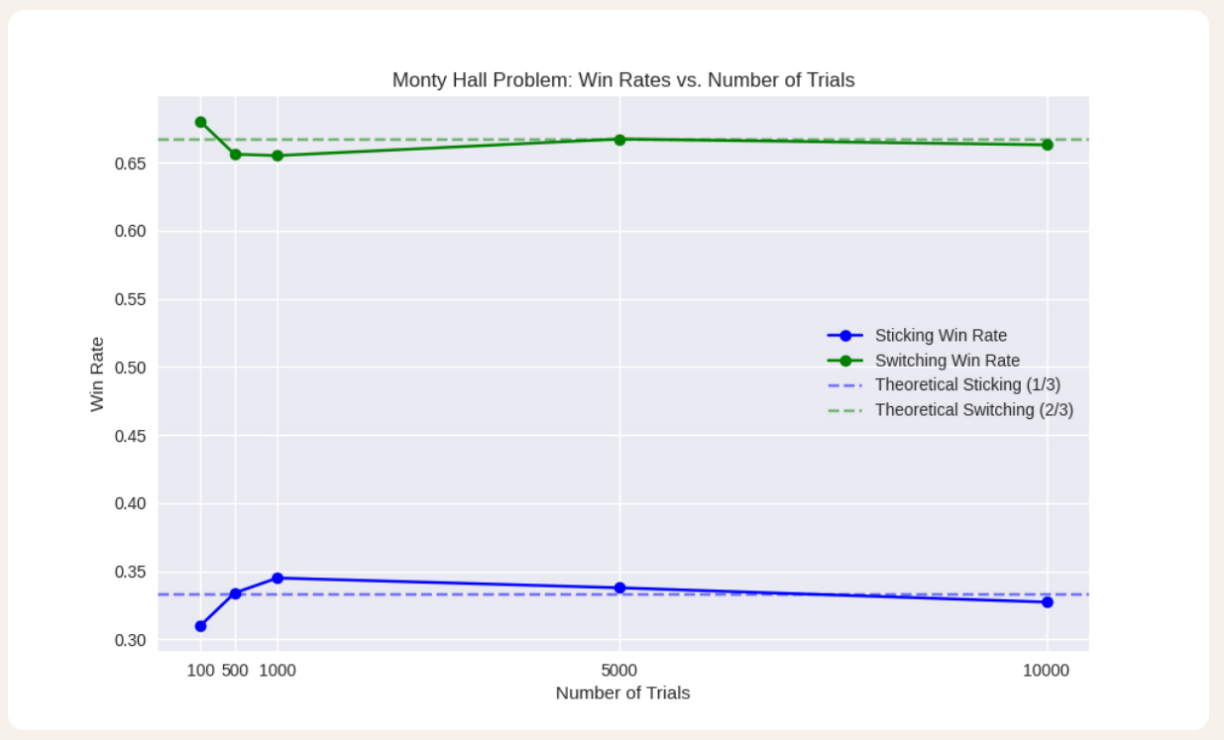
From Table 1 and Figure 1, it is more certain that the probability in each case is different, with the sticking win rate being half the switching win rate. Furthermore, using the probability method to find the corresponding probability in each case gives:

Assume there are three doors and first choose door A, then the host will open one door from B or C, which does not have a prize behind it:

$$ P\left(sticking win\right)=P\left(prize is behind A\right)=\frac{1}{3}$$(2)

$$ P\left(switching win\right)=P\left(prize is either behind B or C\right)=\frac{2}{3}$$(3)

Cognitive bias Results: Juslin stated, “people often violated the rule that:

$$ P\left(A\&B\right)\le P\left(A\right)$$(4)

$$ P\left(A\&B\right)\le P\left(B\right)$$(5)

which is the basic law of probability theory [9].” Also, extensive amounts of data on multiple-cue judgment likewise suggest that the judgment is often a linear additive combination of the cues. Additionally, from Wilcox, J.E. “likelihood neglect would occur if participants were aware it was more likely that the opened door would be opened if the unselected and unopened door concealed the prize, but they did not think the unselected and unopened door more probably concealed the prize as a result.” which also provides a common cognitive bias that could lead to incorrect choices [3]. Finally, Saenen, L. claims “This equiprobability bias not only occurs in the MHD but leads students to errors in a wider range of probabilistic problems,” where people always assume the situation in a straightforward way (equiprobability for both doors), but usually it is wrong [15].

Application outcome: Lindley claims that “the conditional probability is helpful in medical diagnosis [8].” After applying Bayes’ rule to the test result, the probability of the patient having hepatitis increases in different degrees depending on the sensitivity of the test. With some special information about this particular patient, the doctor can utilise their knowledge to provide a more accurate result for them. This proves how conditional probability can be used to refine medical diagnoses. Another example in medical risk assessment was conducted by Borsetto, D. who examined the recurrence risk of Head and Neck Squamous Cell Carcinoma (HNSCC) using conditional probability, they tell “the study calculated the probability of recurrence at specific time points after surgery, given that the cancer had not recurred to that point—with the first year 17.3%, second year 9.6%, etc., where the conditional probability model allows clinicians to offer more personalised follow-up service for patients [13].” Additionally, Silva wrote that “conditional probability in supply chain can accurately model and assess risk dependencies, where the occurrence of one risk may influence or increase the probability of other risks [7].” Combine with ANP and MCS for calculating probabilities, and Bayesian theory to incorporate dependency between risks, which allows for a more dynamic and interconnected risk model. It also ensures that realistic risk propagation is considered in the supply chain, enabling companies to develop more effective strategies. Lastly, in the financial risk measures, Martin, J. discussed a new Bayesian method for estimating financial risk measures, especially an informative prior Bayesian (IPB), which was used to “incorporate all available information from the data and assign different weights to data in different places, which improves the accuracy of risk estimates [14].” This method was also used for forecasting VaR and CVaR and provided more stable predictions than other models.

Despite the fact that conditional probability works well when the conditioning event is observable and exogenous, this tool usually fails when the event is strategic or noisy. When facing situations that involve human inner thought and decision-making, it becomes difficult for conditional probability to work well, as there may be several qualitative factors and a human’s inner emotions that cannot be quantified. Additionally, due to people’s varying levels of cognitive bias, the choice also becomes unpredictable unless others have a comprehensive and thorough understanding of this person, which involves numerous psychological studies, making it difficult to handle using mathematical tools. For instance, in Berthet V’ paper “Baker and Nofsinger (2002) reported a finding from a survey in Gallup in 2001, revealing that on average, investors estimated that the stock market return during the next 12 months would be 10.3% while estimating that their portfolio return would be 11.7% [17].” This shows the overconfidence of investors due to their own cognitive bias—they believed the market would return 10.3%, but they thought they could outperform the market with a return of 11.7%. Secondly, in the same paper but in medicine area, “Blumenthal-Barby and Krieger (2015) reported the following finding: 82% of the studies (N=175) were conducted with representative populations and 68% of the studies (N=145 studies) confirmed a bias or heuristic in the study population; the most studied CB are loss/gain framing bias (72 studies, 24.08%), omission bias (18 studies, 6.02%), relative risk bias (29 studies, 9.70%), and availability bias (22 studies, 7.36%) [17].” This statistic highlights that 68% of the studies in the medical field confirmed the presence of cognitive biases and breaks down which biases were most prevalent. Among those two studies in different fields, both suggest that debiasing methods such as improving financial literacy or enhancing decision-making protocols in healthcare could help reduce the influence of cognitive biases on professionals’ judgments.

5.  Discussion

In general, those models based on conditional probability provide a more accurate and realistic estimate of real-world situations, as they include several factors that may affect people’s choices when calculating it. This method is best suited for problems involving counterintuitive probability puzzles and Bayesian reasoning under uncertainty, such as decision-making in games or lotteries where initial choices must be revised based on new evidence (e.g., dynamic financial risk assessment, economic fields, and medical diagnosis).

From the idea of MHP, which not only involves human cognition but also links to the objective probability behind each door, psychological research can also be built from this case, which can discuss how human cognitive bias may affect their objective decision after thought with their knowledge. It is also suggested that engineer can develop adaptive Bayesian algorithms for dynamic MHP variants, or the machine-learning ability of AI tools based on the conditional probability idea, which can help those AI be more personal to their users. By learning the user's behaviour, it can also predict and understand the user’s meaning, despite their words sometimes being less correct or standard.

However, as stated previously, people may frequently rely on their own experience, no matter whether it is reasonable or not, which may seriously affect their choice and make the conditional probability result fail to pair with their choice. Also, recent applications of conditional probability are usually concentrated in some specific areas, it has limited yields, and sometimes it may be quite difficult and costly to collect all the data needed. Be more specific, conditional probability usually works well in experimental cases, but when it links to humans, people may often overweight recent, dramatic evidence while underweighting stable background probabilities when updating beliefs. This can distort conditional probability assessments in real-world situations like financial decisions, where market news overshadows long-term trends. Additionally, as seen in “Sampson’s paradox”, conditional probability can produce counterintuitive or misleading results in aggregated data due to lurking variables or unequal group size. Lastly, in empirical applications, conditional probability could fail if the underlying conditions assumed are violated. For instance, medical diagnosis may fail to provide a comprehensive analysis as the human body is dynamic; there may be some underlying issues that are assumed to be none, but in the real world, may occur anew. Along with the subjectivity of humans, this result may not always be the best choice for humans in the real world, as there may be more factors they consider when making decisions. Despite this, the trend of an increasing number of real-world situations can be handled by conditional probability rather than by directly trying to calculate probability.

6.  Conclusion

The central theme of this paper is evaluating the strengths and limitations of conditional probability through the Monty Hall Problem, which shows its critical role in decision-making under uncertainty environments. The significance lies in constructing a bridge from theoretical probability to practical applications, revealing how conditional reasoning enhances outcomes in different fields like medicine and finance, while exposing persistent cognitive barriers. The MHP serves as a powerful lens to explore these dynamic variables, empirically, with  $$ \frac{1}{3} $$ probability wins the prize when sticking to their choice, and  $$ \frac{2}{3} $$ probability wins the prize when switching their initial choice after the host provides more information. For this result, several assumptions are made, such as without cognitive bias and mental effect of the participants, the host is always saying true facts, there is exactly one prize and is randomly placed after one door, and lastly, most important, the door is invisible by the participant, otherwise the probability of winning the prize will become 1 for normal participant. Simulations of this experiment based on those assumptions are also conducted, results are shown in Table 1 and Figure 1which both showed an obvious comparison of those two choices. The discussion part also offers an insight into both normative solutions and human judgment errors.

On the other hand, potential gaps remain in addressing dynamic, real-world complexities and scaling bias mitigation. Current studies often rely on simplified models, which ignore several factors that may affect the outcomes in real-world settings. Additionally, educational strategies require broader implementation to address pervasive biases effectively.

Further research could explore more adaptive algorithms that integrate conditional probability with machine learning to handle dynamic data. For instance, some practical future directions may include improved decision models, such as Markov Decision Processes (MDPS), that could be expanded to include real-time data processing, where the algorithm updates its decision-making strategy based on newly available data. Additionally, some hybrid models that combine heuristic and normative approaches to enhance the accuracy of decision-making can also be improved through investigations of the optimal combination of heuristic-based models and normative models. The overall performance may improve significantly when the model has the best-suited combination of those two approaches. Lastly, Scalable pedagogical tools that can use simulations and interactive platforms with AI-powered training simulations could further improve public understanding of conditional probability, as these tools could adapt to the learner’s decision-making process and offer personalized feedback to help them recognize their cognitive biases, fostering their stronger adaptability in more complex contexts.