1. Introduction
For algebraic number theory [1], the overall understanding process starts with defining some basic algebraic number theory annotations, such as algebraic numbers and integers [2], number fields, rings of integers, norm and discriminant, fractional ideals, and class groups and lattices. As one of the most essential parts of algebraic number theory, factorising prime numbers into prime ideals of a ring of integers and applying it in the case of simple number fields (such as quadratic fields) is very important intermediate knowledge. Only after mastering the basic definition and such a decomposition relationship can the following Minkowski’s first theorem be introduced to try to compute class numbers and class groups of simple number fields. This paper can be divided into two parts, describing the process of decomposition of prime ideals and the corresponding applications, respectively. To be more specific, it discusses what kind of prime numbers can be written in the form of a sum of two integer squares, which is a very classical part of algebraic number theory.
The most important part of the first part is that if we give a number field, give the corresponding ring of integers and have a minimal polynomial, then we can perform in the given number field for some given prime numbers. break down. The second part gives more inspiration when we consider an algebraic decomposition problem, in addition to analyzing the properties of the number itself, we can also use the properties of groups, rings, and fields on the basis of group theory. Considering the problem, this actually inspires us to think about the problem from many aspects when facing Fermat's last theorem.
2. Factoring primes
2.1. Some basic definitions
Several concepts of algebraic number theory have a pivotal role [3]: numbers, polynomials, and equations. So this paper gives definitions of some of the core terms before discussing the central issues. First of all, for numbers that people have a lot of contact with, the more special numbers in algebraic number theory are algebraic numbers and transcendental numbers [4]. Based on this background, the following are some definitions.
Definition 2.1. A complex number is called algebraic if there is a non-zero polynomials
is called algebraic if there is a non-zero polynomials with
with . If
. If is not algebraic, it is called transcendental.
is not algebraic, it is called transcendental.
Definition 2.2. The number field generated by an algebraic number is the smallest subfield of
is the smallest subfield of that contains
that contains . We denote this field by
. We denote this field by .
.
A subfield is an algebraic number field (or a number field) if
is an algebraic number field (or a number field) if for an algebraic number
for an algebraic number .
.
Definition 2.3. A complex number is an algebraic integer if there is a monic polynomial
is an algebraic integer if there is a monic polynomial with
with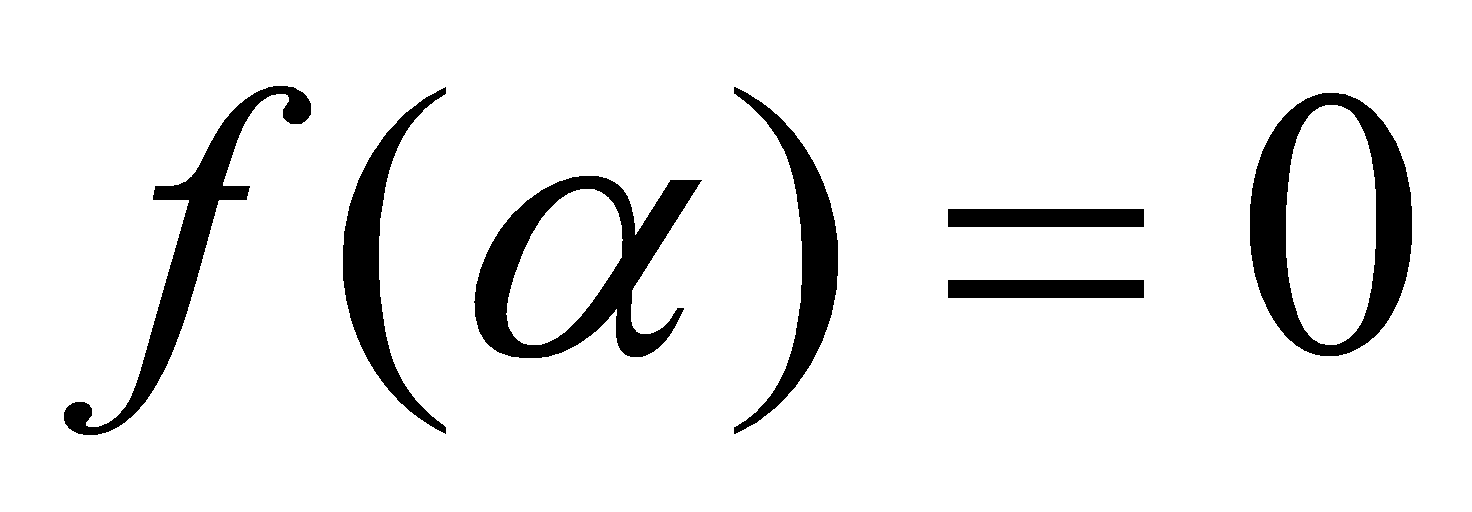 .
.
Definition 2.4. Let be a number field. The ring
be a number field. The ring consisting of all algebraic integers in
consisting of all algebraic integers in is called the ring of integers of
is called the ring of integers of , where the set
, where the set of algebraic integers is a subring of
of algebraic integers is a subring of .
.
2.2. Prime ideals
Lemma 2.5. Let be a number field and
be a number field and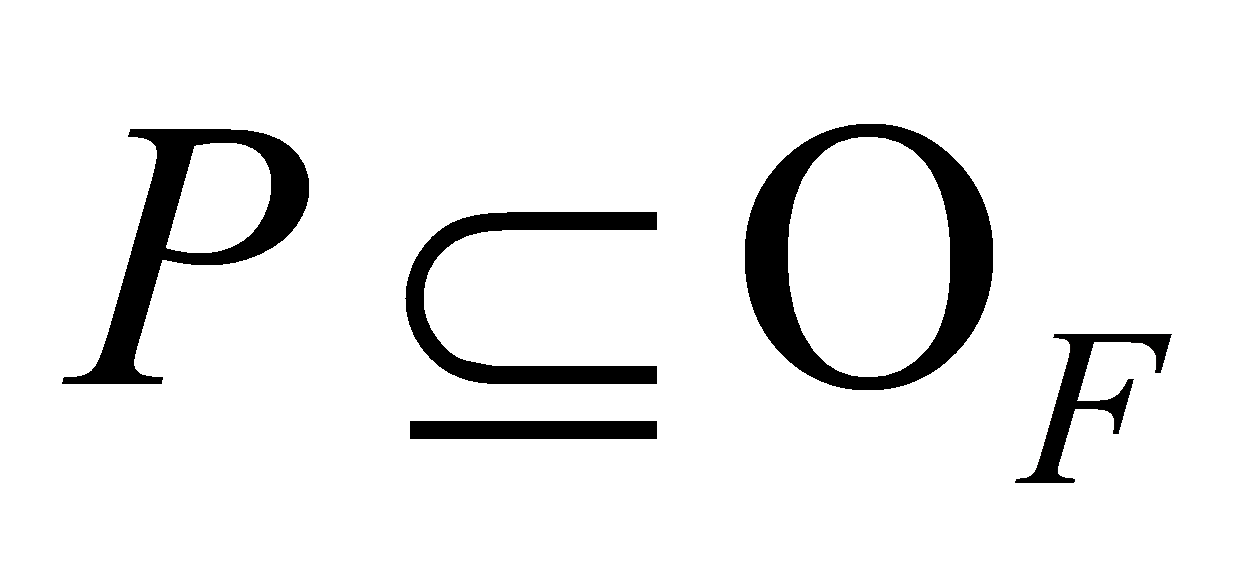 a non-zero prime ideal [5]. Then
a non-zero prime ideal [5]. Then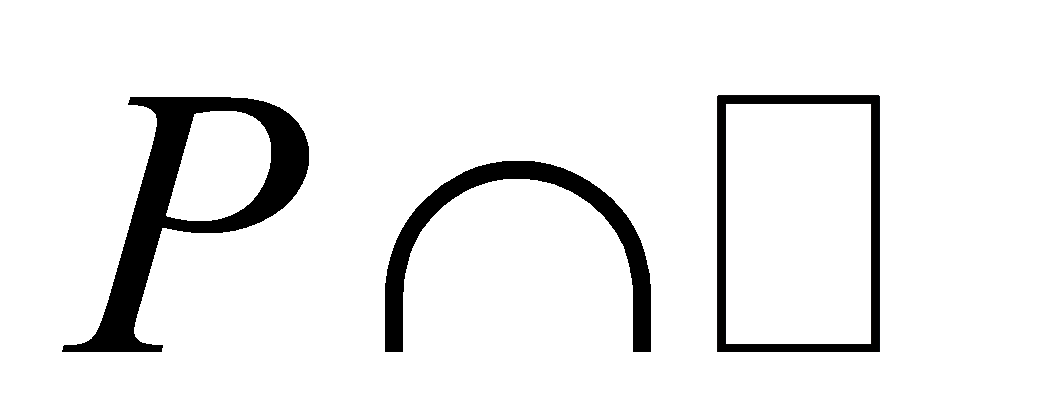 is a non-zero prime ideal of
is a non-zero prime ideal of , so
, so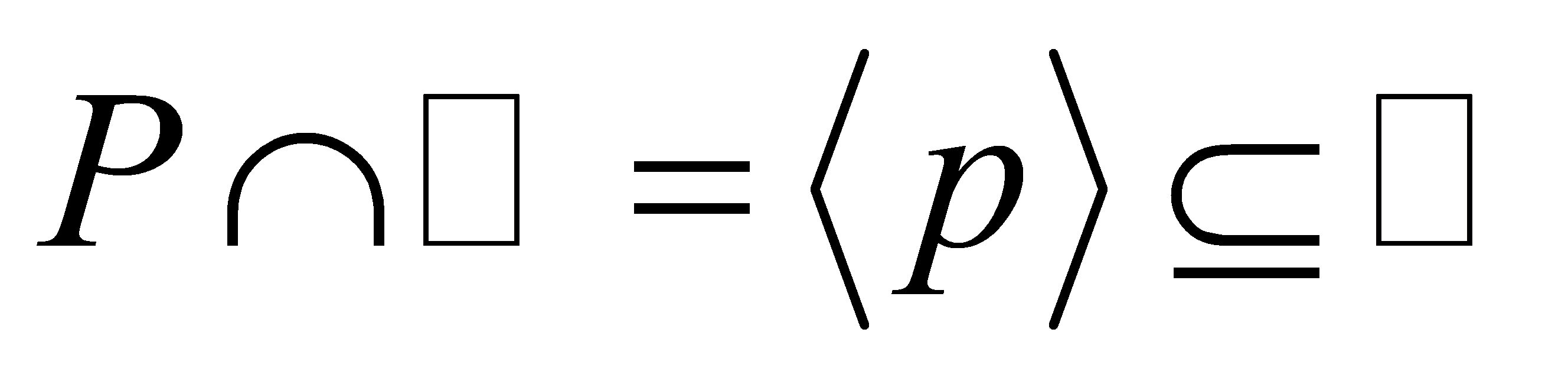 , for a prime
, for a prime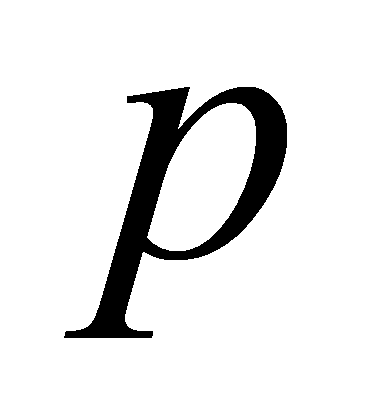 .
.
Proof. If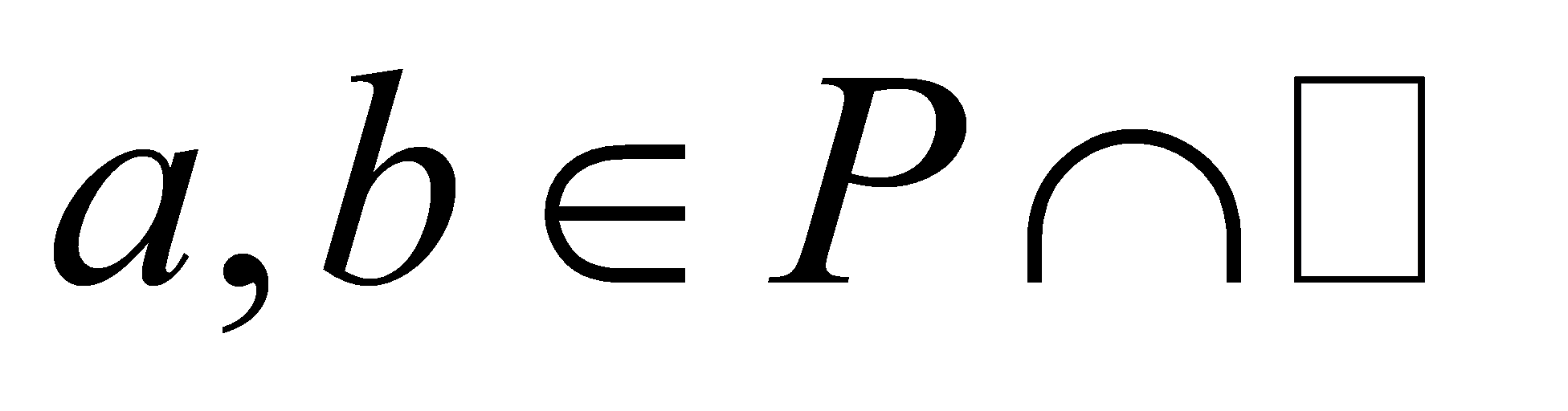 ,
, , then
, then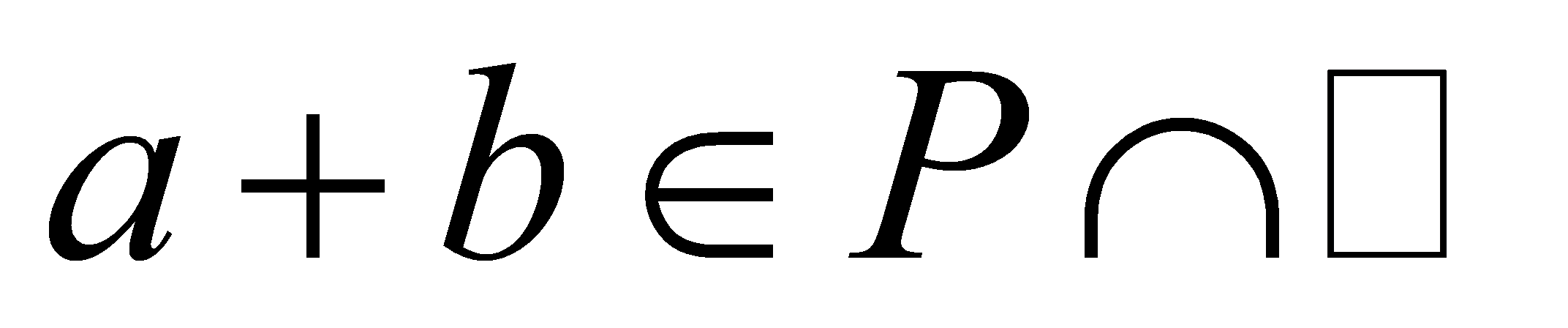 ,
,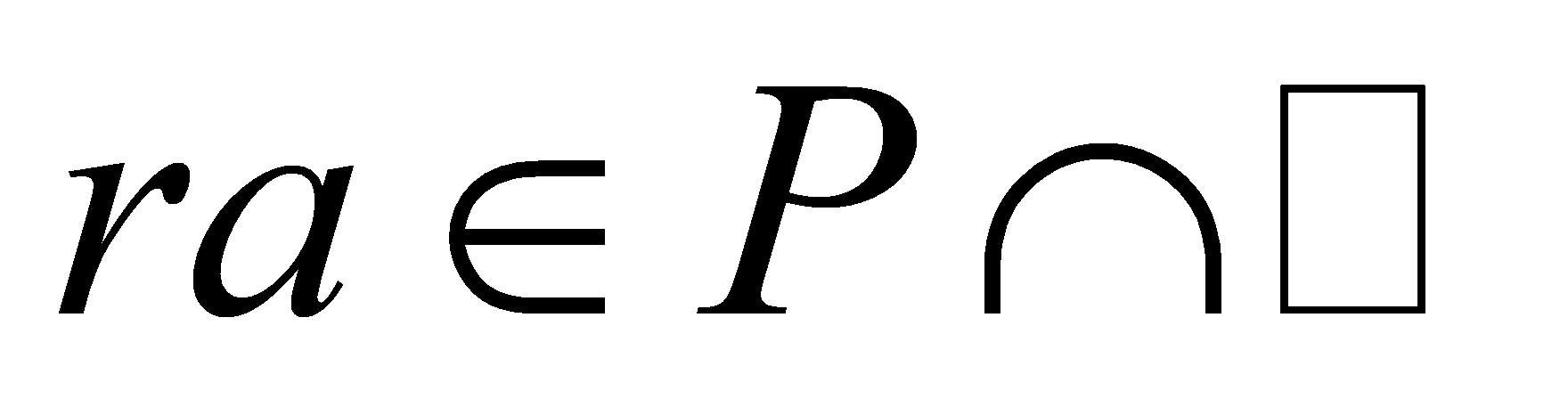 , then
, then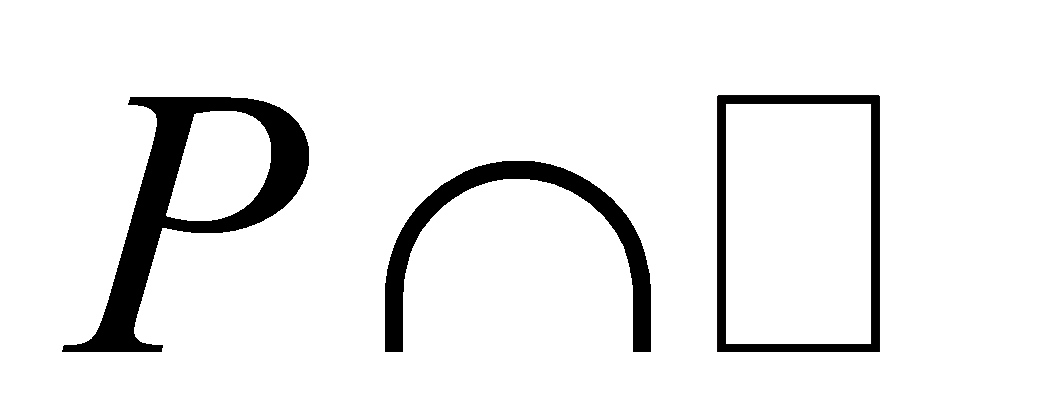 is an ideal of
is an ideal of . If we have
. If we have such that
such that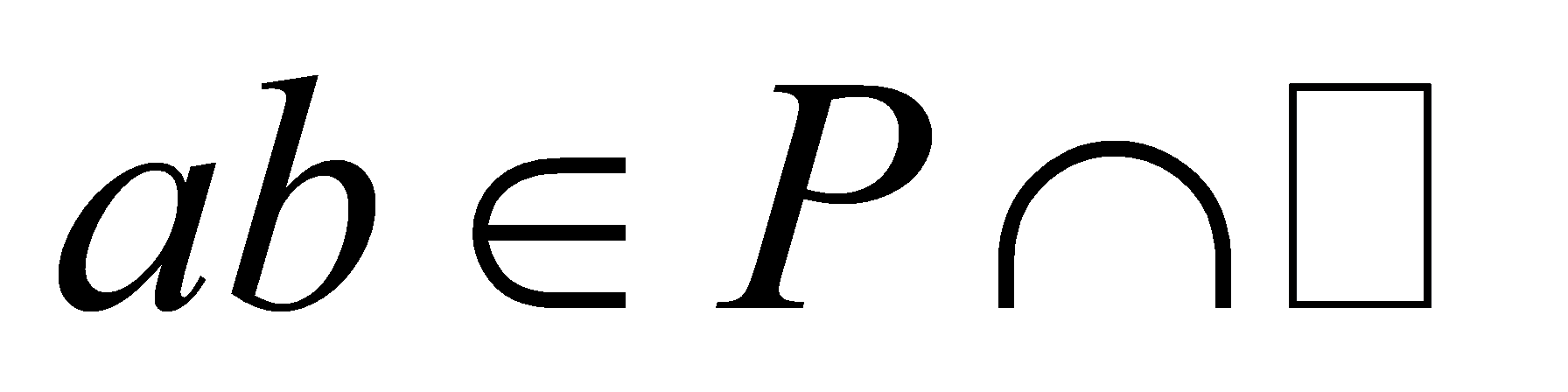 , since
, since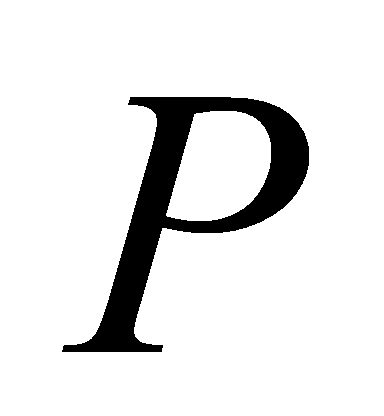 is a prime ideal, then
is a prime ideal, then or
or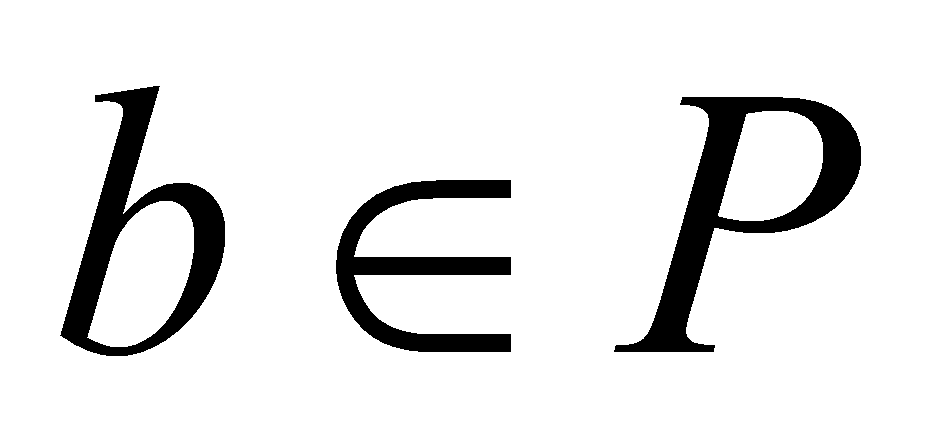 . Since
. Since , we can get
, we can get or
or , thus
, thus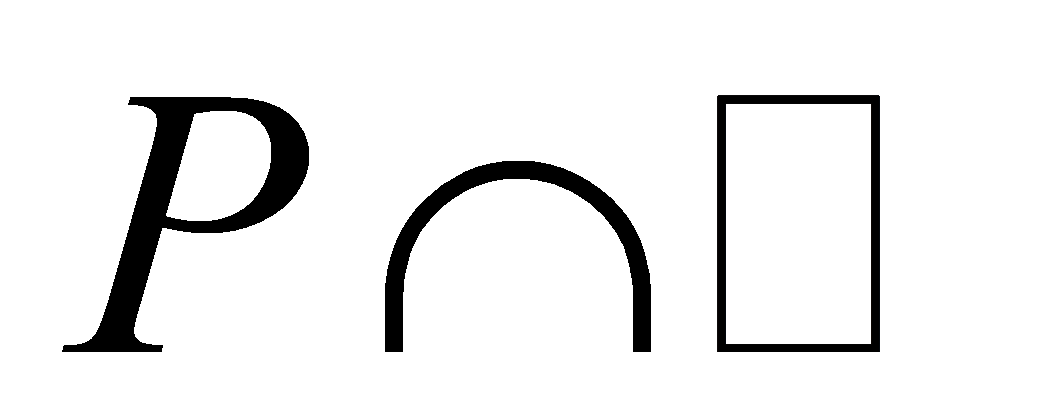 is a prime ideal of
is a prime ideal of . Let
. Let ,
, . We konw that
. We konw that , and
, and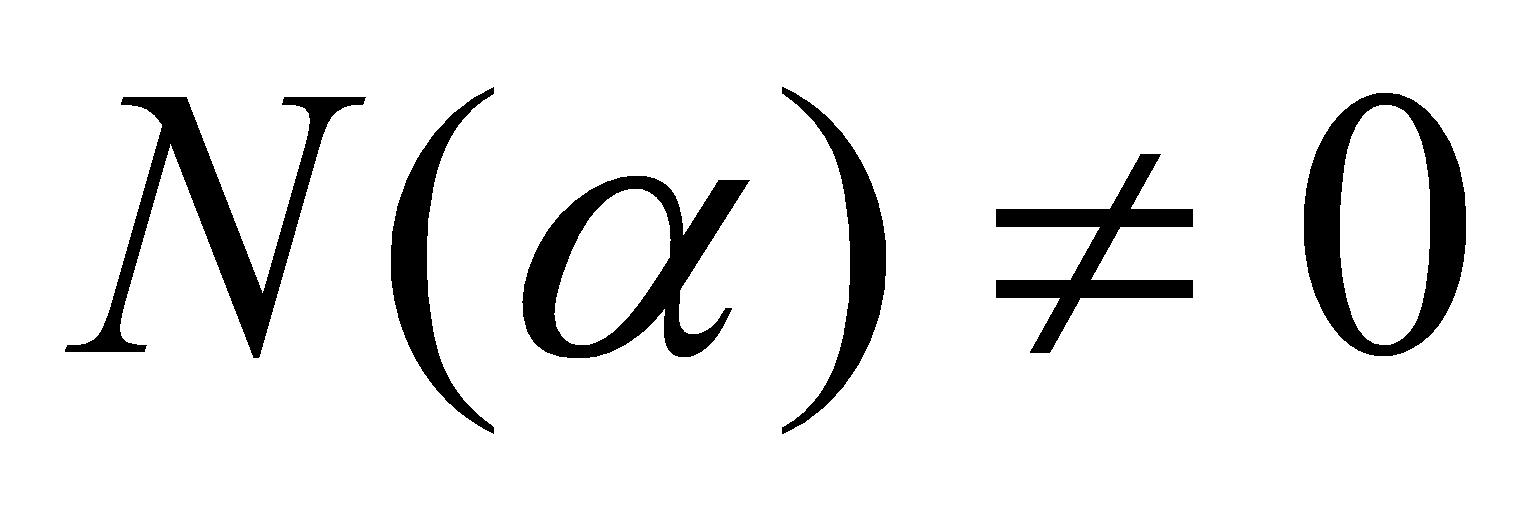 . Hence,
. Hence, . As a non-zero prime ideal of
. As a non-zero prime ideal of , it must have the form
, it must have the form for a prime
for a prime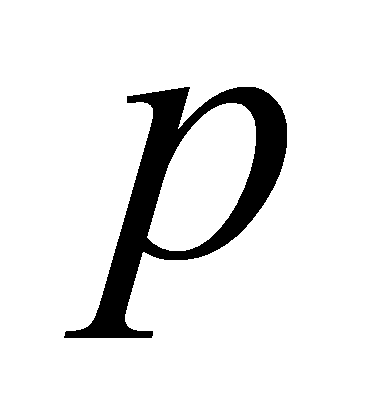 .
.
Definition 2.6. Let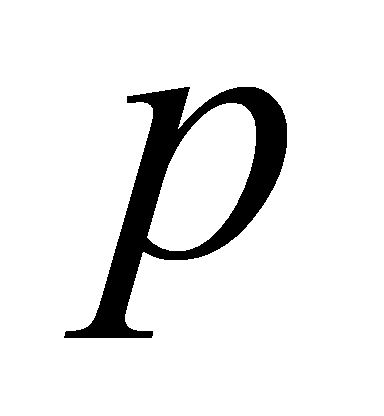 be a prime. The prime ideals
be a prime. The prime ideals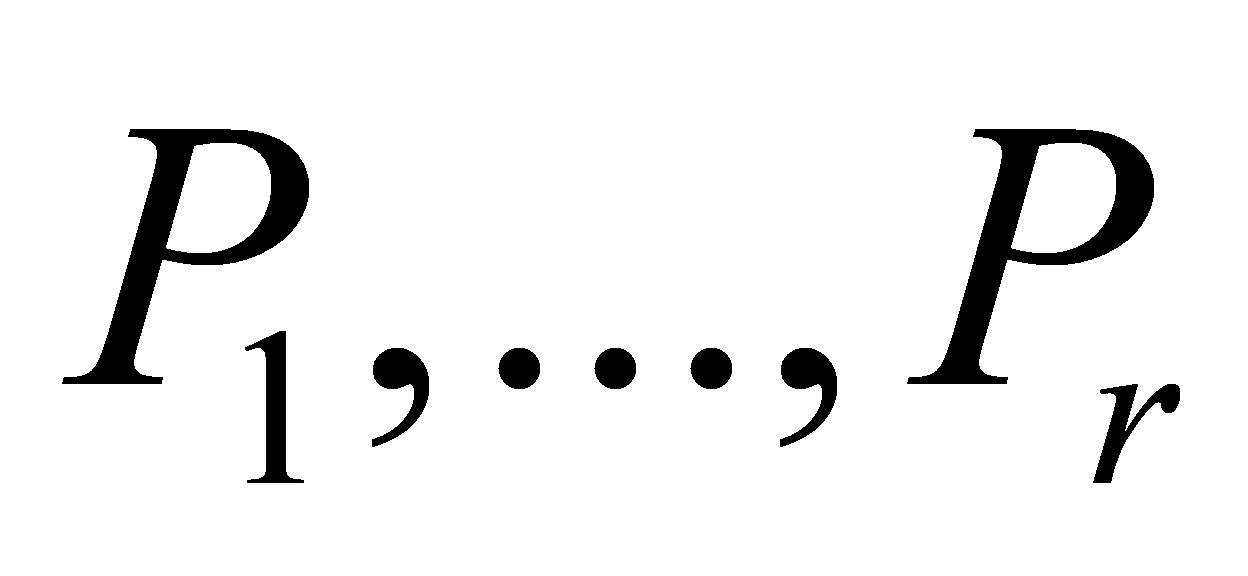 appearing in the prime ideal factorization
appearing in the prime ideal factorization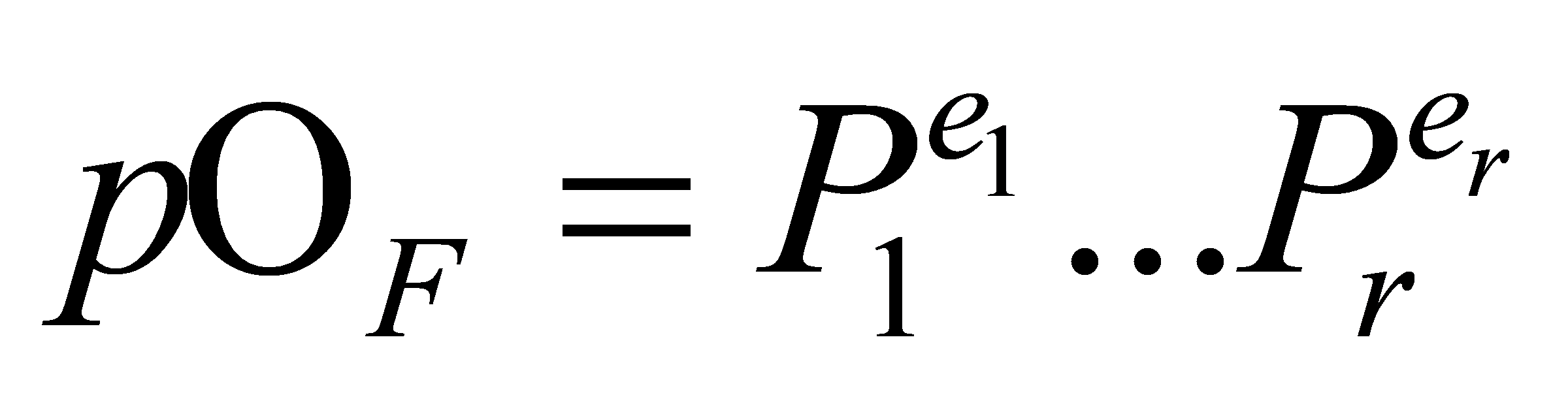 of
of are said to be lying above
are said to be lying above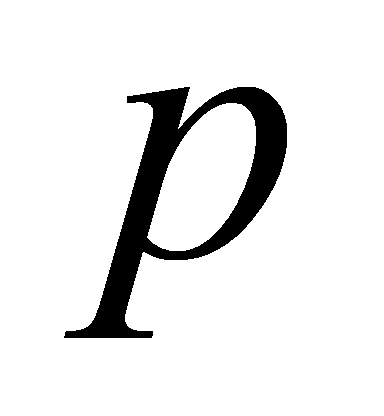 [6].
[6].
Lemma 2.7. Let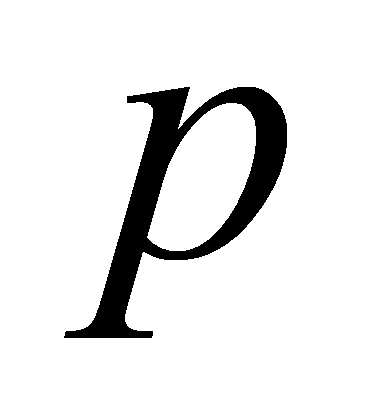 be a prime,
be a prime,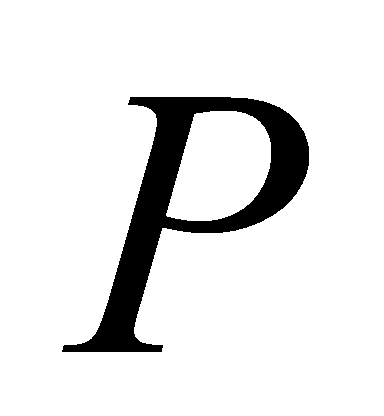 a prime ideal of
a prime ideal of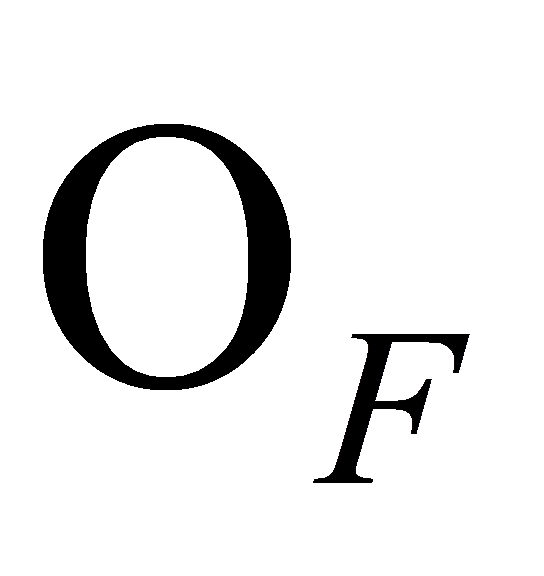 . Then
. Then lies above
lies above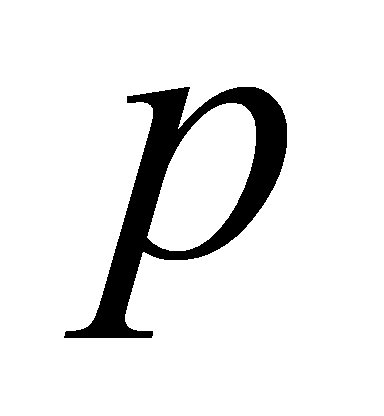 if and only if
if and only if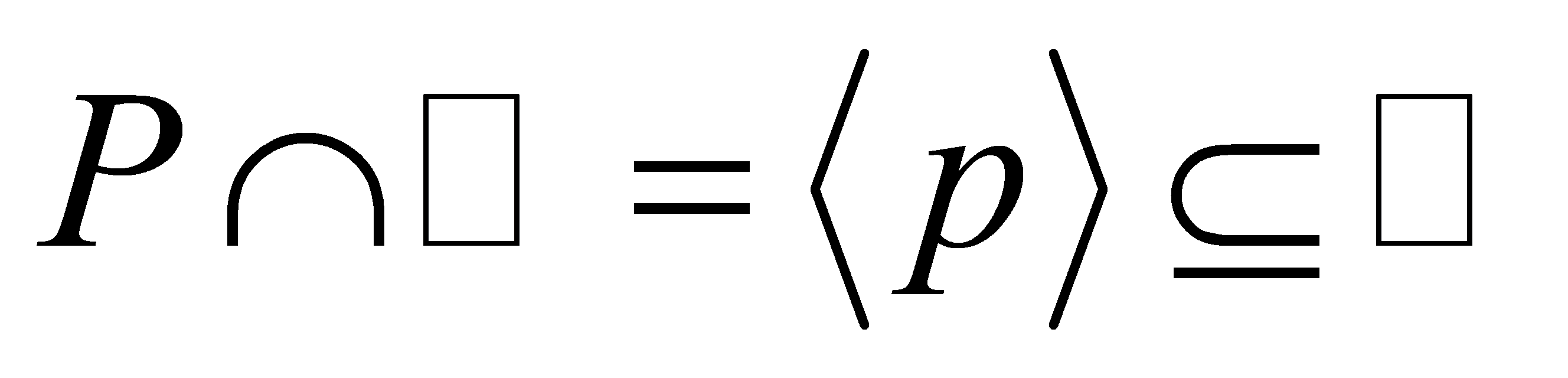 .
.
Proof. If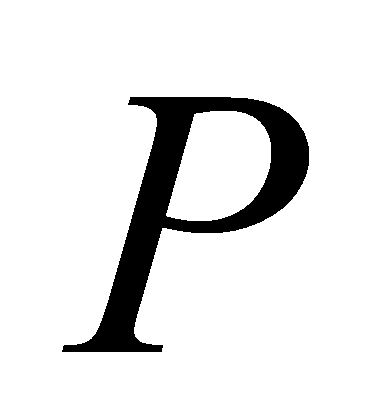 lies above
lies above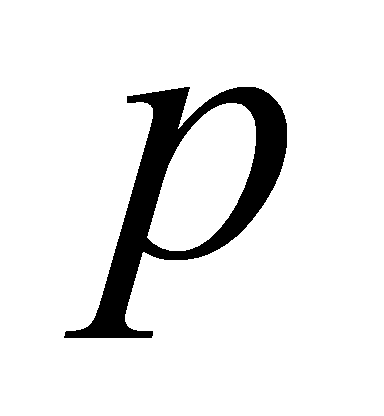 , it appears in the prime ideal factorisation of
, it appears in the prime ideal factorisation of 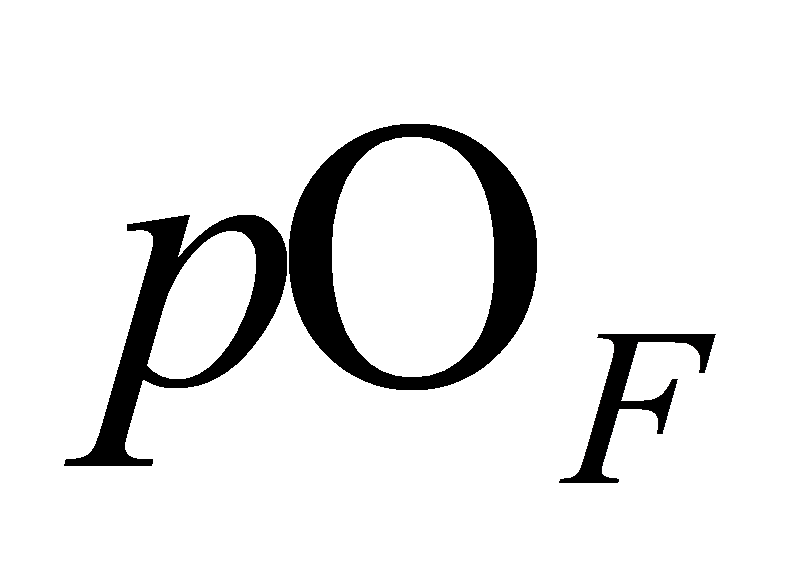 . Thus,
. Thus,  . Then,
. Then,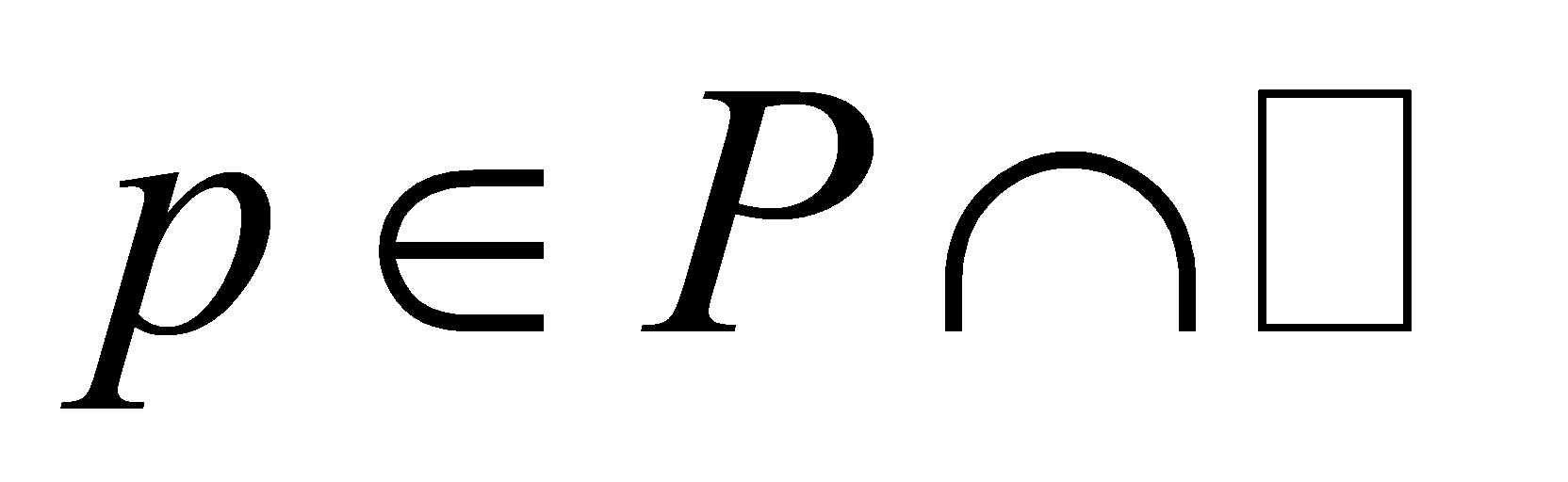 . Since
. Since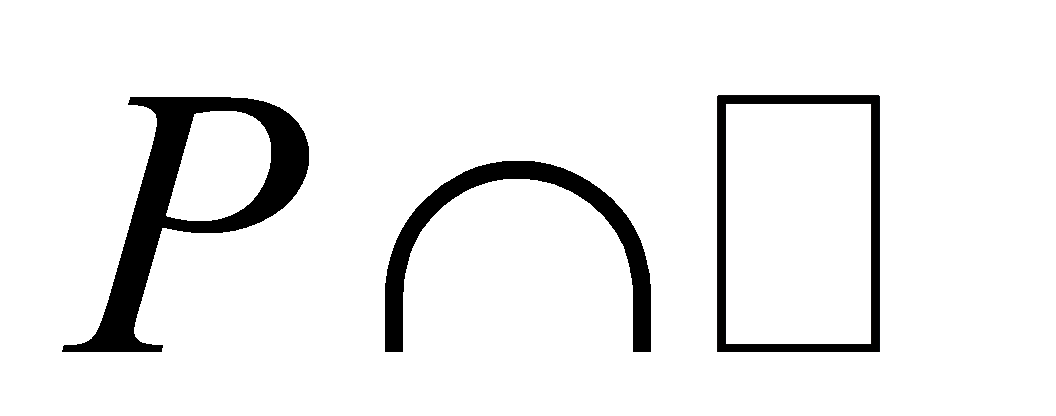 is a prime ideal
is a prime ideal by Lemma 2.5, with
by Lemma 2.5, with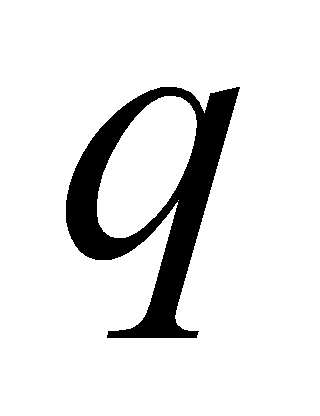 is a prime, then it can get
is a prime, then it can get  , thus
, thus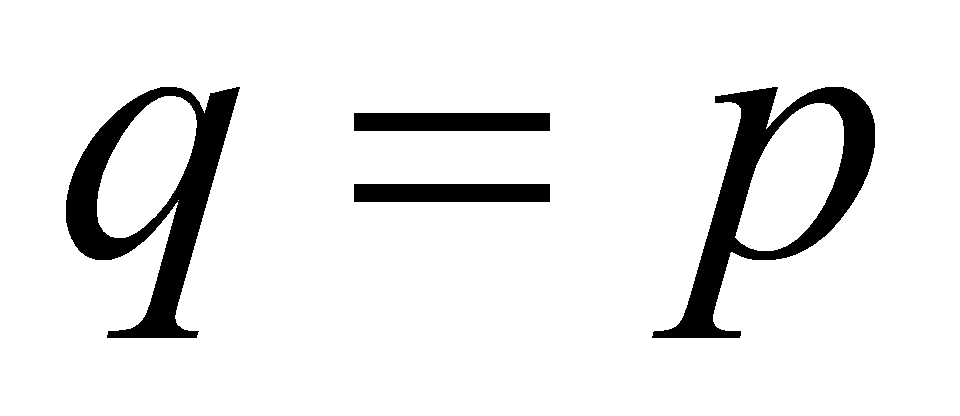 .
.
If , then
, then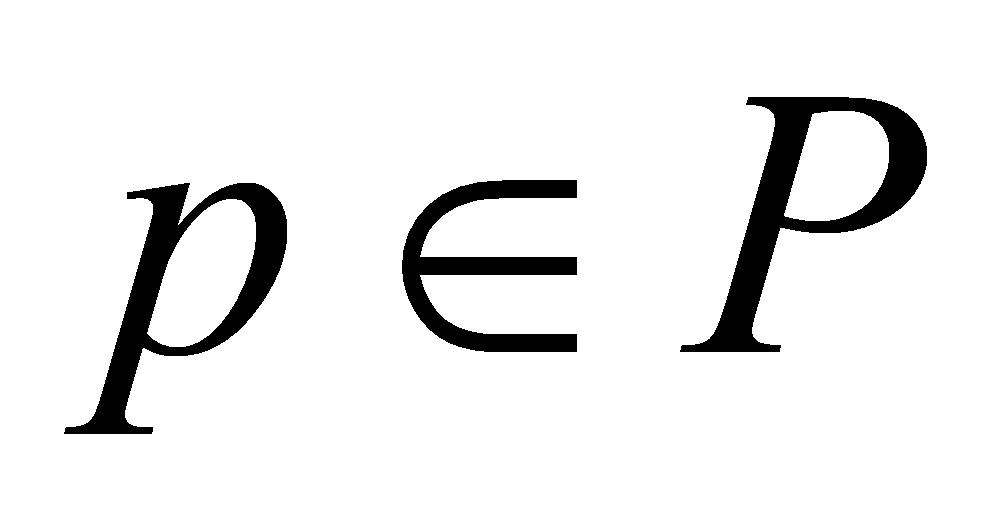 , thus
, thus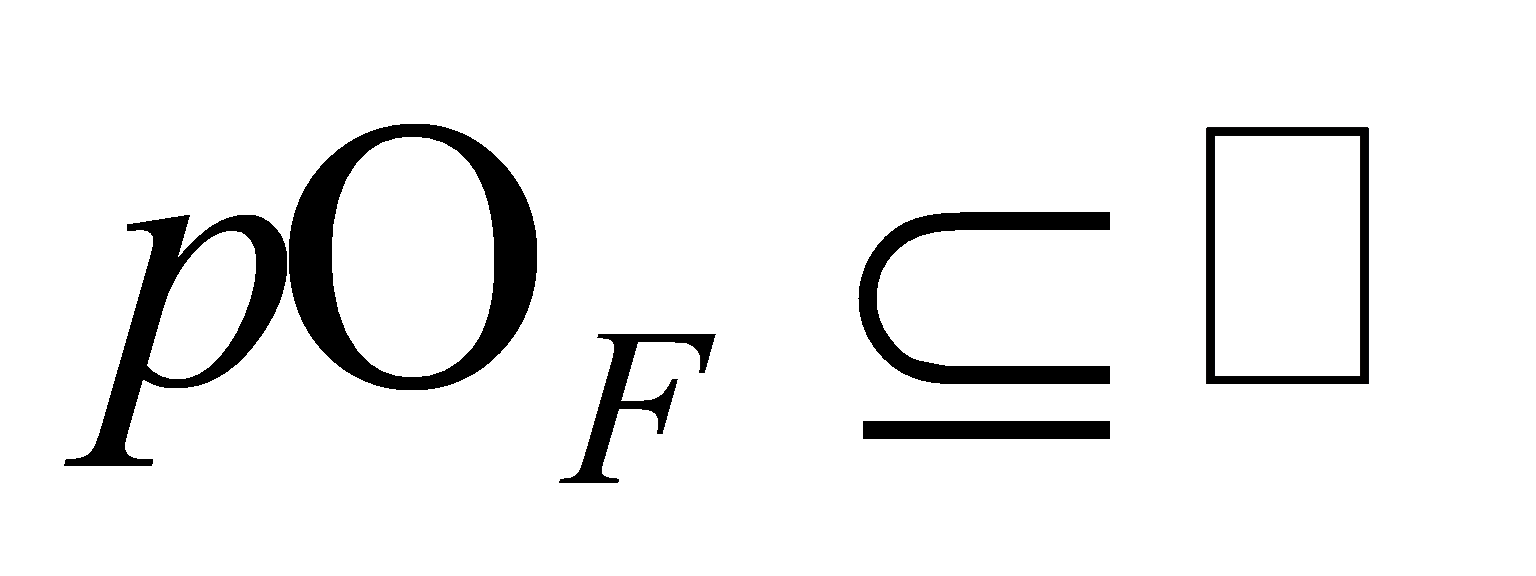 , by the properties of ideals of
, by the properties of ideals of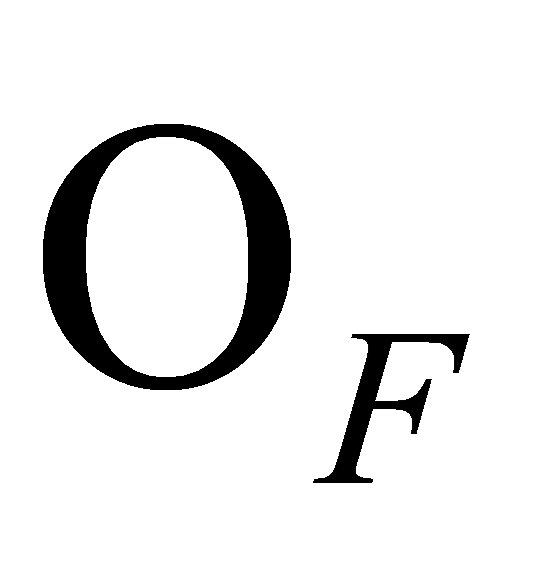 : "To contain is to divide", thus
: "To contain is to divide", thus . Therefore, if
. Therefore, if is the prime ideal factorisation of
is the prime ideal factorisation of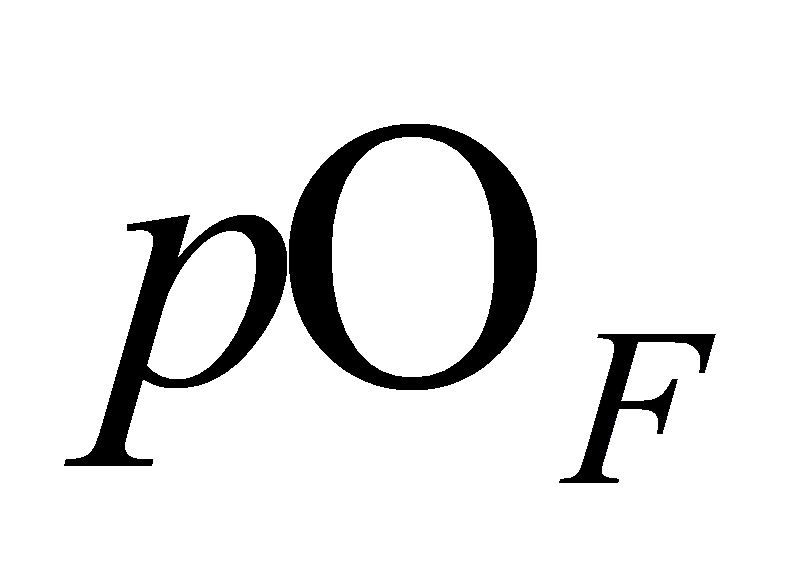 , we must have
, we must have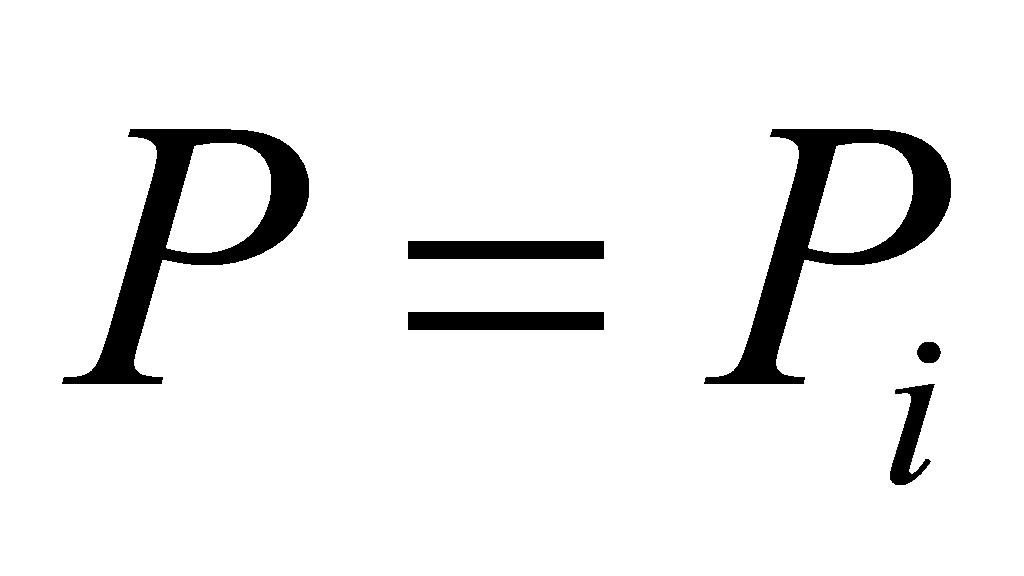 for some
for some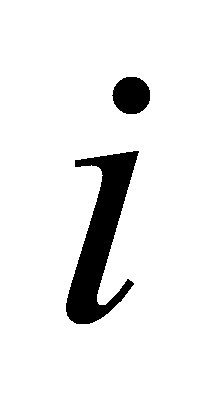 .
.
Theorem 2.8. Let be a number field and assume that
be a number field and assume that , for some
, for some . Let
. Let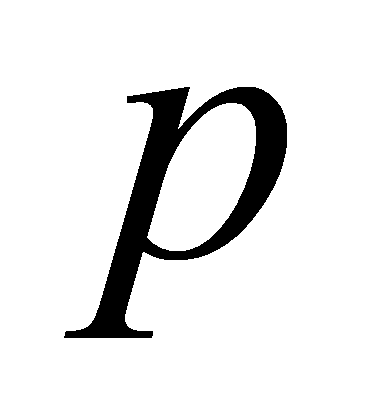 be prime and
be prime and a monic polynomial, such that
a monic polynomial, such that is irreducible over
is irreducible over and divides
and divides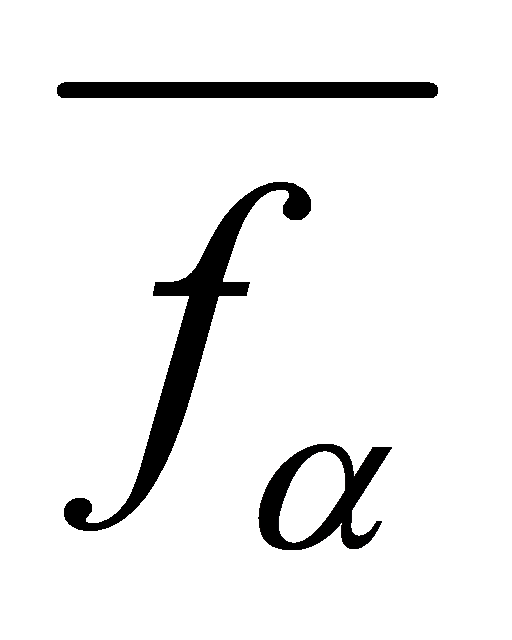 where
where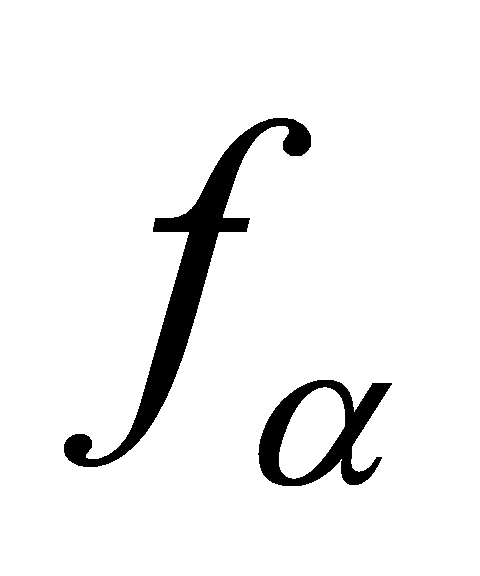 is the minimal polynomial. Then the ideal
is the minimal polynomial. Then the ideal is a prime ideal of
is a prime ideal of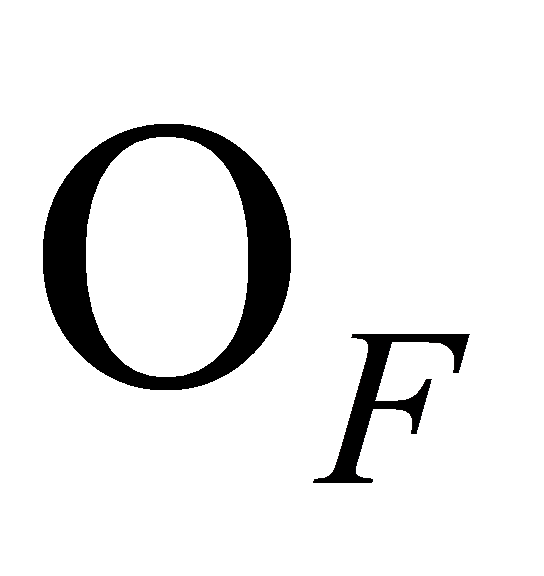 . Moreover,
. Moreover,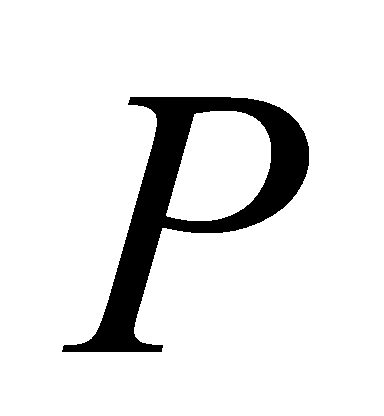 lies above
lies above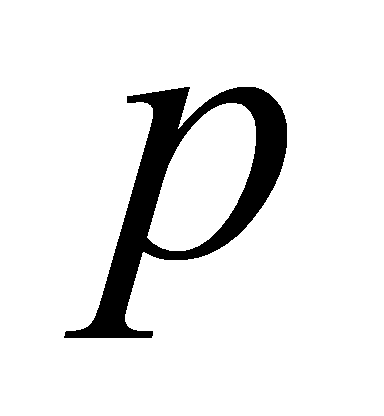 and
and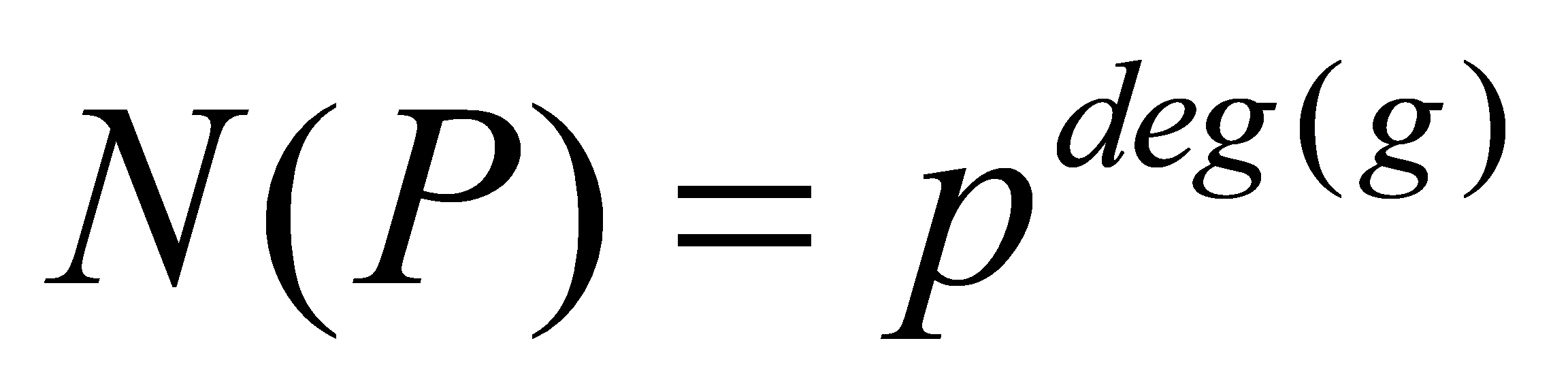 .
.
Proof. We consider the residue class field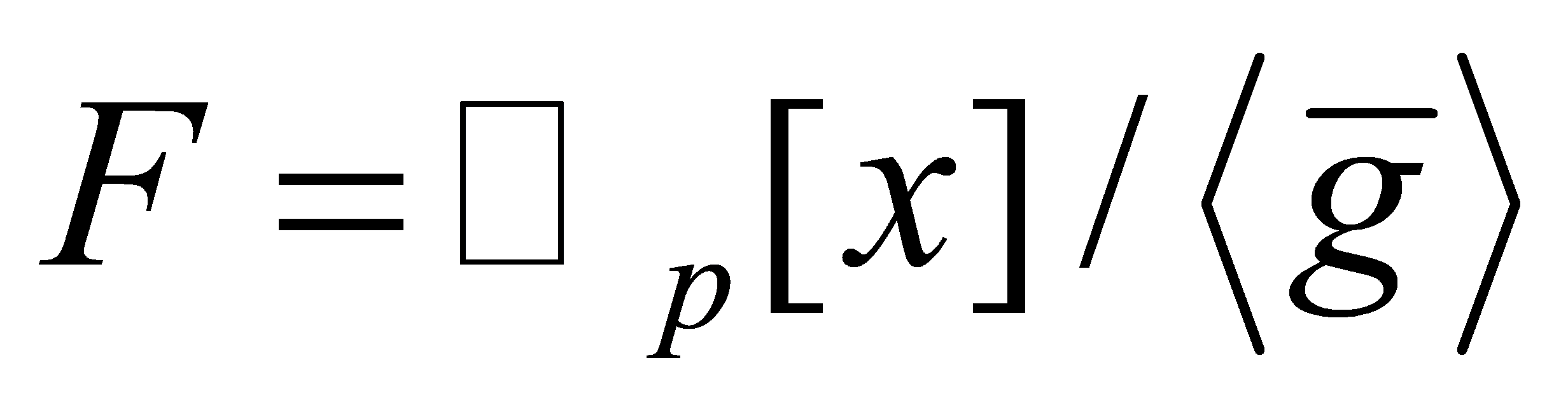 . Recall that
. Recall that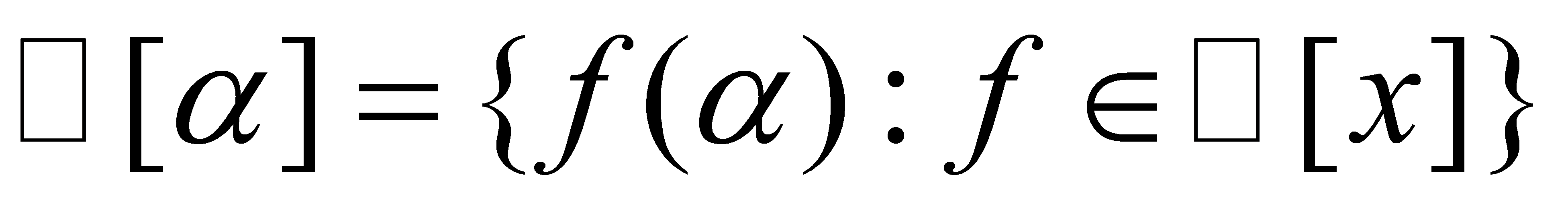 . A function
. A function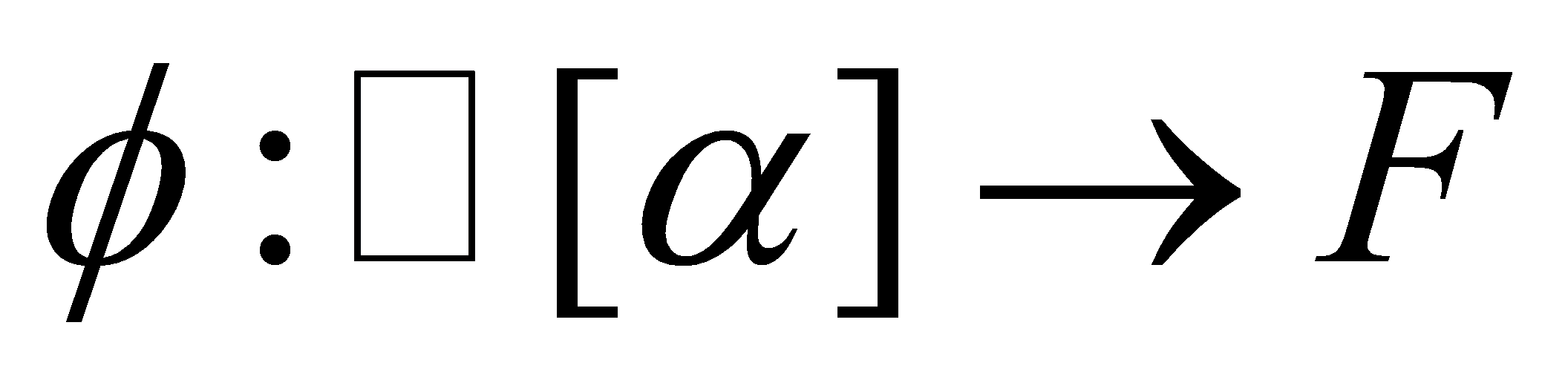 is defined by setting
is defined by setting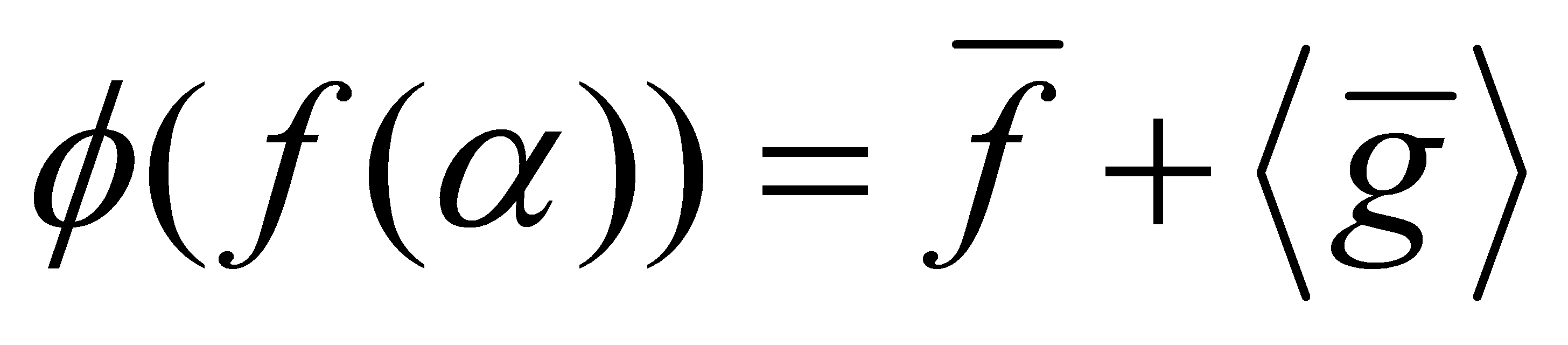 . If
. If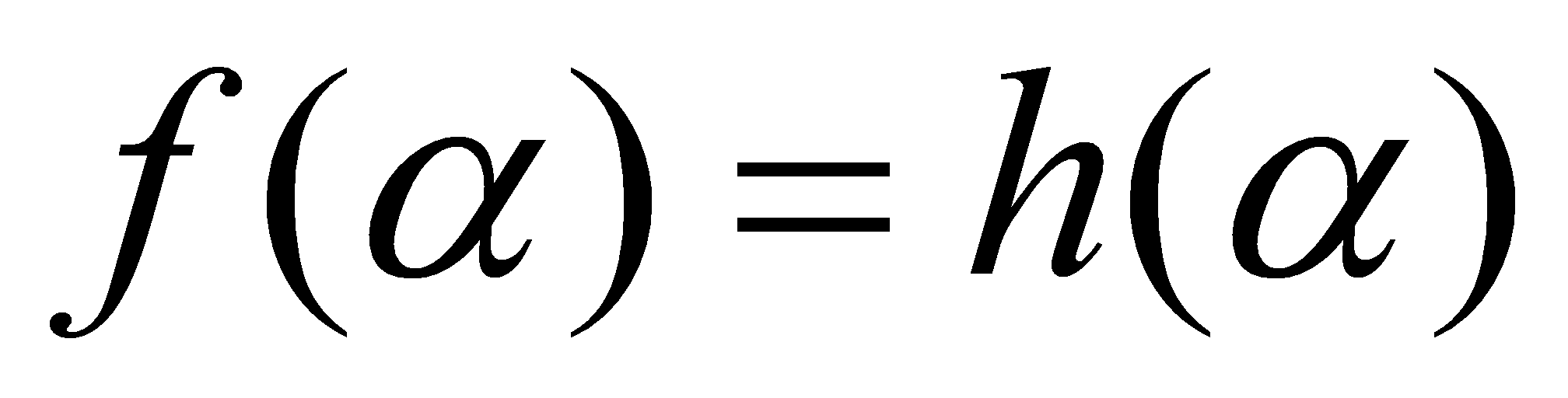 , then
, then divides
divides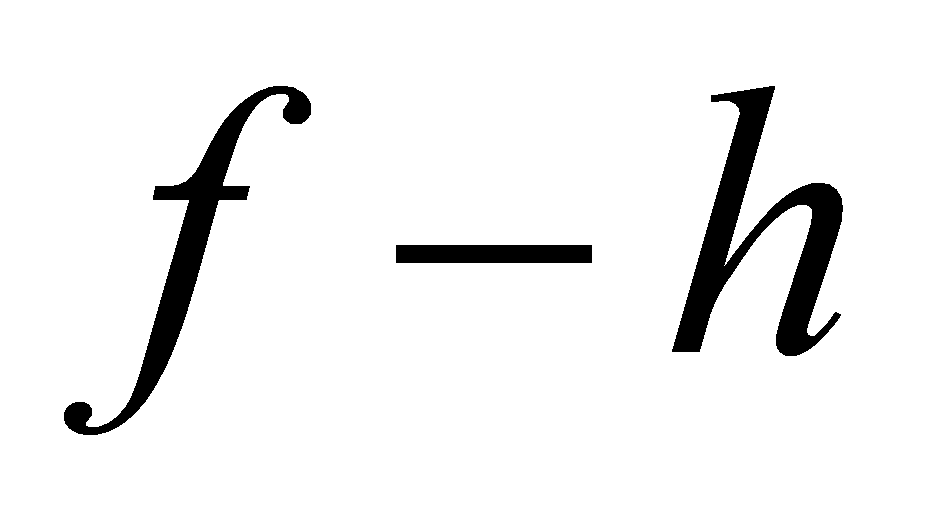 , thus
, thus where
where . By Gauss Lemma, it is found that
. By Gauss Lemma, it is found that , such that
, such that . Since
. Since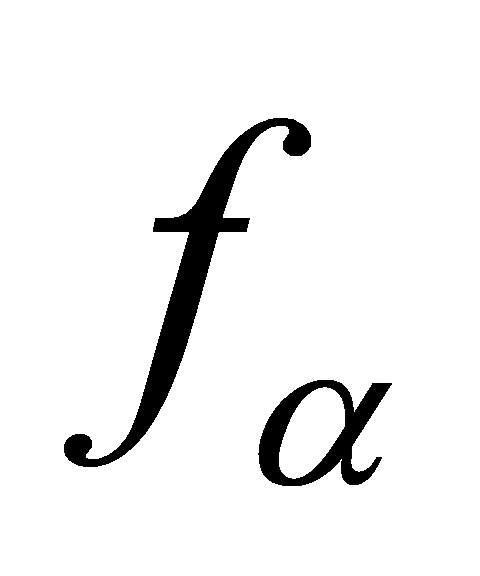 is monic, then
is monic, then . However,
. However, implies that
implies that . Thus
. Thus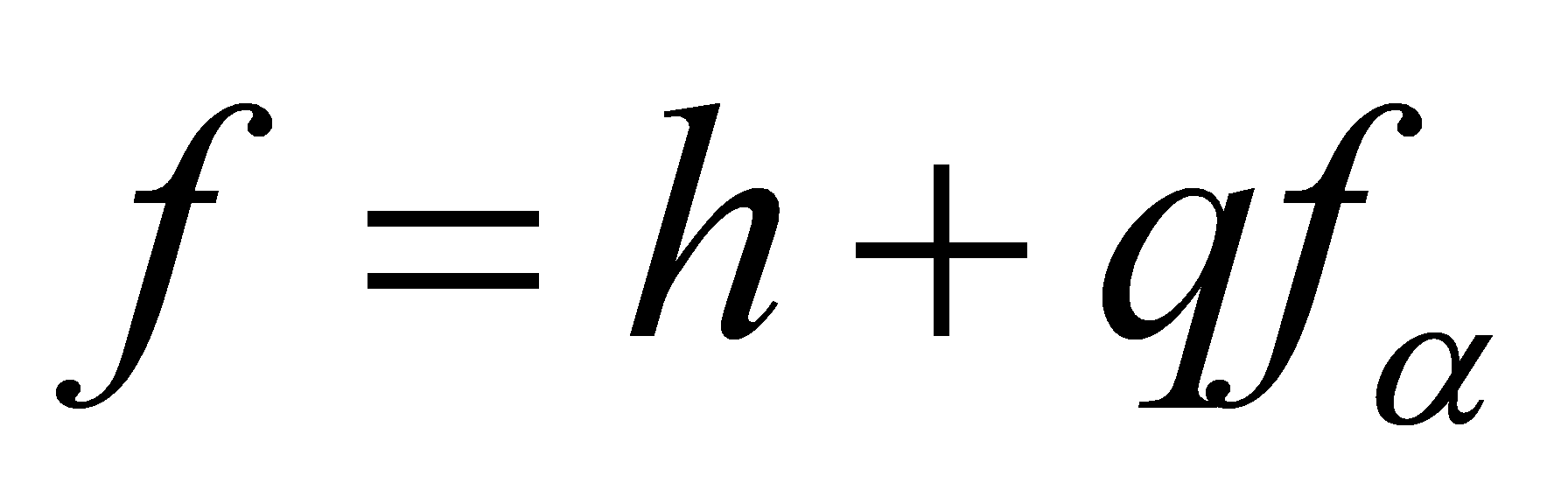 where
where . Since
. Since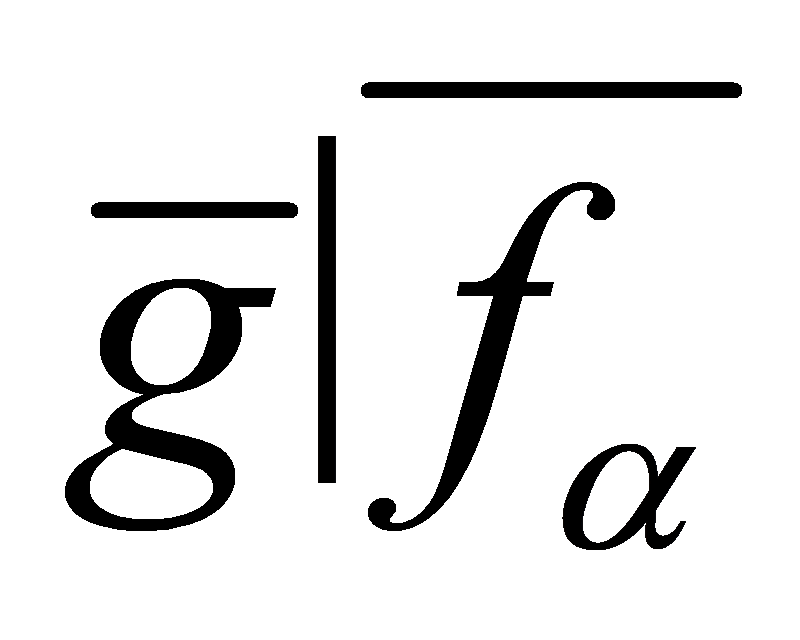 , then
, then , thus
, thus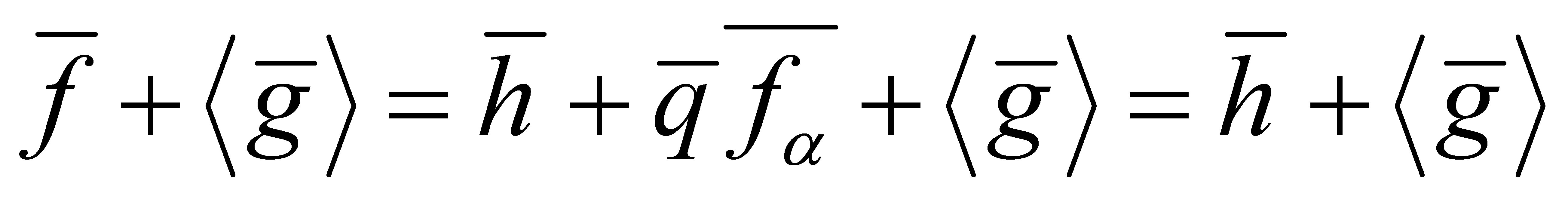 and
and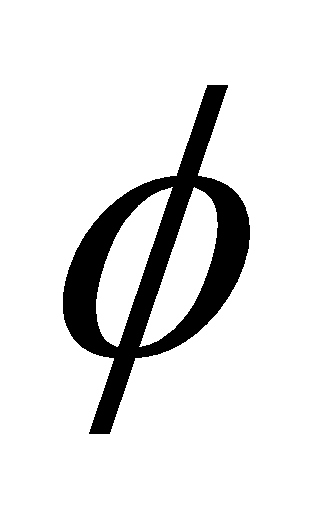 is well defined. It is clearly a ring homomorphism and subjective. Consider the ideal
is well defined. It is clearly a ring homomorphism and subjective. Consider the ideal of
of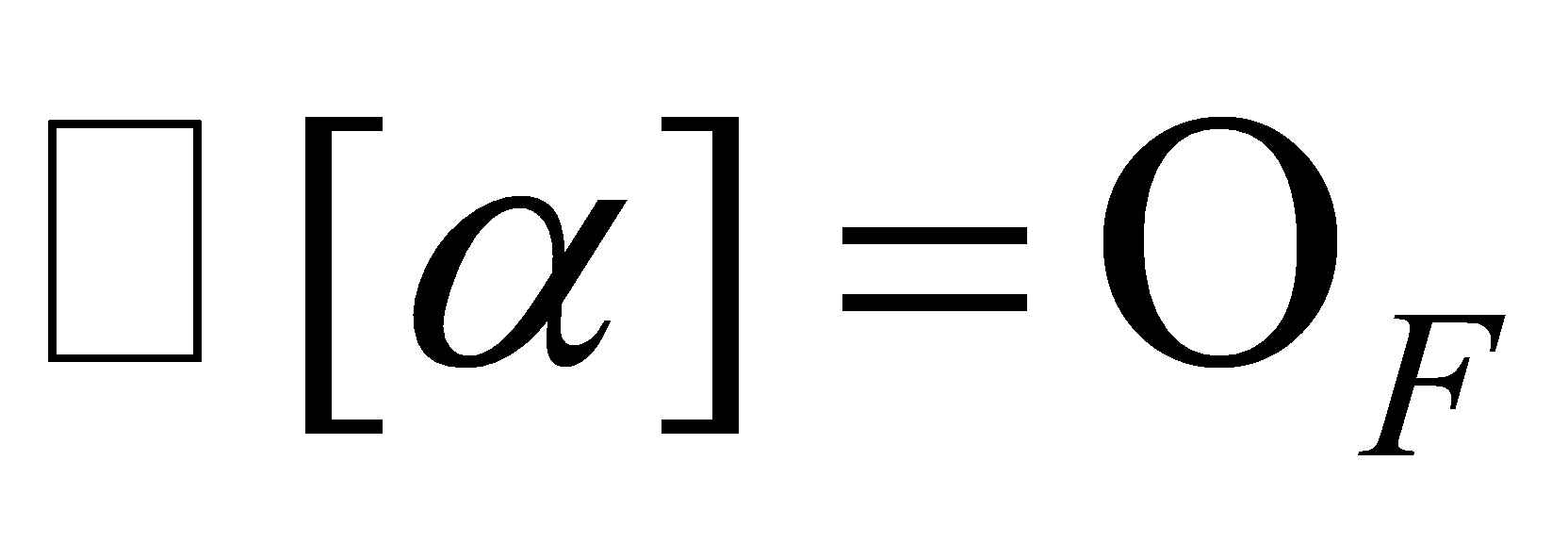 . By the First Isomorphism Theorem,
. By the First Isomorphism Theorem,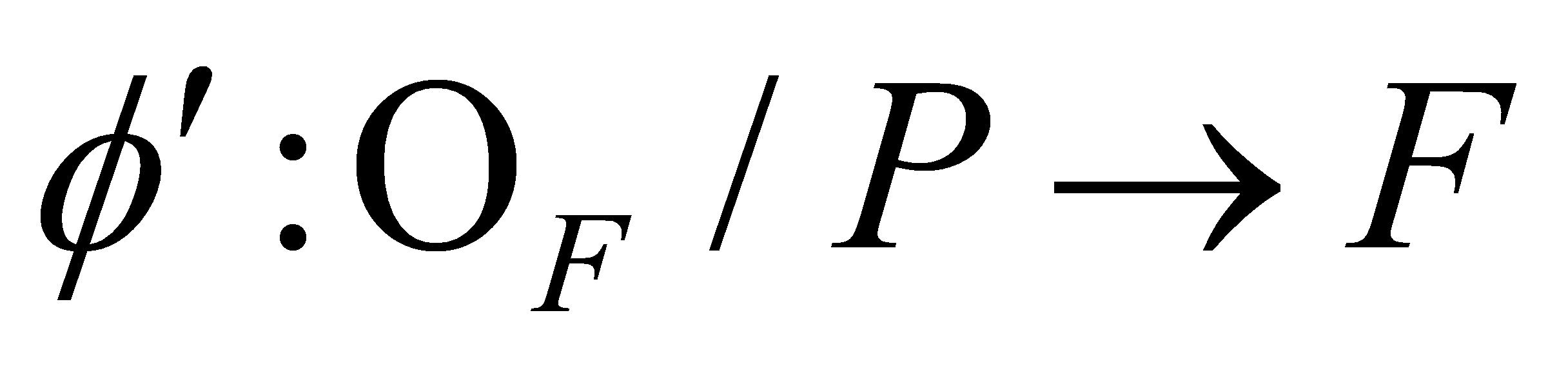 is an isomorphism, then
is an isomorphism, then 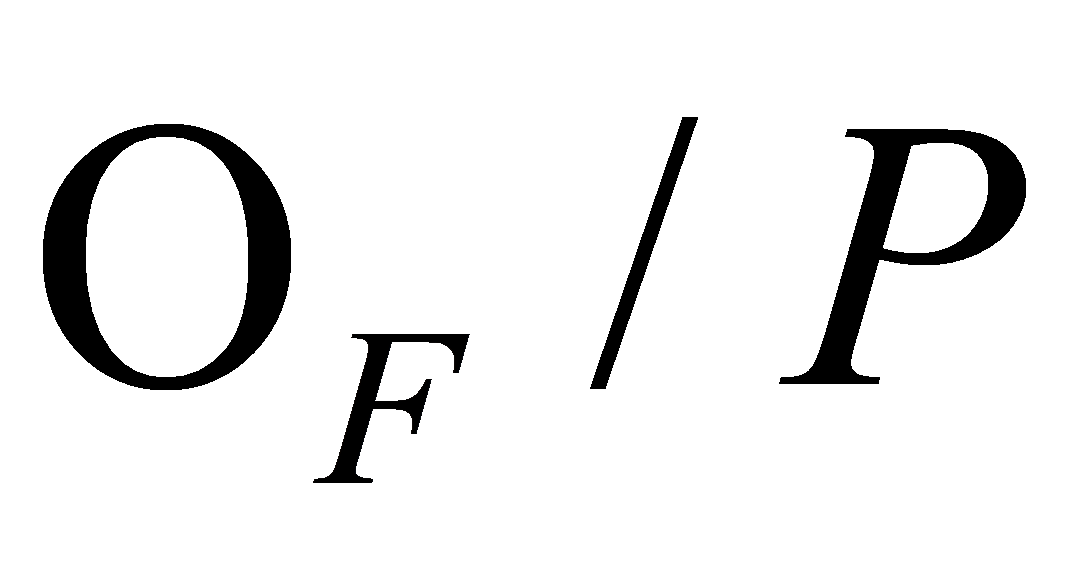 is a field with
is a field with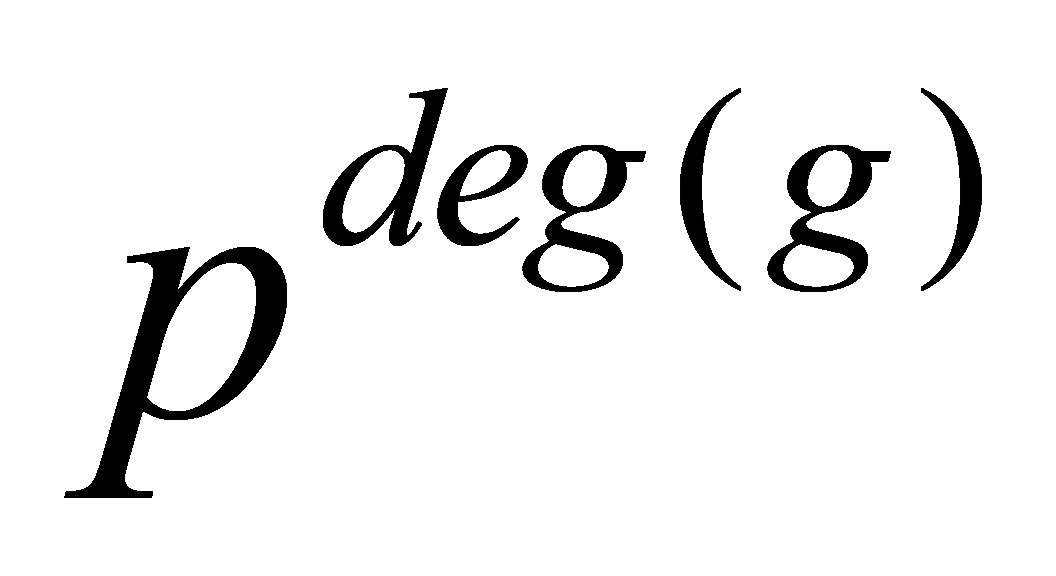 elements. Therefore,
elements. Therefore,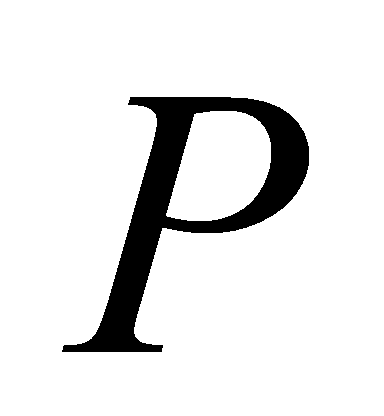 is a maximal ideal of
is a maximal ideal of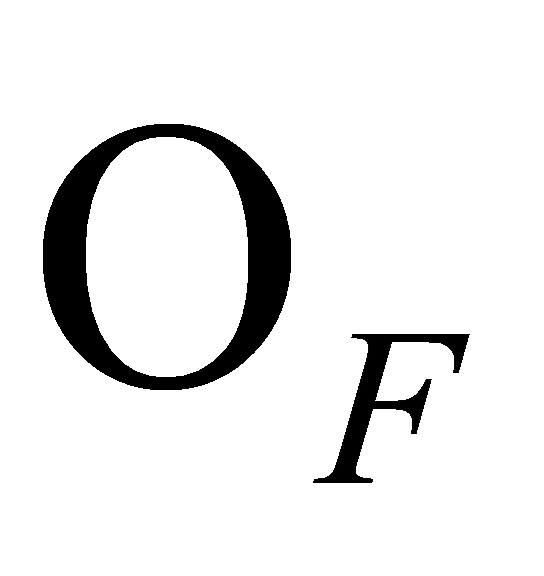 and a prime ideal with
and a prime ideal with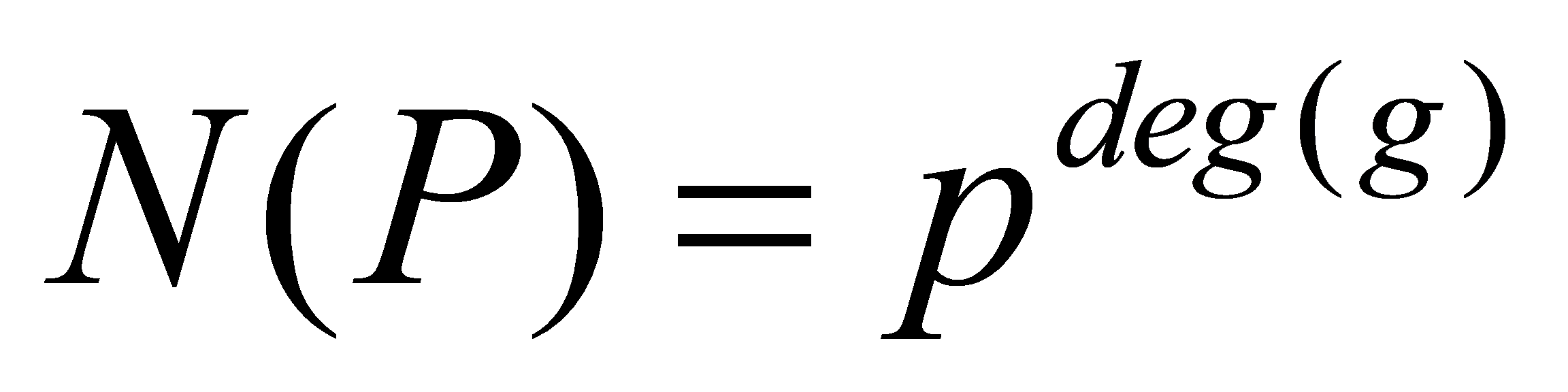 .
.
We just need to show that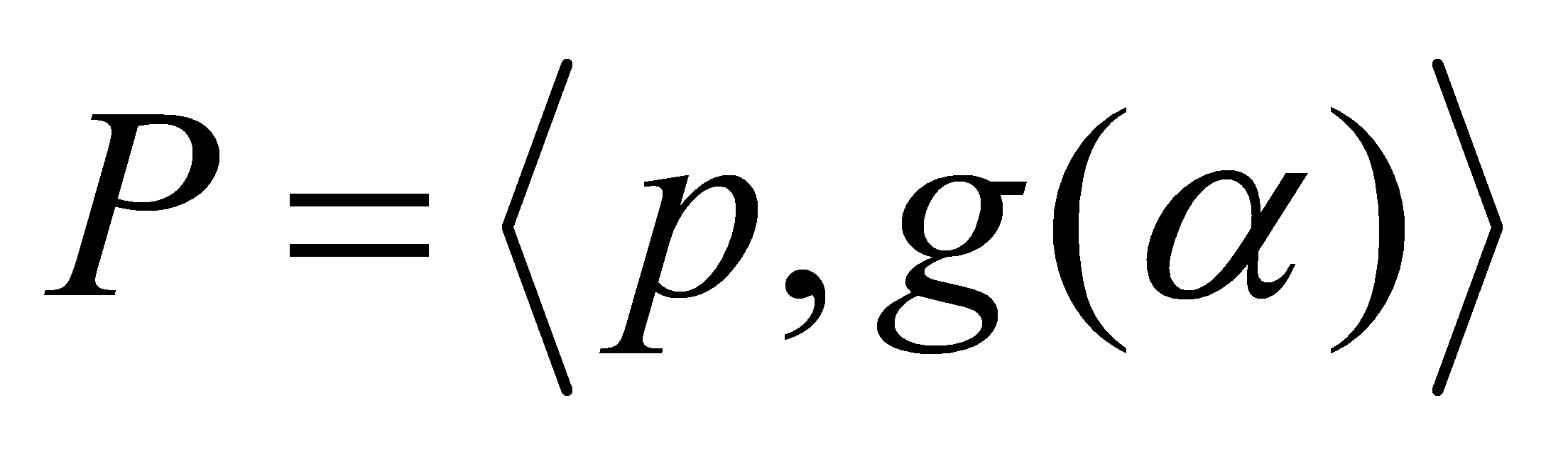 . First, since
. First, since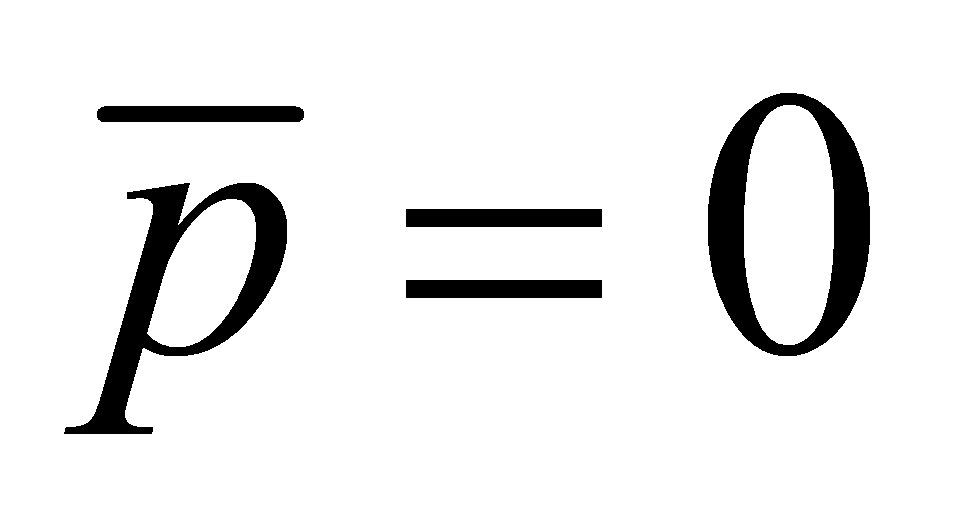 , we have
, we have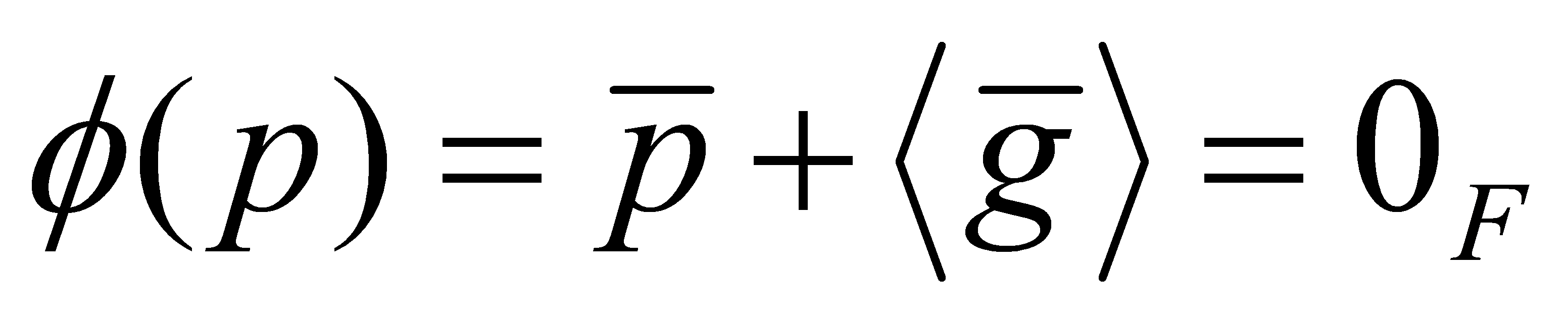 . Moreover,
. Moreover,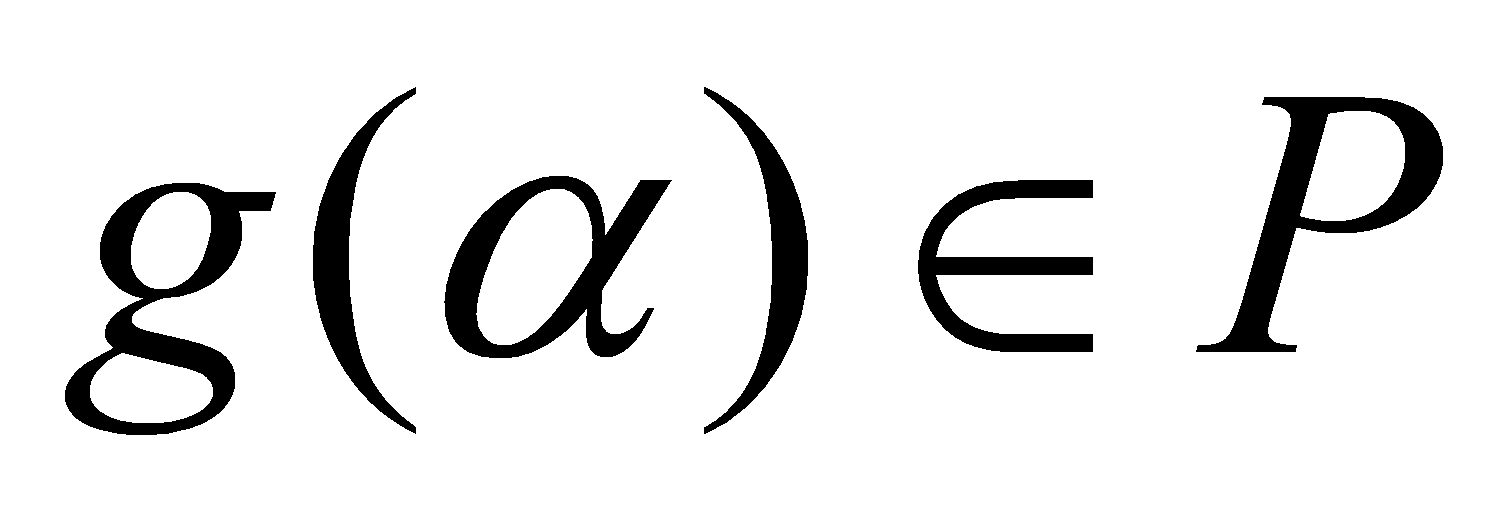 , as
, as . Thus
. Thus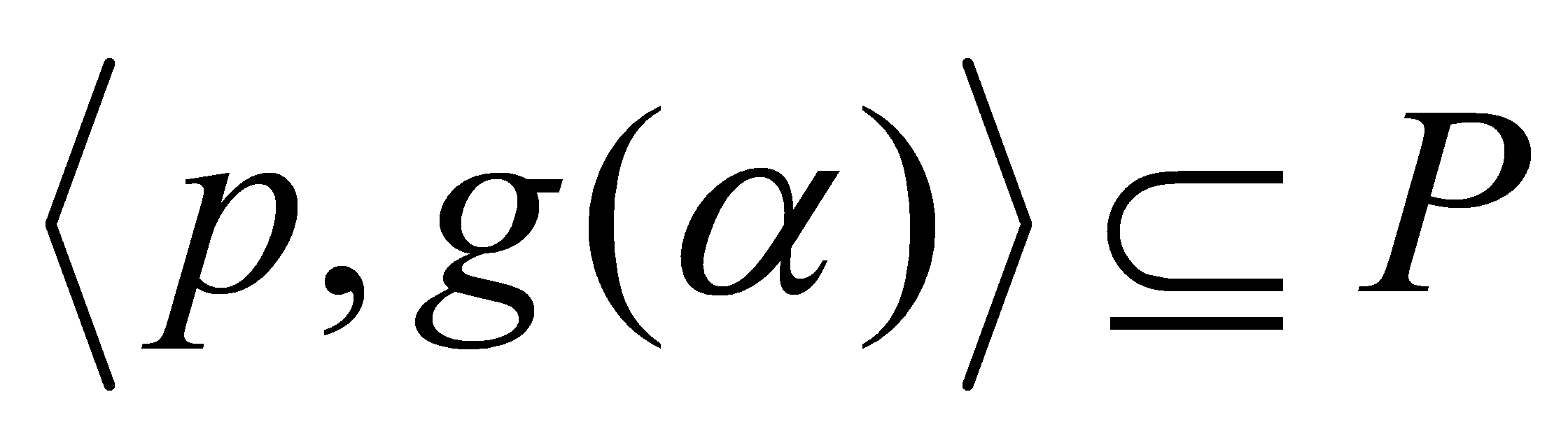 . Conversely, let
. Conversely, let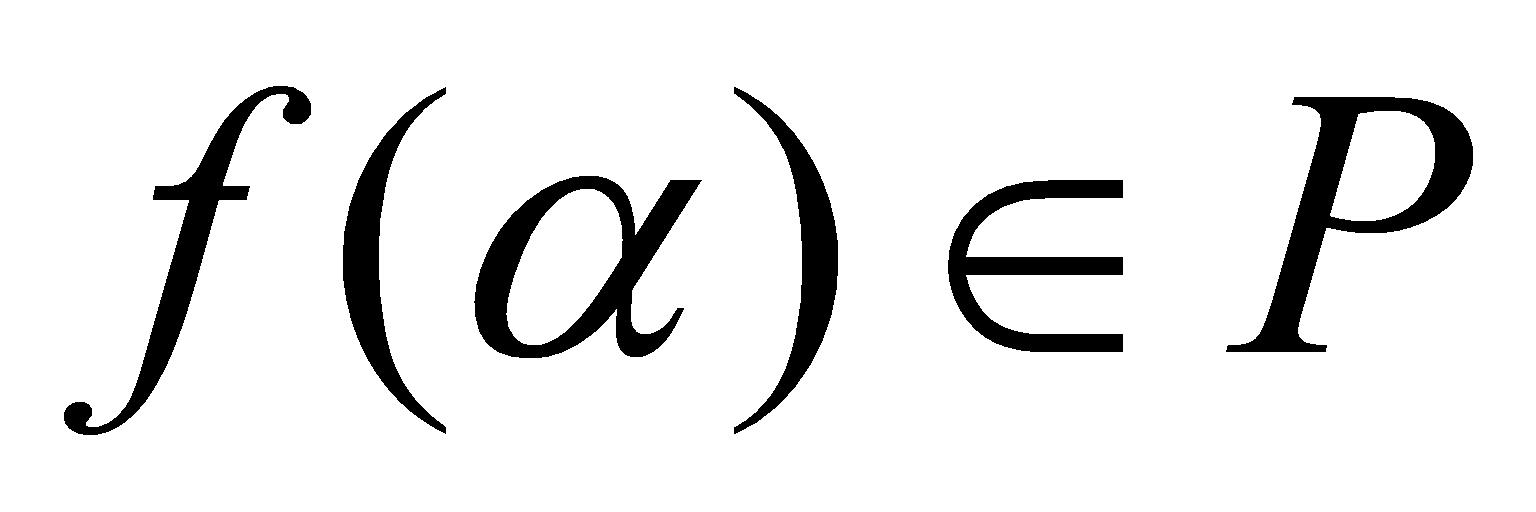 . Then
. Then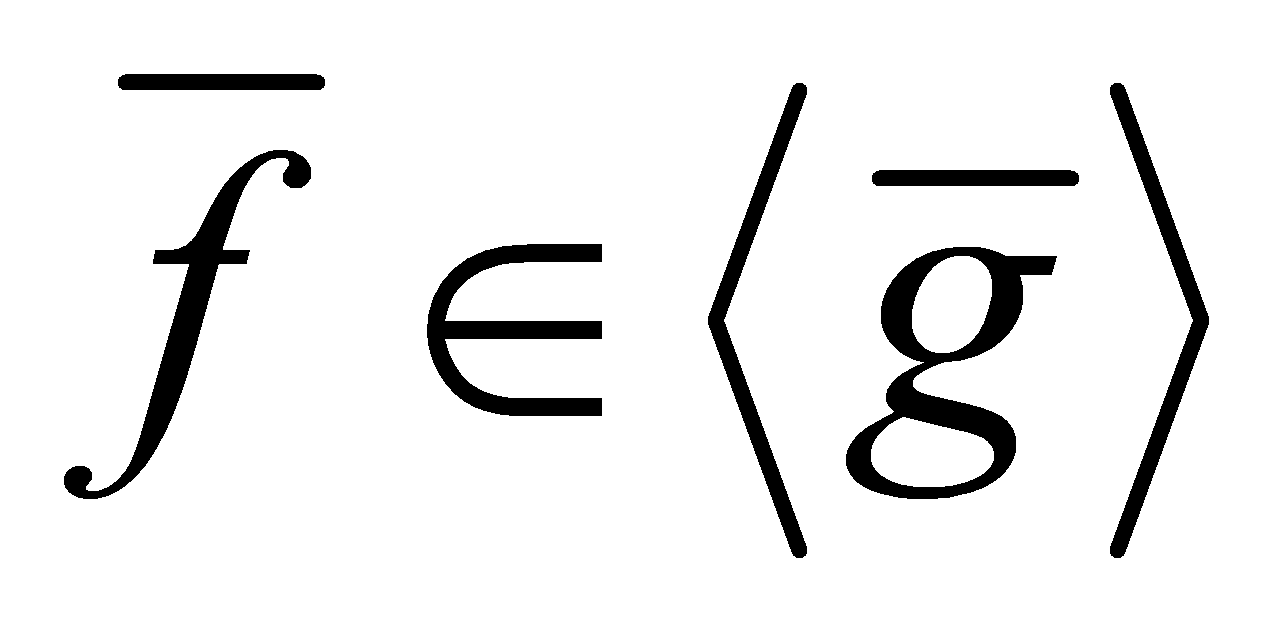 , so
, so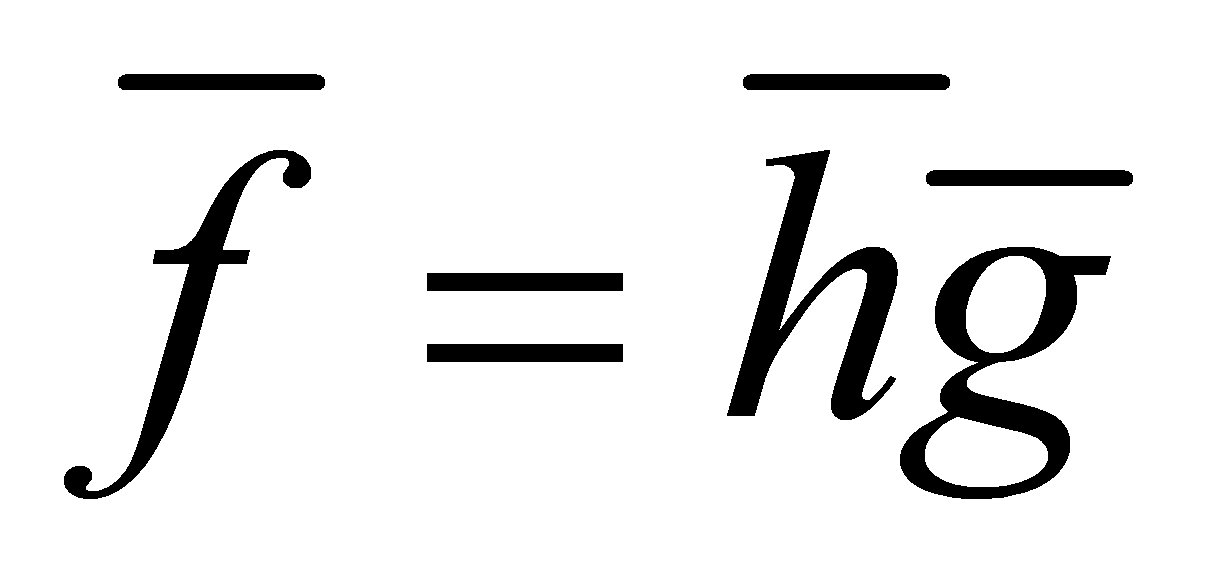 , for some
, for some . Then the polynomials
. Then the polynomials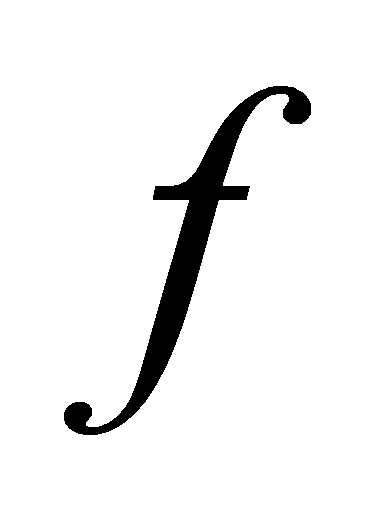 and
and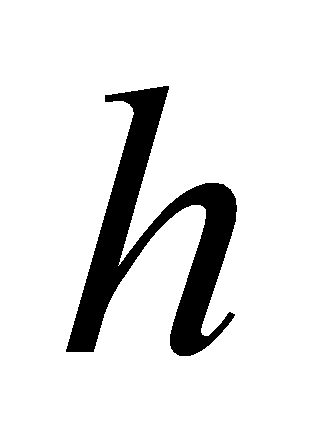
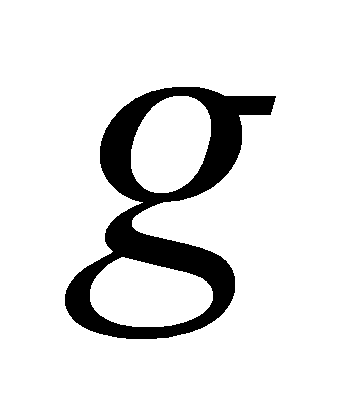 are congruent modulo
are congruent modulo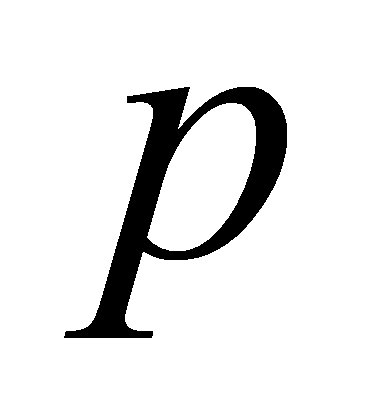 , so all coefficients of
, so all coefficients of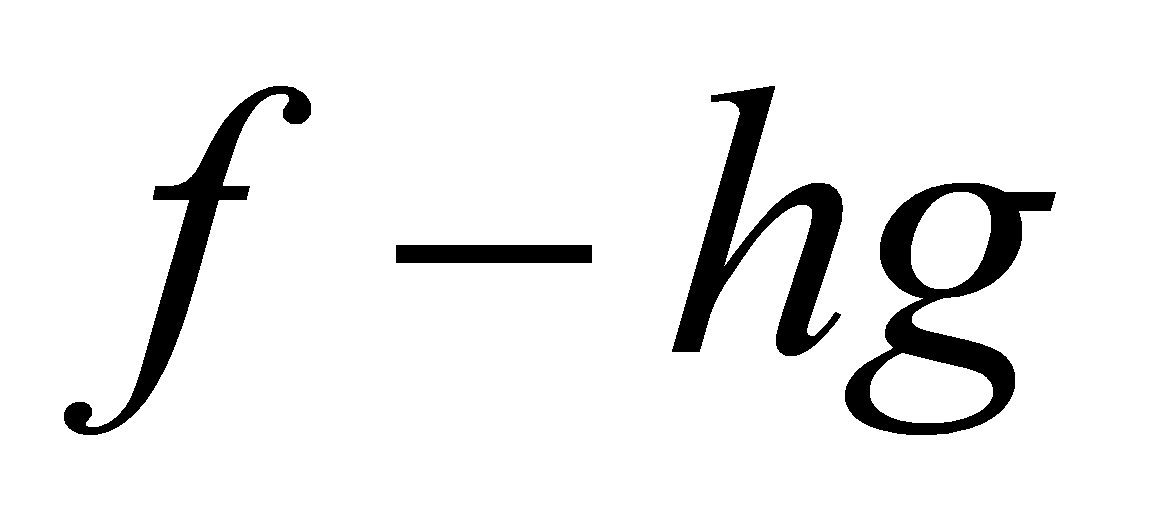 are divisible by
are divisible by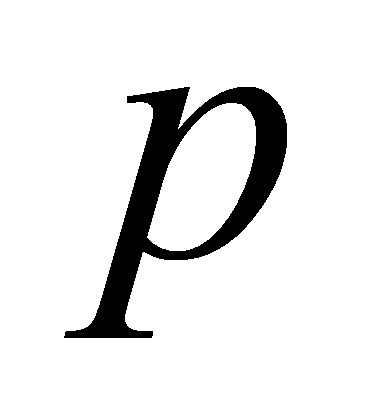 . Hence, there is a polynomial
. Hence, there is a polynomial , such that
, such that . Plugging in
. Plugging in ,
,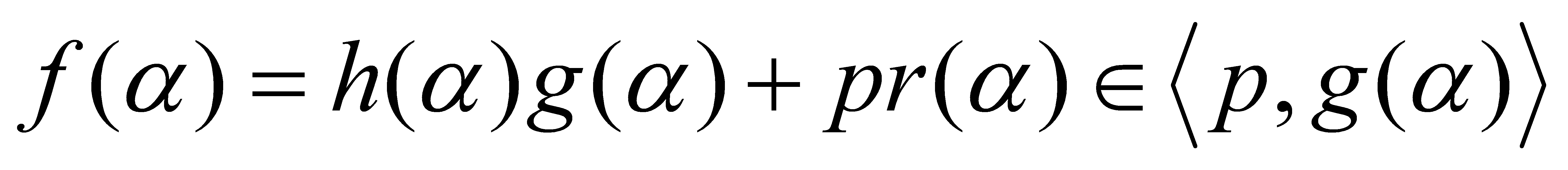 is obtained. Thus
is obtained. Thus . Since
. Since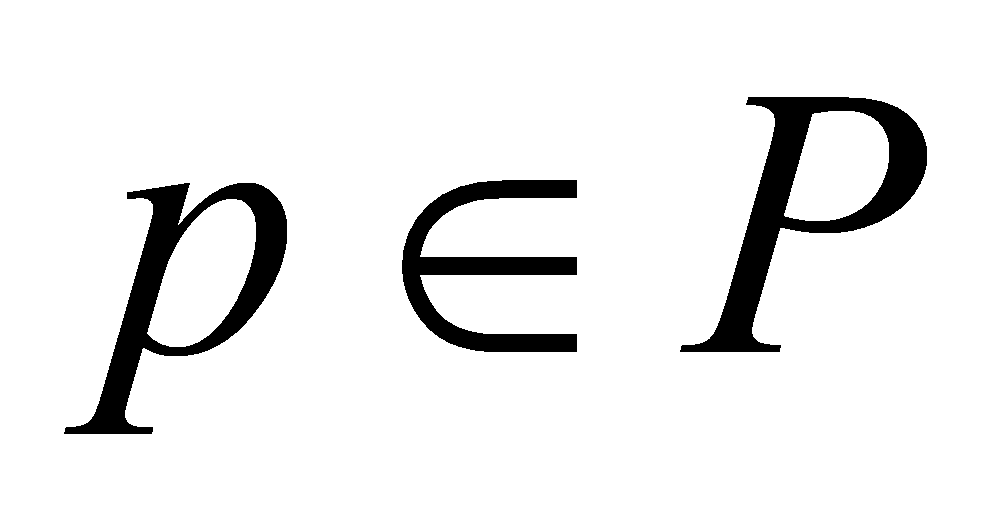 , we have
, we have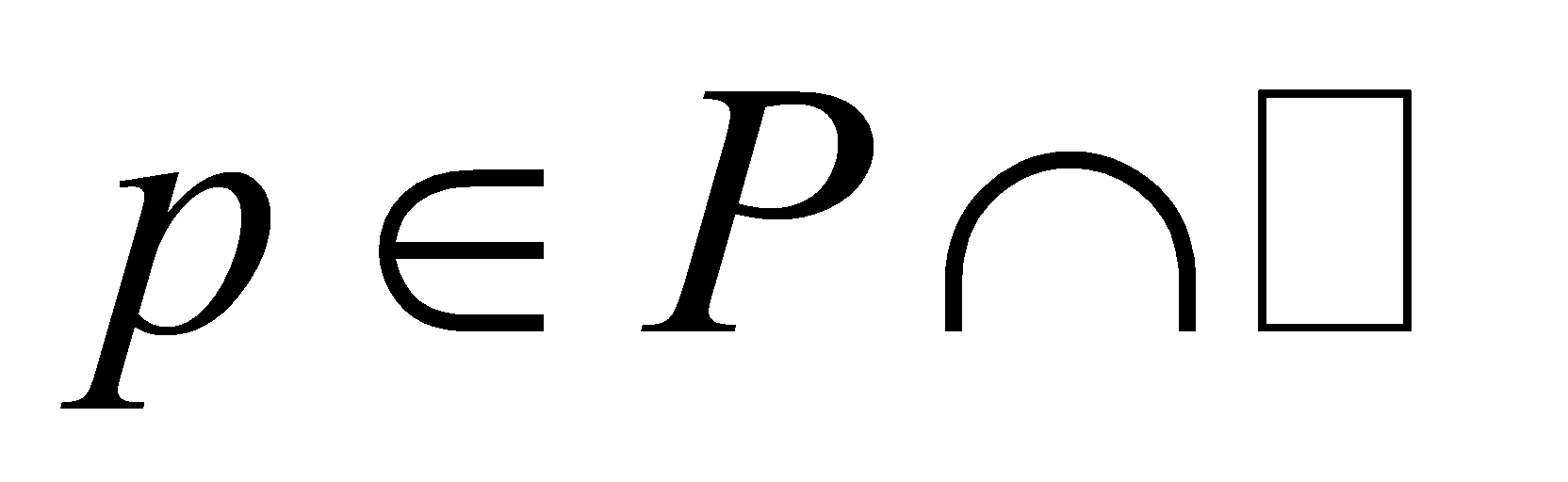 . By Lemma 2.5,
. By Lemma 2.5,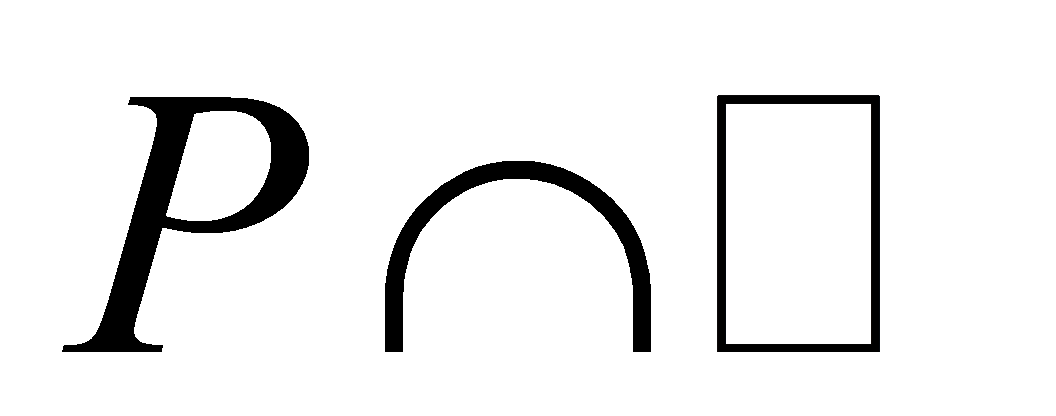 is a prime ideal of
is a prime ideal of that contains
that contains , thus
, thus . By Lemma 2.7, it shows that
. By Lemma 2.7, it shows that lies above
lies above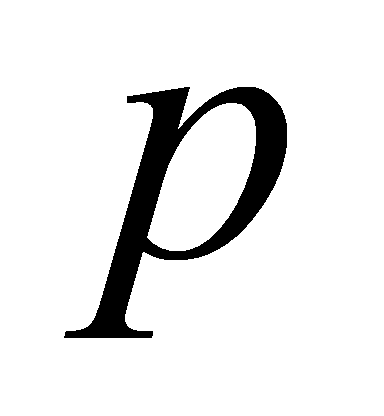 .
.
2.3. Factoring prime
Theorem 2.9. Let be a number field and assume that
be a number field and assume that for some
for some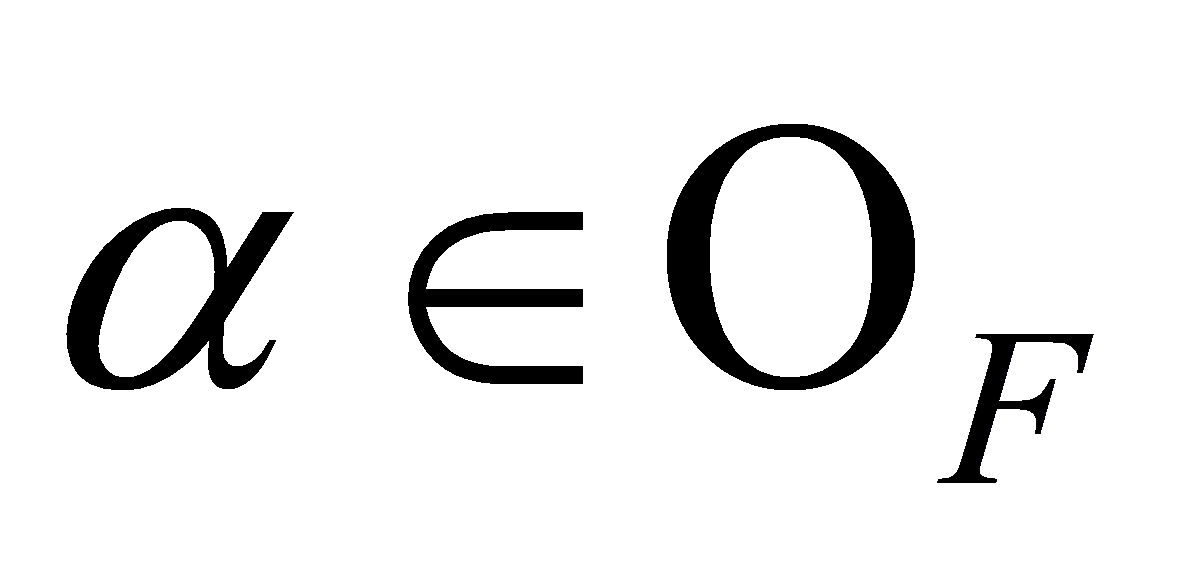 . Let
. Let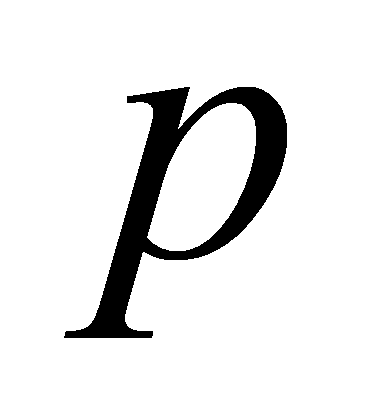 be prime and
be prime and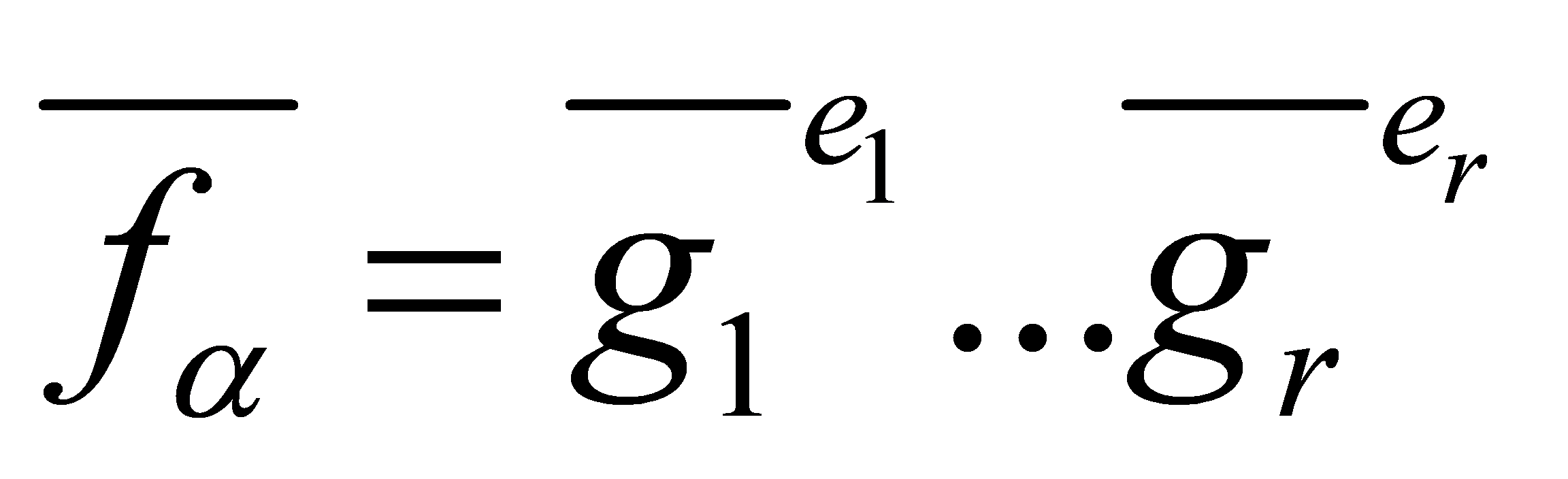 be the factorization of
be the factorization of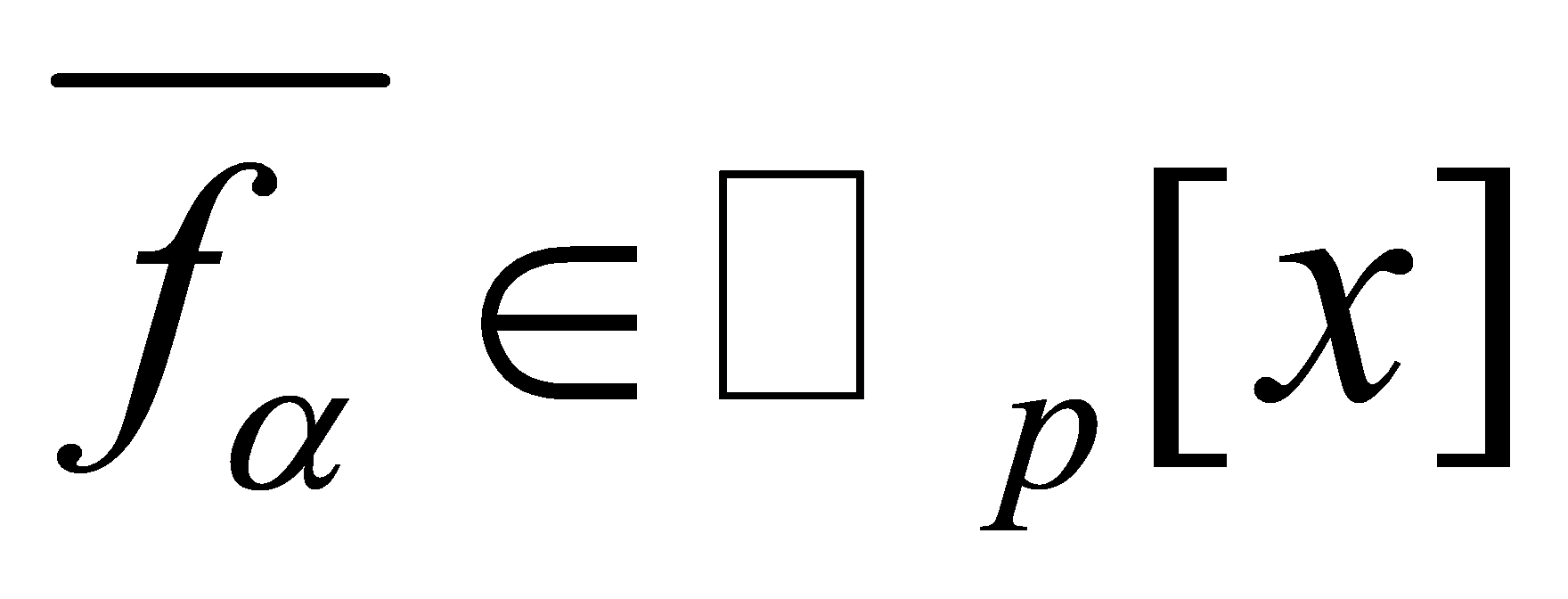 [7] into irreducibles. That is,
[7] into irreducibles. That is, are monic polynomials, such that the
are monic polynomials, such that the are distinct and irreducible in
are distinct and irreducible in , and
, and . Then the prime ideals of
. Then the prime ideals of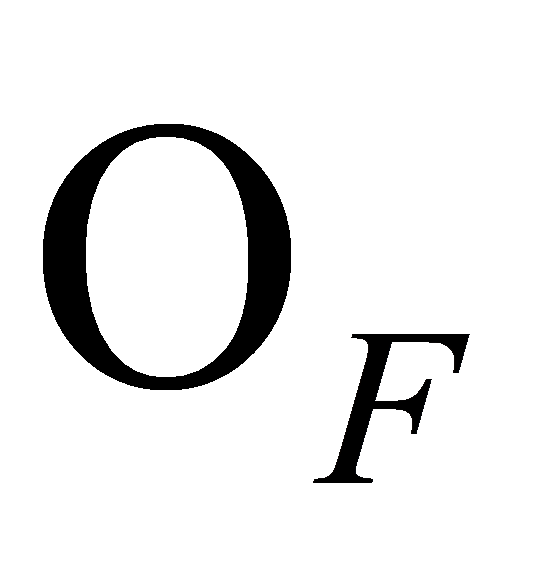 lying above
lying above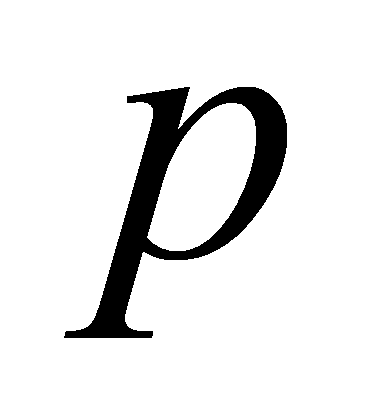 are precisely the ideals
are precisely the ideals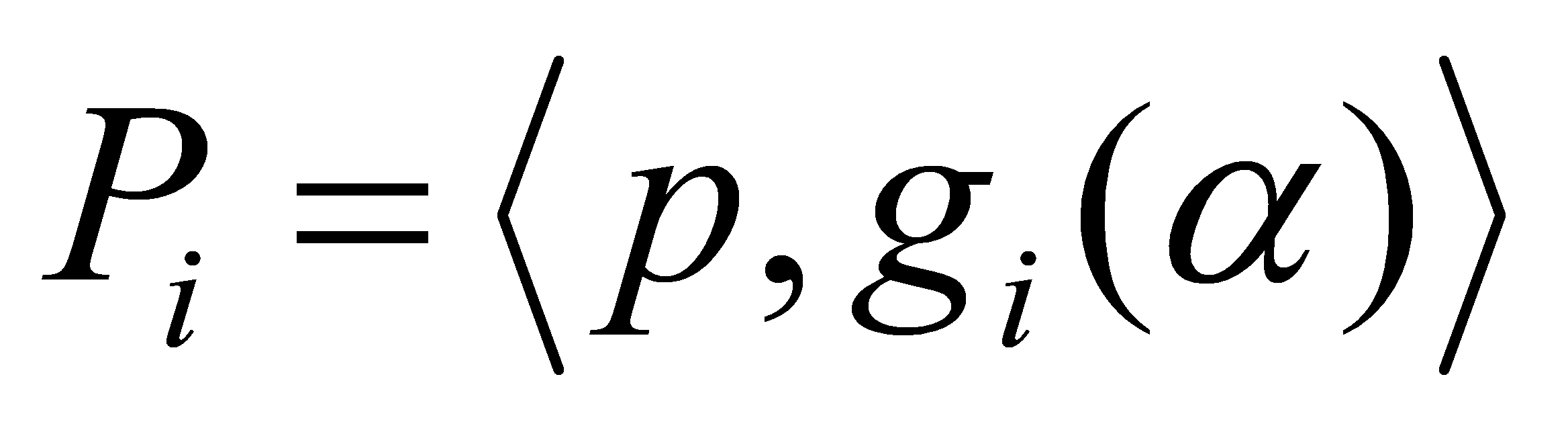 , for
, for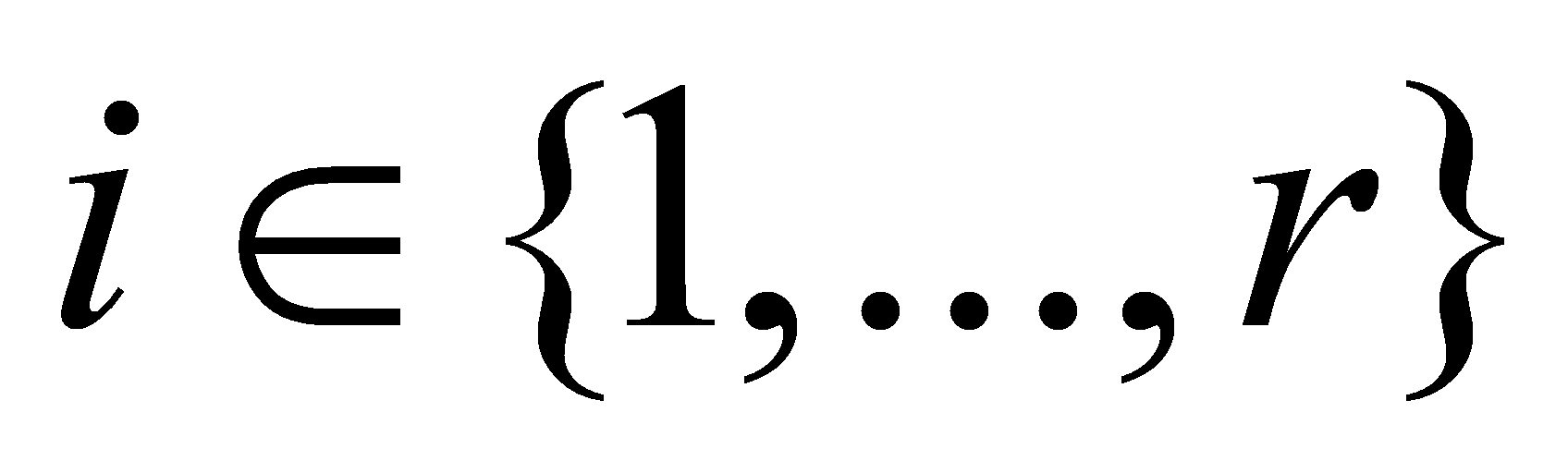 . The ideal
. The ideal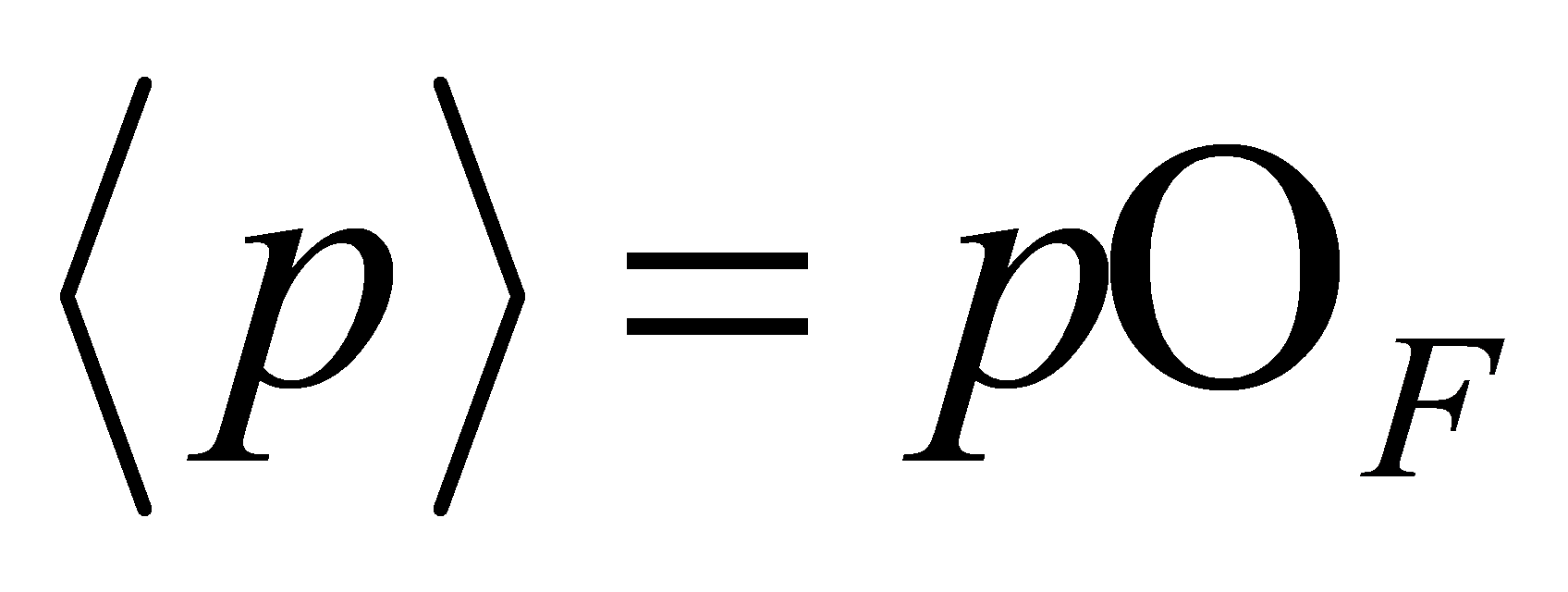 of
of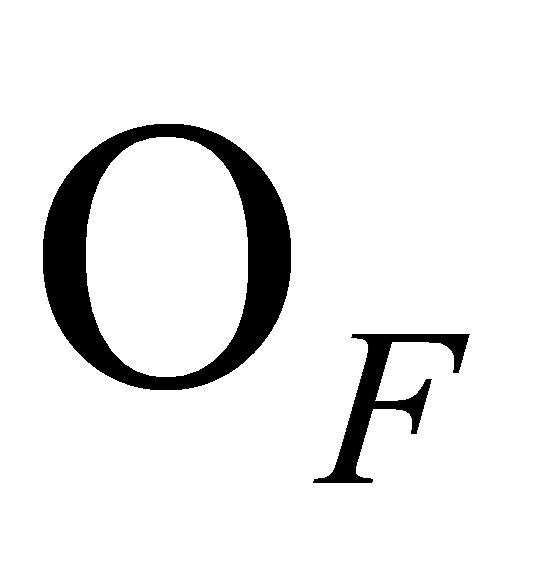 factorises into prime ideals as
factorises into prime ideals as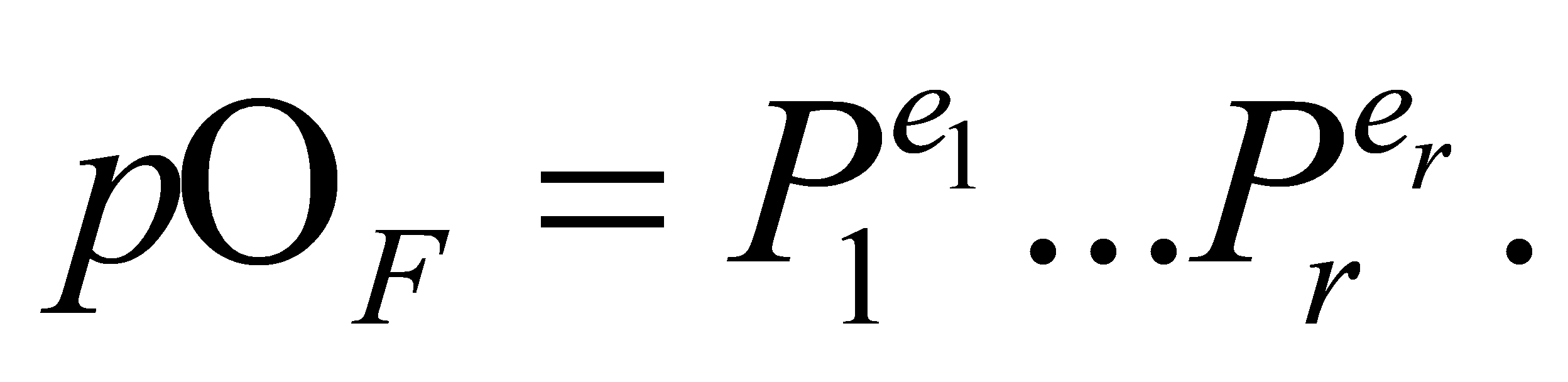
Proof. It is known from Theorem 2.8 that all are prime ideals with
are prime ideals with , where
, where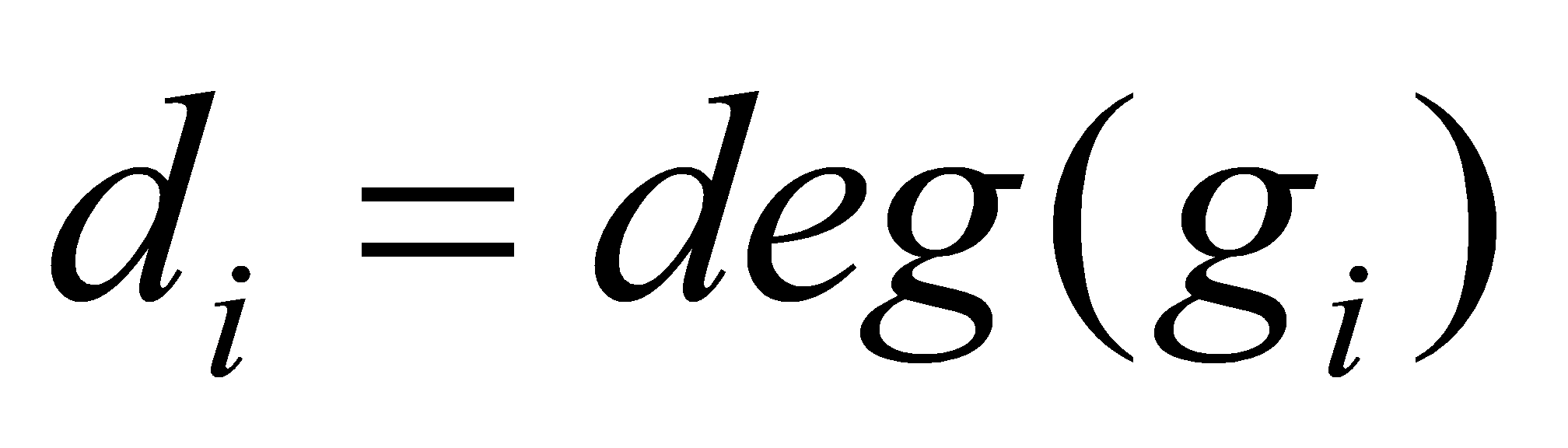 . From the factorization
. From the factorization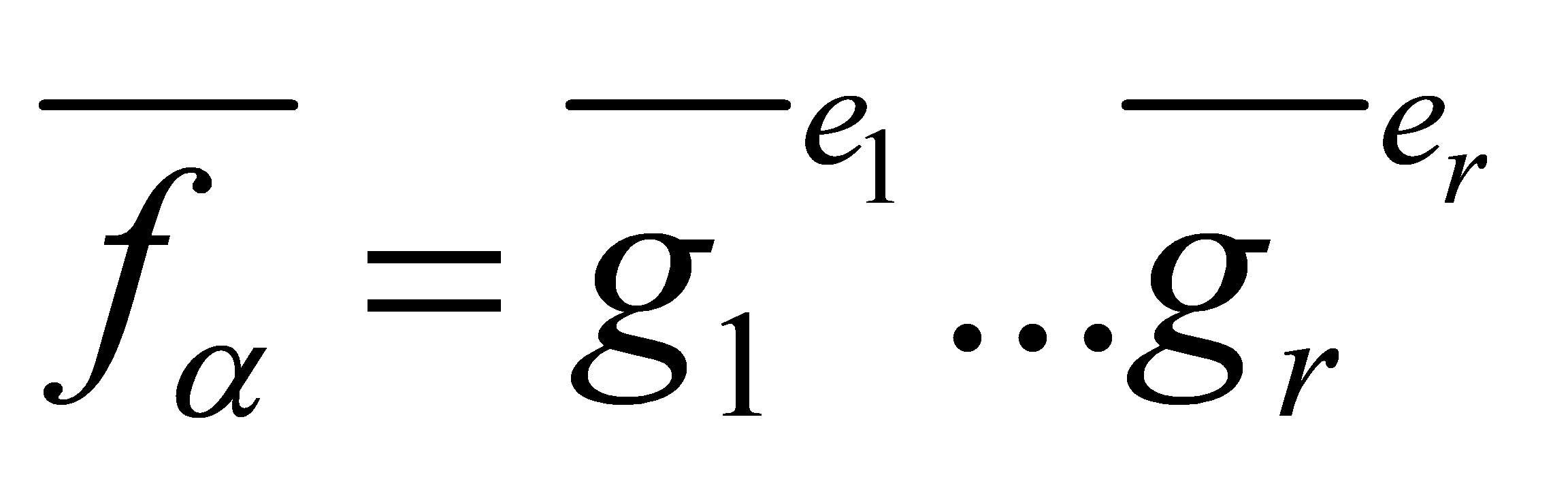 , it can get
, it can get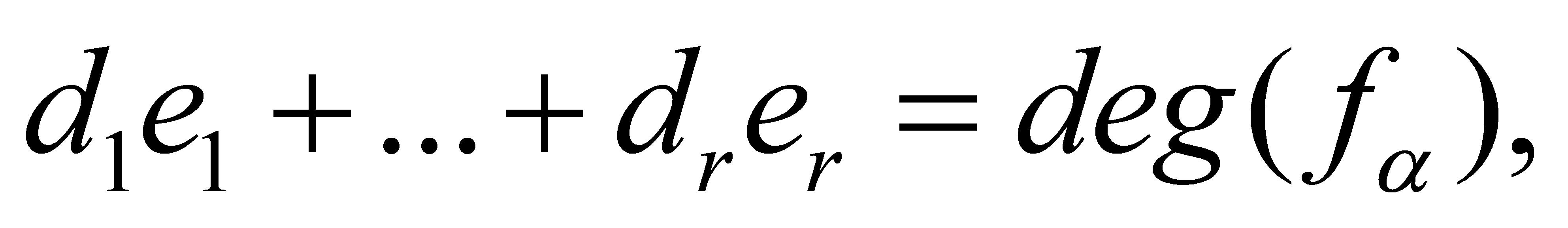 since all
since all are monic,
are monic, . For arbitrary ideals
. For arbitrary ideals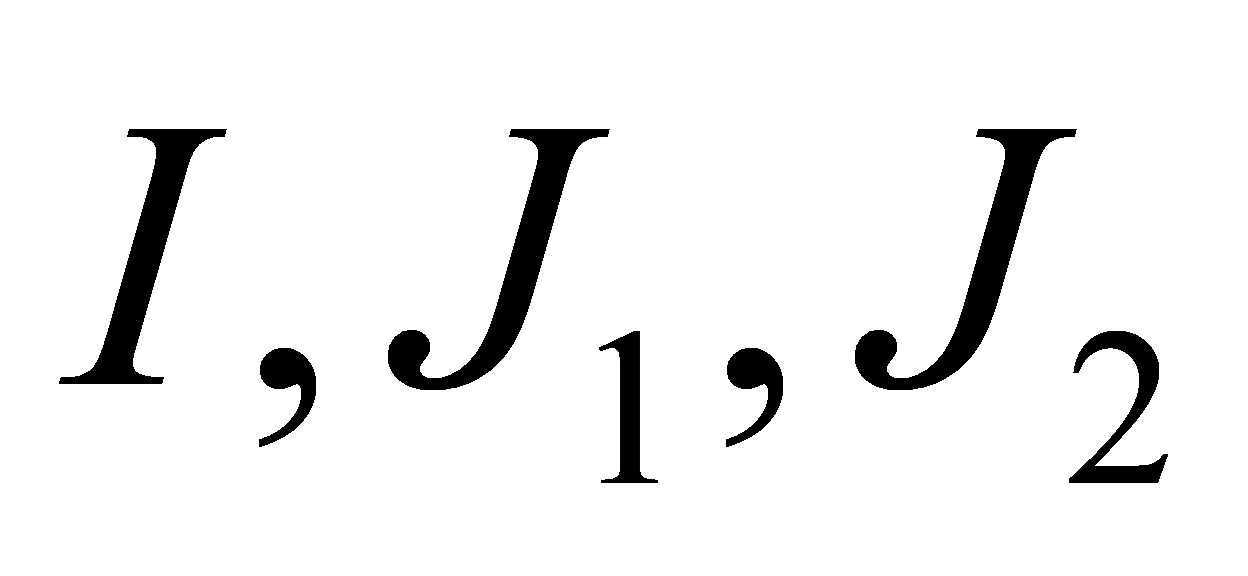 of
of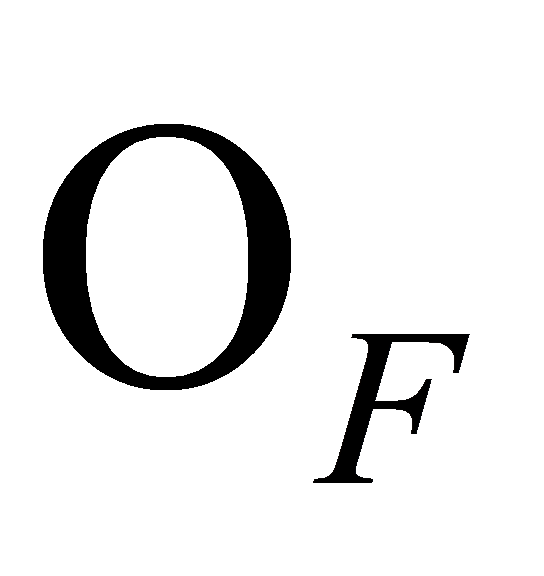 , Equation (1) is obtained:
, Equation (1) is obtained:
 (1)
(1)
Applying this inductively to the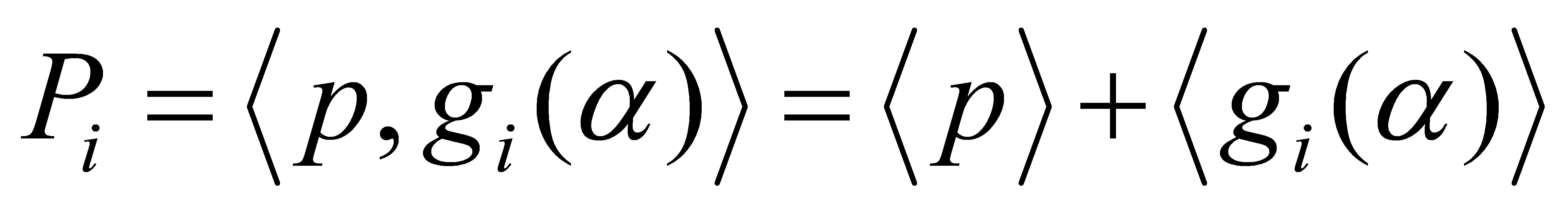 , Equation (2) is obtained:
, Equation (2) is obtained:
 (2)
(2)
The last equality holds due to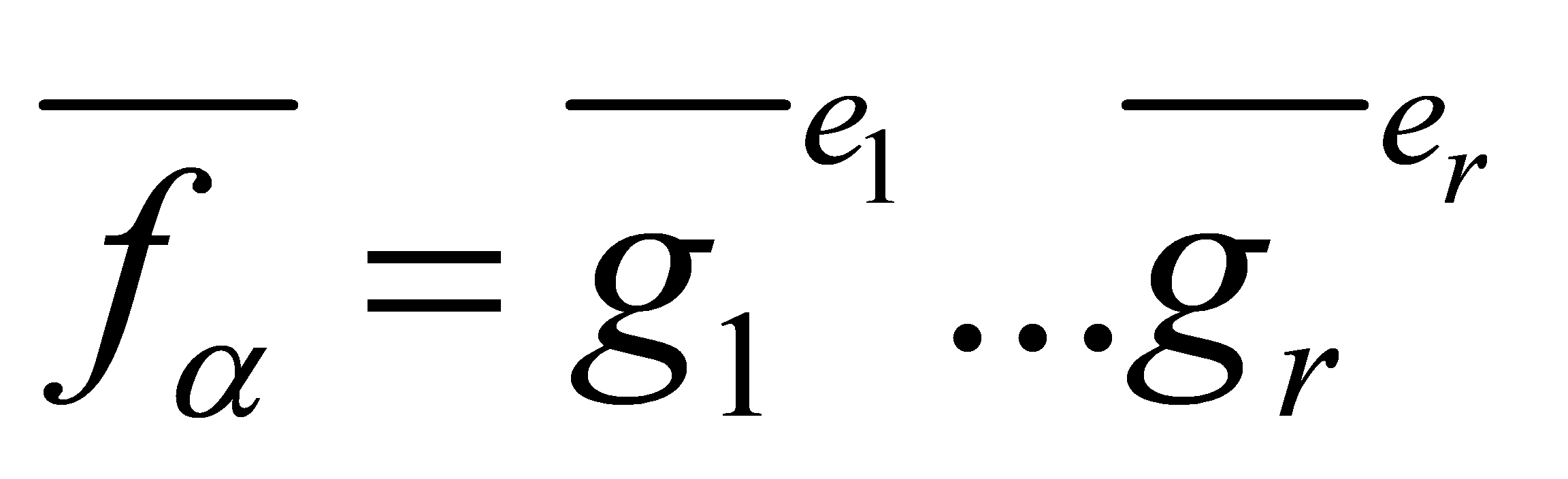 , as then
, as then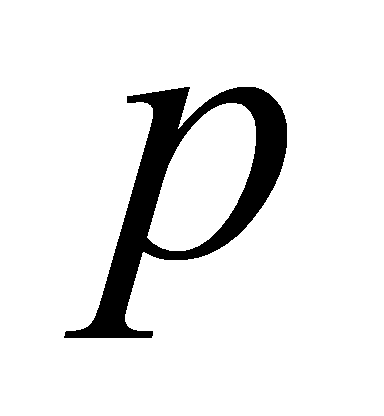 divides all coefficients of
divides all coefficients of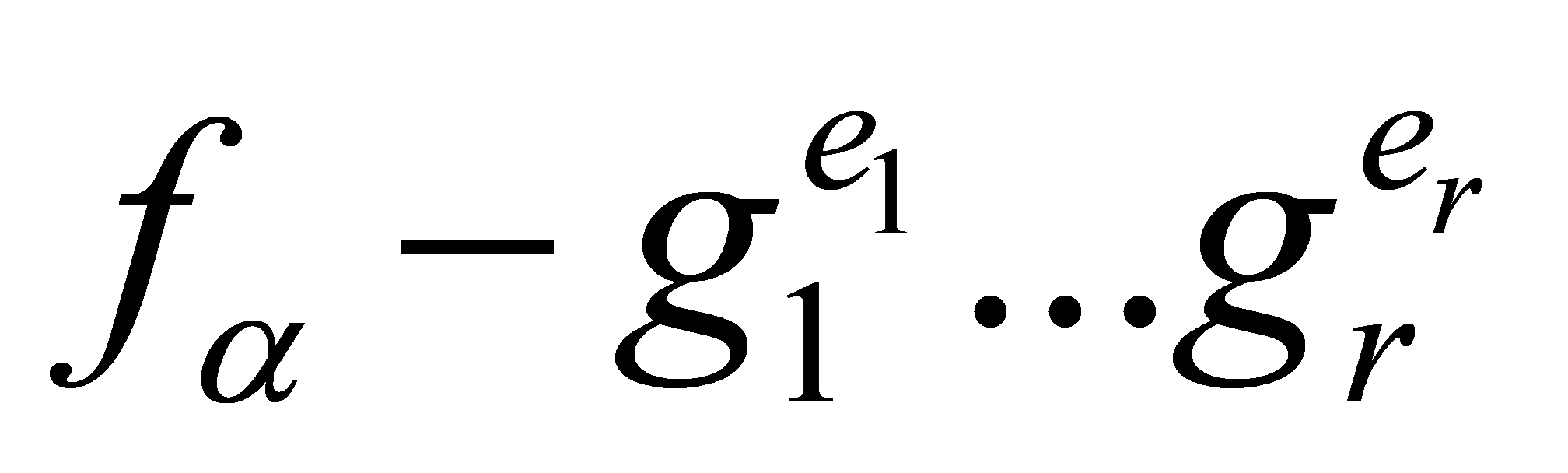 , so
, so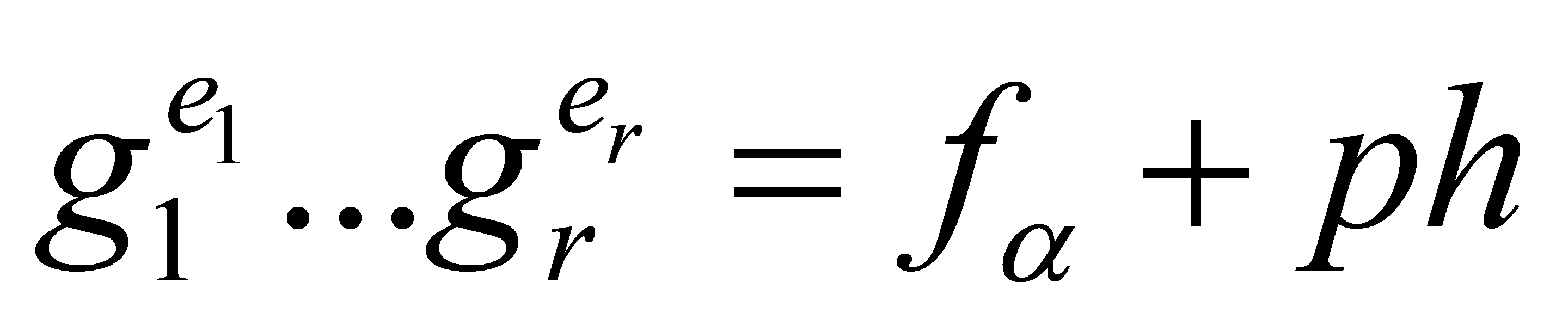 , for some
, for some . But then
. But then .
.
Thus,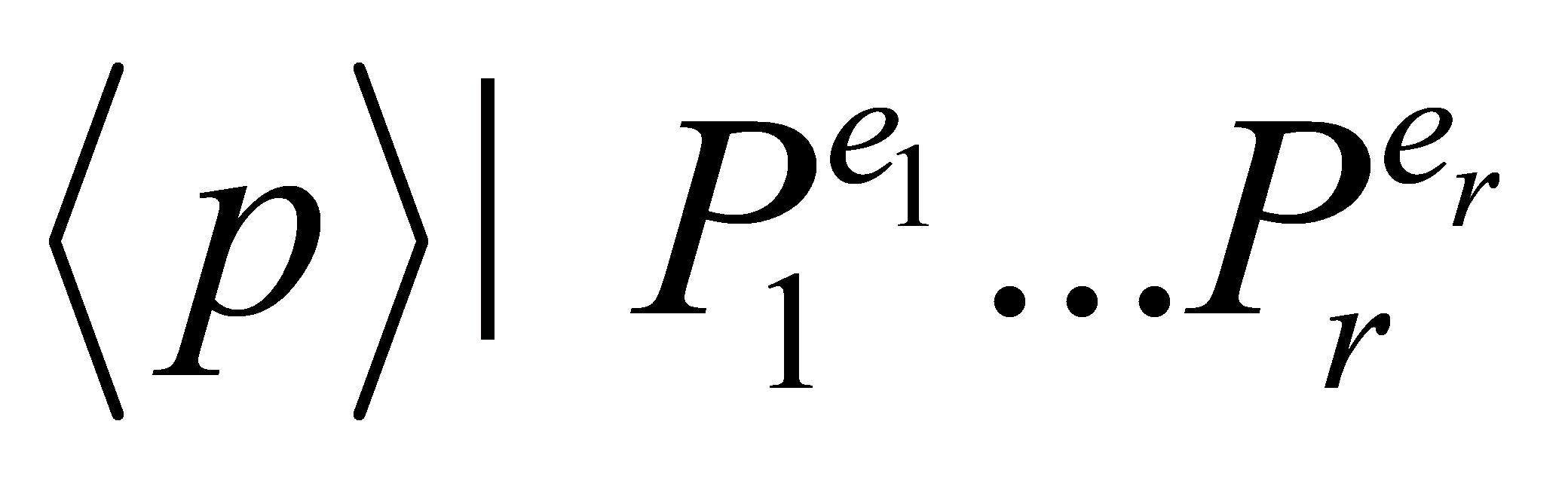 is obtained and hence
is obtained and hence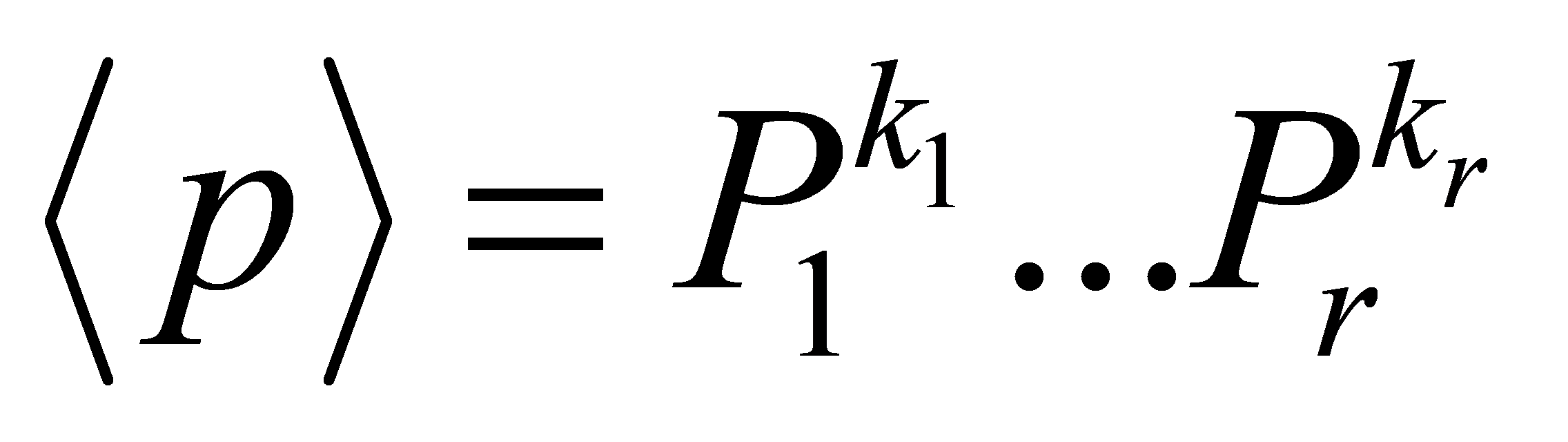 with
with . Hence, the
. Hence, the is indeed the only prime ideals of
is indeed the only prime ideals of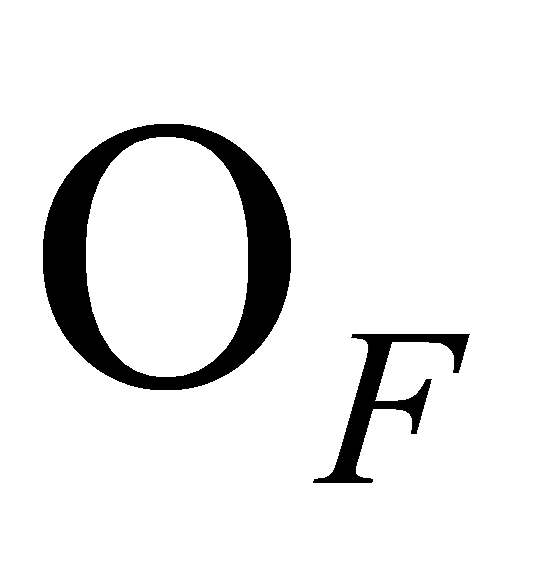 lying above
lying above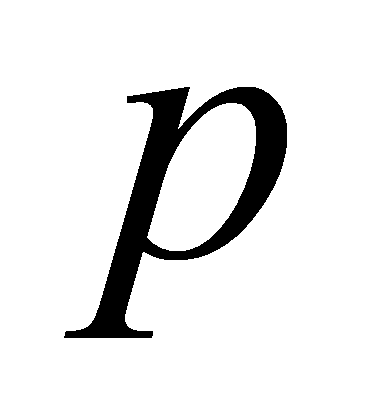 . Moreover, Equation (3) is obtained:
. Moreover, Equation (3) is obtained:
 (3)
(3)
Compare this to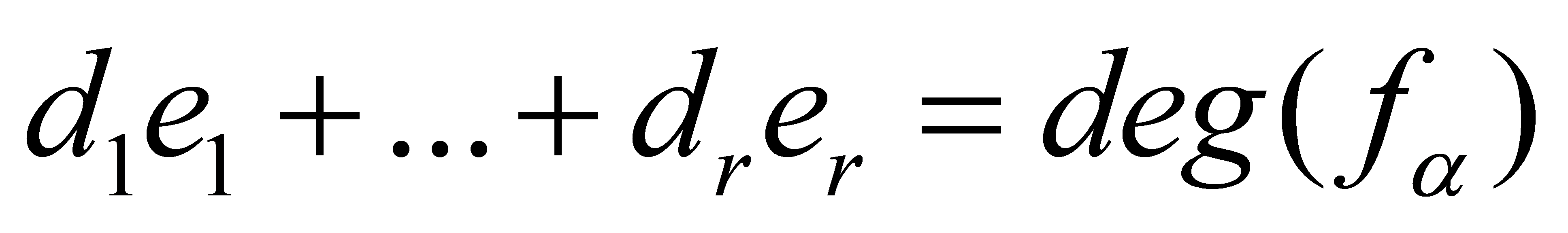 to conclude that
to conclude that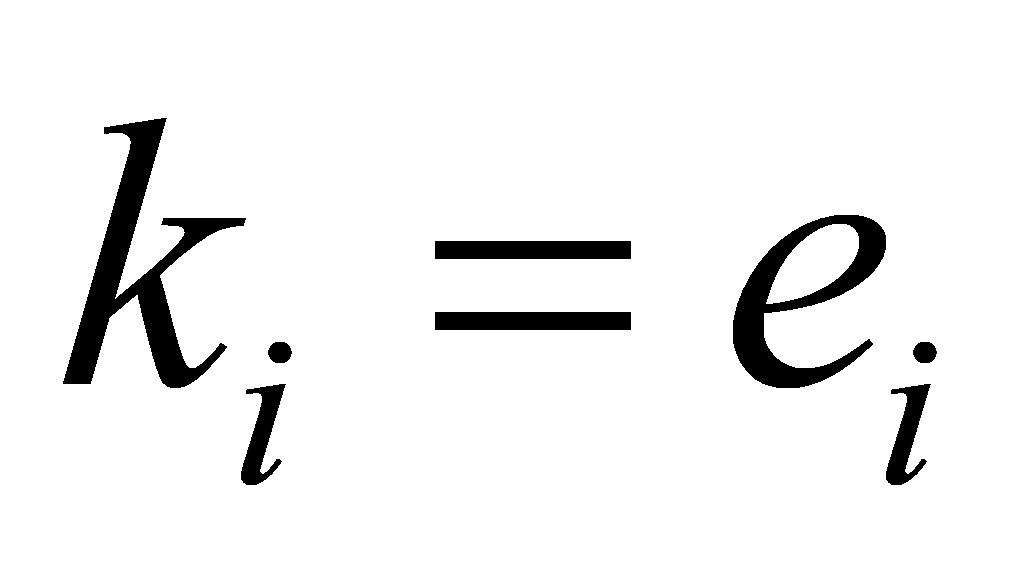 for all
for all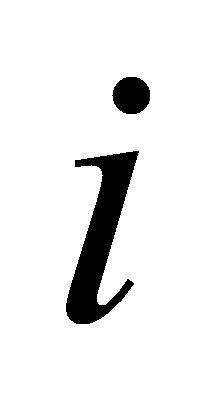 .
.
3. Primes as sums of two squares
Lemma 3.1. Let be an odd prime, such that
be an odd prime, such that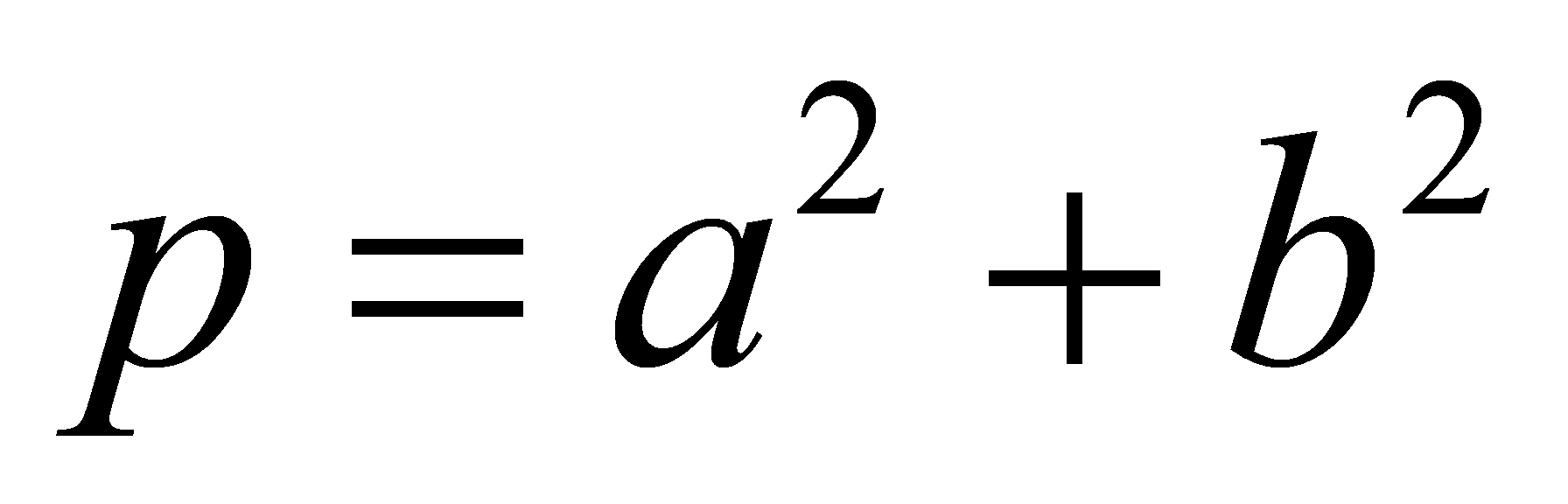 , with
, with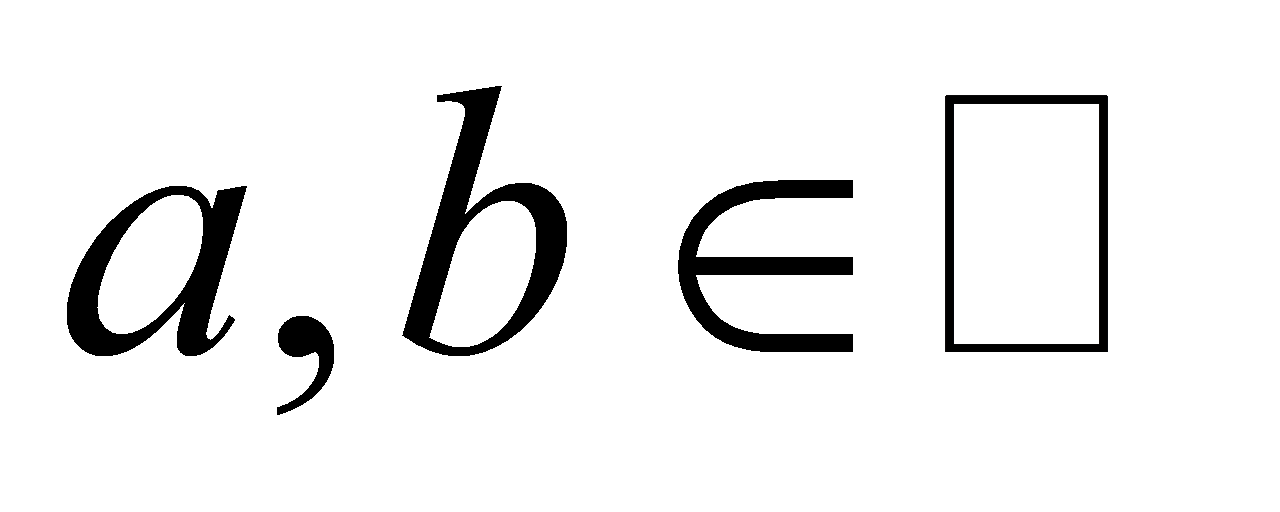 . Then
. Then 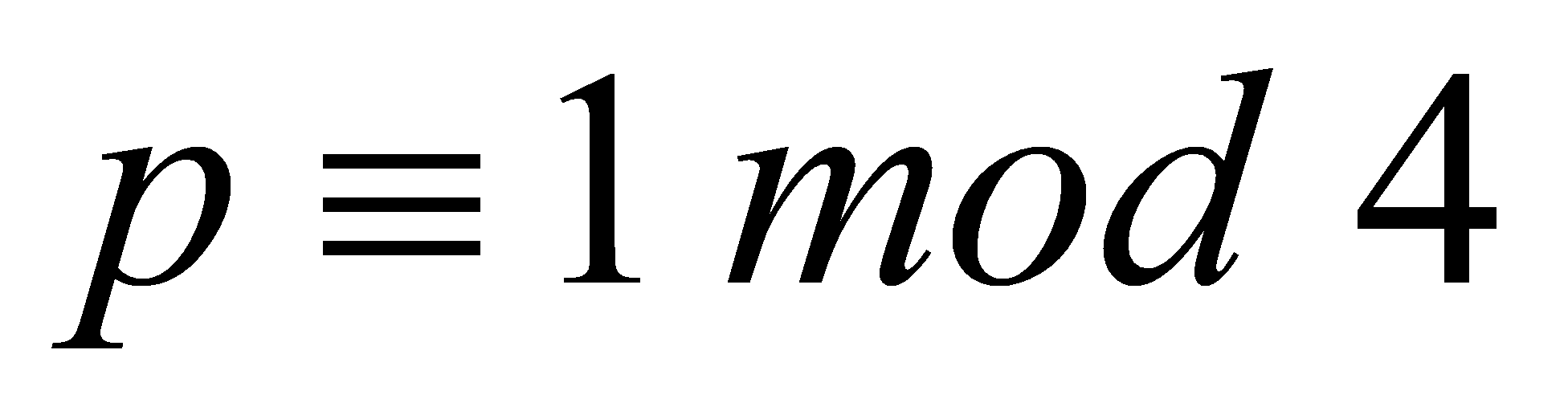 .
.
Proof. Since ,
, 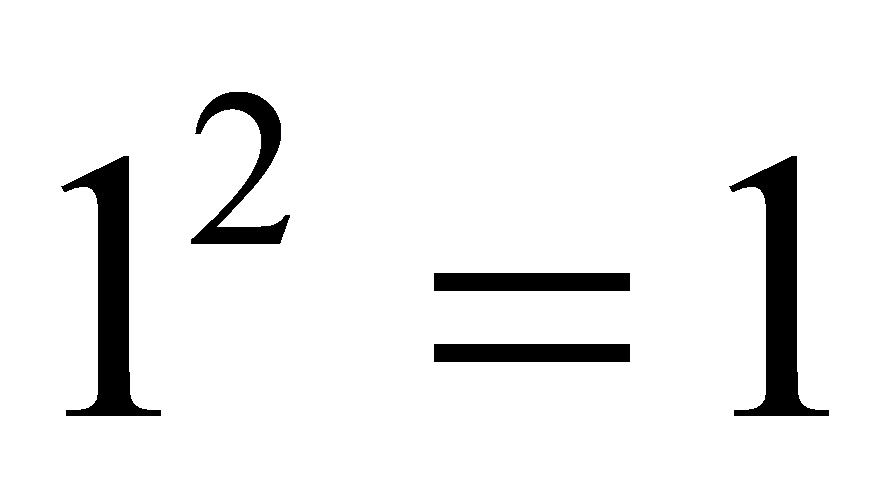 ,
, 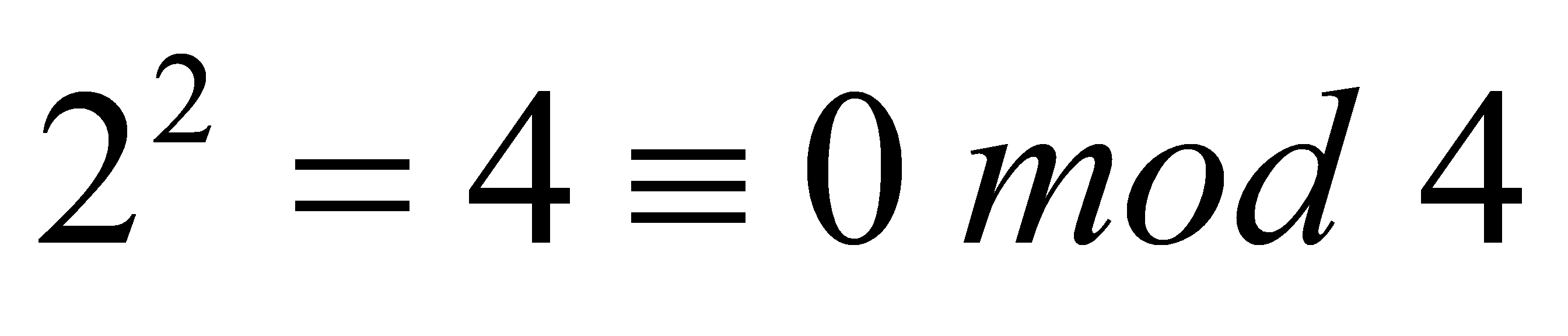 and
and , we found that squares are always congruent to
, we found that squares are always congruent to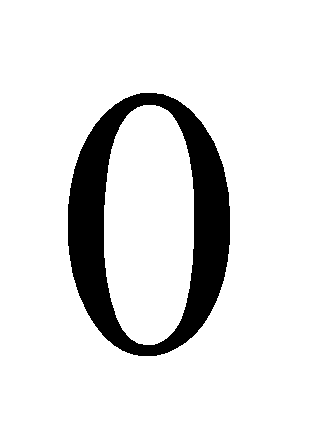 or
or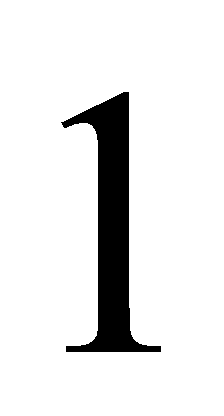 modulo
modulo . If
. If is a sum of two squares, then
is a sum of two squares, then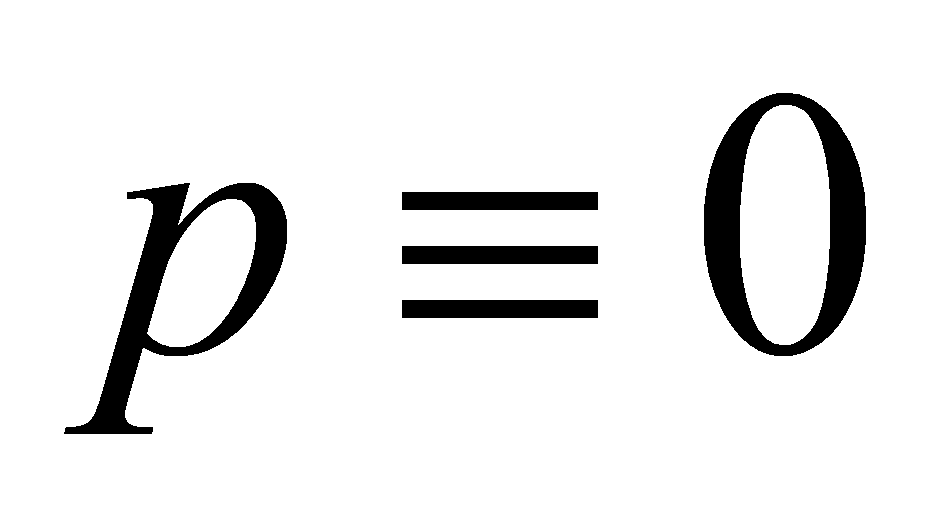 ,
, ,
,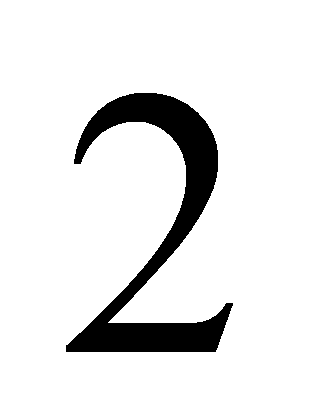 mod
mod . Then
. Then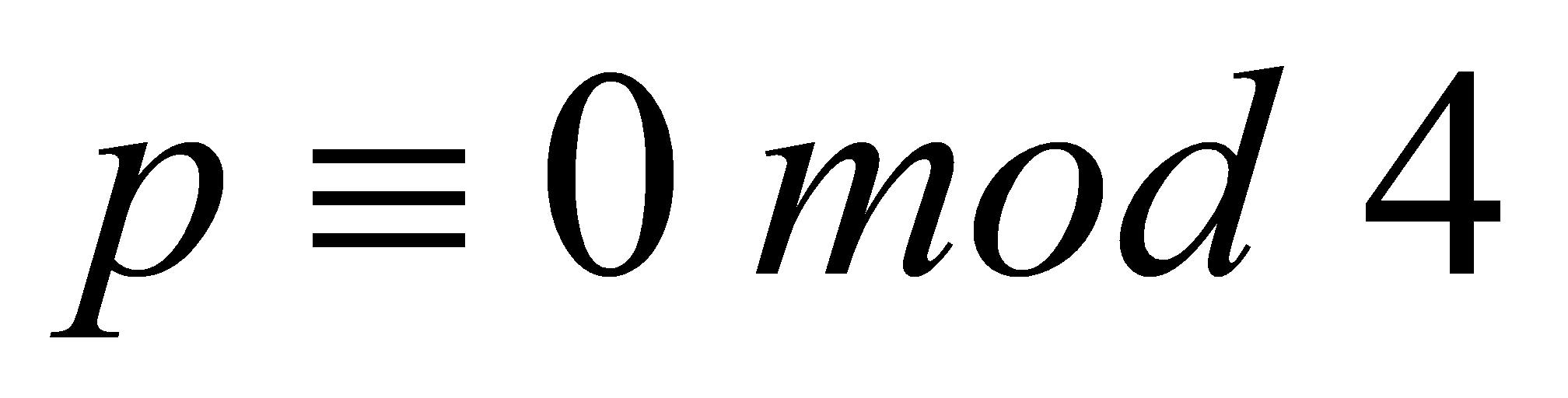 is impossible and the only prime congruent to
is impossible and the only prime congruent to modulo
modulo is
is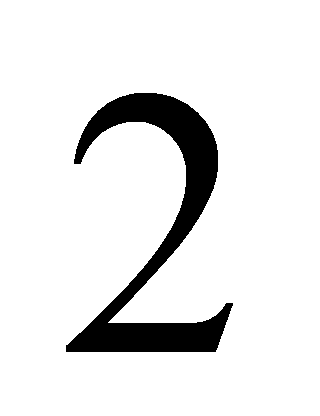 .
.
The less trivial reverse direction will be proved, showing that every prime can be written as
can be written as , with
, with . This will be done by factoring the ideal
. This will be done by factoring the ideal in the ring of integers
in the ring of integers of
of . The factorisation depends on the roots of
. The factorisation depends on the roots of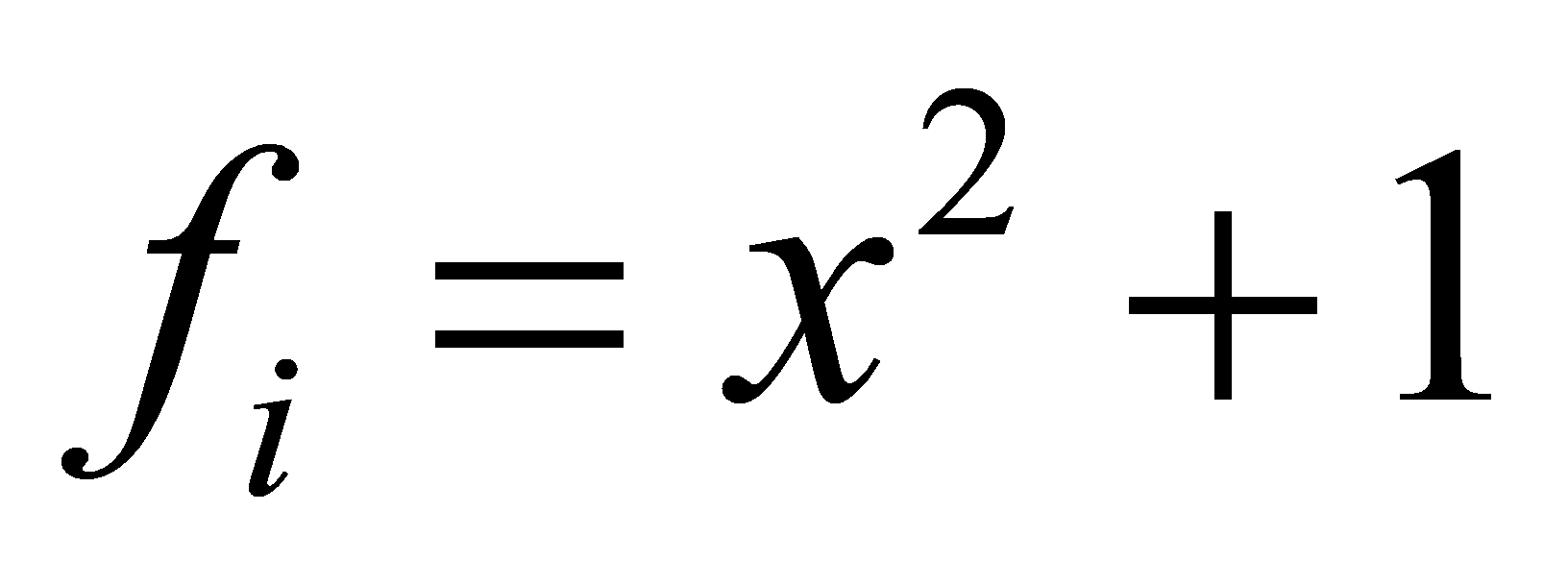 in
in .
.
Lemma 3.2. Let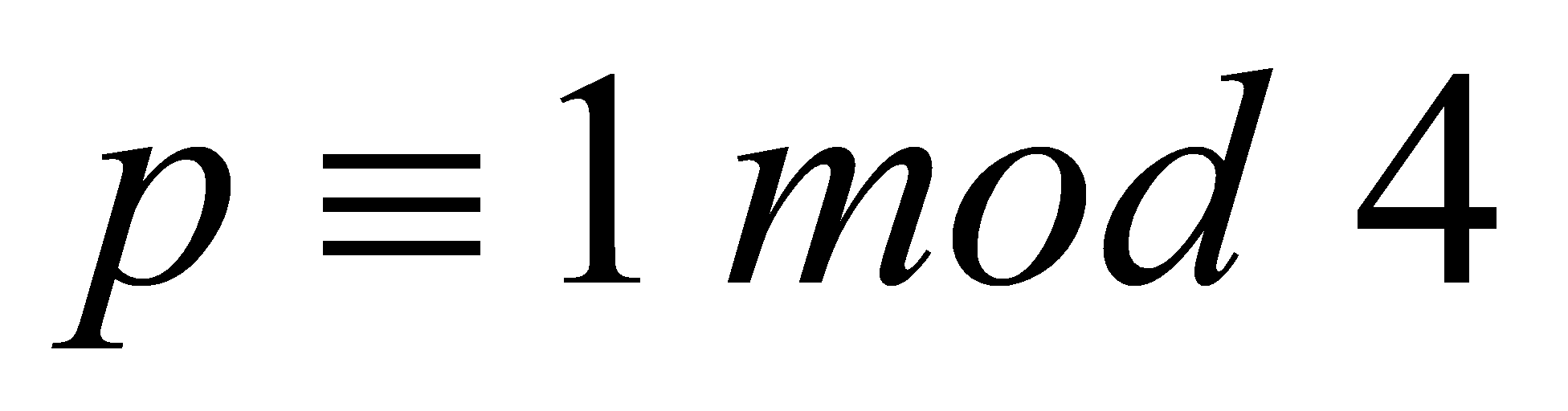 be a prime. Then
be a prime. Then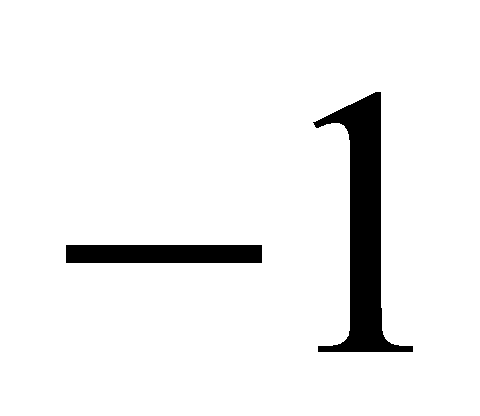 is a square modulo
is a square modulo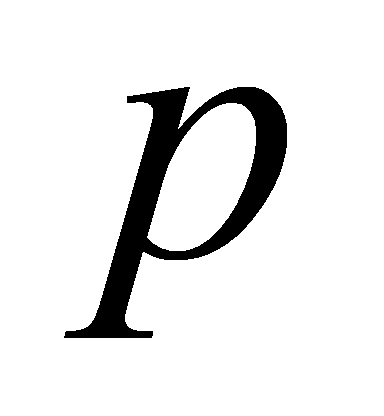 , i.e., there is
, i.e., there is with
with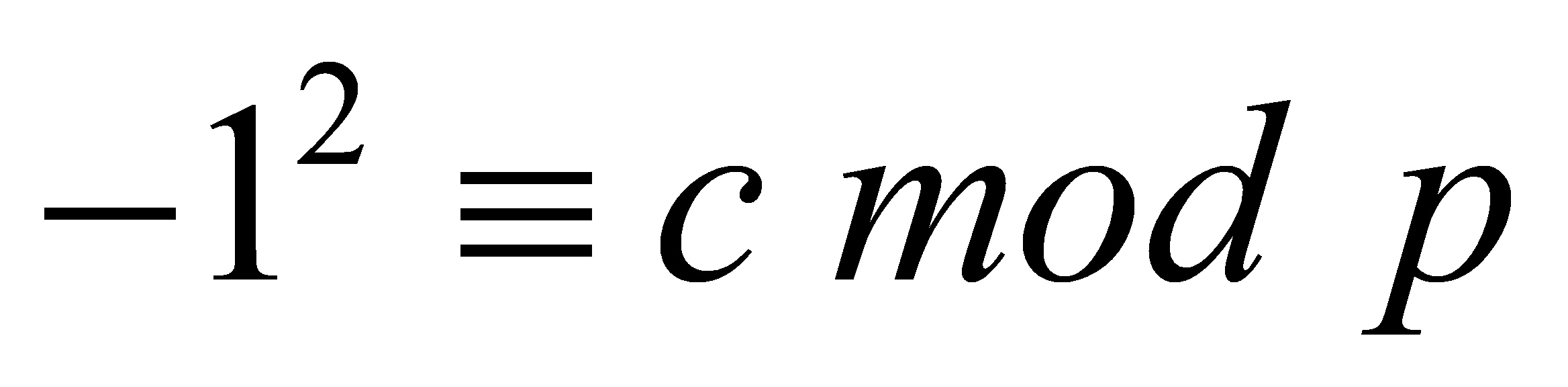 .
.
Proof. Let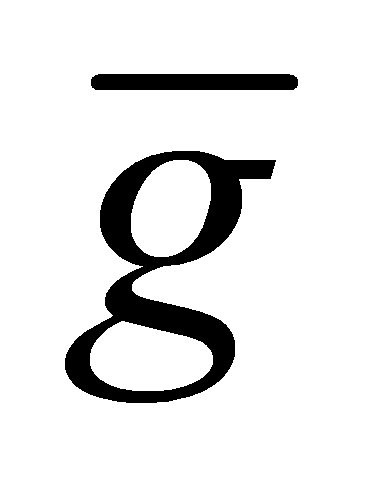 be a generator of
be a generator of , then
, then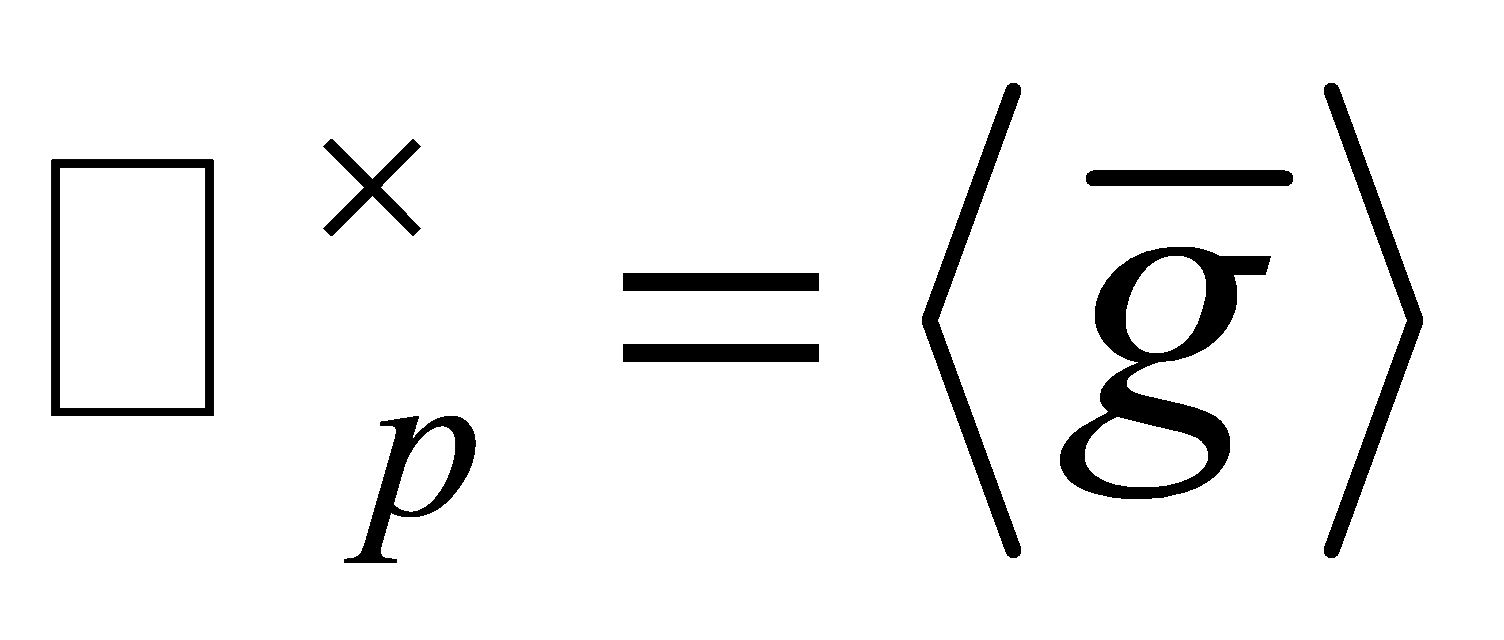 and write
and write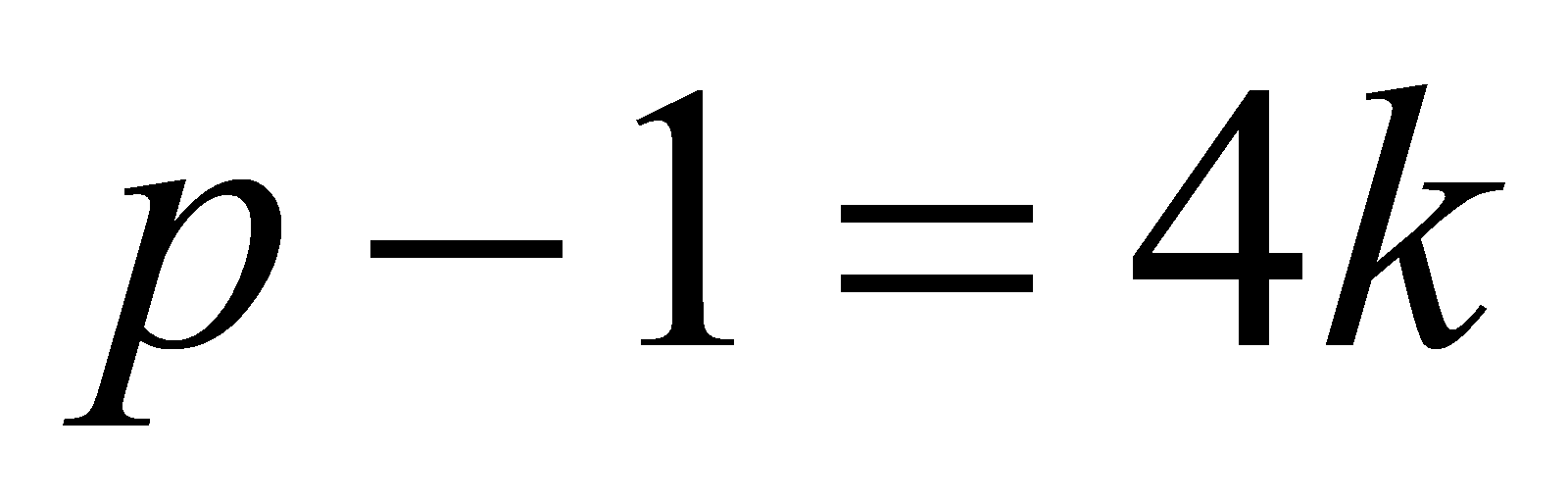 . By Fermat's Little Theorem, then
. By Fermat's Little Theorem, then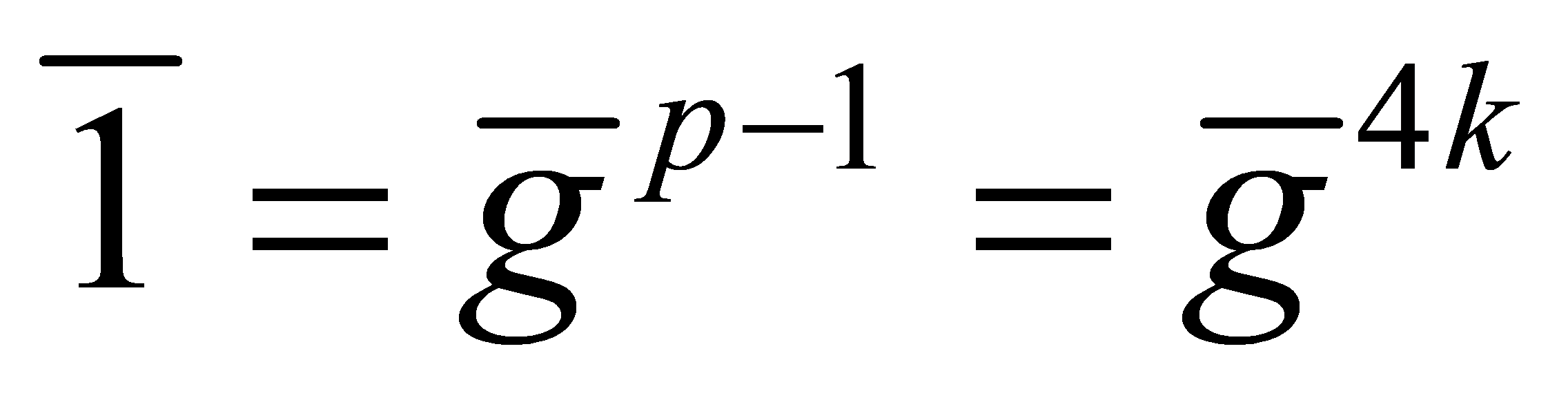 . The polynomial
. The polynomial has only two roots
has only two roots 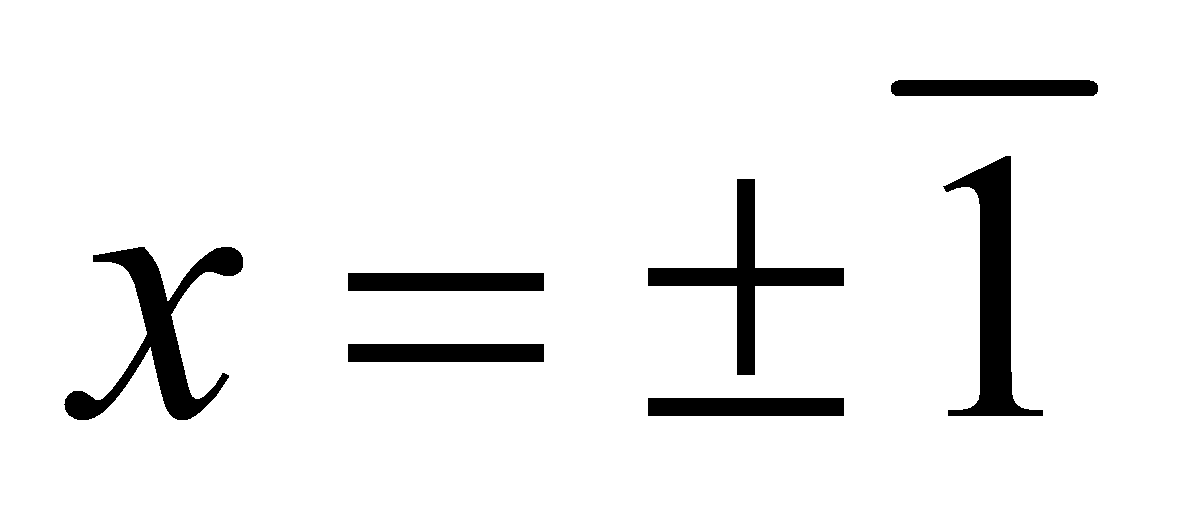 . Thus
. Thus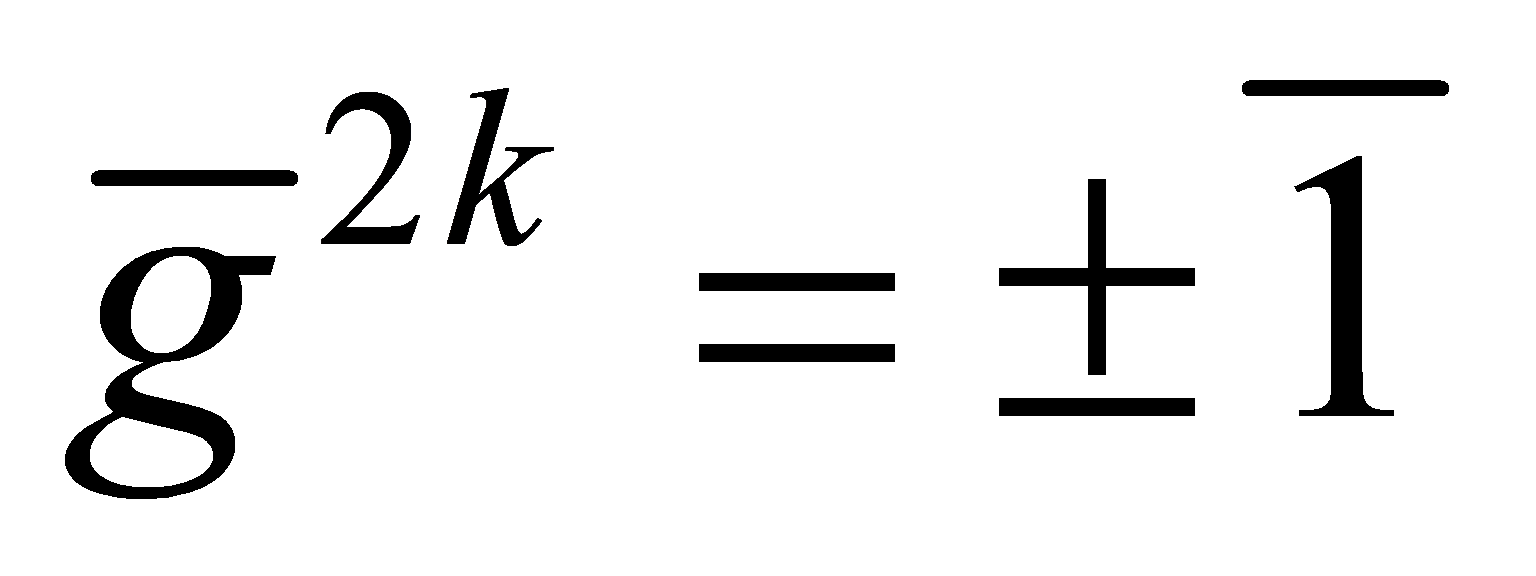 . If
. If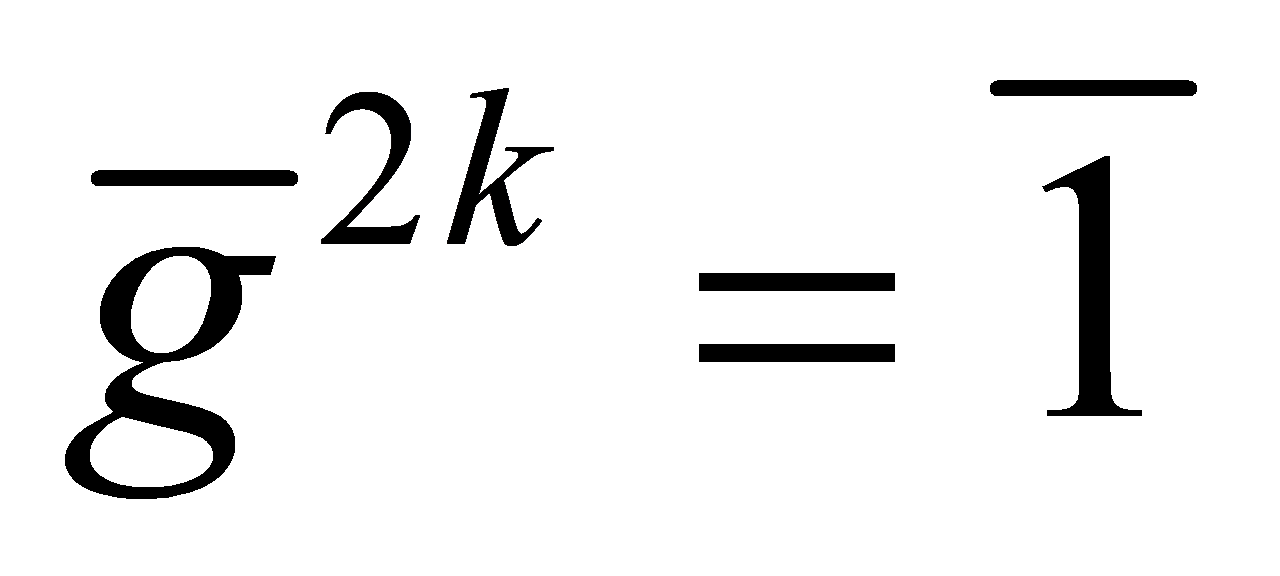 , so
, so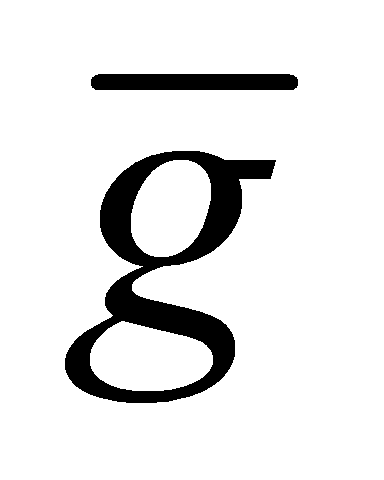 can not generate all of
can not generate all of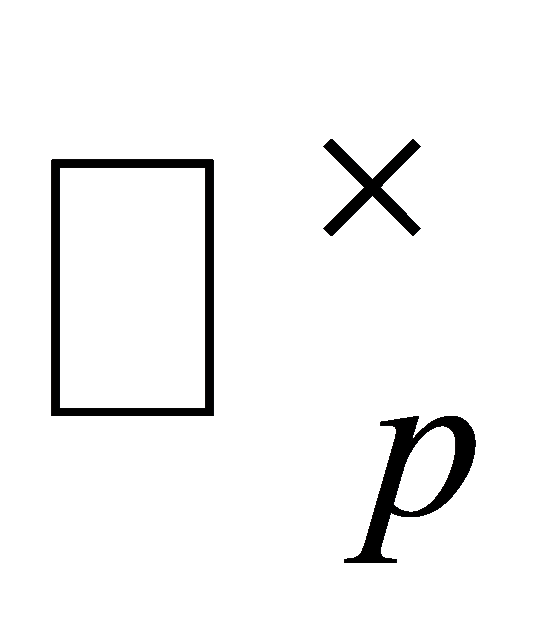 , as then
, as then  , so the powers
, so the powers , for
, for capture only
capture only elements of
elements of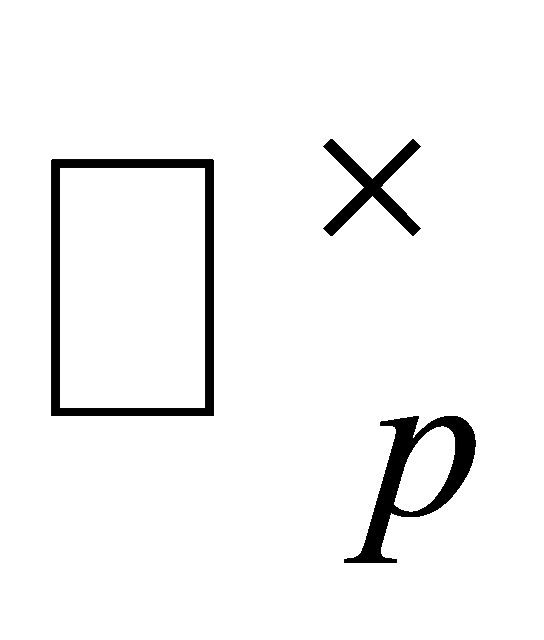 . Hence,
. Hence,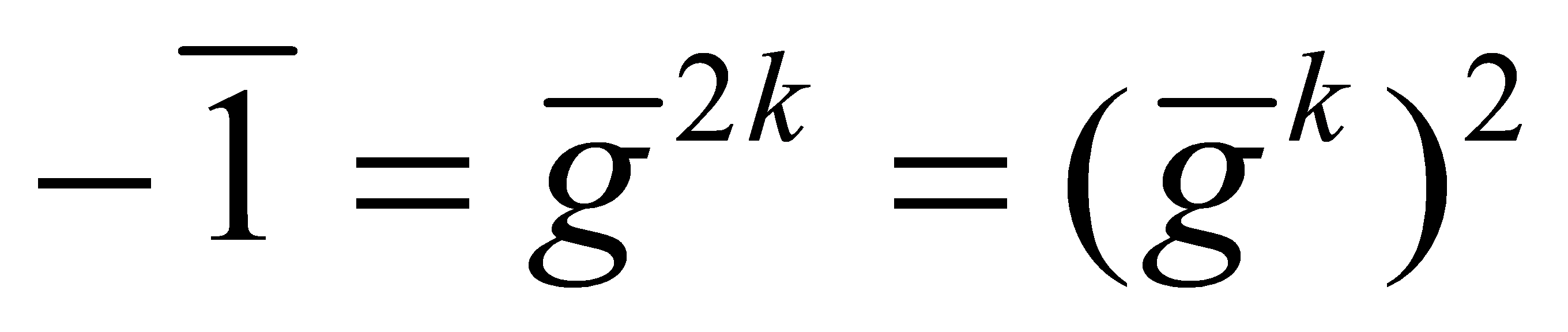 and thus,
and thus,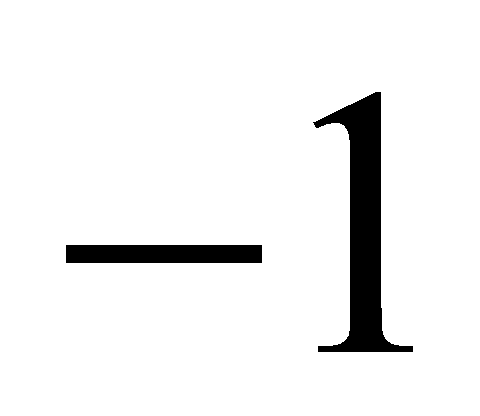 is a square modulo
is a square modulo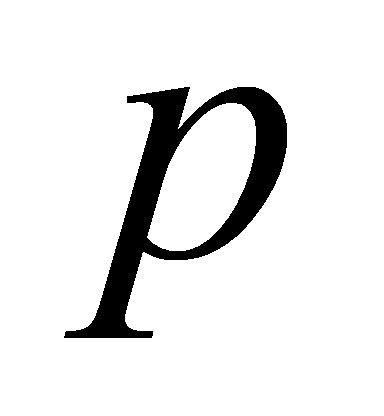 .
.
Theorem 3.3. Let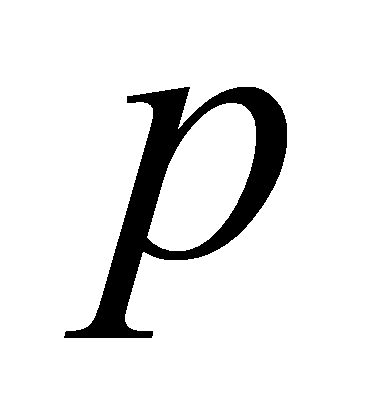 be an odd prime. Then
be an odd prime. Then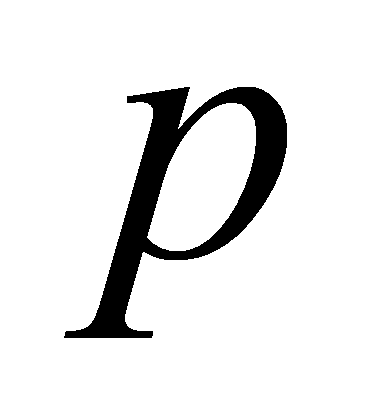 is a sum of two squares if and only if
is a sum of two squares if and only if 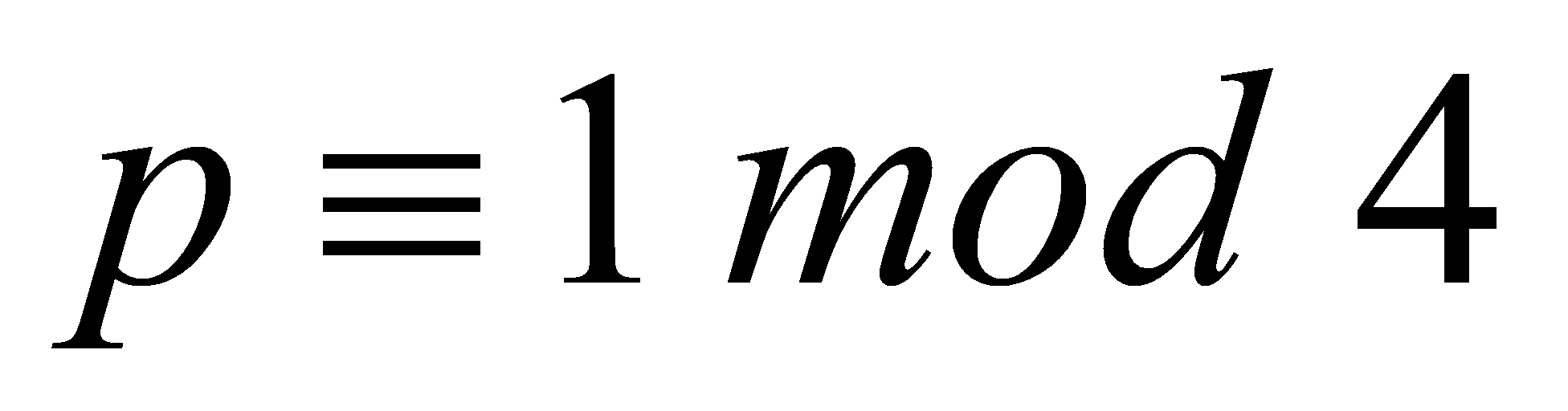 [8,9].
[8,9].
Proof. From Lemma 3.1, it is known that the "only if" part has been proved, so let us prove the "if" part. Let , then
, then . Consider the factorisation of the ideal
. Consider the factorisation of the ideal and note that
and note that . By Lemma 3.2, there is
. By Lemma 3.2, there is , such that
, such that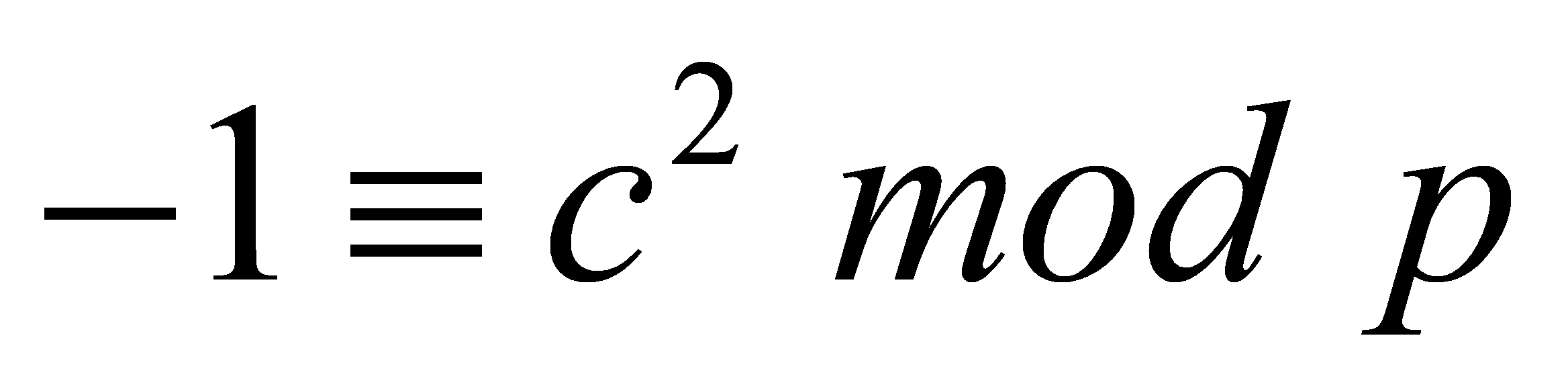 . Thus Equation (4) is obtained:
. Thus Equation (4) is obtained:
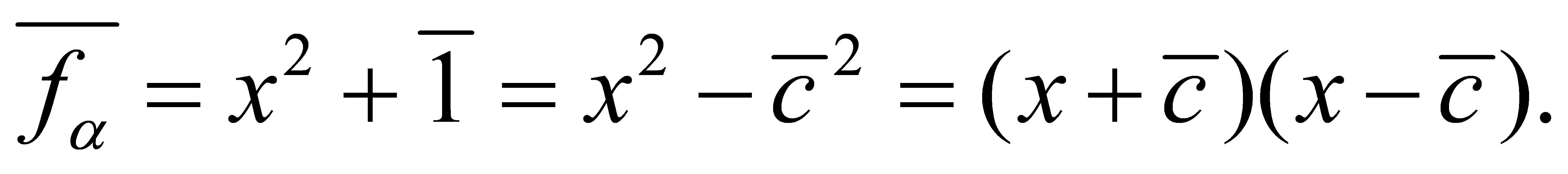 (4)
(4)
If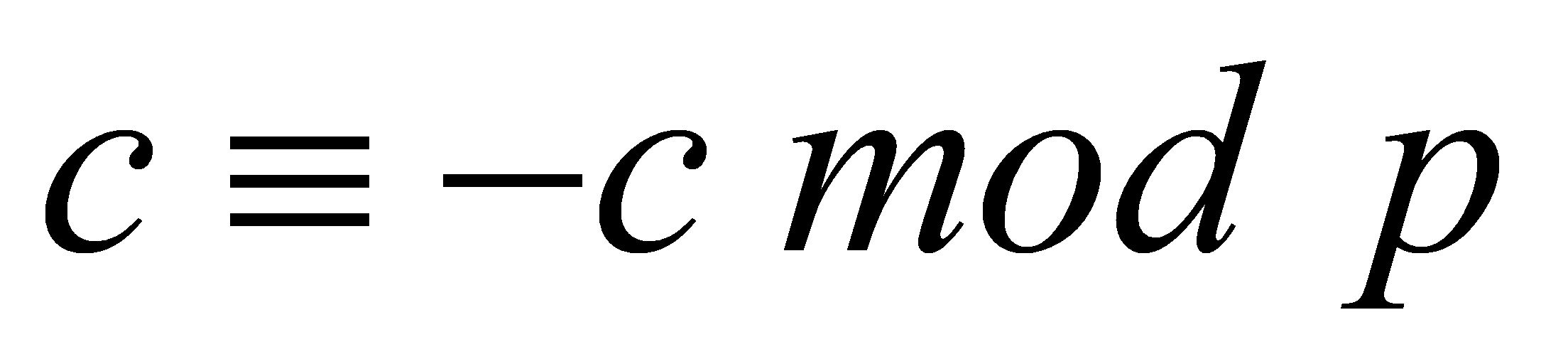 , then
, then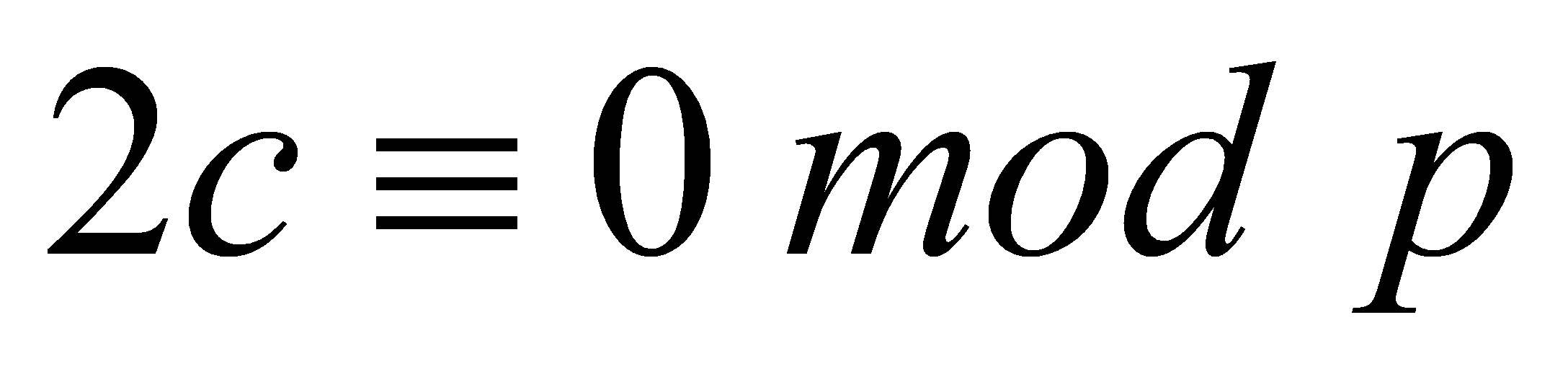 . Since
. Since , so there is only one possible value:
, so there is only one possible value:  , but that is impossible because
, but that is impossible because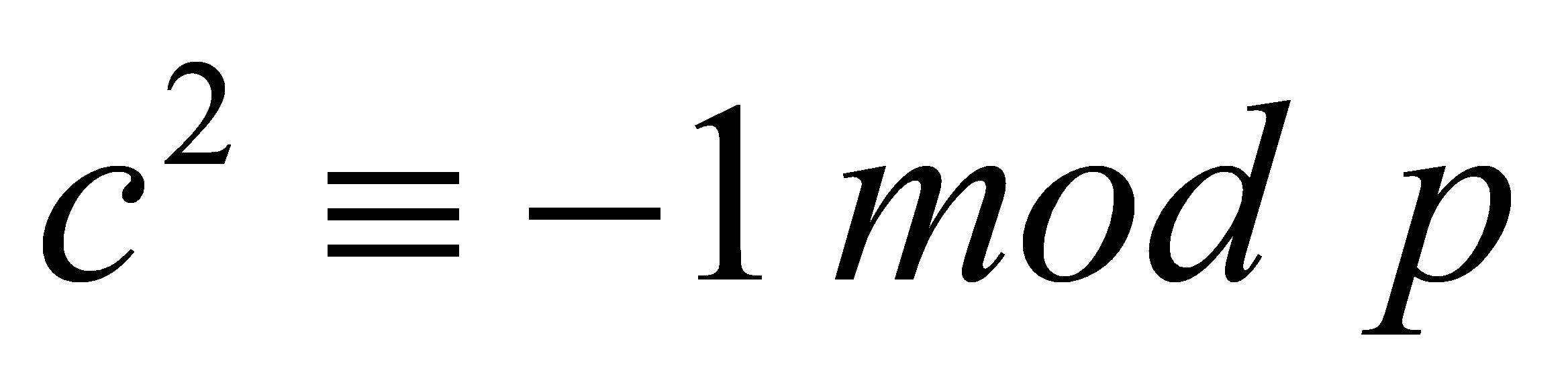 , thus
, thus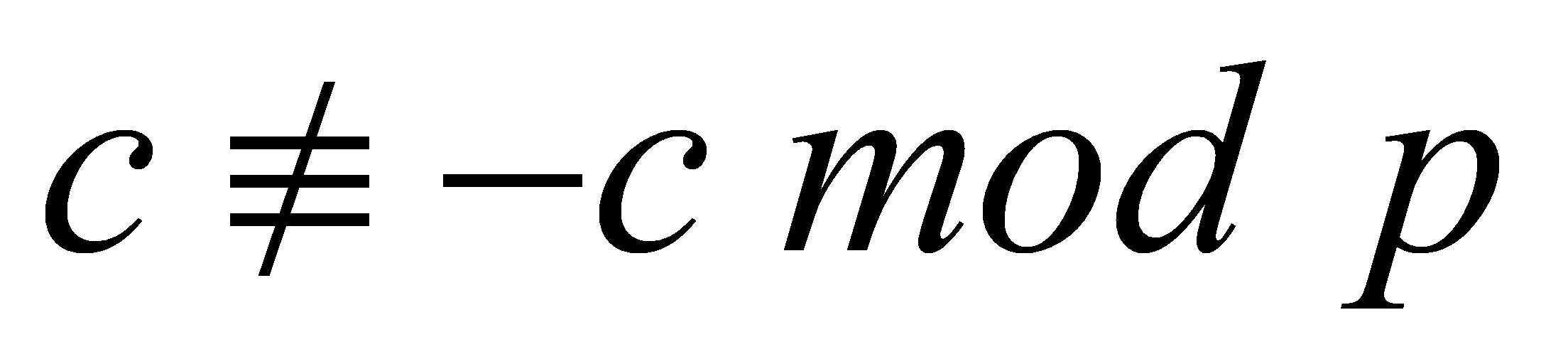 , so these are two distinct roots. Hence,
, so these are two distinct roots. Hence,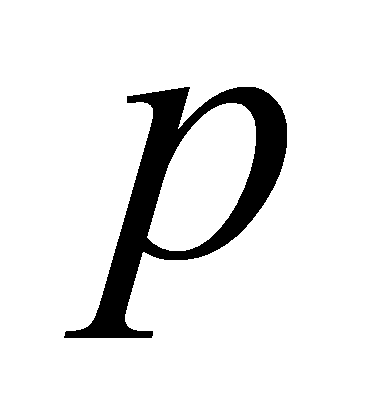 is split in
is split in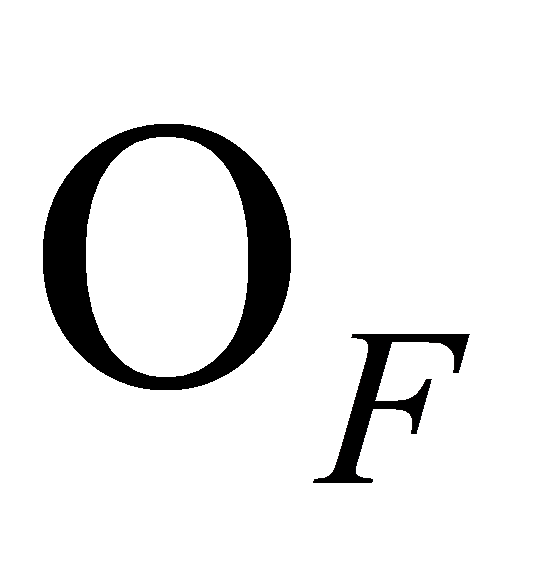 and
and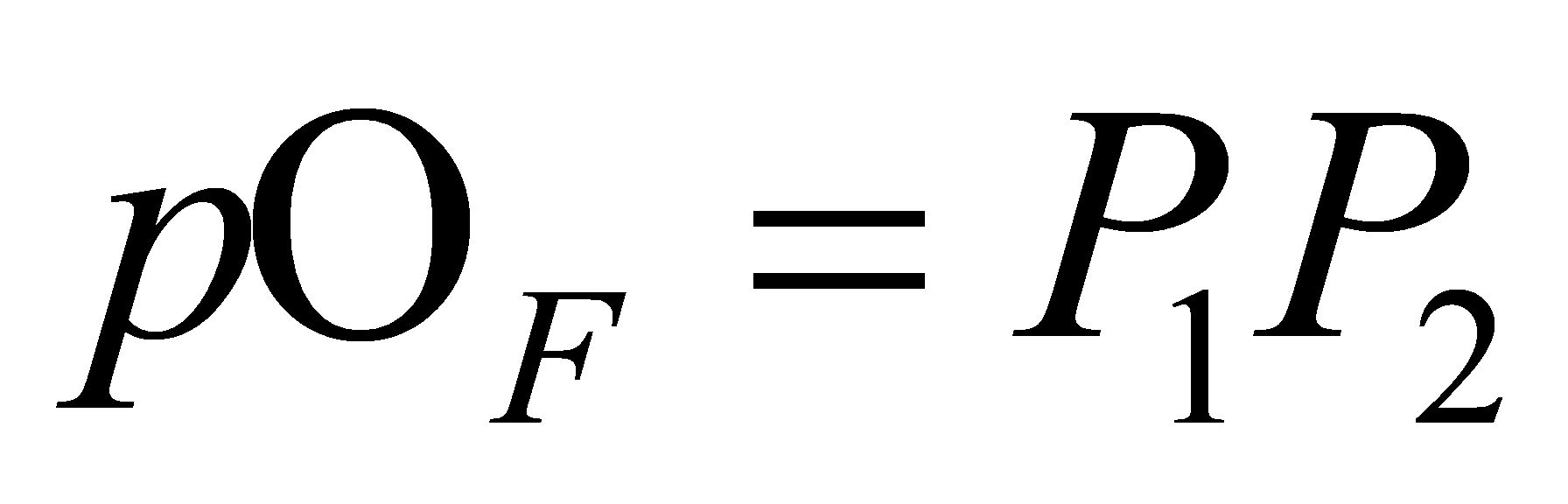 , for two distinct prime ideals
, for two distinct prime ideals with
with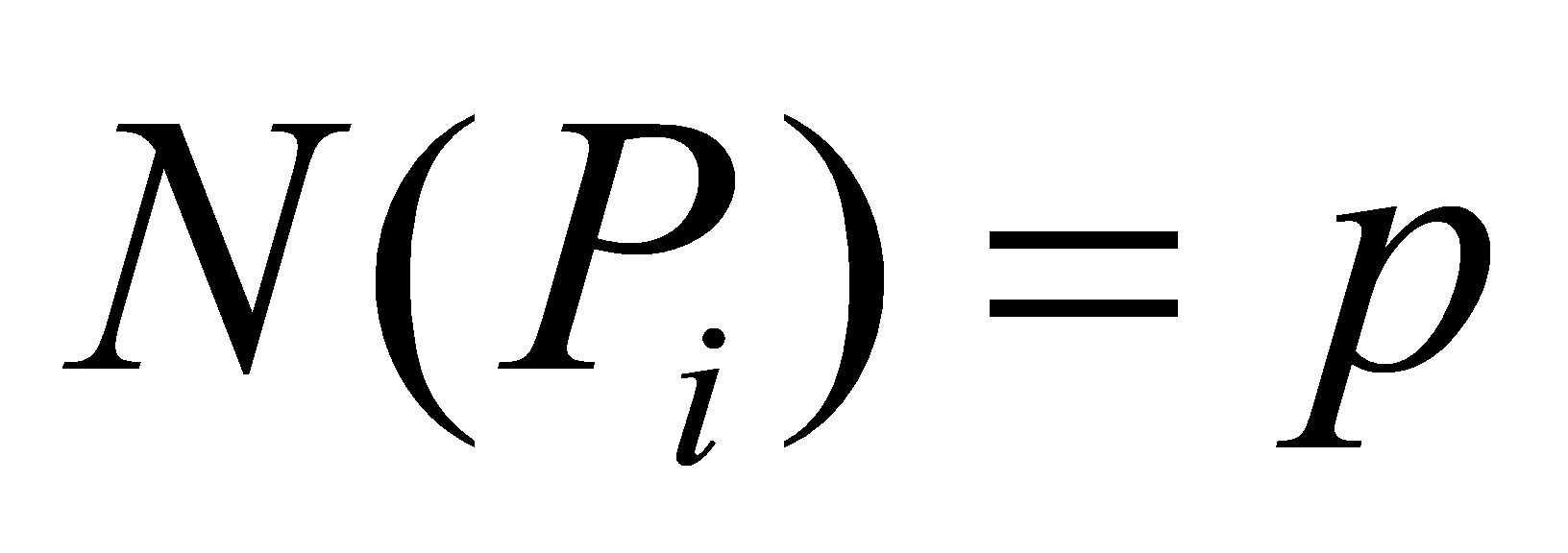 . Since every ideal of
. Since every ideal of is principle. Hence,
is principle. Hence,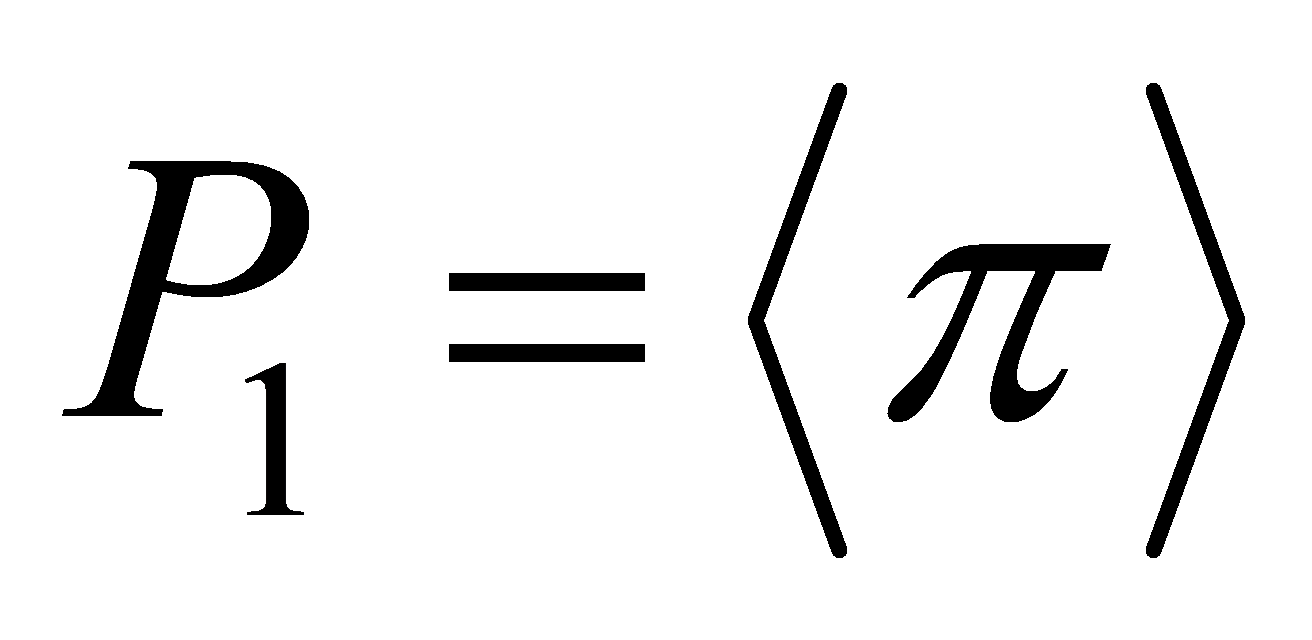 , for some
, for some  . Since
. Since and
and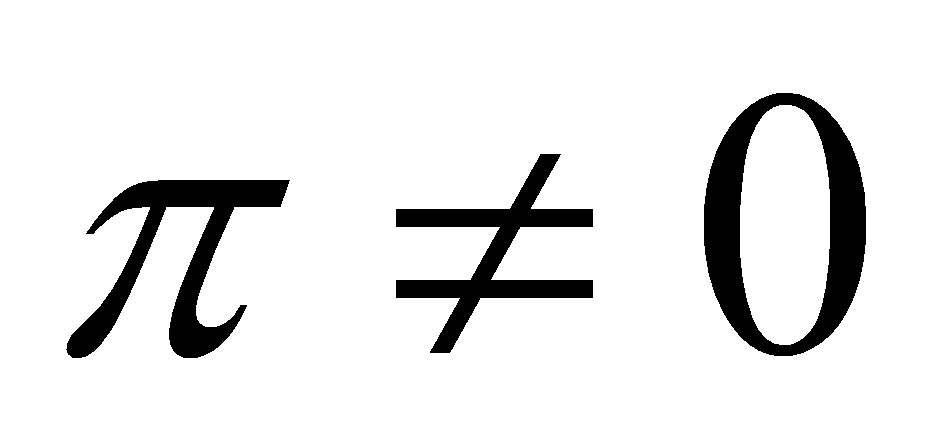 , then Equation (5) is obtained:
, then Equation (5) is obtained:
 (5)
(5)
4. Conclusion
This paper describes the process of decomposition of prime ideals and the corresponding applications: i.e., it discusses what kind of prime numbers can be written in the form of a sum of two integer squares and we got the result that for odd prime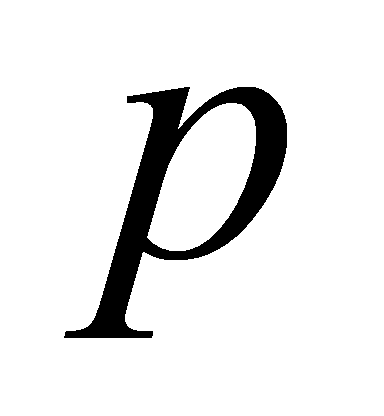 , it is a sum of two squares if and only if
, it is a sum of two squares if and only if 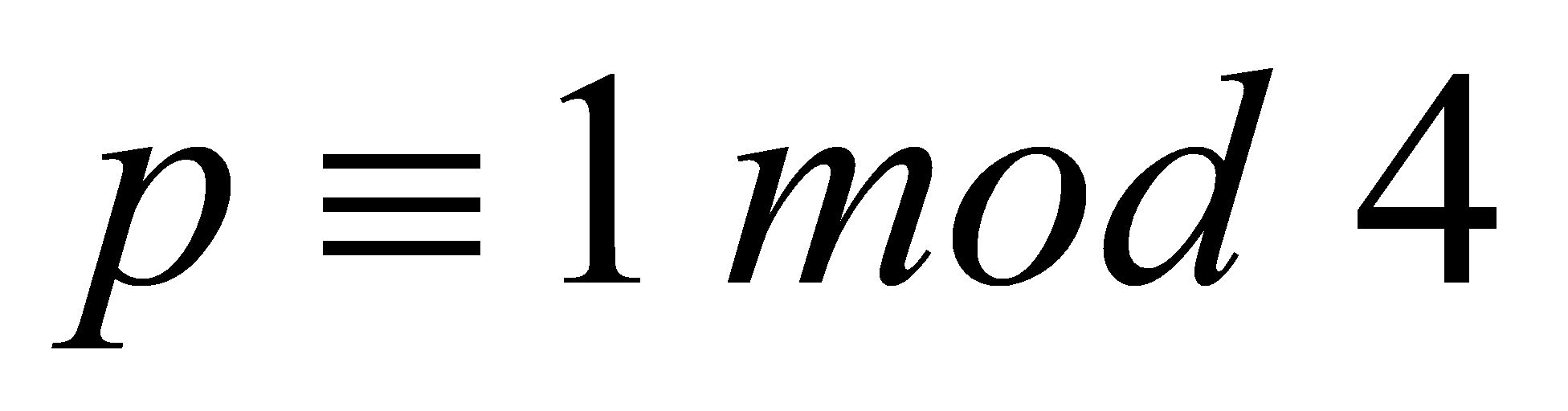 ,this part is a very classical part of algebraic number theory, on the basis of which if Minkowski bound and class groups, etc. are introduced, the property of the unique factorization domain (UFD) can be used to solve some problems about the Diophantine equations [10]. For instance, it can be shown that there are no
,this part is a very classical part of algebraic number theory, on the basis of which if Minkowski bound and class groups, etc. are introduced, the property of the unique factorization domain (UFD) can be used to solve some problems about the Diophantine equations [10]. For instance, it can be shown that there are no 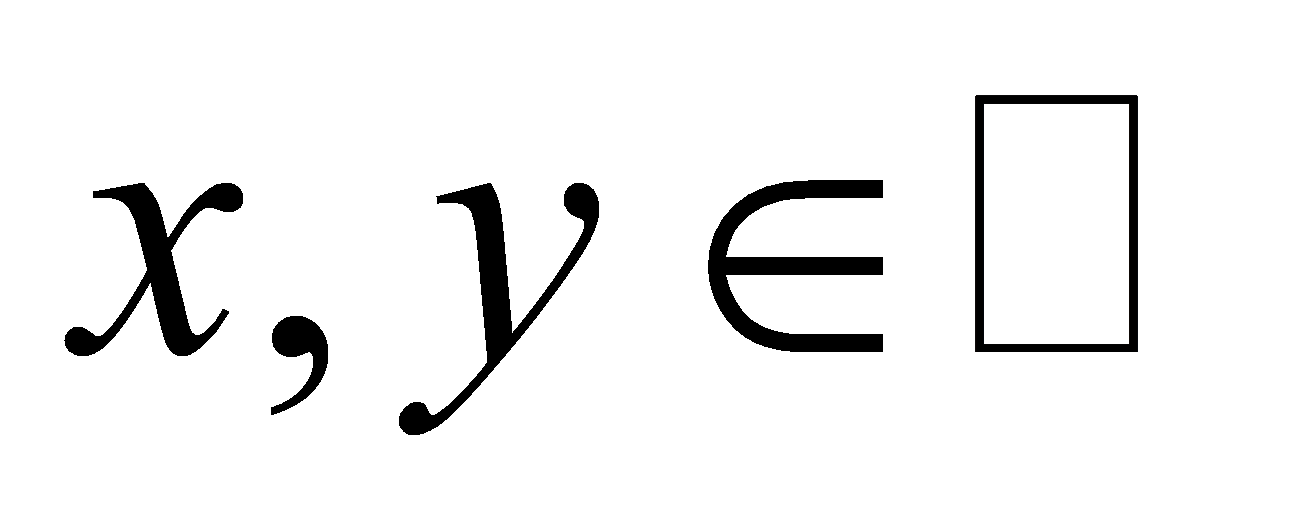 with
with 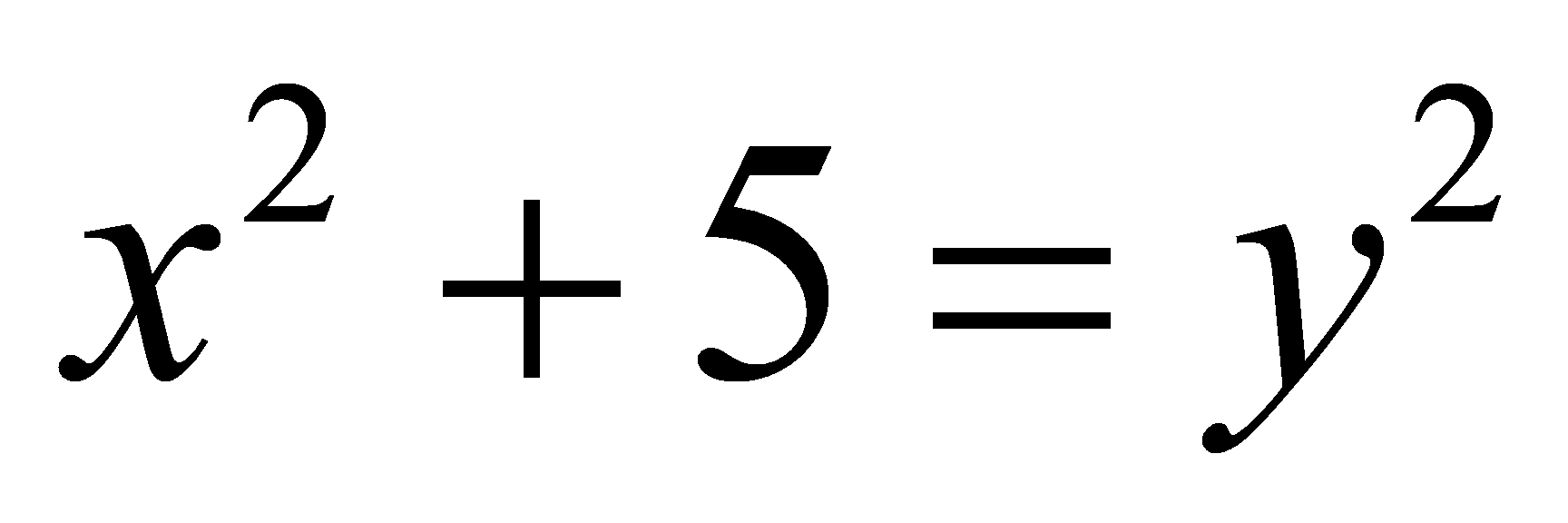 , which in the long run will be useful for the proof of Fermat's Last Theorem.
, which in the long run will be useful for the proof of Fermat's Last Theorem.
In the proof of the theorem, we use the fact that every ideal in is principle, we did not present the proof of this result in the article due to space constraints. Also, Theorem 2.9 can be applied to many number fields, but not all of them, that is because the assumption
is principle, we did not present the proof of this result in the article due to space constraints. Also, Theorem 2.9 can be applied to many number fields, but not all of them, that is because the assumption  , for some algebraic integer
, for some algebraic integer . But for many number fields, such an
. But for many number fields, such an does not exist, we just found such
does not exist, we just found such for quadratic and cyclotomic fields. Therefore, the results given in this article actually have certain limitations. On the basis of this problem, we can gradually try to use the idea of decomposition to consider proof of the special case of the Fermat’s last theorem for regular primes.
for quadratic and cyclotomic fields. Therefore, the results given in this article actually have certain limitations. On the basis of this problem, we can gradually try to use the idea of decomposition to consider proof of the special case of the Fermat’s last theorem for regular primes.
References
[1]. Bhaskar, J. (2008). Sum of two squares. https://www.math.uchicago.edu/~may/VIGRE/ VIGRE2008/REUPapers/Bhaskar.pdf.
[2]. Homeworkhelp. Com and Inc. Factoring and Primes (High School Math).
[3]. Stewart, I. and Tall, D. (2001). Algebraic Number Theory and Fermat's Last Theorem: Third Edition. A K Peters/CRC Press. ISBN-10: 1568811195. ISBN-13: 978-1568811192.
[4]. Edwards, H. M. (1977). Fermat's last theorem: A genetic introduction to algebraic number theory. In: Graduate Texts in Mathematics. Springer New York, NY.
[5]. Stein, M. R. and Dennis, R. K. (1989). Algebraic K-Theory and Algebraic Number Theory: Comtemporar Math., 83. American Mathematical Society, Providence.
[6]. Rosen, K. H. (2000). Elementary number theory and its applications. Addison Wesley. ISBN-10: 0201870738. ISBN-13: 978-0201870732.
[7]. Zagier, D. (1990). A One-Sentence Proof That Every Prime p Is a Sum of Two Squares. In: American Mathematical Monthly 97(2), 144.
[8]. Honsberger, R. (1970). Writing a Number as a Sum of Two Squares. In Ingenuity In Mathematics (Anneli Lax New Mathematical Library, pp. 61-66). Mathematical Association of America. doi:10.5948/UPO9780883859384.012.
[9]. Vladimirovich, D. V. and Genadievna, S. A. (2017). A generalization of fermat’s theorem on sum of two squares. Austrian Journal of Technical and Natural Sciences.
[10]. Ore, O. (1988). Number theory and its history (Dover Books on Mathematics). Dover Publications. ISBN-10: 0486656209. ISBN-13: 978-0486656205.
Cite this article
Jiang,Z. (2023). Factoring primes and sums of two squares. Theoretical and Natural Science,13,18-22.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Computing Innovation and Applied Physics
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Bhaskar, J. (2008). Sum of two squares. https://www.math.uchicago.edu/~may/VIGRE/ VIGRE2008/REUPapers/Bhaskar.pdf.
[2]. Homeworkhelp. Com and Inc. Factoring and Primes (High School Math).
[3]. Stewart, I. and Tall, D. (2001). Algebraic Number Theory and Fermat's Last Theorem: Third Edition. A K Peters/CRC Press. ISBN-10: 1568811195. ISBN-13: 978-1568811192.
[4]. Edwards, H. M. (1977). Fermat's last theorem: A genetic introduction to algebraic number theory. In: Graduate Texts in Mathematics. Springer New York, NY.
[5]. Stein, M. R. and Dennis, R. K. (1989). Algebraic K-Theory and Algebraic Number Theory: Comtemporar Math., 83. American Mathematical Society, Providence.
[6]. Rosen, K. H. (2000). Elementary number theory and its applications. Addison Wesley. ISBN-10: 0201870738. ISBN-13: 978-0201870732.
[7]. Zagier, D. (1990). A One-Sentence Proof That Every Prime p Is a Sum of Two Squares. In: American Mathematical Monthly 97(2), 144.
[8]. Honsberger, R. (1970). Writing a Number as a Sum of Two Squares. In Ingenuity In Mathematics (Anneli Lax New Mathematical Library, pp. 61-66). Mathematical Association of America. doi:10.5948/UPO9780883859384.012.
[9]. Vladimirovich, D. V. and Genadievna, S. A. (2017). A generalization of fermat’s theorem on sum of two squares. Austrian Journal of Technical and Natural Sciences.
[10]. Ore, O. (1988). Number theory and its history (Dover Books on Mathematics). Dover Publications. ISBN-10: 0486656209. ISBN-13: 978-0486656205.









