1. Introduction

The study of p-adic numbers has been a cornerstone of the field of number theory, providing deep insights into the divisibility of rational numbers and a unique framework for understanding the complex interplay of prime numbers in mathematics [1, 2]. This article examines the definitions, characteristics, and theoretical underpinnings of p-adic numbers.

In the field of mathematics based on integers and rational numbers, p-adic numbers emerged as a significant extension, providing a novel perspective on number theory. Their significance lies not only in their intrinsic mathematical beauty but also in their practical use. P-adics have applications in many branches of mathematics, including algebraic number theory, Diophantine equations, and transcendental number theory, by revealing the structure of divisibility within rational numbers [3, 4, 5, 6].

This research seeks to elucidate the theoretical framework underpinning p-adic numbers, revealing their unique properties and their role in advancing our understanding of number theory. By delving into their definitions, properties, and theoretical implications, we aim to provide a comprehensive overview of p-adic numbers and their enduring relevance in contemporary mathematical research.

2. Motivation

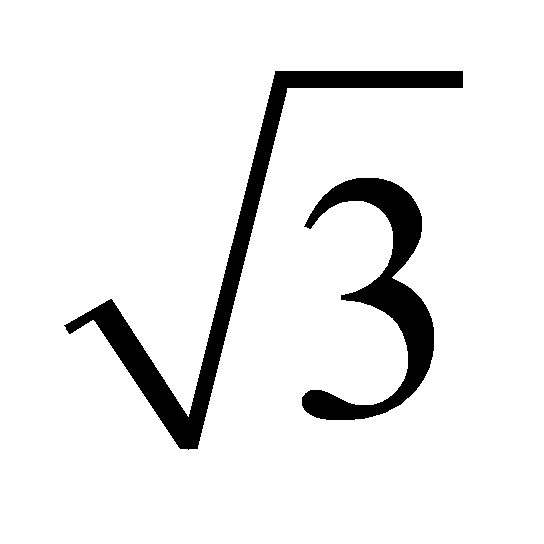is an irrational number which can be expressed by:

(1)

How can express this irrational number into a sequence \( xk \) of rational numbers? let’s consider a quadratic congruence:

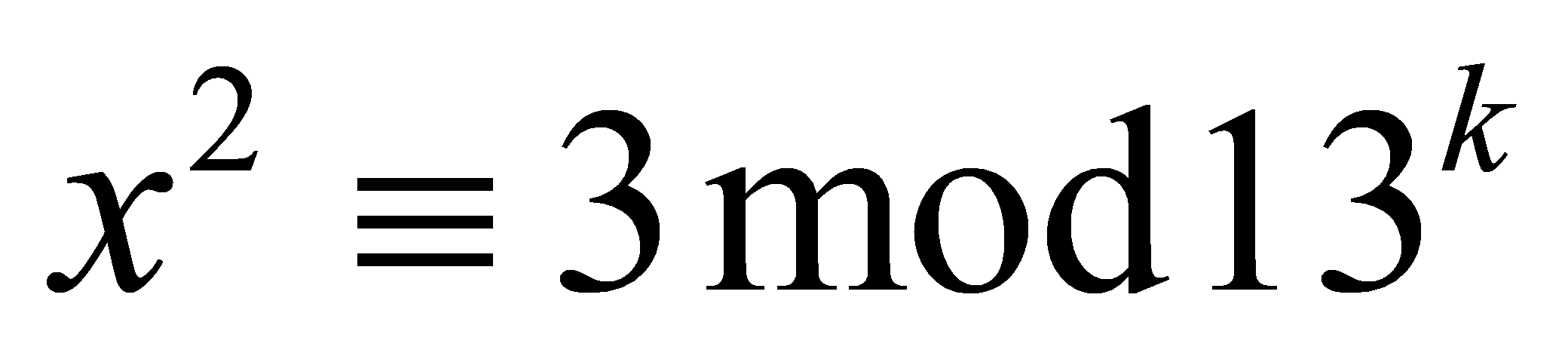,(2)

and \( k = 1,2,3... \) for \( k = 1 \) , the solutions are 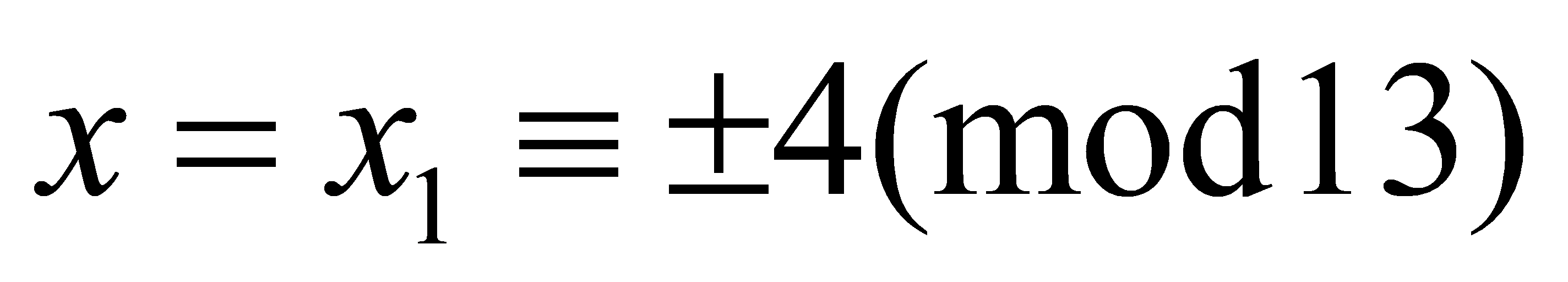for \( k = 2 \) , it can also find the solution that is 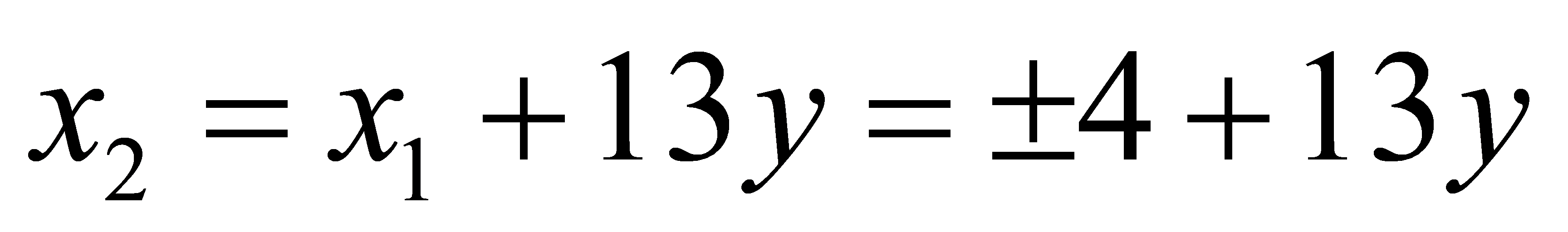. Let \( x1 = 4 \) , check the equation:

,(3)

the only solution of \( y \) is 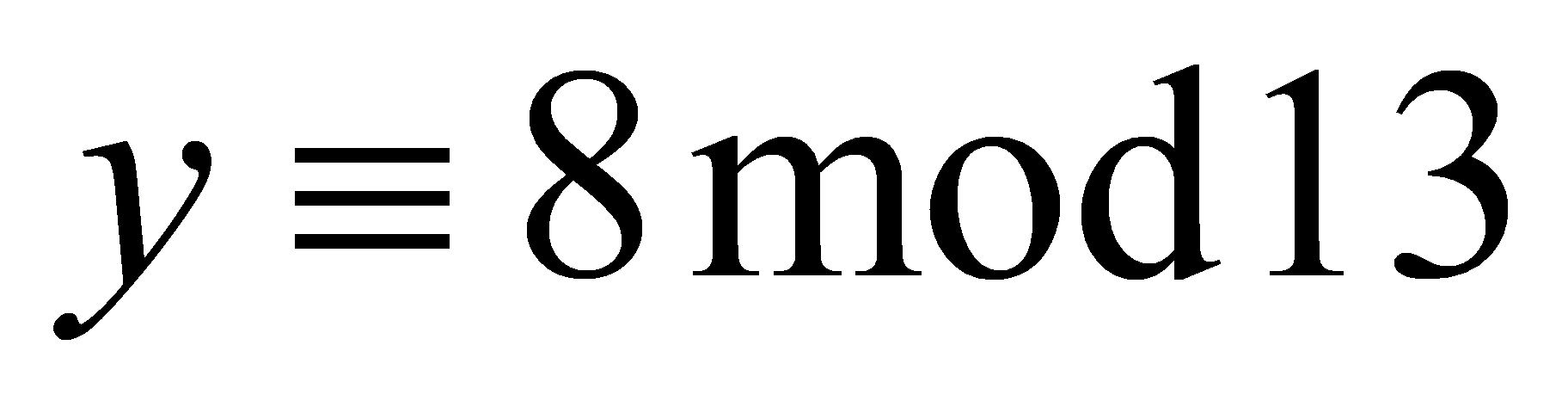, so .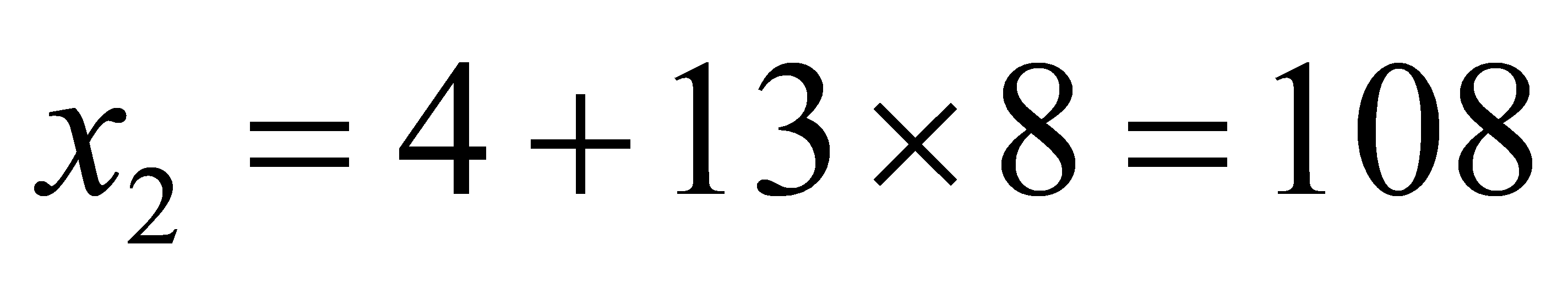

With a similar method, it can keep deducing \( x3, x4 \) an,d so on. Now there is some sort of “sequence” that \( xk \) satisfies that can be discovered, 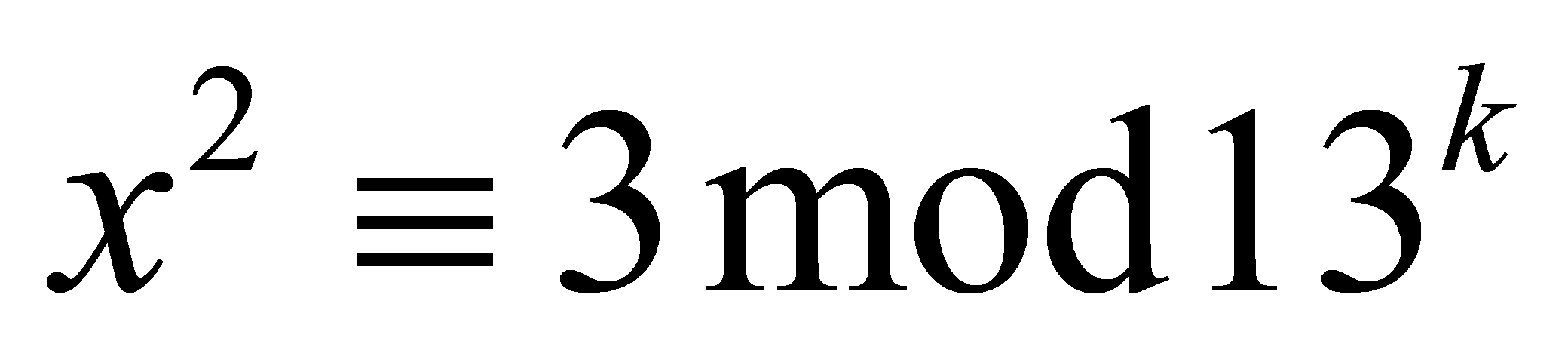but no particular \( x \) satisfies for all \( n \) .

Then the paper needs to define a kind of number called p-adic number, which can show the relationship of 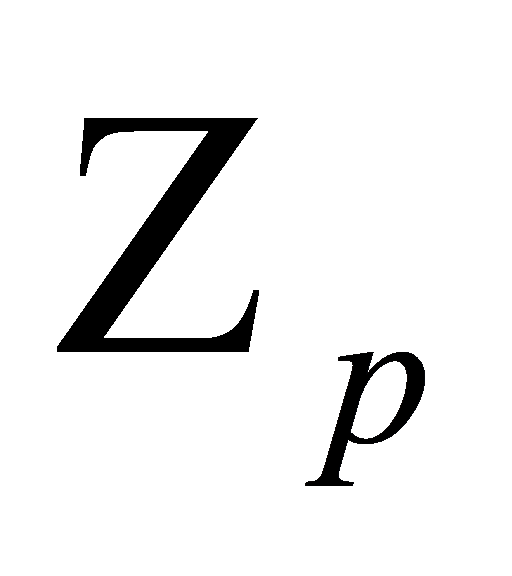elements in the group for each prime number [7].

3. Basic lemmas

Lemma 3.1. The following form is the only way to express any non-zero rational number:

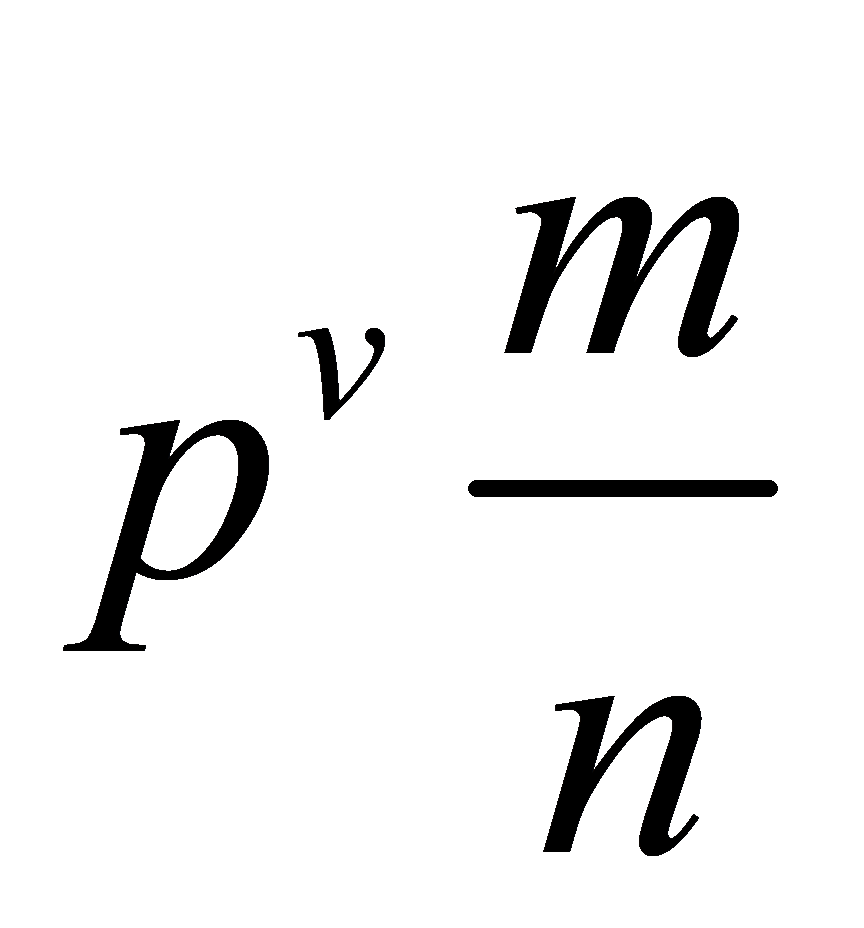,(4)

where \( n, m \) , and n are all integers, \( p \) is a prime number, and neither m nor n is divisible by \( p \) . P-adic valuation of the rational number is referred to as v.

It must employ the fundamental theorem of mathematics to prove this lemma. It asserts that, regardless of the arrangement of the prime components, every positive integer greater than 1 may be written in a particular form as a multiplication of prime integers. For example, \( 1000 = 2 ×2×2×5×5×5 = 23 ×53 \) . Obviously, the formula of nonzero rational number can be directly deduced from the fundamental theorem of arithmetic.

Lemma 3.2. The only way to express each non-zero rational number \( r \) with \( a \) valuation \( v \) is as 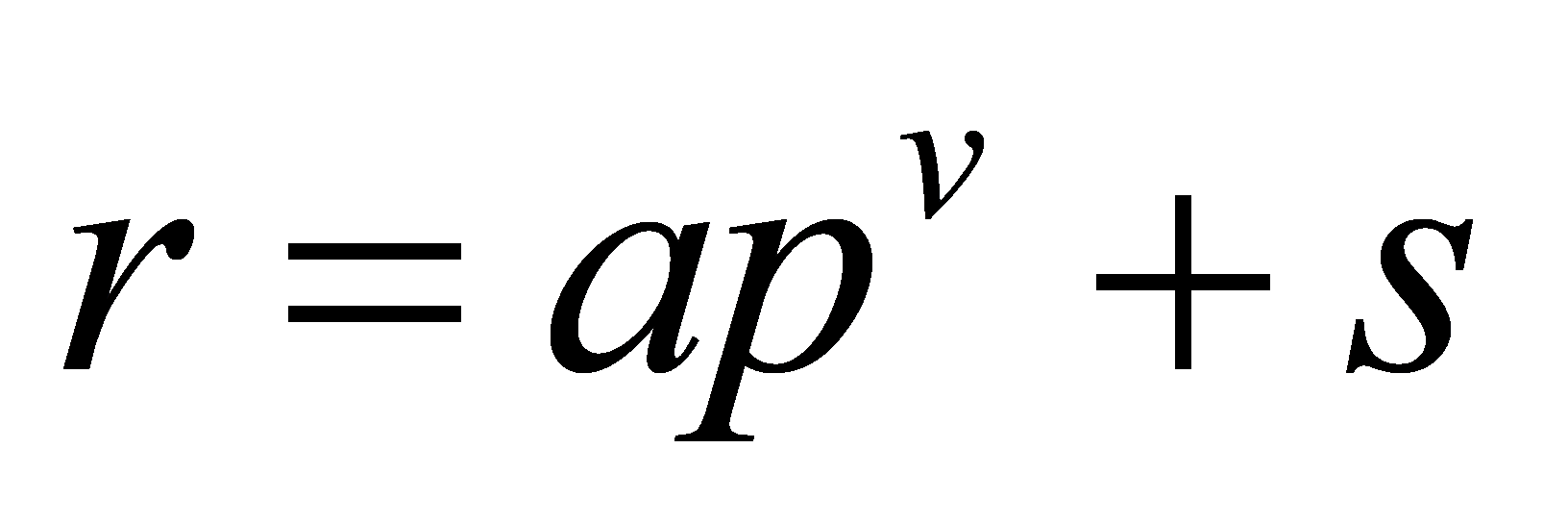follows: where an is an integer such that and s is a rational number with value greater than \( v \) :

\( 0 \lt a \lt p \) ,(5)

Lemma 3.2 can be deduced from the first lemma. By lemma 2.1, 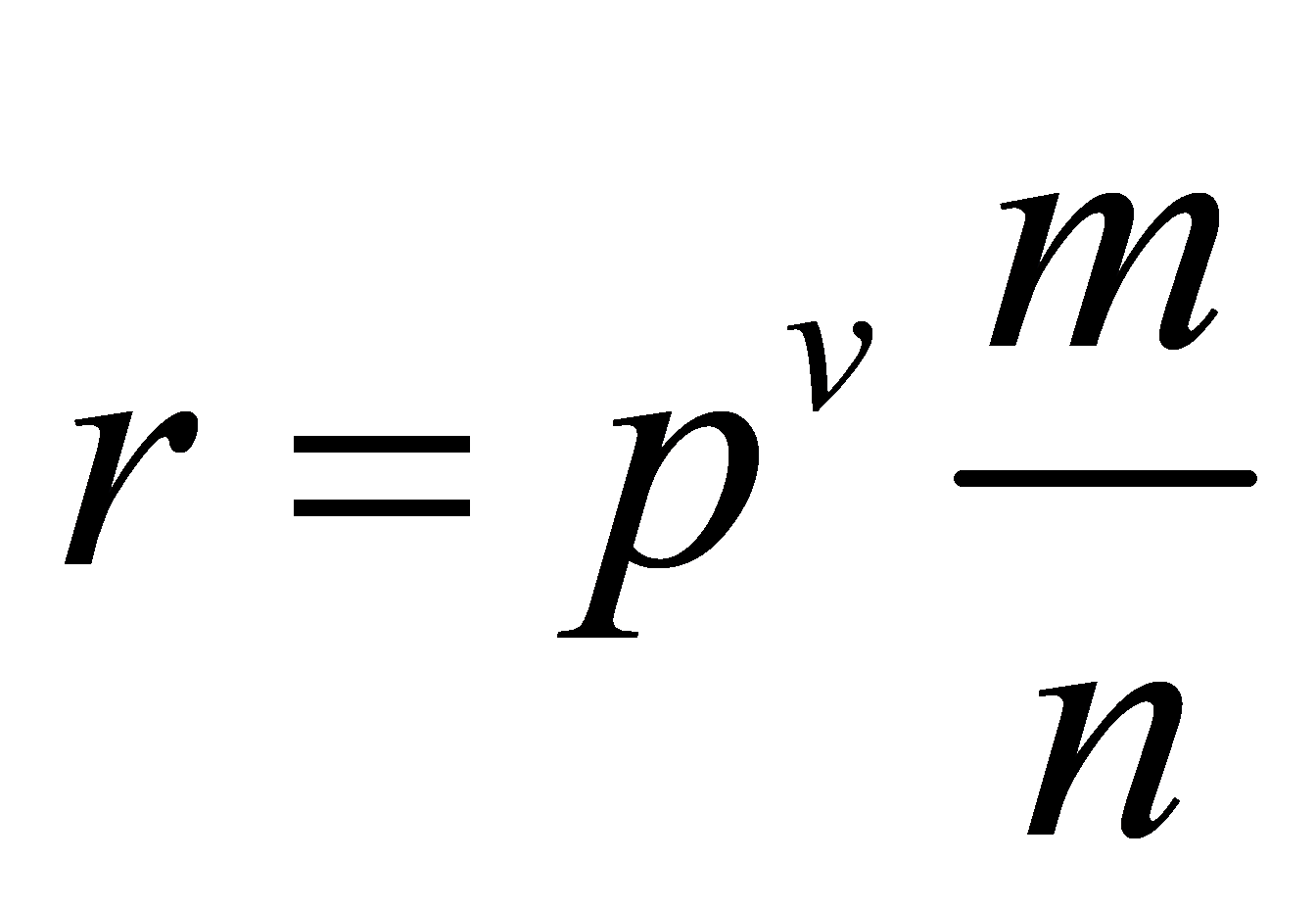, the modular inverse of \( n \) can be expressed as \( q \) such that \( nq = 1 + ph \) , where \( q \) and \( h \) are both integer. Then substitute \( 1/n = q-p(hm/n) \) . into the formula of \( r \) and get:

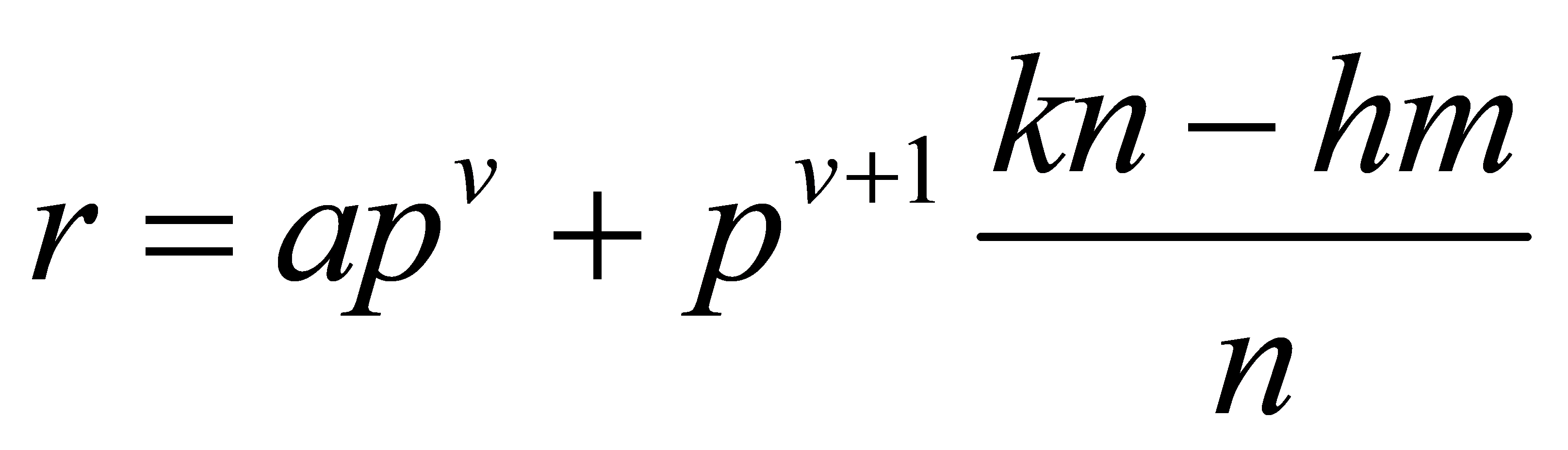(6)

which is lemma 2.2 states [8].

4. p-adic integer Z_p

4.1. p-adic numberd

Definition 4.1 (p-adic series). A power series expression of a mathematical series is known as a p-adic series:

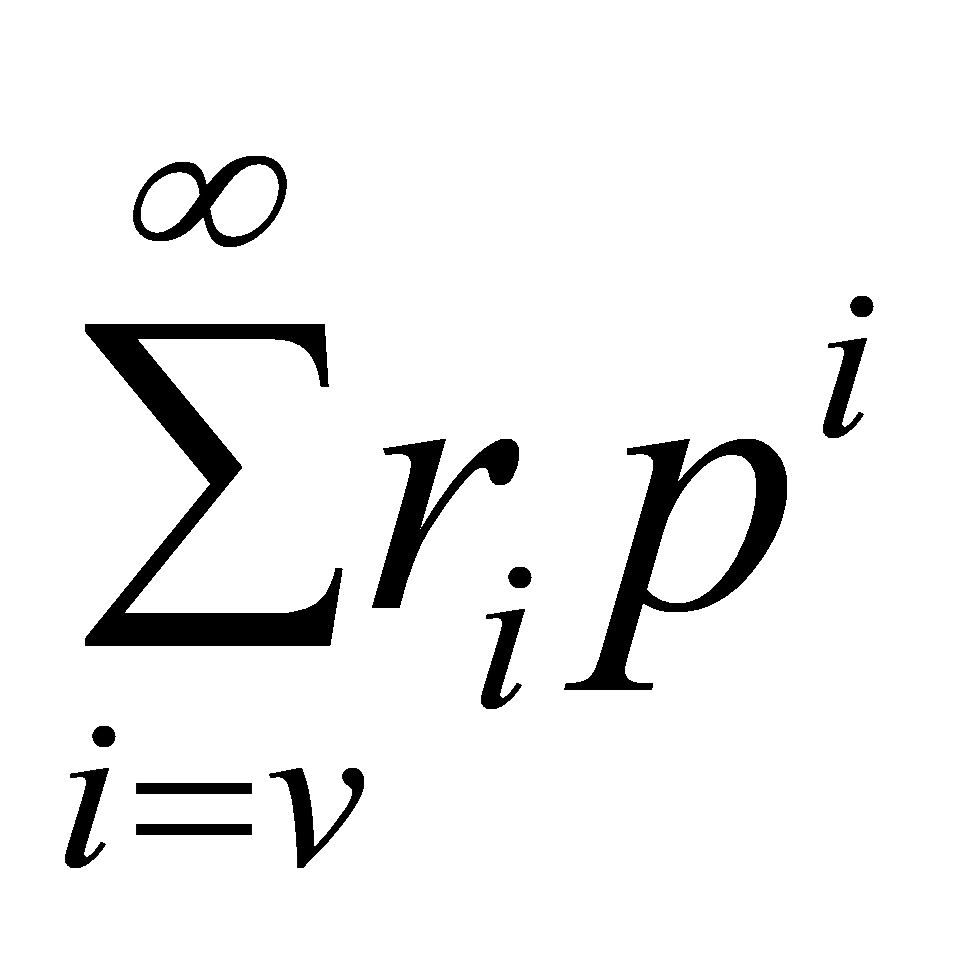,(7)

where \( v \) is an integer, and the coefficients 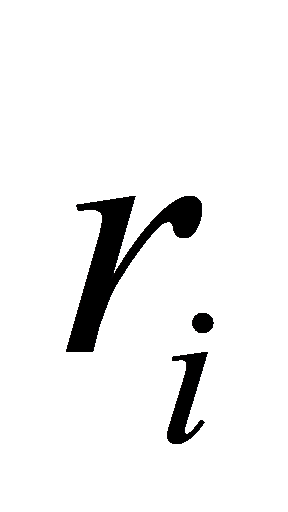are rational numbers that satisfy one of the following conditions:

1. The coefficient 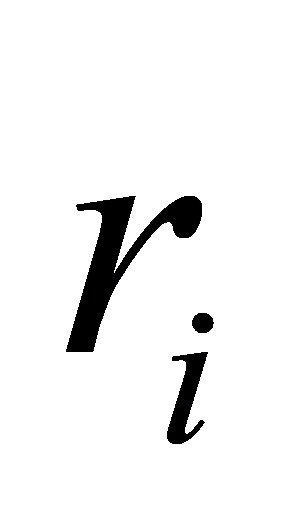is zero.

2. The coefficient 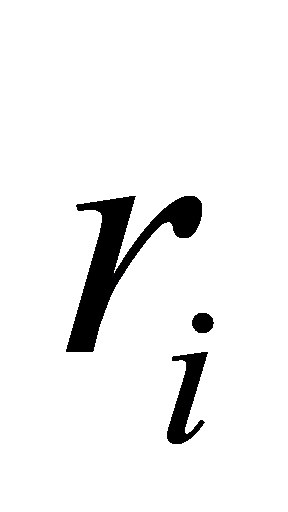is a nonzero rational number whose denominator is not divisible by the prime number \( p \) [9].

Every single rational number can be express as a single term of p-adic number. We can go further defining p-adic number and p-adic integer through p-adic series.

Definition 4.2 (p-adic number). Every p-aidc series represents a p-adic number, which is defined as a normalized p-adic series.

p-adic seris 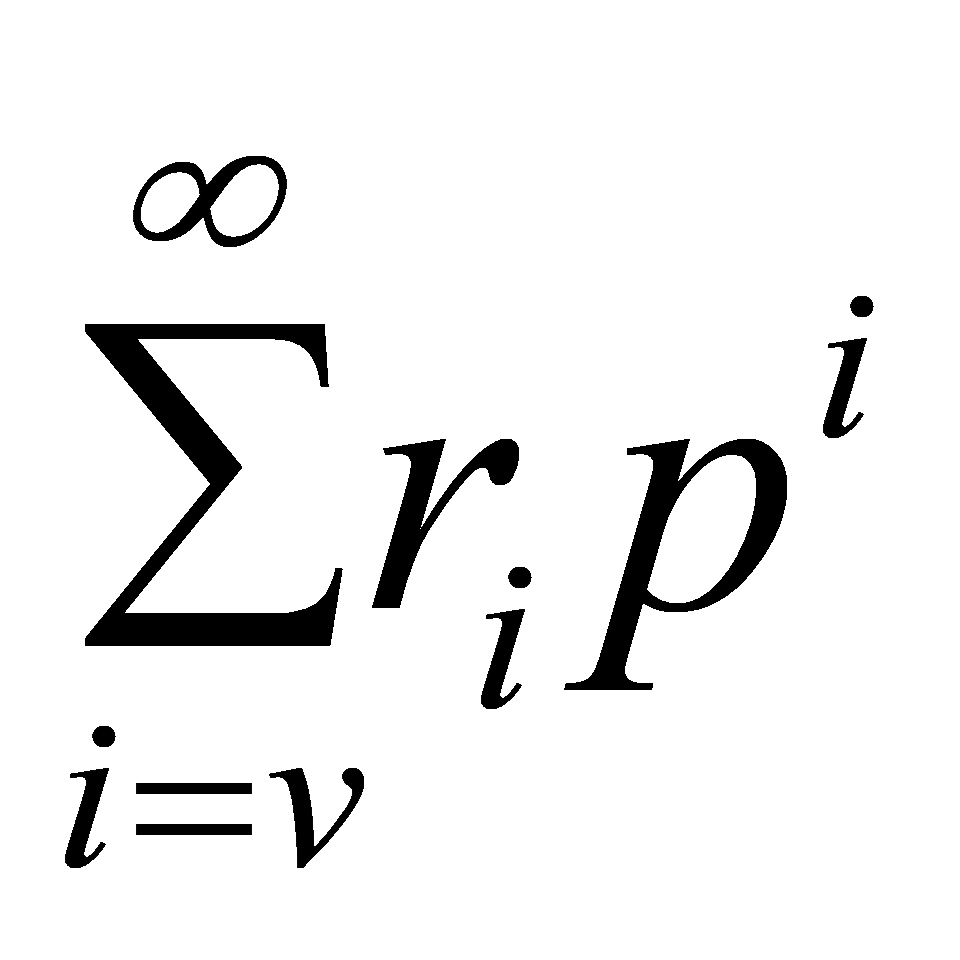is normalized if either all 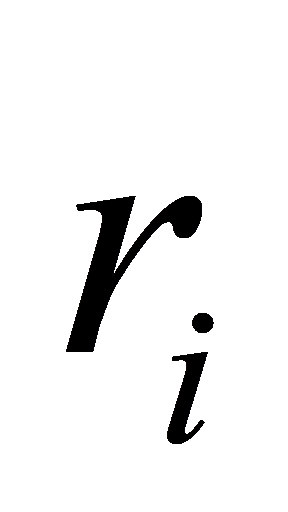are integers such that \( 0 ≤ ai \lt p, av \gt 0, \) or all \( ai \) are zero for all \( i \) . If all \( ai \) are zero then it is called zero series.

4.2. Zp

Definition 3.3 (p-adic integer). A p-adic integer α is defined by a sequence of integers \( xk \) that \( k ≥1 \) expressed as:

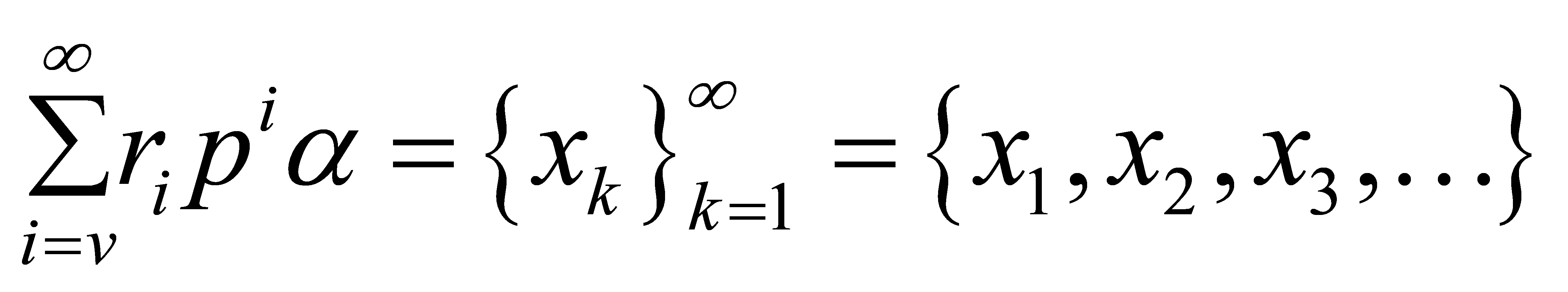.(8)

And it satisfies the condition below:

.(9)

Simply speaking, each term is congruent to the previous term in the sequence modulo power of \( k \) of 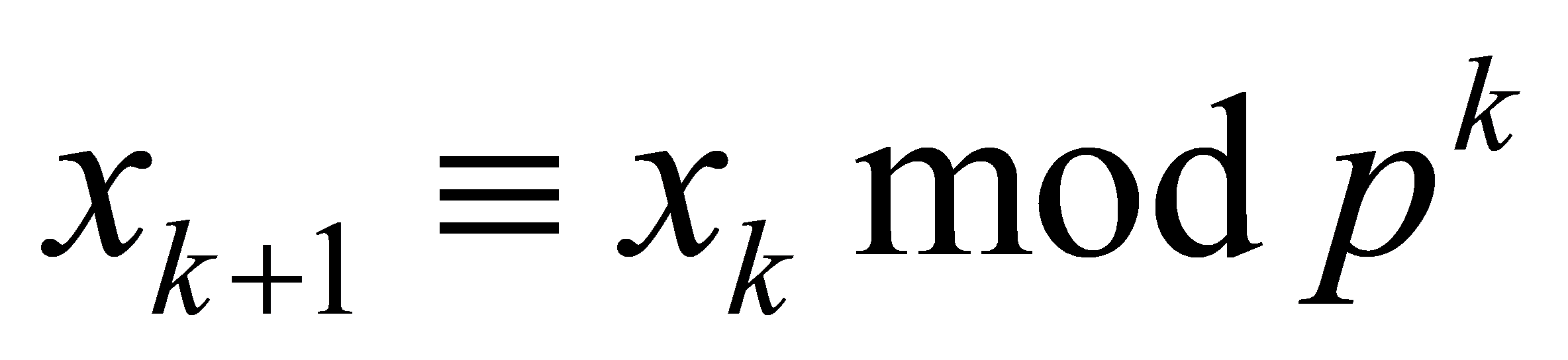the prime number \( p \) . Only if, two sequences \( \lbrace xk\rbrace \) and \( \lbrace yk\rbrace \) determine the same p-adic integer α if and for all \( k ≥ 1 \) : The set of all p-adic integers is denoted by \( Zp \) , and it consists of all sequences of integers satisfying these conditions. Every integer is a p-adic integer. The rational numbers in the form of \( (apk)/b \) with b coprime with p with \( k ≥ 0 \) are p-adic integers too [10].

Example 3.1. It can take p = 5. Here are several elements in \( Z5 \) :

\( α = \lbrace 36, 36, 36, ...\rbrace = \lbrace 1, 11, 36, 36, ...\rbrace , \)

\( β = \lbrace -1, -1, -1, ...\rbrace = \lbrace 4, 24, 124, ...\rbrace \) .(10)

There is another way to express a p-adic number. From the condition, 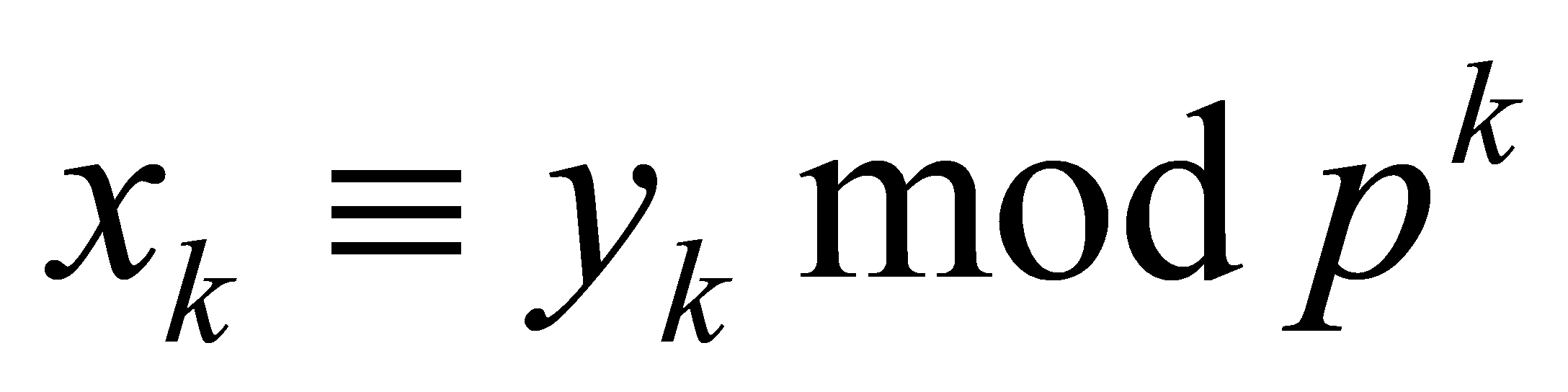, it can deduce that and where \( ai \) is integer 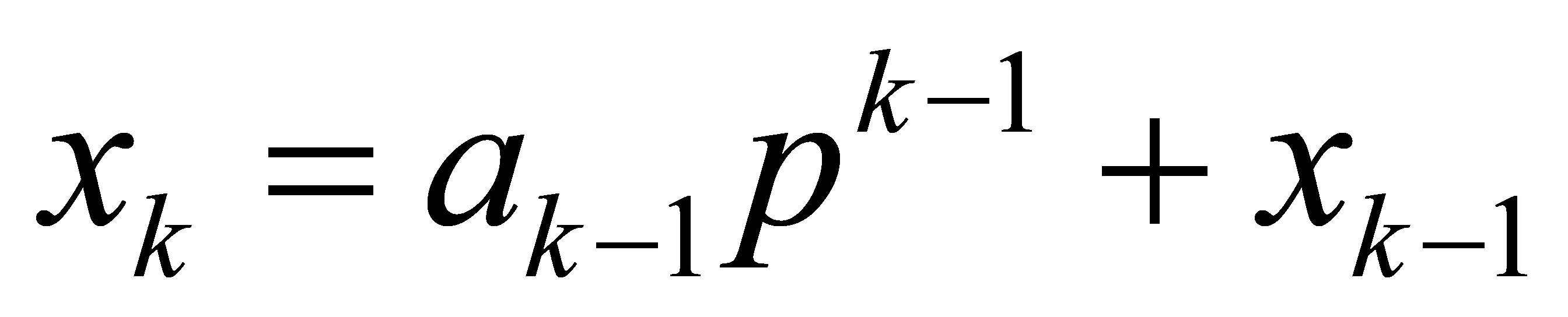, , 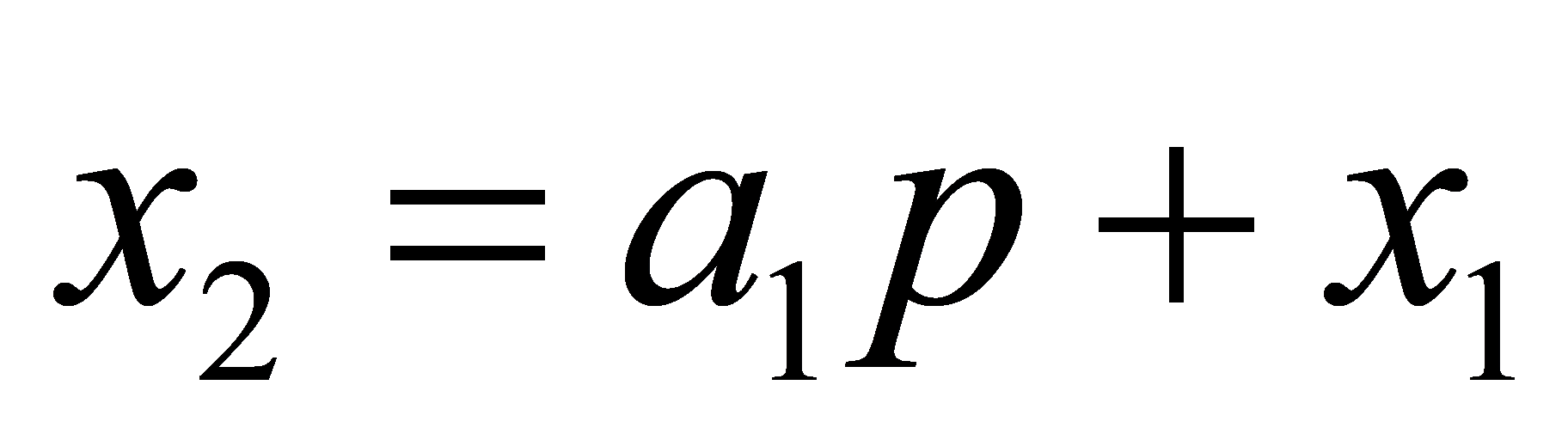and \( 0 \lt ai \lt p - 1 \) . The sequence \( ai \) is called p-adic digits. Then it can deduce that:

.(11)

For example 3.1, \( α = 36 = 1 + 2 × 5 + 1 × 52 \) , so the 5-adic digits are 1, 2, 1, 0, 0....

5. Properties of p-adic integer

5.1. Ring Z_p

By the multiplication and addition, it can find that \( (Zp, ·, +) \) form a commutative ring:

\( \lbrace xk\rbrace + \lbrace yk\rbrace = \lbrace xk + yk\rbrace ;\lbrace xk\rbrace · \lbrace yk\rbrace = \lbrace xk · yk\rbrace \) ,(12)

where \( xk \) and \( yk \) are p-adic integer. Here are several proposition of commutative ring \( Zp \) [1].

Proposition 5.1.1. \( Zp \) is an integral domain, which means \( Zp \) is a nonzero commutative ring that the product of two nonzero elements in the ring is nonzero.

Proposition 5.1.2. The p-adic numbers of valuation zero are the units of \( Zp \) . A unit u of a ring means that there exists v in the ring satisfies \( uv = vu = 1 \) .

Proposition 5.1.3. Let \( α = xk ∈ Zp \) . Then

,

.(13)

Proposition 5.1.4. \( Rp \) is a ring and \( Z ⊂ Rp ⊂ Zp, Z ⊂ Rp ⊂ Q \) . Then \( Rp = Zp ∩ Q \) .

5.2. Field Q_p

It can define a field under a fraction of p-adic integer since \( Zp \) can form a commutative ring.

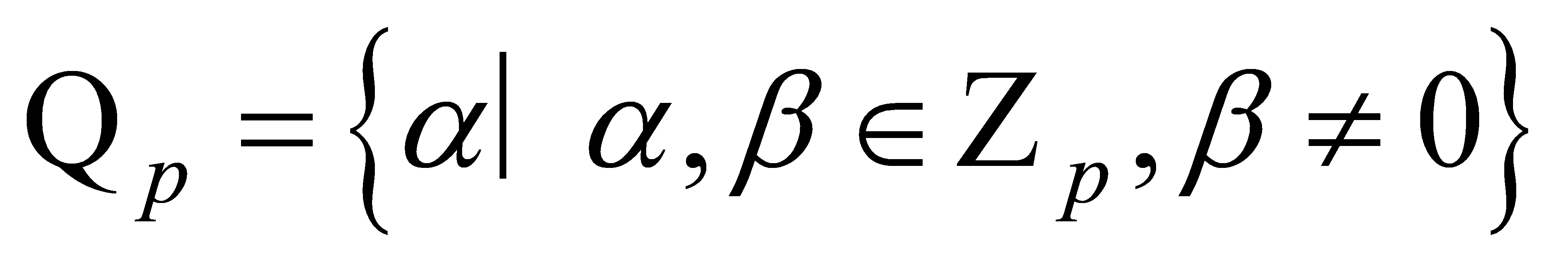,(14)

where \( Zp \) is a subring and \( Q \) is subfield.

Furthermore, it can also define a norm on the set \( Qp \) _.

Definition 5. 2 .1. Let p be prime integer. It can define p-adic norm of nonzero \( x ∈ Qp \) to be;

,(15)

where \( |0|p = 0 \) and \( vp \) is the valuation of \( x \) .

Here are several propositions for the p-adic norm [8].

Proposition 5.2.1. Strong triangle inequality is satisfied for each p-adic norm on \( Qp \) , meaning that for each x and y, \( |x + y|p ≤ max\lbrace |x|p,|y|p \rbrace \) .

Theorem 5.2.1. (Ostrowski’s theorem) exceptionally high absolute value standard for rational numbers Q is equivalent to a p-adic absolute value or the common real absolute value.

The idea of the theorem is that if the norm of any whole number is at least 1, then the size of any real number can be measured by raising its absolute value to some positive power. But if the size of a whole number is less than 1, then the least number n must to be the prime number p such that

(16)

6. Extention of p-adic numbers

p-adic number is not only useful in number theory but also in other fields. In theoretical physics, p-adic numbers have been used to explore certain aspects of string theory and quantum mechanics. They have been proposed as a framework for understanding the non-archimedean aspects of these theories. n computer science, p-adic numbers can be used in algorithms for solving various mathematical problems, including those related to number theory and cryptography. They can also be used in computer algebra systems for symbolic mathematics.

7. Conclusion

In summary, p-adic numbers grew out of a desire to delve deeper into number theory, and they provide a unique way of measuring numerical magnitude, especially in the presence of prime numbers. This unique perspective, rich in properties and applications, enables p-adic numbers to become valuable tools in fields ranging from number theory to cryptography, providing new insights and expanding our mathematical horizons. In essence, p-adic numbers embody the evolving nature of mathematics, constantly reshaping our understanding of numerical phenomena.