1. Introduction

In recent years, machine learning has become an indispensable tool in our daily lives, from recommendation systems in search engines [1] to computer vision for smart homes [2] and self-driving cars [3]. However, building successful machine learning services requires access to large quantities of high-quality training data. Unfortunately, certain data, such as medical records from hospitals or analytics data from personal devices, are protected by privacy laws (e.g., GDPR [4]) and cannot be readily used for training machine learning models. This lack of usable training data obstructs the development of valuable machine-learning services for domains such as healthcare.

Federated learning (FL) [5] has emerged as a promising approach to address this data privacy issue. In FL, multiple clients train machine learning models locally on their private datasets before sending the models to a federated server. On the server, the local models are aggregated into the global model. The global model is then distributed back to the clients for further training, completing the loop. The decentralized approach of FL ensures that raw data remains secure in its original locations, enabling privacy-preserving collaborative machine learning.

The current most popular FL aggregation algorithm is FedAvg [5], which averages the weights of all the local models to produce the global model. Despite its widespread use, FedAvg encounters challenges in scenarios where clients possess non-independent and non-identically distributed (non-IID) data. This is crucial because most data in the real world is non-IID [6]. For instance, medical data collected from hospitals in different geographical regions will significantly differ due to varying patient demographics and environmental factors. These kinds of non-IID data cause the local objectives of individual clients to be inconsistent with the global optima, impacting the accuracy and convergence of the global model [7].

Several efforts have been made to develop effective FL algorithms for non-IID data, including FedProx [8], FedNova [9], FedBN [10], CCVR [11], SkewScout [12], and SCAFFOLD [13]. In this paper, we take an alternative approach to address the non-IID challenge by proposing Mixed Data Calibration (MIDAC). MIDAC mixes \( M \) data points in clients' private datasets to neutralize sensitive information in each individual data point and uses the mixed data to calibrate the global model on the federated server in a privacy-preserving way.

MIDAC improves the accuracy, stability, and convergence speed of the global model while ensuring clients' privacy through mixed data encryption. This is achieved with minimal computational overhead, ensuring practical applicability. Furthermore, MIDAC's customizable calibration parameters allow for tailoring the privacy-utility trade-off to suit specific requirements, making it a versatile solution for various applications.

We conducted extensive experiments using the CIFAR-10 [14] and BloodMNIST [15] datasets to evaluate the effectiveness of MIDAC. Our results show that MIDAC consistently improves the accuracy of the global model aggregated using FedAvg. In this paper, we also assess the impacts of various calibration parameters, including the number of data points mixed, the number of calibration epochs, and the size of the calibration dataset.

The rest of this paper is organized as follows: Section 2 presents related works about non-IID federated learning. Section 3 provides background information on federated learning and the challenges posed by non-IID data. Section 4 introduces MIDAC, explaining its processes and privacy implications. Section 5 details the experiments evaluating MIDAC's effectiveness and the impact of various calibration parameters on its performance. Section 6 concludes the paper and discusses future research directions.

2. Related Works

There are existing studies seeking to find effective solutions to the non-IID challenge. These include FedProx [8], FedNova [9], FedBN [10], CCVR [11], SkewScout [12], and SCAFFOLD [13]. FedProx [8] introduces a framework extending FedAvg to handle statistical and systems heterogeneity, providing convergence guarantees and improved robustness. FedNova [9] introduces normalized averaging to mitigate convergence slowdown and solution bias caused by objective inconsistency in federated optimization. FedBN [10] uses local batch normalization to alleviate feature shift in non-IID scenarios. CCVR [11] focuses on learning with non-IID data by adjusting classifiers using virtual representations, resulting in improved classification performance. SkewScout [12] adapts communication frequency based on the accuracy loss caused by skewed data label distributions, mitigating accuracy loss. SCAFFOLD [13] corrects 'client-drift' in local updates with control variates, ensuring more stable and faster convergence compared to FedAvg. However, none of these methods have been shown to outperform all others comprehensively, and non-IID remains a foremost challenge for FL. No existing studies have proposed mixed-data calibration for non-IID scenarios.

3. Preliminary

Federated learning is a promising approach for privacy-preserving and collaborative machine learning on decentralized data across multiple clients. In Federated Learning, clients first independently train local models with their local datasets. After a certain number of epochs of local training, clients send their updated local models to the federated server for aggregation. The most popular method of aggregation is FedAvg [5], which averages all the local models into a single global model.

Let \( g(\cdot ) \) be the global model and \( {f_{k}}(\cdot ) \) be the local model of the \( k \) -th client trained with corresponding local dataset \( {D^{k}} \) . If there are \( K \) clients in total, global model aggregation according to FedAvg can be represented as,

\( g=\frac{\sum _{k=1}^{K}{f_{k}}(\cdot )}{K}. \) (1)

After aggregation, this global model is distributed to the clients to serve as their new local model. This cycle repeats for a designated number of rounds. Note that throughout this process, the local datasets never leave their clients, thereby preserving clients' data privacy.

3.1. The Non-IID Challenge

A notable impediment in federated learning is the presence of non-IID (non-independent and identically distributed) data across multiple clients. Non-IID data introduces significant challenges by inducing disparities in the local models trained on these diverse datasets, consequently degrading the performance of the global model. Disparities in the local models are primarily caused by the presence of drift in local training. This drift arises because of significant variations in the distribution of each local dataset, rendering the local objectives of individual parties inconsistent with the global optima [7]. Consequently, the accuracy of averaged model (i.e., the global model) \( g(\cdot ) \) is much lower than the average accuracy of local models \( {f_{1}}(\cdot ),{f_{2}}(\cdot ),…,{f_{k}}(\cdot ) \) .

\( Acc(g)≪\frac{\sum _{i=1}^{k}Acc({f_{i}})}{k}, \) (2)

where \( Acc(\cdot ) \) is the measurement of a model's accuracy.

4. Global Model Calibration with Mixed Data

We propose the method of MIxed DAta Calibration (MIDAC) to improve the performance of the global model while preserving the privacy of clients’ data. MIDAC improves the accuracy of the global model with low computational overhead and preserves sample-level privacy of clients' data.

Mixed data calibration adds three additional steps to the standard process of federated learning. After a client completes its local training, we take a portion of its data and encrypt them through mixing. Specifically, for the local dataset \( {D^{k}} \) on the \( k \) -th client, we randomly sample \( M \) images \( [{x_{1}},{x_{2}},…,{x_{M}}] \) from the \( c \) -th class and mix them by averaging their pixel values to generate a synthetic image \( \bar{x} \) , as seen in Fig. 1.

\( \bar{x}=\frac{\sum _{i=1}^{M}{x_{i}}}{M}. \) (3)

Clients generate \( N \) mixed images \( [\bar{{x_{1}}},\bar{{x_{2}}},…,\bar{{x_{N}}}] \) , and send them to the federated server along with their local model. Each round, on the federated server, we collect mixed images from all clients into a single dataset \( \bar{{D^{g}}} \) , consisting of \( [\bar{{x_{1}}},\bar{{x_{2}}},…,\bar{{x_{k\cdot N}}}] \) .

After global model aggregation according to FedAvg, we calibrate \( g(\cdot ) \) by training it with \( \bar{{D^{g}}} \) for \( T \) epochs.

\( g=arg{{min_{g}}}  {Σ_{i}}L(g(\bar{{x_{i}}}),{y_{i}}), (\bar{{x_{i}}},{y_{i}})∼\bar{{D^{g}}}. \) (4)

Fig. 2 is a visualization of our proposed method, MIDAC.

Privacy of Mixed Data. Privacy has a budget, and trade-offs are inherent in approaches aimed at maintaining privacy while effectively training high-accuracy models [6]. MIDAC seeks to find an optimal balance between privacy and effectiveness. To evaluate the privacy of mixed data, we categorized privacy into sample-level privacy and class-level privacy.

Sample-level privacy refers to the protection of sensitive or identifying information from individual data points, whereas class-level privacy refers to the protection of the class to which data points belong. For example, sample-level privacy would protect an image of a car from being identifiable by concealing information such as its color, brand, and license plate. Conversely, class-level privacy would prevent the image from being identifiable as belonging to the class “car.”

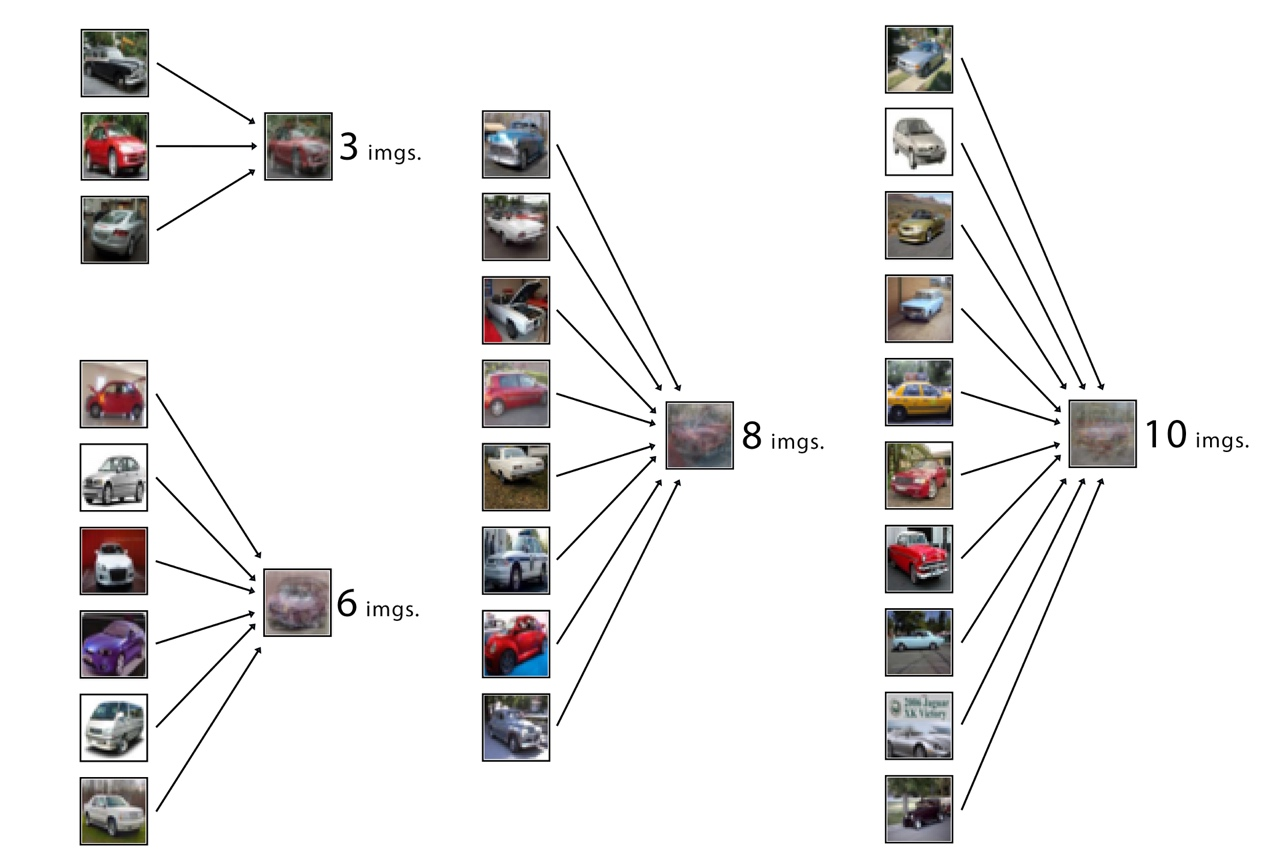
Figure 1. Mixing different (3, 6, 8, 10) numbers of real images into a single synthetic image.

Mixed data preserves the sample-level privacy of clients’ data. When \( M \) data points are mixed into a single mixed data point, any sensitive or identifying information from the original data points will no longer be accessible through the mixed data point. For example, a mixed image consisting of 10 similar X-ray scans of the lungs will not reveal any information that may compromise the identity of any of the patients. The encryption of mixed data can be strengthened by increasing \( M \) , the number of data points mixed into a single mixed data point, ensuring that the mixed data points are similar in size and shape, and adding random noise. In a survey we conducted on a group of 50 people, we found that people cannot recognize the identification of the original images from a mixed image consisting of 6 real images. Furthermore, current image separation approaches such as BSS (Blind Source Separation) [16] and BID (Blind Image Decomposition [17] are designed to separate distinct elements within images, such as an apple from a bee. However, they encounter significant obstacles when trying to separate many similar images deliberately mixed together.

Figure 2. Visualization of FedAvg with MIDAC, steps unique to MIDAC are bold and italicized. Compared to FedAvg, MIDAC generates synthetic images by mixing on the client side and uses the synthetic data to calibrate the global model.

Mixed data does not preserve class-level privacy. However, this will be acceptable in most scenarios since class-level information is often not inherently private. For example, a mixed image of X-ray scans of the lungs will reveal that the hospital from which the image originated performs X-ray scans on patients’ lungs. However, since this information is already easily accessible through regular means, it is not a breach of the hospital’s or its patients’ privacy.

5. Experiments

5.1. Setup

5.1.1. Datasets. We conduct experiments using the image datasets CIFAR-10 [14] and BloodMNIST [15]. We selected CIFAR-10 because of its widespread popularity and BloodMNIST to evaluate the performance of MIDAC in medical settings. We employ a Dirichlet distribution [18] to simulate non-IID data across 10 clients. \( α \) is a parameter of the Dirichlet distribution - a smaller \( α \) will result in a higher non-IID degree in the data. Fig. 3 visualizes a Dirichlet distribution ( \( α=0.5 \) ) of the CIFAR-10 training dataset (10 classes with 5000 data samples each) among 10 clients. Fg. 3 shows both the amount of data each client possesses, and the data distribution within each client is significantly varied.

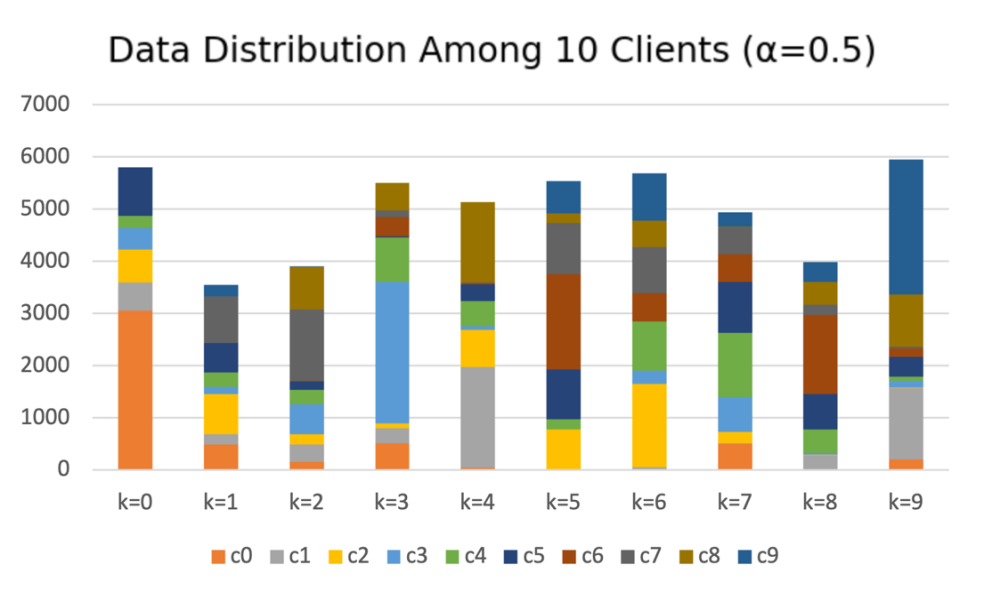
Figure 3. A Dirichlet distribution across ten clients. \( k \) represents clients and \( c \) represents classes. Each client has very different data distributions which faithfully simulates real world scenarios.

5.1.2. Models. We evaluate our method on VGG11 [19], ResNet18 [20], SimpleCNN, and MedCNN [15]. VGG11 and ResNet18 are deep neural network architectures widely utilized in various computer vision tasks; MedCNN is the model used to benchmark the BloodMNIST dataset in its original paper; And SimpleCNN is a lightweight CNN model we created for these experiments.

5.1.3. Training Hyper-parameters. We maintain consistent training hyper-parameters across all experiments. The number of local training epochs is 5, the local batch size is 32, and the local and global learning rate is both 0.01.

5.1.4. Calibration Hyper-parameters. We evaluate several adjustable calibration parameters in our experiments: including the number of images \( M \) constituting each synthetic mixed image, the number of synthetic images in the calibration dataset \( \bar{{D^{g}}} \) , the number of calibration epochs \( T \) , and the calibration learning rate \( {l_{c}} \) .

5.2. Improvement against regular FedAvg

In this subsection, we conduct a series of experiments evaluating the performance of FedAvg with MIDAC against regular FedAvg under the non-IID CIFAR-10 and BloodMNIST.

5.2.1. CIFAR-10. First, we conducted tests with the VGG11 model on non-IID CIFAR-10. In these tests, \( M=8 \) , \( T=1 \) , \( {l_{c}}=0.0001 \) , and \( \bar{{D^{g}}} \) contains 100 synthetic images per round (10 per class). According to Fig. 4, the MIDAC consistently exhibits around 2-3 percent higher accuracy compared to baseline FedAvg.

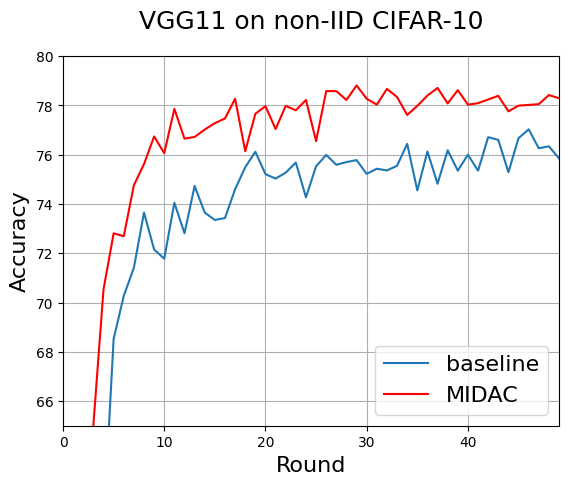
Figure 4. MIDAC outperforms the baseline across all rounds by about 2-3 percent accuracy using VGG11 on non-IID CIFAR-10.

Next, we conducted tests with the ResNet18 model on non-IID CIFAR-10 with the same calibration parameters. Fig. 5 shows that MIDAC consistently exhibits around 2 percent higher accuracy than the baseline. Combined with Fig. 4, we conclude that MIDAC consistently exhibits improved accuracy against FedAvg on popular model architectures.

Finally, we conducted tests with the SimpleCNN model on non-IID CIFAR10 under identical calibration parameters. Fig. 6 shows that MIDAC exhibits a significant 3-4 percent accuracy improvement over the baseline, showing that MIDAC flexible to both small and large models. However, Fig. 6 also shows the accuracy of MIDAC starts decreasing around round 15. The peak accuracy of MIDAC is 59.75 percent, while the accuracy at round 50 is only 58.2 percent. We believe this decrease is due to the simple nature of the SimpleCNN model, which may have resulted in overfitting. This analasys is supported the accuracy of the basline, which also begins decreasing around round 30.

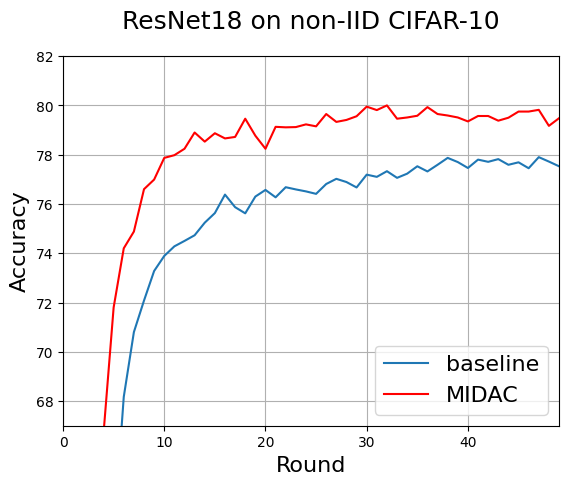
Figure 5. MIDAC outperforms the baseline across all rounds by about 2 percent accuracy using ResNet18 on non- IID CIFAR-10. Combined with Fig. 4, we conclude that MIDAC consistently exhibits improved accuracy against FedAvg on popular model architectures.

Figure 6. MIDAC outperforms the baseline across all rounds by about 3-4 percent accuracy using SimpleCNN on non-IID CIFAR-10. This shows MIDAC is flexible to both small and large models.

5.2.2. BloodMNIST. We conducted tests with the MedCNN model on non-IID BloodMNIST. In these tests, \( M=8 \) , \( T=1 \) , \( {l_{c}}=0.0001 \) , and \( \bar{{D^{g}}} \) contains 80 synthetic images per round (10 per class). Fig. 7 shows that MIDAC consistently exhibits 2-3 percent higher accuracy than the baseline. We conclude that MIDAC retains its advantage in medical scenarios, proving its real-world applicability.

Figure 7. MIDAC outperforms the baseline across all rounds by about 2-3 percent accuracy using MedCNN on non-IID BloodMNIST (a medical image dataset). MIDAC retains its advantage in medical scenarios, proving its real-world applicability.

5.3. Evaluating various Calibration Parameters

In this section, we evaluate the effects of various calibration parameters to determine the configurations that result in best performance. All experiments in this section were conducted with the VGG11 model on non-IID CIFAR10 with \( α= 0.5 \) .

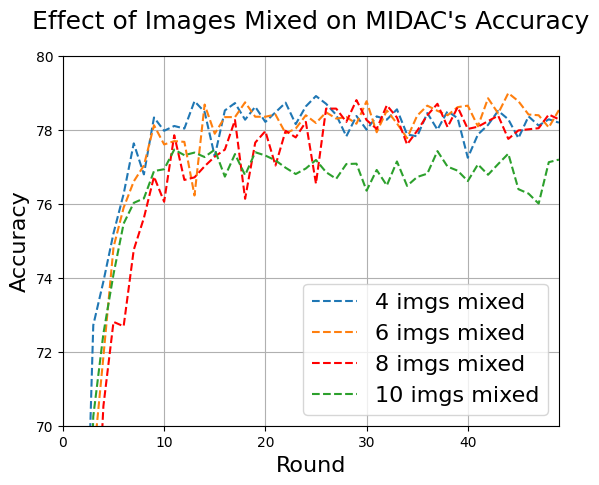
Figure 8. Accuracy of MIDAC using different numbers of real images for data mixing. 8 images are the most that can be mixed without compromising accuracy, which is why it is used for our other tests.

5.3.1. Number of Images Mixed per Synthetic Image. The more images \( M \) mixed per synthetic image, the stronger the encryption of mixed data. However, more images mixed could also result in lower accuracy. In this section, we conducted tests to evaluate how the number of images mixed \( M \) affects the accuracy of MIDAC. For all tests, \( {l_{c}}=0.0001 \) , and \( T=1 \) . We ran four tests at \( M=4 \) , \( M=6 \) , \( M=8 \) , and \( M=10 \) . Fig. 8 shows that \( M=4 \) , \( M=6 \) , and \( M=8 \) all converge at around 78 percent accuracy, whereas the accuracy of \( M=10 \) noticeably dropped to 77 percent. We conclude that 8 images are the most that can be mixed without compromising accuracy, which is why \( M=8 \) is used for our other tests.

5.3.2. Number of Calibration Epochs. We evaluated how the number of calibration epochs \( T \) affects the accuracy of MIDAC. In these tests, the \( M=8 \) , and \( l\_c=0.0001 \) . We ran three tests at \( T=1 \) , \( T=2 \) , and \( T=5 \) . Fig. 9 shows that the accuracy and stability decrease as the \( T \) increases. \( T=1 \) results in the highest accuracy. This may be due to overcalibration at higher epochs per round.

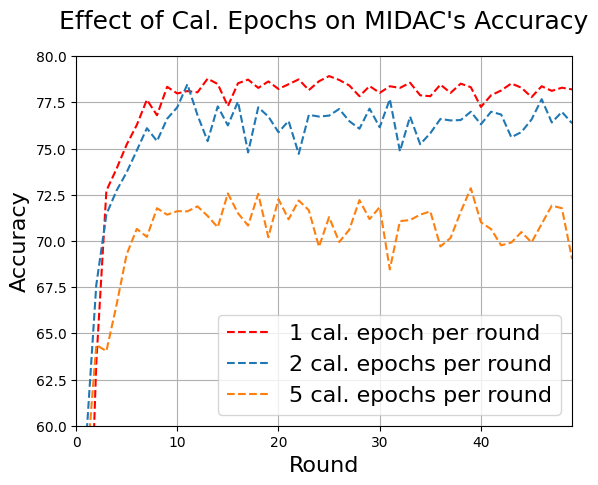
Figure 9. Accuracy of MIDAC using different numbers of calibration epochs per round on the server. Accuracy decreases as the number of calibration epochs per round increases. 1 calibration epoch per round exhibits the highest accuracy and stability.

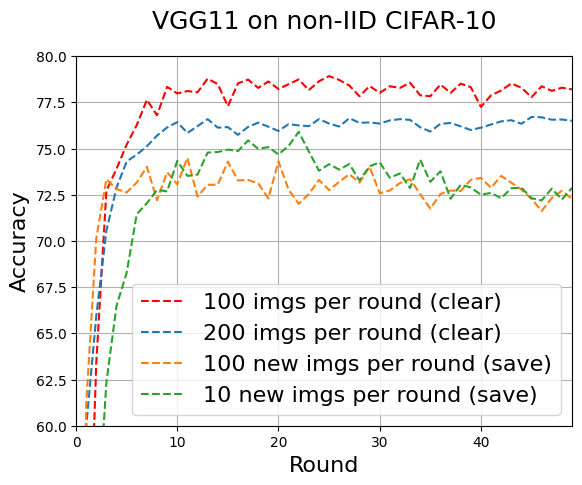
Figure 10. Accuracy of MIDAC with different mixed data utilization. Results show that accumulating synthetic data between rounds does not help.

5.3.3. Size of Calibration Dataset. We evaluated how the size of the calibration dataset affected the accuracy of MIDAC. In these tests, \( M=8 \) , \( T=1 \) , and \( l\_c=0.0001 \) . First, we tested adding 100 or 200 mixed images per round while clearing the calibration dataset at the end of each round. Fig. 10 show that 100 images per round (clear) exhibits around 1 percent higher accuracy than 200 images per round (clear) across all rounds. Next, we tested adding 10 or 100 new synthetic images to the calibration dataset per round while saving the calibration dataset at the end of each round. Fig. 10 also shows that clearing the calibration dataset between rounds results in higher accuracy and stability across all rounds compared to saving the calibration dataset between rounds. The accuracy at of 100 images per round (clear) is 5 percent higher than 100 new images per round (save) at round 50.

6. Conclusion

This paper introduced MIDAC, a method improving non-IID federated learning by calibrating the global model on server with privacy-preserving mixed data. Through extensive experiments on CIFAR-10 [14] and BloodMNIST [15] datasets, we have demonstrated the effectiveness of MIDAC in consistently improving the accuracy of FL models compared to the baseline FedAvg algorithm. Our experiments encompassed various model architectures, including VGG11 [19], ResNet18 [20], SimpleCNN, and MedCNN [15], showing that MIDAC is adaptable to different model sizes and domains, making it a versatile solution for non-IID FL scenarios. Moreover, we investigated the impact of key calibration parameters, such as the number of images mixed per synthetic image, the number of calibration epochs, and the size of the calibration dataset. These experiments provided insights into fine-tuning MIDAC for specific requirements and use cases. Regarding privacy considerations, our approach prioritizes sample-level privacy, ensuring that individual data points remain thoroughly protected by obfuscating sensitive or identifying information within mixed data points (we surveyed 50 people and researched existing image separation algorithms to confirm the security of mixed data). This commitment aligns with stringent privacy regulations like GDPR [4], making MIDAC a reliable choice for scenarios where individual privacy is paramount.

In summary, MIDAC presents a promising avenue for enhancing FL in real-world scenarios where non-IID data distributions are prevalent. Its practical applicability, demonstrated through experiments, underscores its potential to unlock valuable machine-learning services while safeguarding data privacy. Future research can focus on evaluating the performance of MIDAC with non-image data and exploring additional privacy-enhancing techniques.