1.Introduction

Service deployments to the cloud and the use of artificial intelligence are exponentially increasing the volume of data in the network. Along with the surge in demand for computing power, the widely used cloud computing framework is also facing enormous challenges, such as poor transmission, calculated immobility, and unstable storage. For this reason, Shi proposed that the algorithm model could be sunk to the edge [1]. As the emergence of edge computing, which can solve some problems caused by the massive data transmission to the server center, such as bandwidth shortage, network congestion, and long delay. However, due to the limitation of hardware, the edge side usually has insufficient computing power, time-consuming, and unmanageable data scattering problems when performing time-series data prediction such as affective computing. In order to obtain a valid model and still ensure the security of users' private data, Google proposed the Federal Learning (FL) paradigm [2]. FL enables servers and client devices to jointly build a shared model without sharing data, pass intermediate parameters through shared encryption, and construct an optimal model. FL typically involves a multi-round of communication between the server and the clients (i.e., mobile devices), where in each round, participants first use their own limited size data to train their models[3]. And then, the central server aggregates these participants' models into an integrated, global model. FL paradigm consists of client-server architecture and decentralized architecture [4], more analysis of centralized architectures in various studies, because of the privacy [5], saving resources, and high availability. Affective computing requires a lot of engineering to go from physiological data to recognizing emotions, which will consume a long time, and human-computer interaction needs to reduce the time required for computing. Human physiological data is more sensitive data, which can be analyze not only for emotions but also for a lot of information about human privacy. There is an urgent need to find new ideas to solve these problems in affective computing, and federal learning can be a good way to deal with the dilemmas facing affective computing.

However, FL still needs to work on the following problems. On the one hand, due to the chain law, each participant's available computational resources are not the same. And the network bandwidth changes all the time, which results in the participants must train the model at different times. As a result, the consumption time during the training of the federated model becomes unstable, which will be more problematic in dealing with task scenarios that require high timeliness, such as autopilot and man-machine interactive. On the other hand, clients cannot always have sufficient computing resources to train online. The training of the entire model will be impacted if a participant unexpectedly fails, and the amount of data transferred during training is too large. Thus, how to aggregate the clients’ model quickly and effectively determines the pros and cons of the FL model mainly. Furthermore, the quality and quantity of data are owned differently by each participant.

Affective computing is an important direction to enhance human-computer interaction, but it is facing the problem that emotion recognition is still too slow for human perception. If affective computing is run in a high-performance framework like FL, Training will be faster and more effective. There are two traditional approaches to sentiment computing: the first is to design one model per user, and the second is to share one model across all users. FL is a combination of two approaches to affective computing that takes into account the differences in individual physiological signals and also solves the dilemma of a single machine having difficulty maintaining multiple models. And FL will protect privacy better due to the encryption of the transmitted data.

Therefore, to make the FL more efficient and collaborative, and address the problems of affective computing due to slow feedback, online emotion recognition can be challenging in HCI scenarios, our work has optimized the training process of federation learning. Developed a provably effective FL algorithm to address the aforementioned system challenges. Furthermore, we improved the overall framework of FL. To predict the computing resources required for computing tasks, we proposed an algorithm model to estimate computing power. Owing to the algorithm model, the FL process selects the appropriate participant machine for a different task. Moreover, model correlation coefficients are used to calculate the similarity of each model parameter to eliminate participants that do not contribute positively to training in the model aggregation phase. Then, the computation delay of each participant model is estimated in the model update phase. Finally, bayesian maximum posterior estimation is invoked to calculate the probability of different clients’ participation in aggregation, and we proposed the loss-delay variable ratio as a weight for parameter updates. By assigning different weights, these approaches can train the optimal algorithmic model and reduce the model aggregation time. Here we optimized an FL model which both converges quickly and ensures the stability of the training process, by using increasing the weight coefficients to prevent model overfitting, and reducing training time, clients with sufficient arithmetic resources are selected. Importantly, using greedy strategies and intelligent algorithms, our entire time-domain optimized FL model achieves effective results, which effectively solves the problem of affective computing timeliness.

The paper is organized as follows: Section 2 reviews the literature related to FL analysis. Section 3 describes the optimized Federated Learning Algorithm for Time Domain Optimization in this paper. The method proposed in this paper is described in detail, as well as the principle analysis. Section 4, based on the same dataset and different devices for affective computing, uses the official dataset to validate the pros and cons of the proposed methods. Finally, Sections 5 and 6 present the results and conclusions of the experiments generated during this study.

2.Relate Work

2.1.Current status of research

FL is an emerging distributed learning technique. FL can deal with the issue of non-IID (not identically and independently distributed) data and data heterogeneity, which is different from distributed computing. It intends to jointly train shared models on various client devices by using client private data while maintaining data privacy. The traditional FL has six steps (Figure.1), which contain client device selection, server initialization of model parameters with model distribution, local training, parameter aggregation, and parameter update [6]. FL is generally divided into longitudinal FL, horizontal FL, federated reinforcement learning, federated migration learning [7], and hybrid FL. Horizontal FL is the learning within participating subjects, where the feature overlap is large and the sample overlap is small. But the longitudinal FL is the reverse. Federal migration learning means that the feature overlap and sample overlap are small between multiple parties participating in joint training. What’s more, many enterprise-level FLs are also gradually entering our vision currently, such as the self-developed enterprise-level FL platform FATE [8] (federated AI technology enabler) proposed in 2019.

A. K. Sahu et al [9] investigates federated learning in the context of non-IID data. The authors propose an algorithm called FedAvg, which addresses the challenges posed by non-IID data by introducing data weighting and local training epochs. Experimental results demonstrate that FedAvg achieves better performance than traditional federated learning algorithms on non-IID data. [10] X. Li et al tackles the non-IID data challenge in federated learning and presents a method called Statistical Distillation to improve performance. The approach utilizes statistical information to estimate the global data distribution and incorporates it into model training. Experimental results show that Statistical Distillation improves model generalization on non-IID data. There are many studies that show that FL can efficiently process Non-IID data.

FL is gradually catching the attention of researchers. Most of them focus on designing different federation training strategies. In order to prevent the client model from entering a local optimal scenario, hence the FedProx [11] method is incorporated as a solver to control the update rounds of the client, accelerating the convergence of the federated global model. In this paper, we presented an analysis of the possible cases of local optimal. Li et al. proposed FedBN [12], which adds a batch normalization layer (BN) to the local model, to solve the feature shift in the heterogeneity of federated learning data. Although these studies can speed up convergence, they neglect to consider communication costs and imbalances in training data distribution among participants. FedNova [13] standardizes client update methods to solve the difficulties of inconsistent client data. Cao et al. [14] proposed a distributed deep-learning framework to deal with privacy preservation and parallel training issues. This framework proposes a goodness function, where the function value is defined according to the client dataset size and the loss value. Clients upload the value of the goodness functions to the server, and the server selects the client to upload its model parameters based on the size of the goodness value. Selecting participants with higher accuracy to upload model parameters can effectively avoid inconsistent data distribution and speed up the convergence of the model. However, this method will waste data. As each participant's data will contribute to the final model, the selection of participants to update the central model parameters requires further consideration.

In addition, many researchers have focused on data communication issues. Chen et al. [15] proposed to reduce communication costs by optimizing FL training and communication frameworks. Goetz et al. [16] proposed an Active Federated Learning(AFL) framework, each client executes a value evaluation function and then uploads the result to the server. Based on the result, the server calculates the probability of the client participating in the next model training and selects the participants. The above methods have high requirements on the rationality of the function, and do not consider important factors such as the computing power and data quality of the participants. Blindly adding functions will greatly increase the calculation amount of FL and bring unnecessary model complexity. In terms of model aggregation, Yurochkin et al. proposed a Bayesian nonparametric approach [17], which matches client weights before aggregating parameters. FEDMA [18] further optimizes it through iterative inter-layer matching. Yet, the calculation and communication of FEDMA have a linear dependence on the network, and it is not suitable for training deeper models. In our paper, we use posterior probability and model similarity methods to address this problem exactly. Federalization of models is also an important branch of FL research. It usually considers models with less arithmetic power consumption, such as MobileNet [19]. Alternatively, the model can be de-branched, for instance using an 8-bit integer (INT8) instead of 32-bit floating point (FP32) precision for training and inference, which reduces the model size, and simplifies the data manipulation steps. Among them, extreme quantization uses 1 bit to represent network weights and activations, known as binarization [20]. Using Knowledge Distillation (KD), the complex teacher network is compressed into a sparser network model that performs similarly to the teacher model.

In summary, FL has a good performance in reducing model training time and increasing data security. New computing architectures are gradually attracting interest in affective computing, [21] proposed Edge AI technology to analyze thermal imaging image data of buildings, for rapid analysis of building house occupancy information, compared to traditional AI techniques, this approach offers a significant improvement in the time dimension. [22] the authors proposed Smart Edgent, a collaborative on-demand DNN co-inference framework with device edge synergy, that can split the network to another device, which Co-training models, and runs the network faster. We use FL to train the model, and through FL to solve the problem of high time-consuming affective computing.

2.2.Our contribution

Focusing on the modification of the model can reduce the training time of FL as well as the communication cost, and calculation amount, but the model's accuracy will suffer. Here we focus on three aspects of communication costs, computational efficiency, and incentives to reduce the time required for federation learning training and reduce the amount of computation, optimize the federation learning process. Assuring federated learning is rational and effective, using greedy strategies combined with algorithms can improve efficiency.

3.Methodology

3.1.Traditional Federal Learning

Suppose there are M client devices in federated learning, the collection of client devices is represented as\( M=\lbrace 1,2,…,K\rbrace \), where\( m∈M \)denoting a client device. Assume that each participant’s device is independent and can communicate smoothly with each other. Realistically, each client device has a distinct level of computer capability. Computer capability is expressed by equation (1) [23].

The concept of FLOPS was first proposed by Frank H. McMahon [24]. FLOPS is the number of floating-point operations performed per second, which is a measure of computer performance. In this study, FLOPS is used to define computational capability. Usually, FL takes all client devices into account, or selects them in a random way, when the device’s CPU resources are insufficient to execute the algorithmic model or when network bandwidth resources are limited, this slows down the overall FL framework.

3.1.1.Participating Device Selection. The computing resources required by federated learning's algorithm model can be quantified\( {C_{k}} \), and the maximum resources available for each client device\( {R_{m}} \), then when the storage and computational resources are satisfied, the computational delay can be expressed as(2)[25]:

In the case of a stable network, we can assume that the delay may be larger when\( {T_{m,c}} \)is less than 1. On the contrary, the larger\( {T_{m,c}} \)the smaller the delay

It’s assumed that the loss value of the model is\( {L_{m}} \). Then, clients set the loss function as (3).

Where\( x \)is the training data of the clients,\( {y_{i }} \)is the true label,\( {y_{t}} \)is the prediction label , and\( D(x,y) \)represents the model. According to greedy theory, we can estimate the contribution of each participant model to the central model when it is aggregated (4).

Indicates the aggregation weight. The smaller the loss value, the higher the training degree of the model. FL can be effectively improved if the running delay is smaller. Thus, in the participant selection stage, if the resources required by the algorithm model are fully considered, and the resources and network bandwidth that each participant can provide. It not only speeds up the convergence of the algorithm model, reduces the time required for FL training, but also ensures the stability of federated learning.

3.1.2.Model training and parameter aggregation. Before distributing the model, initialize the algorithm model parameters to\( w(0) \), and each participant uses local data to train their own model. When the loss values of each participant tend to balance, the model stops training. FL enters the parameter aggregation step, and the commonly used aggregation methods are: Firstly, the weights of each participant are averaged, and the central model parameters after aggregation are (5).

where indicates the t-th training session.

Update the central server global parameters to. The participant continues to local training if the model does not converge. However, each participant's model training effect differs due to the different data resources. If all participantsdirectly update the model parameters in an average way, some better client models will be ignored. The federated learning model will converge slowly if too much weight is given to poorly trained models. We propose a method for evaluating model training that assigns different contribution coefficients to different participants, improving the recognition accuracy of the model as well as making it more effective.

3.1.3.Central Model update. In traditional federated learning, the update process of the central model parameters is as follows.

It’s assumed that equation (6) denotes the training data owned by the i-th participant, where\( w \)is the weight of the current global model, and the participants\( k \)run the step stochastic gradient descent with step length set to\( η \)(take 0.01,0.5,0.1), then the weight coefficients are iterated as in (7).

Where\( Δ\bar{l} \)denotes the average loss value of all clients,\( D{t_{i}} \)indicates the delay of the i-th participants in this round. However, in a real-world setting, the central server treats all participants equally, and the data input by each participant may be non-IID. If parameters are updated this way,\( ω \)may deviate[24],significantly affecting training model performance. Therefore, in the case of non-IID data, we need to assign different weight coefficients to each participant based on some parameters for updating the central model coefficients.

3.2.Optimized Personalized Federal Learning

To solve the problems encountered in the above process, this study proposes an innovative solution to break through the current dilemma of FL. It makes the FL training process more stable, reduces the training latency, and improves the effectiveness of training models.

3.2.1.Algorithm Model Arithmetic Prediction. Usually, in model training, it contains matrix multiplication and division, vector multiplication by matrix, and addition and subtraction of matrices. Here, FLOPs (floating point operations, floating point operations, understood as the amount of calculation) is used to measure the amount of calculation. Assume that the dimension of the input vector is\( {N_{n×n}} \), and the dimension of the hidden layer is\( a×n \), the state layer vector dimension is\( {M_{n×m}} \),then the number of calculations for a vector multiplied by a matrix is\( n×n \), the vector has columns\( 2n \), the number of calculations is\( 2{n^{2}} \). In the same way, multiplying a vector by a matrix is approximately\( {n^{3}} \),the vectors' total addition is around\( n \).Therefore, the number of calculations of neural network neurons after a gradient descent is equation (8).

When the matrix storage requires an average of 4B a number, the neuron needs\( 4×(2{n^{3}}+{n^{2}})B \)FLOPS memory to perform a gradient descent. From this we can estimate how much memory space is required to run a deep neural network. The data in the matrix are all floating-point types, and the stored input values are shown in equation (1), calculating the t epoch is expressed by equation (9) where\( num \)is the number of neurons.

In comparison to large-scale neural networks, machine learning models require less computation. Its main computational focus is on the extraction of features. By assuming an average calculation amount of\( 2{n^{3}} \)for each feature extraction, we can directly estimate the number of matrix multiplications, we can get the memory space and storage space required for the model. Support vector machines as in equation (10).

Where\( α \)is the step size, and\( b \)is the bias, the computational resources required for one iteration are\( a{n^{4}}×4FLOPs \). The larger the n size, the greater the memory resources required to run it once. However, the computing capabilities for extracting eigenvalues account for the majority and which needs to be estimated in detail. Knowing the computing resources required to run the model, it is also necessary to calculate the resources that each participant can provide. Here it is represented by equation (1). From the CPU model, we can determine the general computing power of the CPU. High-performance computing capabilities are represented by GPUs. In order to represent the arithmetic capabilities of the participants, we uniformly use CPUs since they are all end-side devices and not all GPUs are present. The storage capacity is expressed as hard disk space, and the network capacity is expressed as bandwidth.

3.2.2.Edge device selection. The above data indicate that when selecting participants for the central server, it is necessary to estimate the maximum amount of memory the algorithm model needs, which is verified by Table 1 [26]. Make sure the machine has more memory than the algorithm requires. Then, sort the devices by their storage capacity and network capacities, and select a participant with the higher ranking. In this way, we can avoid slowed-down federation learning due to the insufficient resources of some participants, insufficient network bandwidth, and other factors. This can guarantee the smooth progress of the FL and the stability of the model, and it can also speed up the efficiency of the federation learning.

The amount of data, and data quality varies across participants in affective computing, selecting participants for model training in this way allows the selection of participants with better equipment parameters. And remove the effect of noise on the model, ensuring smooth affective computing.

Table 1. Intel mainstream CPUS server computing

3.2.3.Training and parameter aggregation. Each participant receives the initial model from the central server after the parameters are initialized. Participants input their own data into the model network, train their own models, and execute the gradient update formula as equation (11).

where\( {ω_{k}} \)is the model parameter of the k-th client,\( ∇g({ω_{k}},{b_{i}}) \)is the derivative of the loss function,\( η \)is the update step, and\( {b_{i}} \)is the bias. The model stopped training when the loss values stabilized. In order to determine the pros and cons of each participant’s training model, the model parameters with the lowest loss values were extracted and denoted as equation (12):

Since the calculation of the correlation coefficient between model parameters is very computationally intensive, the correlation coefficient will be calculated each time the loss value decreases, thereby reducing the computational complexity of the algorithm. The correlation coefficient between each participant and the minimum loss value model is obtained, expressed as (13):

Where\( \bar{W} \)denotes the average value of the weights. With this value, when the calculation task reselects the aggregation node, based on Pearson and Bayesian theorem to determine the probability of each participant being selected to participate in the aggregation next time express as equation (14):

For each aggregation, the one with the larger probability value is selected as the aggregation parameter. The correlation coefficients of each participant's model parameters and loss value are used to select the participants for aggregation. Firstly, participants who may have a negative impact on the entire model recognition due to poor data quality are eliminated, and secondly, the model convergence is accelerated by a theory similar to greedy thinking, thereby realizing the optimization of the federated learning accuracy dimension.

Physiological data are all non-IID relationships in affective computing, the distribution of emotional data varies by age, gender and region. Selecting participants for aggregation in this way ensures a high degree of data similarity among participants involved in aggregation, thus, indirectly improving the accuracy of the central model and reducing the time for affective computing.

3.3.Model update strategy for assigning weights

By updating the parameters using the mean method according to the avgFL(Average Federal Learning), the entire algorithm model may deviate too much, and this will result in unnecessary calculations generated by federated learning. By taking into account the training effectiveness and response time of each participant model, the better performing participant model can be effectively selected and assigned a higher weighting. Poorer performers are assigned less weight. Here the model loss value\( F_{k}^{ \prime }(w) \)is used to measure the model. Response time is also an essential factor in speeding up model convergence. The overall feedback time t is the maximum value of the running time of each participant model plus the communication time in FL. The weight given to the participant model is also particularly important in the optimized federated learning model. We propose that the weight parameter can be expressed as (15):

\( Δ\bar{l} \)is the average loss value of all participants, and\( D{t_{i}} \)is the i-th round training delay, aggregating the central model parameters as (16):

According to the weight, the difference of each participant's data over time is obtained. If the updated global parameters of the central server did not converge, participants underwent the next round of local training. Therefore, the objective function is (17)[27].

Where\( G(f) \)represents the central model,\( f(x) \)represents the local model,\( i \)represents the i-th training round, represents the training data set, and\( λ \)represents the weight value. The central server decides whether to stop training based on the comparison of loss functions. After (17) is satisfied, the training is stopped and the model is successfully trained. Where\( F(ω) \)is the current loss value of the central server and\( f_{k}^{ \prime }(ω) \)is the loss value of the last training round of the k-th participant. The entire training process is outlined in Figure 1 below.

The entire optimized FL algorithm process can be expressed as algorithm 1 and algorithm 2.

Table 2. Heterogeneous federated learning algorithm for time domain optimization.

Firstly, 1-2 calculates the computing power possessed by the participants, and 3-4 extracts the model parameters of the participants' local models and perform model similarity calculation with the best performing model in this training round. 5–9 are the probabilities that the current iteration will participate in aggregation by model similarity. 9-10 are the values of sending own delay and loss, which are used as weight values for parameter updates by the central server.

Table 3. Personality federated learning algorithm for time domain optimization for central server.

1-3 Selecting Computationally Appropriate Participants for Greedy Strategies, 4-5 are the participants with better performance (loss value/computation delay) selected for parameter update, and 6-7 are central model parameter updates.

Based on the weight coefficients of the participants, the central server determines the loss function (18).

Which\( \frac{{D_{k}}}{D} \)is the weight coefficient of the k-th participant.

Participants' loss values represent their performance on the training model. And the latency of the participants' feedback to the central server indicates the timeliness of the training. Considering these two values into the parameter update of the model can create an effective balance between timeliness and accuracy. Using this method, the service timeout is avoided due to the high accuracy, which is time-consuming to calculate, but also the problem of fast calculation but low accuracy is also resolved. A good balance has been made between model accuracy and training time, which improves the scientific nature and stability of federated learning.

4.Experiments

4.1.Dataset, model and setup

We chose the publicly available affective compute dataset AMIGOS [28] to validate the feasibility, and advantages of the optimized FL paradigm. Electroencephalographic (EEG) signals were recorded by AMIGOS utilizing a 14-channel Emotiv Epoc wireless headset, while frontal video (RGB) and peripheral physiological signals were captured using a non-invasive device. Recording using the MAHNOB-HCI [29] dataset as the stimulus source. The dataset included both individual and group settings. 40 participants saw 16 brief movies (250s in length), but the second dataset, 17 individuals watched extended videos (>14 min in length) in both an individual and group setting. A total of 12,580 video clips were annotated (340 clips from 37 participants in both short- and long-video experiments). The arousal and valence used for these annotations were based on the SAM mood rating scale [30], which is from 1 (low arousal and low valence) to 9 (high arousal and high valence).

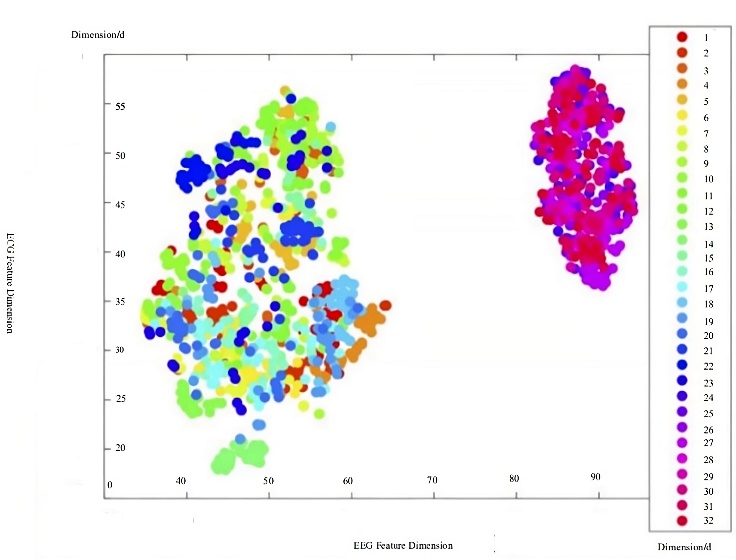
There were 800 records in the dataset. As shown in Figure 2, data labels can be divided into four states by coarsening arousal and validity into binary labels (positive and negative) with a separation point of 5. Due to the difference in the physical state of each person, when the physiological signal data of the subject is sent to each participant separately, the data set is IID, because each machine processes only the physiological signals of a single person, whereas when the data is processed on the same machine, it is non-IID, it is because the data contain physiological signals of multiple individuals, and the physiological signals of individual subjects are Non-IID. Here, we used EEG and ECG collected from single-person short videos as training data, and the dichotomy method for emotion recognition. In order to fully reflect the characteristics of the optimized federated learning, we selected two commonly used emotion recognition models for experiments, which are deep neural network and SVM. According to the calculation method in Chapter 3, the deep neural network is set to a 6-layer structure [31], and it can be predicted that the required memory is 862M FLOPs, the support vector machine algorithm [32] estimates that the required memory is 364M FLOPs. Using machine learning methods, extract time-domain features, frequency-domain features and nonlinear features of physiological signals, such as EEG and ECG. The number of features extracted for each participant is shown in Figure 3.

The experimental environment is three computers and one server, the configuration is shown in table 2. Using the server, participants are selected and intermediate variables are calculated, acting as the central model placement. Based on physiological signal data volume, use the virtualization software (VM WorkStation) to virtualize the three computers into 15 virtual machines with 0.8G FLOPs, 1G FLOPs, 1.5G FLOPs of memory, and 1G or 1.5G disk space. The specific configuration is shown in Table 4.

Table 4. Information on the configuration of the central equipment used for the experiment.

Table 5. Configuration information of the participant devices used for the experiment.

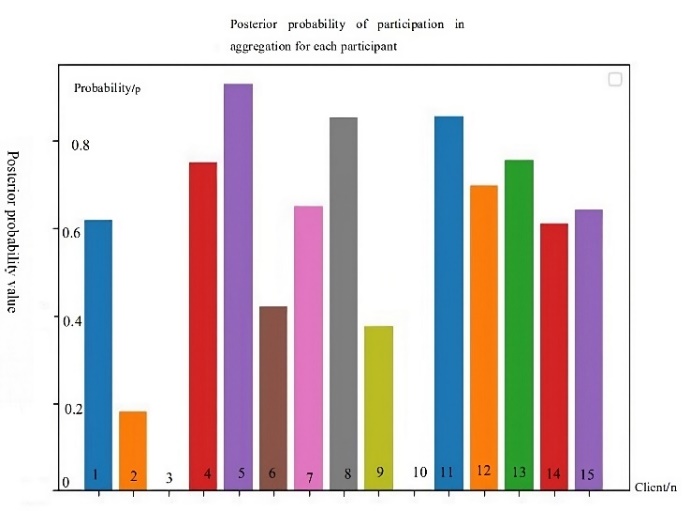
According to the method proposed in Section 3, iteration by stochastic gradient descent, the value of are set to (0.05,0.1,0.15), and the loss function is Equation (3-13) . With a sliding window of 3s to intercept the data, each window has (3*128*14) data. Select 80% of each data as the training set and 20% as the validation set for a 5-fold cross-validation. Therefore, the corresponding minimum loss after each measured participant's first stage run is 0.632, and according to the matrix of model parameters of this participant and the model parameters of other participants, the posterior probability of each participant joining the aggregation can be calculated by bringing into equation (11) the result as in Fig. 4.

4.2.Result Analysis

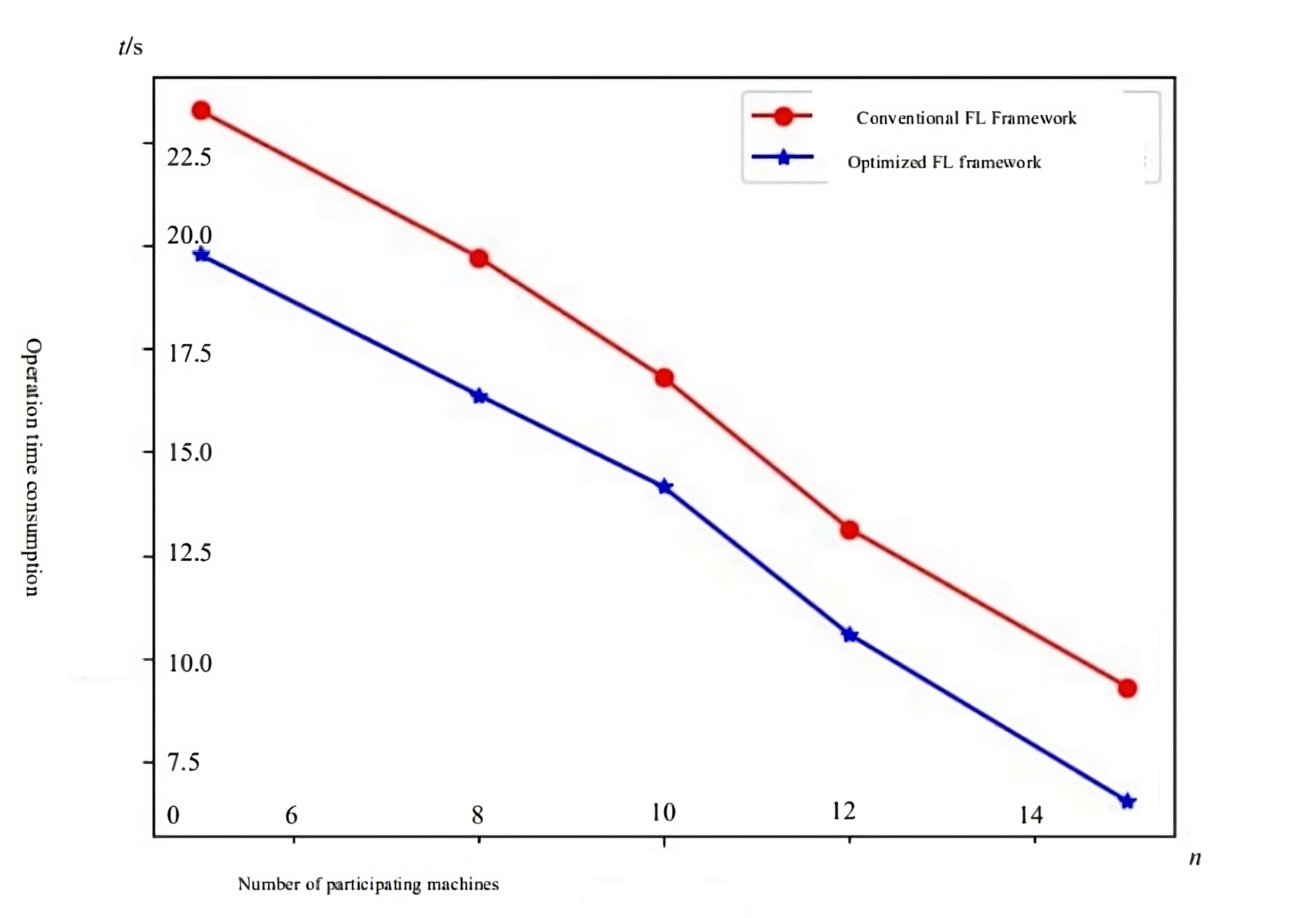
After the training of FL, 20% of the data was used as the validation set, and the recognition accuracy and training time were compared with traditional FL in the time domain dimension, and the results performed as in Figure 5.

From figure 5, the proposed FL framework in this paper has a greater advantage in model training timeliness compared to conventional FL. The reason for this is that while the goal of conventional FL is to train a global model, optimized FL considers that a single global model is difficult to converge and does not perform well on every client. The suggested aggregate, assessed in terms of Pearson Correlation coefficients, and allocating various coefficients to participants with various performances when the parameters are changed, speed up convergence.

Here we design experiments to demonstrate a better performance, converges quickly and capable of heterogeneity data of FL model, we conducted further experiments to replicate three similar research with the different model but same dataset. The results shown in Table 6, indicate that FEDDISTILL [33] optimizes the algorithmic model through a knowledge distillation approach, and directly controls the update of the local model through extract knowledge from the local model to impose an inductive bias. In terms of time-domain optimization, it does not perform well because it fails to account for the slow operation of a single node and the participants' inability to always meet the arithmetic requirements. While the other two proposed FL paradigms FEDBN [10] and FENAVG [9] share the same problem (that is, algorithm recognition accuracy is unstable, and both timeliness and model optimization are difficult to balance).

Table 6. Summary table of model effectiveness and time-domain optimization compared to other studies.

The proposed optimization approach has a smoother performance in recognition accuracy compared with the others, introduce the idea of Bayesian posterior probability to reduce the calculation cost and improve the recognition accuracy of the model. As participants increase, there is no model shift or overfitting problem, and timeliness is improved as well, so it is possible to take into account both the time domain and the algorithmic model. It is clear that the optimization carried out in this study is better than other similar works in the recognition accuracy dimension. One reason is that during the aggregation stage, Pearson correlation coefficients are used to eliminate participants with insufficient data quality, so as to prevent bias in the central model, correctly handles the situation of Non-IID and homogeneous data distribution with different data quality. Introduce the idea of Bayesian Posterior Probability, which reduces the calculation cost, and improves the recognition accuracy of the model. In addition, due to the chain rule, the delay and the loss value of the participant are the focus of our attention in the parameter update phase. When the loss value is low, it proves that the model training is efficient [34] (the two are directly proportional), thus these two parameters are used as the update weight ratio, which can not only accelerate the convergence, but also reduce the delay and improve the accuracy. In general, compared to other federated learning frameworks, the optimized training method proposed in this paper improves accuracy by about 8% and reduces training delay significantly

5.Conclusion

In this paper, we propose a federated learning model with greater advantages in terms of training time consumption and handling heterogeneous data, and apply it to affective computing scenarios, where model construction for sentiment computing, and recognition accuracy are optimized. Variants of FL and related optimization ideas have been proposed continuously. However, there are relatively few studies that can improve both accuracy and timeliness. Federated learning as a distributed computing paradigm can effectively improve the efficiency of model training whereas addressing data security issues. FL is a distributed computing paradigm, which can speed up the learning of models and combine data security. In this study, algorithms based on the theory of greed are used to optimize the steps of federation learning, that is, the selection of participants, the aggregation process, and the updating of parameters. We demonstrate that the proposed method has a good optimization effect, ensuring the effectiveness of the FL training model while reducing training latency. The emphasis on improving the methodological stages is on consuming fewer computer resources, which effectively enhances the efficiency of FL. In the optimization method steps, we focus on reducing the computing resource consumption and thereby increasing federated learning efficiency.

Traditional federated learning performs poorly on non-IID data because of its unified model. The average parameter update rule trains the model, resulting in a different performance for different distributions of data, which loses dynamic information. All participant model parameters are integrated into the central model, resulting in unstable model training [7]. In this paper, we use the Pearson correlation coefficient to exclude models with poor data quality, and experiments have shown that non-IID data perform better. Furthermore, this paper proposes to use the model arithmetic prediction method in FL to estimate how much computation will be required to run the model, as well as to estimate how much power each participant can provide. Select clients with sufficient memory, high-level computing power, and better network bandwidth as participants, which avoids affecting the normal training of the entire federated learning process due to insufficient computing power of a single participant or excessive task load. In the aggregation process, considering the different quality of participants' data, the Pearson correlation coefficient is used to measure the quality of the model, which can promote model optimization and improve training quality. Using the ratio of the estimated delay value and loss value of the participant as the weight coefficient for parameter updating is proposed, which not only takes into account federated learning timeliness, but also optimizes the model's performance. Generally, our research has improved the training quality of federated learning, reduced the training time, and improved its performance.

The paper proposes to optimize the corresponding steps in FL training by effectively combining greedy ideas and algorithms. Using the model arithmetic prediction method to predict the maximum computation required for model operation, and estimating the computation capacity of each participant using the arithmetic formula, then choosing the participant who has fulfilled memory and superior advanced arithmetic, disk memory, and network bandwidth to prevent the issue of insufficient computing resources caused by a single participant, and to avoid situations where the participants themselves are overloaded with tasks that make them unable to work properly. For the aggregation process, inconsistent local training results due to inconsistent participant data quality are considered. And the use of Pearson Correlation Coefficients to measure model quality, rather than using poor quality data, which can lead to model optimization and improved training quality. For the parameter update, it’s proposed using the participants' time delay prediction and loss values as the weight coefficients for updating parameters, which takes into account both the timeliness of FL and the training quality of the model. It successfully increases the level for federated learning training, cuts the training time in half, and improves the effectiveness of the models that are being trained. However, our experiments are still lacking in terms of data security for FL, and the combination of federal learning and affective computing is not comprehensive enough.

When employing the AMIGOS dataset for validation purposes, this study assesses the impact of optimized FL on emotion recognition. The experimental findings indicate that the optimized FL framework surpasses alternative methods for the purpose of affective computing scenarios. The idiosyncrasies of affective computing scenarios are methodically incorporated into each phase of FL training. As a result, in contrast to other approaches, the optimized FL framework leads to a reduction in training time delay by approximately 4 seconds and an increase in model accuracy by an average of 10% when handling non-IID physiological signal data for affective computing.