1. Introduction

Empirical potentials and first principles currently dominate the field of computational materials science. Empirical potentials employ functional analytical equations with explicit coefficients to depict the interactions among atoms and their neighbors. While this method is straightforward and computationally efficient, its accuracy in adhering to physical laws is relatively low. Conversely, first principles, grounded entirely in fundamental physics laws, yield high accuracy but demand substantial computational resources and extended computation times. Both methods are applicable in diverse simulations, each presenting its own advantages and limitations.

Machine learning potentials have gained significant attention in recent years for their ability to overcome the inherent limitations of classical methods like empirical potentials and first-principle computed potentials, including the challenges in potential development and the enormous computational cost. Neural network potentials, developed through the integration of neural network algorithms, are particularly prominent among the various MLPs. Unlike empirical potentials, NNPs' adaptable functional form, extensive fitting target, high accuracy, and portability have established them as one of the mainstream MLPs today.

NNPs can be classified into four generations[1]. This article primarily focuses on the second generation—High Dimensional Neural Network Potentials (HDNNPs), the most renowned and successful among them. As implied by its name, the second-generation NNPs overcome the limitations of their predecessors, which were confined to low-dimensional systems, thus enabling NNPs to solve practical problems more efficiently.

The subsequent sections will first introduce the commonly used computational methods in material science and their respective developmental histories, followed by an emphasis on the practical application areas of high-dimensional neural network potentials.

2. Related theory

This section will offer a succinct overview of the prevalent computational methods currently employed in materials science. Each of these methods possesses its own unique merits and demerits, yet they have all developed over time and are broadly recognized and implemented. These methods are an integral part of this field.

2.1. Empirical Potentials

Empirical potentials offer explicit functional forms, complete with coefficients, that are designed to fit experimental data or results derived from first-principle calculations. Based on the interatomic interactions depicted by the potential function, these can be broadly classified into two-body, three-body, and multi-body potentials. The two-body potential is exemplified by the well-known LJ (Lennard-Jones) potential[2].

Despite its simplicity, the functional form of the LJ potential effectively captures the basic physical properties of numerous atomic systems. Its computational efficiency further contributes to its popularity, making it the most commonly utilized two-body potential.

In real material systems, interactions occur not merely between pairs of atoms but also among multiple atoms coupled together. The three-body potential accounts for both the interactions between atom pairs and the angles between trios of atoms. Examples of typical three-body potentials include the Stillinger-Weber (SW) potential and the Tersoff potential [3, 4].The multi-body potential, which takes into account inter-atomic interactions involving more than three atoms, provides a more comprehensive description of the nature of matter compared to two-body and three-body potentials. The commonly used potentials include the Embedded Atom Method (EAM) potentialand the Modified Embedded Atom Method (MEAM) potential, which is developed based on the EAM potential [5, 6]. The EAM and MEAM potentials, widely used in metal and alloy systems, refer to DFT that uses local electron density to describe the atomic environment.

2.2. Density Functional Theory

Density Functional Theory is a prevalent method in computational materials science, prized for its high accuracy and efficiency. The fundamental concept of DFT is to formulate a generalized function that links total energy with electron density, enabling the replacement of the complex multi-body wave function used in traditional quantum mechanics with the electron density function. This substitution effectively simplifies the multi-body problem in solid systems to a single-body problem.

The initial development of DFT dates back to the 1930s. In 1927, the Thomas-Fermi-Dirac mode was the first to express the kinetic energy of an electron in the form of electron density. In 1928, the Hartree model attempted to use an approximate wavefunction to obtain observables. In 1964, the Hohenberg-Kohn theorem established that individual physical quantities in a stable system could be determined using the density of ground states, a concept that later became known as DFT [7, 8]. In 1965, the inclusion of an exchange-correlation term in the Kohn-Sham equation enabled DFT to address practical problems[8]. However, this required approximate solutions using techniques such as the local-density approximation (LDA) or the generalized-gradient approximation (GGA). In 1980, research by Zunger and Cohen made it possible to calculate the total energy[9].

2.3. Machine Learning Potentials

Machine learning potentials are a set of interatomic interaction potentials derived from machine learning techniques. Contrary to traditional methods, MLPs employ mathematical principles to design a highly flexible functional form and leverage the vast data processing capabilities and robust fitting ability of machine learning techniques to derive a potential function that fulfills the given criteria. The resulting potential function exhibits flexibility, high accuracy, and excellent portability. However, the primary drawback of MLPs is their lack of a physical functional form and the substantial computational resources required for their construction.

The earliest MLPs were Neural Network Potentials proposed by Blank and his colleagues in 1995[10]. For a system with N atoms, NNPs map a 3N-dimensional coordinate space onto a Potential Energy Surface (PES). This mapping relationship is realized through a neural network containing numerous tunable parameters. By optimizing these regression parameters, a smooth potential energy surface can be obtained with minimal error in comparison to the reference energy. Additionally, the energy gradient, or the atomic force obtained by DFT calculations, can be used as a regression target. The vast dataset and high-dimensional parameter space make the parameter optimization process highly complex. However, the robust numerical fitting capability of machine learning methods makes this intricate parameter optimization process feasible.

However, as this method utilizes only a single neural network to depict the PES, the number of input nodes in the neural network increases significantly with the rise in the number of system atoms. Consequently, this method is only suitable for low-dimensional systems.

Over several decades, neural network potentials have evolved to their fourth generation. This discussion will primarily focus on the second-generation NNPs. In 2007, Behler and his team proposed High-Dimensional Neural Network Potentials that define the total energy of a system as the cumulative energy of each atom[11]. By leveraging a distinct neural network for each atom to calculate its energy, HDNNPs effectively addressed the limitation of NNPs being applicable only to low-dimensional systems. A pivotal step in the development of HDNNPs was the introduction of a novel descriptor, the atom-centered symmetric function. This function can accommodate translation, rotation, and atomic substitution invariance. HDNNPs can be bifurcated into two categories according to the type of descriptors: one utilizing descriptors with predefined functional forms, and the other employing descriptors based on auto-learning. The advent of HDNNPs significantly broadens the potential applications of NNPs in real-world material systems.

Besides, MLPs also incorporate kernel-based approaches, including Gaussian Approximation Potentials (GAP), Gradient Domain Machine Learning (GDML), and Spectral Neighbor Analysis Potential (SNAP), among others [12, 13, 14].

3. Application

Currently, HDNNPs have been used in many different material simulation studies, and some representative or pioneering examples will be shown below.

3.1. Ion diffusion

The application of NNPs in simulation studies on amorphous materials presents a promising frontier. The simulation of amorphous materials necessitates large-scale systems. Traditional DFT methods are computationally demanding, a challenge that NNPs can effectively surmount. NNPs have been successfully utilized in conjunction with nudged elastic band, kinetic Monte Carlo, and molecular dynamics methods to characterize Lithium vacancy diffusion behavior in the amorphous Li3PO4 model [15].

NNPs exhibited remarkable efficiency in this context, operating at a speed that is 3 to 4 orders of magnitude faster than DFT. Additionally, the method determined an activation energy of 0.55 eV, a result that aligns excellently with findings from other experimental measurements, thereby verifying its reliability in calculating ion diffusion coefficients.

Figure 1. The diffusivity of Li in amorphous Li₃PO₄ obtained from the large-scale MD using NN potentials. The experimental results were measured with different methods as shown in figure 1[15].

3.2. Nuclear magnetic resonance parameters

A number of solid-state substances can have their local atomic order investigated using the extremely successful experimental method known as nuclear magnetic resonance (NMR) spectroscopy. However, interpreting the corresponding spectra in terms of structural information is rather difficult due to their complexity, especially for amorphous materials. Molecular dynamics simulations, which produce realistic structural models, can be combined with an ab initio evaluation of the quadrupolar coupling tensors and accompanying chemical shift to overcome these issues. However, this method is only applicable to relatively small system sizes due to computational limitations.

Cuny introduces a method for predicting NMR parameters of solid materials utilizing HDNNPs[16]. After training on a collection of representative structures, this method can predict the NMR parameters of an extensive system with remarkable efficiency and accuracy, closely mirroring that of the DFT method. Moreover, it can also be applied to a substantial number of small to mid-sized unit cells, a feat unachievable with DFT-based approaches due to their significant computational power requirements.

3.3. Defect formation

Defects in materials are unavoidable, and they modify the diverse properties of these materials. In the realm of semiconductors, researchers often opt to dope materials to regulate their conductivity. Consequently, it is imperative to investigate the defects in semiconductor materials.

In semiconductors, DFT calculations that employ hybrid functionals are recognized to enhance accuracy. However, this method significantly escalates the computational expense. Conducting dynamical calculations, such as phonons and molecular dynamics on defective systems, typically necessitates substantial configurational space and extended computational durations. These challenges underscore the limitations of DFT calculations in addressing defect properties, even at the level of local density approximation, or GGA.

Koji Shimizu and his colleagues devised a scheme of the NNP to investigate the behavior of point defects in various charge states as we can see in figure 2[17]. They exhibited the performance of the proposed NNP using wurzite GaN, which includes a nitrogen vacancy with 0, 1+, 2+, and 3+ charge states, as a prototype material. Several GaN structures, along with the related total energies and atomic forces obtained from the DFT computations, were used to develop the suggested NNP. The resultant NNP accurately replicated the thermodynamic properties and phonon band structures of defective systems. It is anticipated that the training data preparation process with hybrid functional computations will improve the prediction performance even more. It is expected that the proposed plan will set the foundation for future advancements in ML applications and the growth of materials science research.

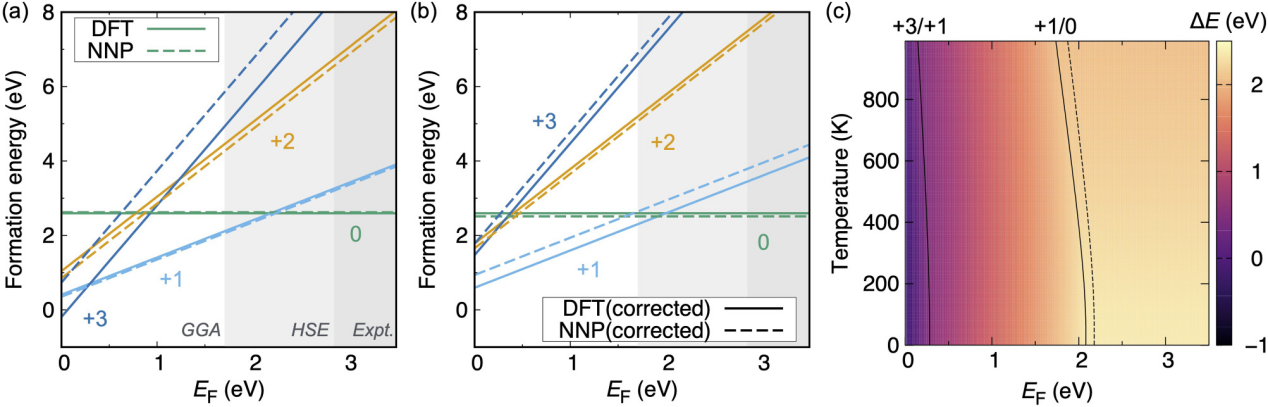
Figure 2. Defect formation energies were calculated as functions of EF (a). The band-gap energies of the experiment (around 3.50 eV), Heyd-Scuseria-Ernzerhof (2.85 eV), and GGA (1.71 eV) are shown by the background colors. (b) Defect formation energies were calculated using the charge adjustments. (c) The temperature dependency of Vq N on transition levels was computed. The DFT (NNP) results are shown as a solid (dotted) line.[17].

3.4. Thermal conductivity

One major hurdle in modern nanoscale electronics is the problem of heat generation in semiconducting materials. The power density and device temperature increase with decreasing device size, which is a major factor in the decline of device performance and dependability. The development of effective techniques for the theoretical simulation of thermal conductivity is crucial for the engineering of semiconductor materials with enhanced thermal management.

One of the most well-established methods for accurate force prediction is DFT calculation, which takes into account the effects of atomic displacement on changes in the electronic state. However, the use of DFT calculations in thermal conductivity models is limited by their high computational cost. The lattice thermal conductivities of semiconductor crystals have been successfully predicted by combining DFT calculations with equilibrium molecular dynamics (EMD) or anharmonic lattice dynamics (ALD) methods. However, because of the exponential increase in computational cost with system size, this technique cannot be applied to systems with more complex structures, such as defective or disordered ones.

Emi Minamitani and Satoshi Watanabe employed HDNNPs in their research on the thermal conductivity of semiconductor materials according to figure 3[18]. For bulk crystals of Si and GaN, the discrepancy from the thermal conductivity computed using DFT is within a 1% range at 200 to 500 K for Si and within a 5.4% range at 200 to 1000 K for GaN. Concurrently, HDNNPs are 800 times more efficient than DFT in calculating thermal conductivity, yet the drawback is the substantial time requirement for preparing the training dataset and tuning the hyperparameters. If the procedure of constructing HDNNPs can be managed within a reasonable timeframe, this could pave the way for a novel and effective approach to studying the thermal performance of complex systems with high precision.

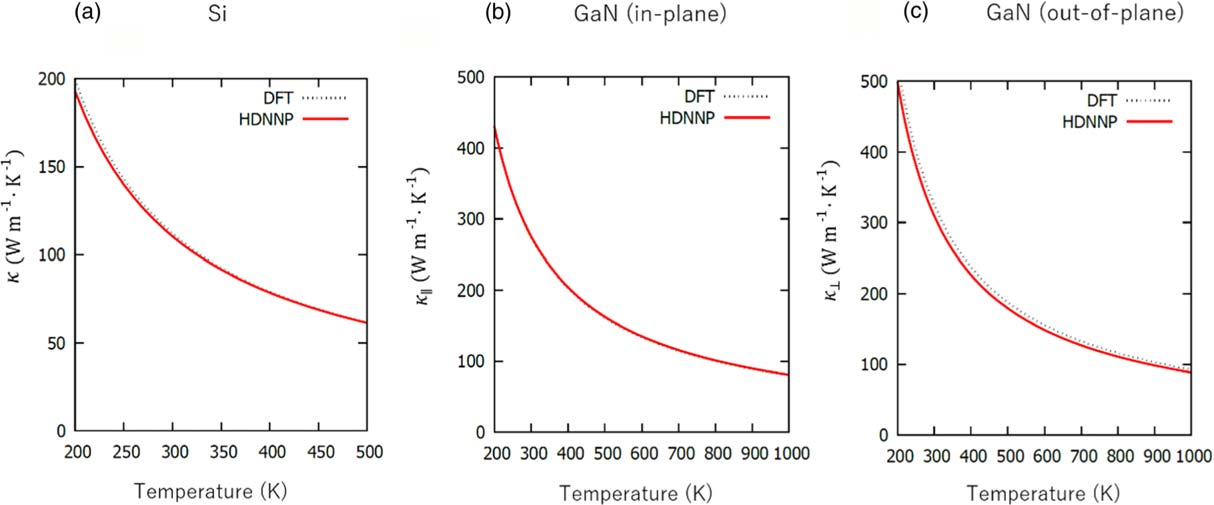
Figure 3. Comparison of thermal conductivities (a) in Si, (b) along the in-plane (100) direction in GaN, and (c) along the out-of-plane (001) direction in GaN obtained by HDNNP and DFT calculations. For the ordinary unit cell in Si and the primitive unit cell in GaN, the supercell sizes used in the computation of the third-order force constant were 2 × 2 × 2. In every instance, an 11 × 11 x 11 mesh was used to sample the Brillouin zone for calculating the linearized Boltzmann equation using the RTA.[18]

4. Challenges and Outlook

Despite the successful application of HDNNPs in various systems, they still present numerous challenges and disadvantages[1].

To guarantee that NNPs can learn all pertinent features of PES, a substantial training data set must be prepared. Considerable time is typically devoted to reference computations to obtain an appropriate training set. In certain systems, this may result in the total computation time using NNPs surpassing that of the DFT approach, rendering NNPs seemingly inefficient.

Owing to their unbiased non-physical functional form, NNPs exhibit limited transferability to configurations that diverge significantly from the training data. Therefore, at present, NNPs are highly accurate only when predicting the energies of atomic configurations that closely resemble the structures in the training set.

The training data for NNPs are derived from DFT reference calculations; thereby, their accuracy is inherently limited by the precision of the DFT method. Even with a highly reliable training method, NNPs cannot assure the correct derivation of desired energies and forces in all instances. Therefore, NNP results should be stringently validated by electronic structure calculations, which also significantly contributes to the time cost.

Another challenge ubiquitous to all contemporary HDNNPs is their incapacity to manage environments with an excessive number of chemical species. This is primarily because as the number of elemental species escalates, the system becomes exceedingly complex, making it challenging to depict the local chemical environment. Notably, this issue is non-existent for low-dimensional molecular PESs.

Undeniably, NNPs present a highly promising approach. However, their progress is currently impeded by the absence of dedicated software designed specifically for NNPs. As NNPs are required to simulate increasingly larger systems, the demand for specialized software escalates[19]. Moving forward, efforts can be directed towards this area to reduce the barriers to using NNPs and enhance the efficiency of researchers' manual tasks.

5. Conclusion

This article scrutinizes the evolution and utilization of high-dimensional neural network potentials. HDNNPs are machine learning potentials that surmount the restrictions of conventional methods like empirical potentials and ab initio calculation potentials, encompassing the challenges of potential evolution and substantial computational costs. HDNNPs have been successfully applied to various large-scale atomic simulations.

Nevertheless, HDNNPs also exhibit certain challenges and deficiencies. Firstly, to ensure that HDNNPs can learn all pertinent potential surface features, an extensive number of training datasets must be prepared, which necessitates a considerable amount of time for reference calculations. Secondly, due to the unbiased non-physical form of the HDNNP function, its transferability is limited when handling configurations significantly different from the training data. Additionally, since the training data for HDNNP is procured from DFT reference calculations, its accuracy is limited by the precision of the DFT method. Lastly, current HDNNPs cannot accommodate environments with an excessive number of chemical species.

Regardless, HDNNP presents a highly promising methodology. Future endeavors can aim towards the creation of software explicitly designed for HDNNPs to mitigate the complexity of utilizing HDNNPs and enhance the efficiency of researchers.