1.Introduction

The A* algorithm is a famous search algorithm used to find the best path from the initial state to the target state in various fields, such as robotics, digital games, DNA alignment, etc. The bidirectional A* algorithm is a heuristic search algorithm improved based on the A* algorithm. Unlike A*, which can only search from the starting point to the end point, it searches from both the initial state and the target state until the boundaries of the two searches meet, thus finding the optimal path. After adopting this strategy, compared with the A* algorithm, the bidirectional A* algorithm can significantly reduce the search space and improve search efficiency [1]. However, because in the conventional bidirectional A* algorithm, the search expansion direction always points towards the fixed end/starting point direction, and the heuristic function does not include obstacles along the way, it cannot avoid dead ends. In situations where this problem exists, the bidirectional A* algorithm usually needs to consume more search space nodes than A* to complete the task [2][3]. Therefore, the first target is improving the heuristic function for better obstacle avoidance capabilities. In view of the fact that in some situations we do not know all the poses of obstacles in advance, there can’t be obstacle parameters added to the heuristic function. Instead, the option of adding the dynamic distance, which represents the distance between the two latest expansion points is taken, so as to make the exploration expansion direction offset towards the other exploration direction. The experiments in this article mainly use Python for algorithm programming and simulation and Matlab for data processing. This research aims to enhance the efficiency of path searching and planning, especially for wheel robots and small autonomous vehicles, in closed two-dimensional rooms like smart factories and hospitals.

2.Literature review

Heuristic algorithm has been famous for long and is a classic algorithm. Within a few years of its invention, many derivative algorithms have been developed, including restricting the search area, decomposing the search problem and limiting the search links [4]. In recent years of research in this field, researchers have mostly made deeper modifications to the original algorithm to better adapt to specific scenarios or some indicators, including adding a large number of parameters to make the algorithm better simulate the real environment [5]; Erke S, Bin D and other researchers carry out more detailed optimization including global planning and key points around obstacles and add new technologies to improve specific indicators [6]; Dexin Yu, Luchen Wang and some other researchers optimize the algorithm to Weighted A* algorithm and the Bidirectional Weighted A* algorithm so that it can still maintain efficiency in a large-scale debt environment [7]. This study focuses on solving the problem of the efficiency of the bidirectional A* algorithm being significantly reduced in certain environments, such as converse and embedded environments. Similar to some of the algorithms studied in other papers, this paper also adds weights to the parameter coefficients of the heuristic function for more subtle adjustments. However, the algorithm in this paper also differs from most algorithms in that it has dynamic parameter and the adaptability, which can adjust the path more flexibly according to the environment. In addition, the algorithm in this paper is also an instant algorithm, which can run smoothly without global information.

3.Background

The A* algorithm first appeared in the 1968 paper "A Formal Basis for the Heuristic Determination of Minimum Cost Paths" by P. E. Hart, N. J. Nilsson, and B. Raphael [8]. The paper elaborates on the basic operation logic of A*: the algorithm uses an open list and a closed list to manage state expansion. The open list stores the search boundary, i.e., candidate states. The closed list stores states that have already been expanded. The A* algorithm selects the state with the smallest f value from the open list for expansion each time, generates its successor states, and adds them to the open list or updates their g values. At the same time, the expanded state is added to the closed list. The algorithm terminates when the open list is empty or the target state is expanded.

By using heuristic information, the A* algorithm significantly reduces the search space without sacrificing the optimality of the solution. The A* algorithm is complete and optimal if the heuristic function is admissible or consistent. The A* algorithm is also the most efficient if the heuristic function is the best, i.e., closest to the actual cost [9].

Due to the potentially exponential number of expanded states, many extensions and variants have been proposed to improve its performance. Some extensions attempt to adapt the A* algorithm for parallel execution, utilizing multi-core machines and computing clusters. Some extensions transform the A* algorithm into a bidirectional heuristic search, i.e., searching from both the initial state and the target state until the boundaries of the two searches meet, finding the optimal path [10].

The basic principle of the bidirectional A* algorithm is to use two evaluation functions, f1 and f2, which combine the actual cost g1 and g2 from the initial state to the current state and the estimated cost h1 and h2 from the current state to the target state, to select the most promising state for expansion. If h1 and h2 satisfy the consistency condition, the bidirectional A* algorithm can guarantee to find the optimal solution.

Unlike the unidirectional A* algorithm, the bidirectional A* algorithm uses two open lists and one closed list to manage state expansion. The open list stores the search boundary, i.e., candidate states. The closed list stores states that have already been expanded by the two searches. The bidirectional A* algorithm selects the state with the smallest f value from the two open lists for expansion each time, generates its successor states, and adds them to the open list or updates their g values. At the same time, the expanded state is added to the closed list. The algorithm terminates when the open list is empty or the boundaries of the two searches meet.

By using heuristic information, the bidirectional A* algorithm reduces the search space and improves search efficiency, as Figure 1 shows. Although it cannot be guaranteed to find the optimal solution, the solution found in practical applications is usually not much worse than the optimal solution.

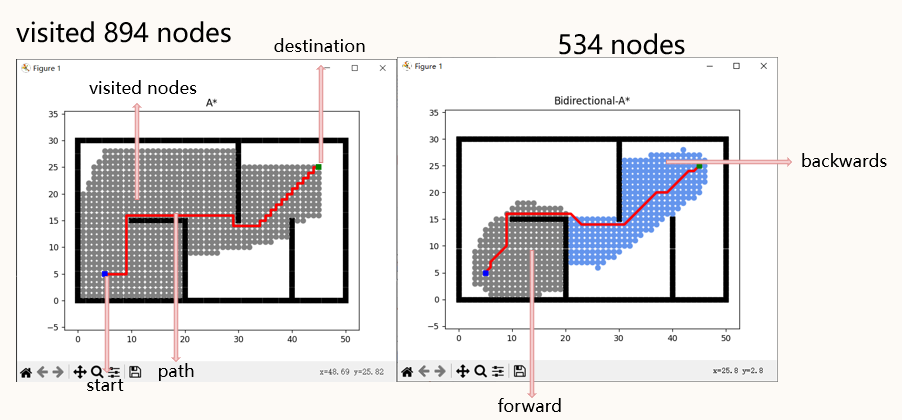
Figure 1. Bidirectional A* better in typical occasion

In response to the shortcomings of the bidirectional A* algorithm, i.e., the search boundaries may miss each other, resulting in a large amount of computation in the post-processing stage, subsequent researchers have proposed many improvements and variants to improve its performance [3]. The algorithm introduced in this article is a bidirectional A* algorithm based on bidirectional dynamic distance.

3.1.Analysis

In typical bidirectional problems, the evaluation function is like as:

\( f = g + h \)(1)

where g represents the actual cost from the start node to the current node, and h estimates the distance from the current node to the target node. Nodes choose to expand neighboring nodes with smaller f values, meaning the search direction always tends to prioritize adjacent nodes closer to the target, without considering obstacles ahead. This includes scenarios where obstacles form detour closed shapes and situations where the graph becomes symmetric about the center after symmetry, like the occasions of Figure 2.

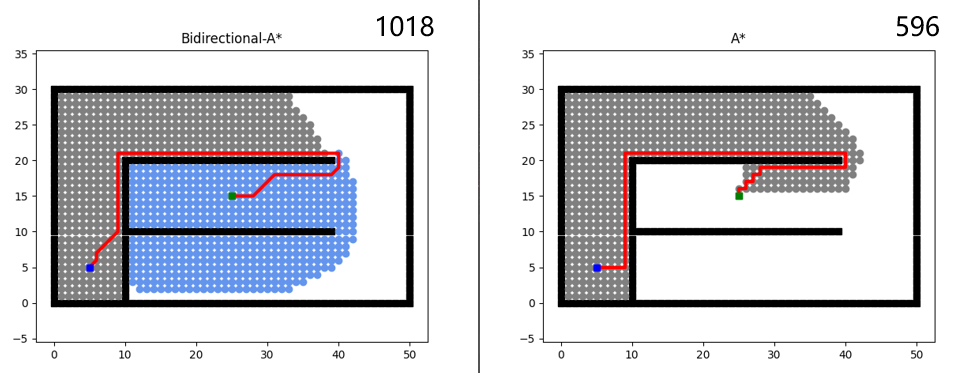
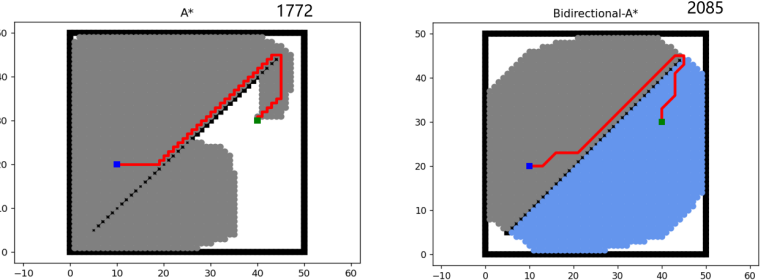
Figure 2. Occasions where bidirectional A* worse than regular A*

In global path planning, since the state of all nodes is known (i.e., the distribution coordinates of all obstacles can be used for path planning), the obstacles can be treated as a higher-weighted component of h. This strategy allows more flexible descriptions of different types of obstacles and terrain effects on the path, making it suitable for global path planning in complex terrains and traffic conditions.

However, if detailed information about obstacle distribution is lacked or it it comes to the second scenario described in the first paragraph, this approach may fail. Therefore, this research needs an algorithm that improves efficiency for both special cases. Considering that the previous conventional heuristic function h had a fixed target point, more dynamic parameters are considered to be incorporated. Since only boundary nodes are constantly changing in the dynamic replacement process between the two lists, the distance between the two boundary nodes is introduced as a parameter into the heuristic function h, creating a dynamic distance. It is assigned a certain weight, resulting in the modified heuristic function:

\( h(n) = distance(static) + a * distance(dynamic) \)(2)

Temporarily setting a = 1, from Figure 3, it is obvious that compared to the conventional bidirectional A* algorithm, this approach significantly improves computational efficiency, reducing node resource consumption by at least 25% or more.

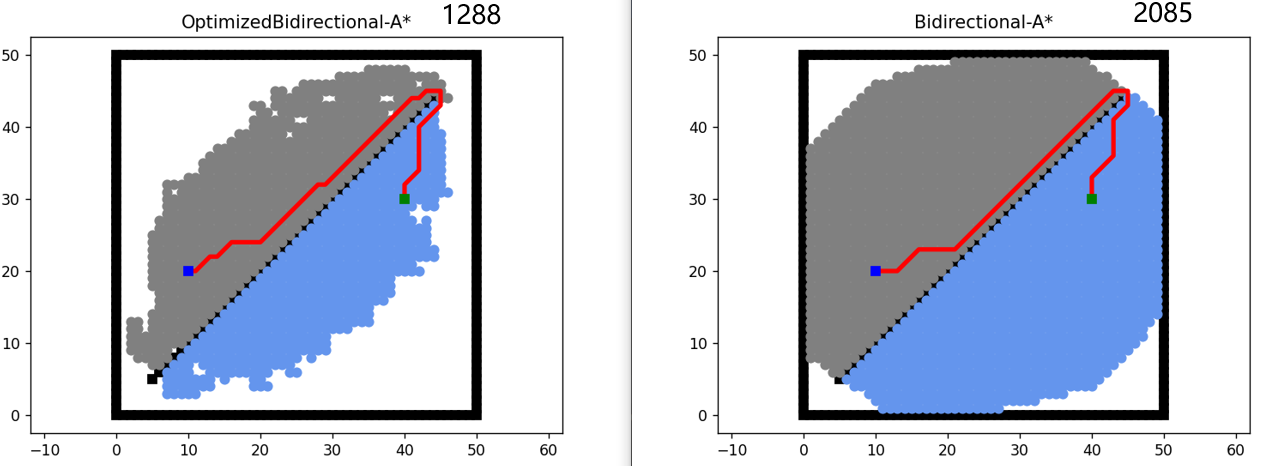
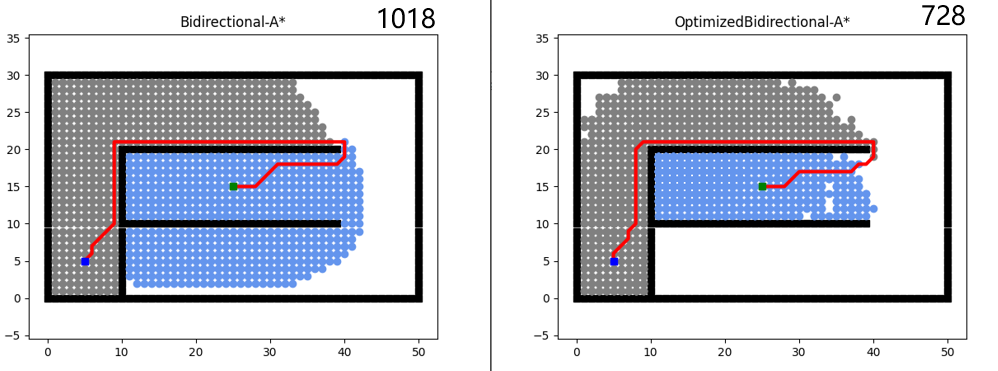
Figure 3. Optimized algorithm improves efficiency

3.2.Experiment

To further explore the impact of the change in weight 'a' on efficiency, the author gradually increases the value of 'a' in four typical situations, then counts the number of nodes consumed and the path length, and obtains the following Figure 4 and Table 1:

Table 1. Results of different environments as 'a' increases

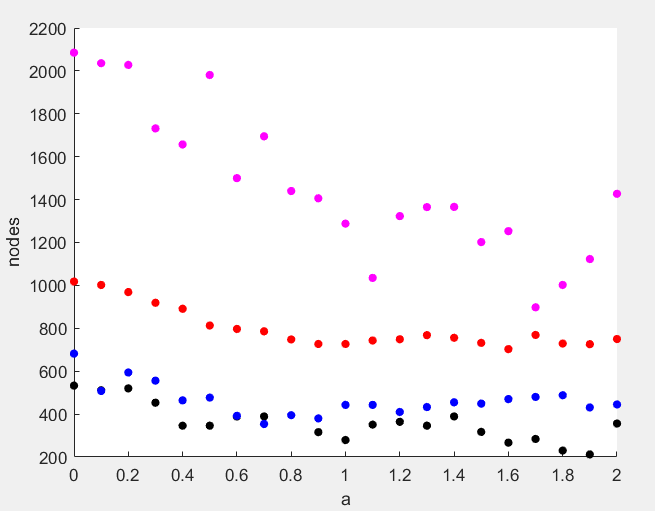
Figure 4. Results of different environments as 'a' increases

From Figure 4, it can be seen that as 'a' increases, the overall trend of the number of nodes is decreasing as all the last values are less than the initial ones, but it is still fluctuating locally. Cases of orange, blue and black where the number of nodes in the conventional bidirectional A* is already small can more clearly show a certain pattern than the larger pink one, and its fluctuations are more similar to the step response curve of the inertia link after reaching the peak, and the amplitude of the fluctuations decreases as 'a' increases. According to the root meaning of the function itself, increasing 'a' will cause the dynamic distance weight to be far higher than the static distance and the cost of the starting point distance, making the two expanded nodes converge at the fastest speed, and the expansion range is almost straight. This can greatly save node resources and improve search efficiency. But at the same time, because the path algorithm is to determine the optimal path according to the evaluation function 'f' after the two parties converge in the searched range, the sharply reduced search range will lead to a reduction in available nodes, and the path finally formed by this is very likely not the shortest path. From Table 1, it can be known that as long as 'a' continues to grow, the probability of the path not being extreme will rise rapidly after reaching a certain level, and looking back at 'a=0', that is, when the algorithm is a conventional bidirectional A* algorithm, all cases can output the best path.

With these data, a general method to achieve the highest efficiency while maintaining the optimal path is summarized as gradually increasing the value of 'a' from 'a=0' until the path obtained several consecutive times is not the optimal path. In the range that has been obtained, the corresponding optimal optimization weight can generally be found. Of course, as the complexity of the problem increases, especially when facing multi-layer problems formed by the combination of multiple simple problems, although the overall trend of node consumption with the growth of 'a' is still gradually decreasing, due to the greatly increased randomness, the local change trend is difficult to predict, and the statistical range needs to be increased to improve the probability of finding the optimal solution.

3.3.Discussion

Because all problem situations show strong specificity and randomness, if a more precise optimal solution is needed, it is basically necessary to calculate all the solutions that meet the conditions within the range one by one, and the burden on computing power will also increase exponentially. Therefore, roughly speaking, this method is not suitable for scenarios that require high-precision optimization, for example, large-scale, complicated circuit planning. This algorithm is more suitable for other scenarios that require a quick response, like vehicle navigation, and because in the above experimental cases, the results of 'a=1' can basically maintain better results compared with the unoptimized bidirectional A* algorithm, there is an average efficiency improvement of 36%, so the author suggests that the weight of 'a=1' can be used in rough scenarios. Of course, in extreme cases, if the application only pursues the speed of the search and does not need the optimal path, a larger value of 'a' can also be used. At this time, the path of the search is almost straight, which is more suitable for quick solving.

4.Conclusion

This paper introduces a new kind of optimized bidirectional A* algorithm to improve efficiency in most situations, including special cases when regular bidirectional A* performs badly. In addition, a principle of further optimization of the weight which can guide to the optimal balance of distance and efficiency is developed. Due to limited conditions, this experiment only changed the weight of the dynamic distance and did not study the weight change of the static distance. Therefore, it is believed that further optimization should be to adjust the weights of both at the same time. They and the path cost 'g' together constitute the entire evaluation function 'f'. Adjusting the weights of the three of them is to change the offset of the expansion direction to the three directions. At the same time, changing the evaluation function 'f' will also change the path selection, which is also a direction of optimization. The heuristic function can be applied in a modular way; just like the adjustment of PID parameters, it should adjust the proportions of various parts according to actual needs to get the optimal solution. Including the dynamic distance mentioned in this article and parameters such as obstacles can be considered as modules to be added, but in the end, it is necessary to balance each item according to computing power and application direction to make the most suitable choice in the end.