Enhancing movie recommendations through comparative analysis of UCB algorithm variants

Qi He

College of Economics, Shenzhen University, Shenzhen, China

2021020054@email.szu.edu.cn

Abstract. In the digital realm, recommendation systems are pivotal in shaping user experiences on online platforms, tailoring content based on user feedback. A notable algorithm in this domain is the multi-armed bandit algorithm, with the Upper Confidence Bound (UCB) emerging as a classic and effective variant. This paper delves into an array of Upper Confidence Bound algorithm variations, encompassing UCB1, Asymptotically Optimal UCB, UCB-V, and UCB1Tuned. The research harnesses the MovieLens dataset to assess the performance of these algorithms, employing cumulative regret as the primary metric. For \( l \) in UCB1 and c in UCB-V, both oversized and undersized parameters will result in negative outcomes. And UCB1Tuned outperforms the other three algorithms in this experiment, since it considers variance and adjusts parameters dynamically. The study demonstrates that setting a appropriate UCB index is crucial for enhancing the performance of the UCB algorithm in recommendation system. It holds significance for both improve recommendation system algorithms and enhance user experience.

Keywords: Reinforcement learning application, Recommendation system, Multi-armed bandits, Upper Confidence Bound (UCB).

1 Introduction

With the evolution of the Internet and communication technologies, recommendation systems have gained significant importance. Confronted with vast information, online platforms increasingly rely on these systems to tailor content to user preferences, thereby optimizing user experience. A key method in machine learning, the multi-armed bandit (MAB) algorithm, has seen extensive application across various domains including recommendation systems, information retrieval, healthcare, and finance [1]. At its core, the MAB algorithm addresses a sequential decision-making challenge under uncertainty, where a decision-maker selects from multiple options over a series of rounds to maximize total reward [2]. Among the various MAB algorithms, the Upper Confidence Bound (UCB) and Thompson Sampling (TS) are notable for their simplicity and proven asymptotic optimality in diverse fields. The UCB algorithm assigns values to each option based on prior data, overestimating the mean reward, and selecting the option with the highest index [3]. The TS algorithm, meanwhile, treats uncertainty probabilistically, continually updating its distribution model to balance exploration and exploitation [4]. The MAB algorithm has spawned several variations, each addressing different aspects of decision-making. The UCB-V algorithm factors in both mean and variance when estimating rewards [5], while the LinUCB algorithm, a contextual bandit variant, leverages user and item features to inform decisions [6]. LinUCB establishes a linear relationship between known rewards and features, aiding in unknown reward estimation. A new iteration, the DivLinUCB algorithm, enhances recommendation diversity by favoring less frequently chosen options [7]. The DeepLinUCB algorithm integrates deep neural networks for non-linear context representation, bolstering both the model's representational power and the performance of recommendation systems [8]. Additionally, the D-UCB algorithm stands out for its near-optimal worst-case regret and lower memory requirements compared to other models [9].

However, there remains a research gap in the comparative study of classic MAB algorithms and their parameters. For instance, Thadikamalla S. and Joshi P. (2023) conducted a comprehensive assessment of four algorithms (Epsilon Greedy, UCB, Softmax, and Thompson Sampling) in adaptive traffic signal management, revealing the superior performance of the Epsilon Greedy algorithm in reducing average travel times and queue lengths [10]. Mambou E N. and Woungang I (2023) explored these algorithms in the context of online advertising, finding that the UCB method garnered the highest average cumulative reward, particularly when specific parameter settings were applied [11].

This study aims to explore various UCB algorithm variants, including UCB1, Asymptotically Optimal UCB, UCB-V, and UCB1Tuned, and to examine the parameter settings in UCB1 and UCB-V. It assesses the performance of different UCB algorithms in movie recommendation systems, seeking to enhance efficiency and effectiveness in online recommendation tasks. The paper is structured as follows: Section II lays the foundational preliminaries; Section III details the experimental setup, including data sources, methodology, and parameter settings; Section IV presents a comparative analysis of the experimental results; and Section V concludes with a summary of findings and directions for future research.

2 Preliminaries

2.1 Multi-armed Bandits

A bandit problem is a sequential game between a learner and an environment [12]. The game is played over n rounds. In each round \( t=1,2,3,……n \) , the learner chooses an action \( A_{t} \) from a set \( A= \) { \( A_{1} \) , \( A_{2} \) , \( A_{3} \) ,……, \( A_{k} \) } of \( k \) possible actions, and then obtains a reward \( X_{t} \) . Actions are often called 'arms' and k-armed bandits means that the number of actions is k.

The learner’s goal is to select actions that maximize the cumulative reward across n rounds, denoted as \( \sum_{t=1}^{n} X_{t} \) . Since the reward \( X_{t} \) is random and its distribution is unclear at first, it’s important to find equilibrium between exploration and exploitation. Exploration refers to receive information about the reward distributions by trying out different arms. Exploitation involves leveraging the acquired information to select the arms that are likely to get higher rewards in the future rounds.

The objective could also be stated as the minimize of regret. Regret is the reward lost by taking sub-optimal decisions. Cumulative regret of an algorithm over n rounds could be defined by:

\( R_{n}=n×μ^{*}-E [\sum_{t=1}^{n} X_{t} \) ] (1)

Where \( n×μ^{*} \) represents the expected cumulative reward of the optimal action \( A^{*} \) , and \( E [\sum_{t=1}^{n} X_{t} \) ] represents the expected cumulative reward of the algorithm.

2.2 UCB

The UCB (Upper Confidence Bound) algorithm is an exploration-exploitation algorithm used to solve the Multi-armed Bandits problem. For every round, UCB algorithm assigns a value called UCB index to each arm, based on the data observed so far that is an overestimate of its mean reward, and then choose the arm with the highest index. The UCB index of each arm updates at every trial and approximates the true expected reward gradually to optimize arms' choice. As more data is collected, the growth rate of regret slows down and the regret curve shows a logarithmic behavior.

2.3 UCB1

UCB1 is a representative algorithm of UCB policies. In round t, the UCB index of arm i is defined as.

\( UCB_{i}(t)=\hat{μ}_{i}(t)+\sqrt[]{\frac{l lnt}{T_{i}(n)}} \) (2)

Where \( \hat{μ}_{i}(t) \) is symbolized as the average reward of arm i from round 1 to round t, n is the total number of rounds, and \( T_{i}(t) \) is the number of selections for arm i. \( l ∈R^{+} \) is a multiplicative factor that affects the UCB index computation, often assigned a value of \( l=2 \) . The second term \( \sqrt[]{\frac{l lnt}{T_{i}(t)}} \) is called exploration bonus.

Each arm should be selected once at the beginning to Initialize UCB index. As show in Table 1, because the UCB index increases as \( T_{i}(n) \) decreases, even if \( \hat{μ}_{i}(t) \) is small, an arm with a small number of samples is more likely to be selected. When there are more samples from arm i, the UCB index will get closer to the true average reward \( μ_{i} \) . Thus, the UCB algorithm could identify the best arm more accurately and be less likely to select a sub-optimal arm.

Aueur proved the upper limit of UCB1 regret: \( Ο(\frac{m ln(n)}{Δ_{min}}) \) , where \( Δ_{min}=\min{a_{i}∈A\{a*}}{μ^{*}-μ_{a_{i}}} \) .

Table 1. Algorithm 1: UCB

2.4 Asymptotically Optimal UCB

Comparing to the UCB1, the UCB index of Asymptotically Optimal UCB is modified as.

\( UCB_{i}(t)=\hat{μ}_{i}(t)+\sqrt[]{\frac{2lnf(t)}{T_{i}(t)}} \) (3)

Where \( f(t)=1+tln^{2}(t) \) .

The regret of Asymptotically Optimal UCB is \( Ο(\frac{2 ln(n)}{Δ_{min}}) \) . It has been proven that the regret ofAsymptotically Optima UCB is smaller than that of UCB1 when \( l=2 \) . The enhancement results from marginally reducing the confidence interval.

Lai and Robbins certificated that there is a matching lower bound on regret for any standard UCB algorithm when n approaches infinity. The upper bound on regret for Asymptotically Optimal UCB matches this lower bound, which means that this algorithm performs better than other algorithm in the limit as n goes to infinity.

2.5 UCB-V

The UCB index of UCB-V is indicated as.

\( UCB_{i}(t)=\bar{X_{i}}+\sqrt[]{\frac{2V_{i}(t)F(t)}{T_{i}(t)}}+ c\frac{3F(t)}{T_{i}(t)} \) (4)

Where \( V_{i}(t) \) is the empirical variance estimate of arm i from round 1 to round t, and could be calculated using equation:

\( V_{i}(s)=(\frac{1}{s}\sum_{γ=1}^{s} X_{i,γ}^{2})-\bar{X}_{i,s}^{2} \) (5)

\( F(t) \) , so-called exploration function, it grows or stays constant as t increases. A common selection for it is \( F(t)= \) \( l \) n(t). c is a positive tunable parameter.

UCB-V algorithm takes variances into consideration. When the sub-optimal arm's variance is significantly smaller than the reward distribution range, using variance estimation allows for a more precise evaluation of the expected rewards. This enables the algorithm to discover the sub-optimal arms faster and minimize the number of selections.

Research has shown that if the exploration function is selected appropriately, the expected regret of the UCB-V algorithm may outperform other algorithms in certain scenarios. The regret of the UCB-V algorithm is concentrated within a certain range and may exhibit a bimodal distribution, with one peak corresponds to a lower regret and the other peak corresponds to a higher regret.

2.6 UCB1-Tuned

The UCB index of UCB1-Tuned is defined in equation:

\( UCB_{i}(t)=\bar{X_{i}}+\sqrt[]{\frac{2ln(t)}{T_{i}(t)}}min\{\frac{1}{4},V_{i}(T_{i}(t))\} \) (6)

Where \( V_{i}(s)=(\frac{1}{s}\sum_{γ=1}^{s} X_{i,γ}^{2})-\bar{X}_{i,s}^{2}+\sqrt[]{\frac{2ln(t)}{s}} \) .

UCB1-Tuned incorporates a new term in the calculation of UCB index that considers the minimum value between the observed variance \( V_{i}(T_{i}(t)) \) and the theoretical upper bound of the Bernoulli distribution variance (i.e., 1/4). This approach ensures that the algorithm considers a conservative estimate of the variance [13]. There is also an addition term \( \sqrt[]{\frac{2ln(t)}{s}} \) in variance calculation. It is a confidence interval width to ensure that the true variance is likely to be within the estimated variance plus this term.

Auer, Cesa-Bianchi, and Fischer inferred that the UCB1-Tuned algorithm typically outperforms the UCB1 algorithm in minimizing cumulative regret.

3 Experimental setup

3.1 Dataset

The experiment is conducted on the MovieLens 1M dataset, which is a stable benchmark dataset of movie recommendation. There are 1,000,209 ratings provided by 6040 users for 3900 movies on the online movie recommendation platform [14]. User IDs, movie IDs, ratings, genres, movie titles, user demographics, and timestamps are all included in each dataset piece. There are 18 unique movie genres. Ratings range from 1 to 5 stars and it can only be integers.

3.2 Methodology

In this experiment, conceptualizing movie genres as "arms" and user ratings as "rewards". There are 18 unique Movie IDs, so the number of arms is 18. A five-star rating system is used, so the reward in each round could be 1 to 5. Before running the algorithm, calculate the average rating of movies in each genre as the actual average rating for that genre. Cumulative regret is chosen as the evaluation metric. The cumulative regret is defined as: \( R_{n}=n×μ^{*}- \sum_{t=1}^{n} X_{t} \) ,where \( μ^{*} \) is the largest average rating among movie genres, and the corresponding movie genre is the actual optimal arm. \( \sum_{t=1}^{n} X_{t} \) is the actual cumulative reward obtained by running the algorithm. The number of rounds in each experiment is set as n=20000. This research sets up 30 experiments in total, with data being shuffled in each experiment. Finally calculate the average regret of 30 experiments.

The research in this paper will cover the following aspects:

For UCB1 algorithm, varying the multiplicative factor \( l \) to investigate its impact on algorithm performance. And evaluating how well the UCB1 performs with varying numbers of arms when \( l \) is set to 2.

For UCB-V algorithm, setting distinct values of tunable parameter c to compare the performance of the algorithm. The exploration function \( F(t) \) is defined as \( l \) n(t) in this experiment.

Comparing the performance of four algorithms: UCB1, Asymptotically Optimal UCB, UCB-V, and UCB-1Tuned. For the Asymptotically Optimal UCB, setting \( f(t)=1+tln^{2}(t) \) .

4 Results and analysis

Experimental results are shown in Figure 1 to 7.

Figure 1. presents the performance comparison of different \( l \) values for the UCB1 algorithm. It shows that if \( l \) is too large or too small, the average cumulative regret will be high. The cumulative regret curves show logarithmic behavior when \( l \) ≥ 0.5, which indicates that the growth rate slows down over time and gradually converging towards the optimal choice. While the curves present linear behavior when \( l \) < 0.5, which means that the algorithm still selects the sub-optimal arms many times.

Referring to Figure 2. and Figure 3., the error bars are relatively small when \( l \) ≥ 2. This illustrates that the algorithm performs stably in several experiments. However, the error bars are quite large when \( l \) < 2, and it increases with the decrease of \( l \) . This demonstrates that the algorithm is unstable. It may perform well in one experiment, but it could also be poor.

Overall, the value of \( l \) could not be too large or too small. In this experiment, the UCB1 algorithm performs the best when \( l \) = 2, since it is stable and has the lowest average cumulative regret.

Figure 4. shows the performance comparison of various k(arms). It could be observed that with the decrease of k, the average cumulative regret decreases. Generally, the algorithm would be easier and faster to find the optimal arm when k is smaller.

From Figure 5. and Figure 6., they evident that the impact of c on the UCBV algorithm is similar to that of \( l \) on the UCB1 algorithm. The value of c should be chosen neither too large nor too small to maintain a trade-off between exploration and exploitation, so as to reduce cumulative regret and volatility. Among the parameters c tested in this experiment, the UCB-V algorithm outperform others when c is set to 1.

Figure 7. presents the average cumulative regrets and error bars of four algorithms: UCB1, UCB, Asymptotically Optimal UCB, UCB-V, UCB1Tuned. In this experiment, UCB-V c=2 shows the highest cumulative return, while Asymptotically Optimal UCB is in third place. UCB1 \( l=2 \) and UCB1Tuned are in the second and first positions.

Figure 1. Average Cumulative Regrets Comparison for UCB1 with Different \( l \) Values (Photo/Picture credit: Original).

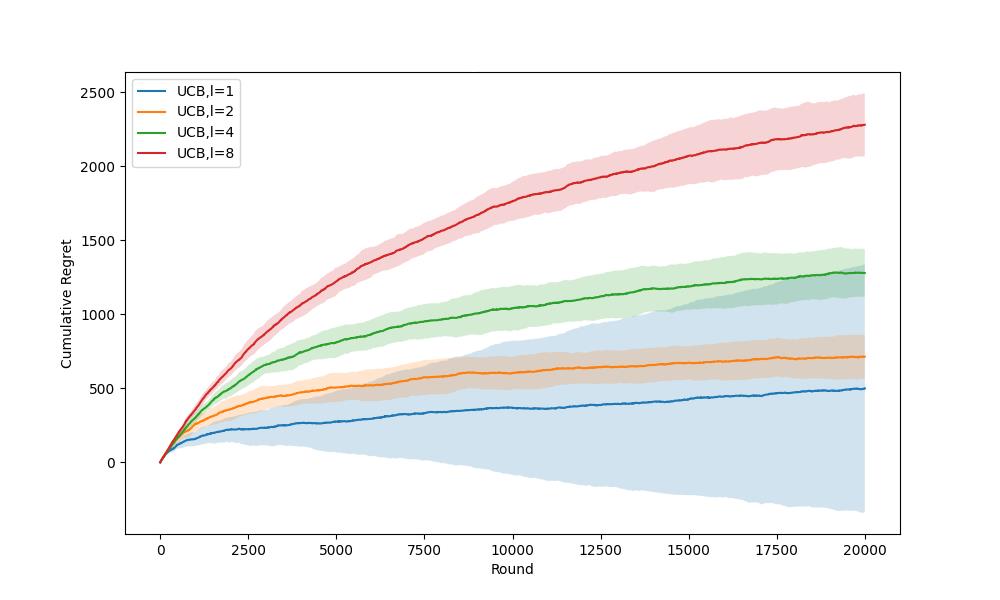
Figure 2. Error Bars Comparison for UCB1 when \( l \) = [ 1, 2, 4, 8] (Photo/Picture credit: Original).

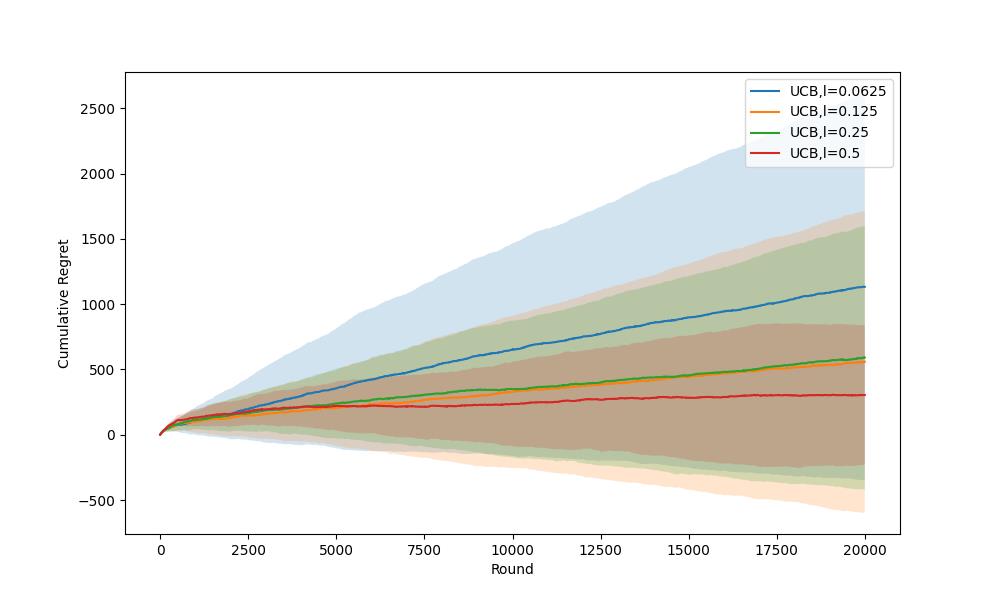
Figure 3. Error Bars Comparison for UCB1 when \( l \) = [0.0625, 0.125, 0.25, 0.5] (Photo/Picture credit: Original).

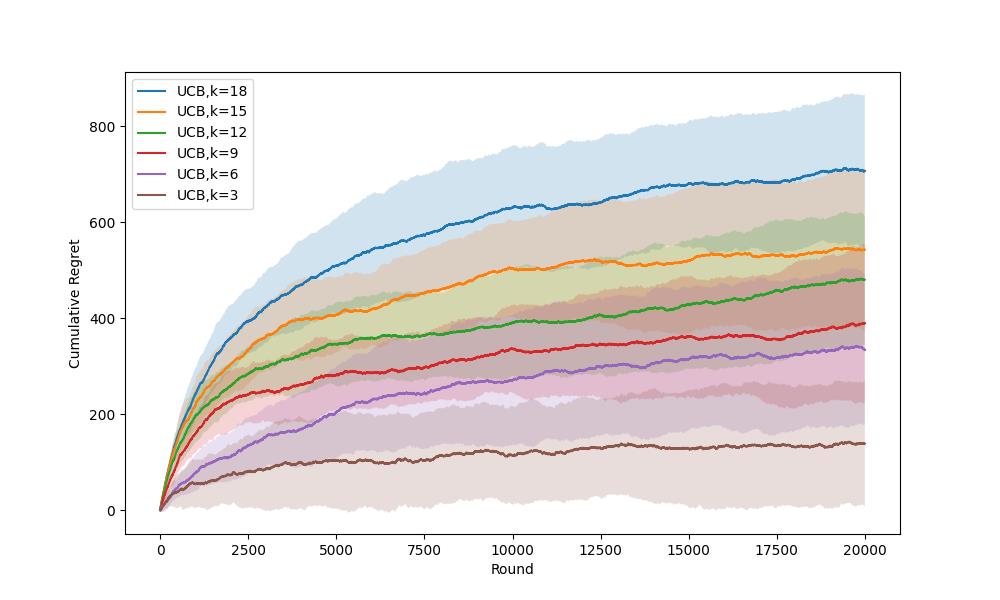
Figure 4. Average Cumulative Regrets Comparison for UCB1 with Different k (arms) (Photo/Picture credit: Original).

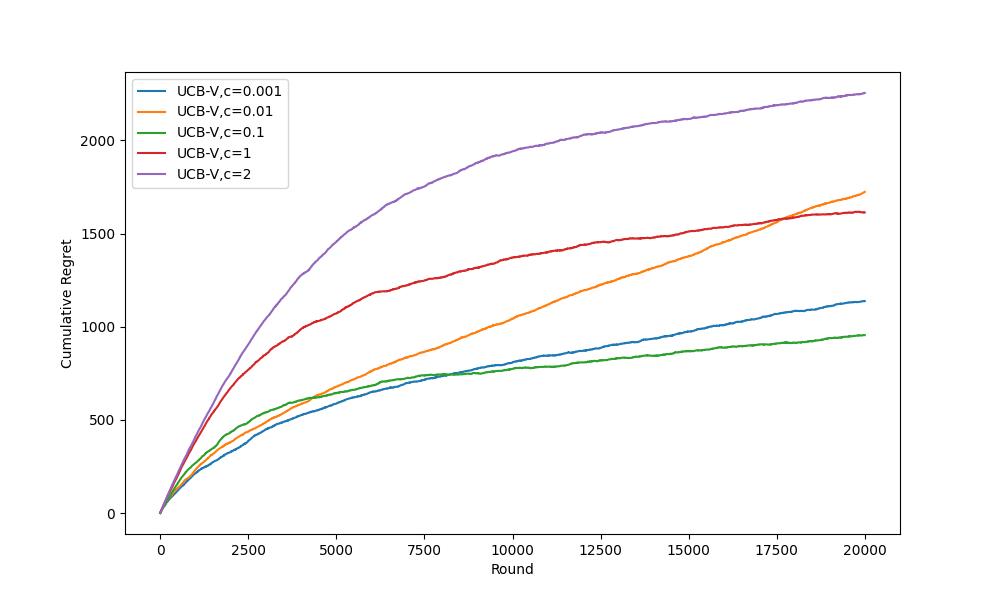
Figure 5. Average Cumulative Regrets Comparison for UCB-V with Different \( l \) Values (Photo/Picture credit: Original).

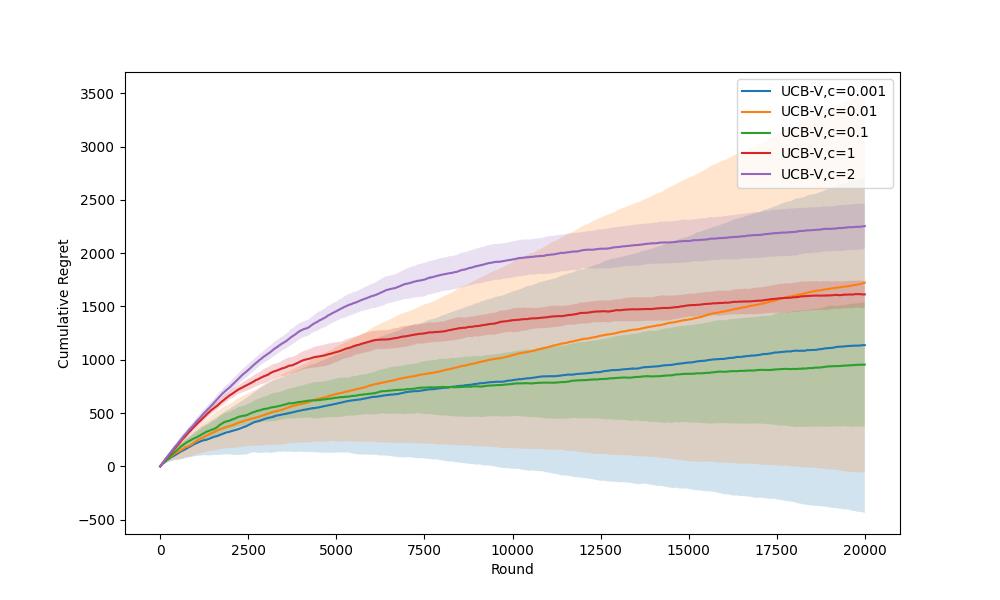
Figure 6. Error Bars Comparison for UCB-V with Different \( l \) Values (Photo/Picture credit: Original).

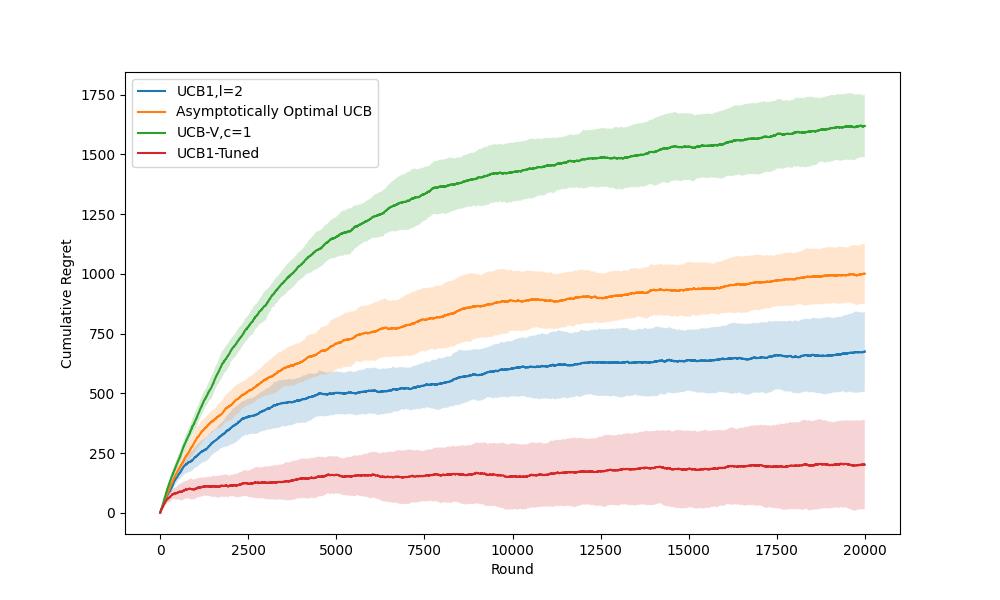
Figure 7. Comparison of UCB and its variants algorithms (Photo/Picture credit: Original).

5 Conclusion

This study presents a comparative analysis of various variants of the Upper Confidence Bound algorithm within the context of movie recommendation systems. It focuses on the impact of specific parameters, particularly ℓ in UCB1 and c in UCB-V, on algorithmic performance. A key finding is that these parameters considerably influence effectiveness: higher parameter values lead to greater exploration due to an increased exploration bonus, potentially causing inefficient reward utilization during the extensive search for the optimal arm. Conversely, lower parameter values prompt more aggressive exploitation, risking repeated selection of sub-optimal arms and resulting in lower rewards. The experiments demonstrate that UCB1-Tuned outshines other variants in minimizing cumulative regret. This superior performance stems from its incorporation of variance and dynamic adjustment of the exploration factor for precise arm selection. However, the UCB-V algorithm demands careful calibration of the tunable parameter c, as it directly affects performance. These insights underscore the significance of optimizing algorithm parameters to enhance performance in recommendation systems. Given the large user base these systems cater to, managing reward variance is crucial for improving user experience; thus, the exploration bonus should not be set too narrowly. The study acknowledges its limitations, notably the exclusion of contextual bandit algorithms and the diversity of recommended content. Future research could investigate alternative UCB algorithm variations and examine the impact of parameter settings on performance. Such advancements will contribute to the ongoing refinement of recommendation algorithms, ultimately enriching user experiences.