1. Introduction

With the emergence and popularity of concepts like the metaverse, virtual reality, and augmented reality, real-time graphics rendering technology has attracted increasing attention. Apart from graphical quality, frame rate – the number of frames rendered per second during real-time rendering – is a crucial comparison metric [1]. In computer graphics applications aimed at real-time rendering of graphical images, mathematical computations account for a significant portion of the overall processing time. Among these, linear algebra, specifically matrix and vector operations, plays a foundational role by enabling the precise representation of points' positions and transformation processes in multidimensional space [2]. Thus, to deliver a more real-time and seamless user experience, enhancing the efficiency of mathematical computations in the graphics rendering process has become a paramount concern for professionals in the field.

This study will focus on how to enhance the performance of matrix operations during graphics rendering. By constructing practical rendering scenarios, we will compare the performance of two popular scientific computing libraries to identify the reasons behind performance discrepancies and explore the potential of combining their strengths to achieve superior performance. In practical graphics rendering, a model's position needs to be determined through multiple matrix transformations. During this process, the efficiency of different mathematical libraries may vary, affecting the time taken to render images and consequently influencing real-time rendering frame rates [3]. Therefore, by comparing frame rates when rendering a substantial number of models, we can assess the rendering performance when using different mathematical libraries. By optimizing the computational efficiency of this process, we can significantly reduce the generation time for a single frame, resulting in a smoother visual experience. In various applications of real-time graphics rendering, such as games, 3D simulations, and metaverse scenarios, higher frame rates typically equate to a more realistic experience and reduced discomfort.

This paper is divided into five main sections. Section two will review prior literature on topics like spatial transformation operations. Section three will primarily focus on detailed comparisons and presentation of specific data results. Section four will analyze the reasons behind performance disparities by combining real-world data and characteristics of mathematical libraries. Lastly, section five will summarize the paper, discuss its limitations, and outline potential future research directions.

2. Literature review

2.1. Computer Graphics

Computer graphics is a branch of computer science that explores the creation and manipulation of visual content, particularly in computer-driven simulations and animations. The applications of computer graphics are extensive, encompassing areas such as film and television special effects, video games, computer-aided design (CAD), virtual reality, web graphics, and many other domains. The evolution of computer graphics traces back to the 1960s. Initially, it found use primarily in military and research contexts, such as flight simulators and molecular modeling. Over time, computer graphics expanded its applications to more diverse fields, including art and entertainment.

In the work of Bonneel and Digne [4], they extensively delve into optimal transport theory and its applications in computer graphics and computer vision. Optimal transport theory is a mathematical tool that facilitates comparison and transformation of different probability distributions. Within computer graphics, this tool proves useful in addressing various problems, such as image processing, geometry manipulation, rendering, fluid simulation, computational optics, and more. Another perspective on computer graphics is presented in the review by Riddle [5], which examines Gaboury's book. This work explores the materiality of computer graphics, traces the history of rendering images, and discusses their impact on contemporary computing. An article by Díaz-Barrancas et al. [6] introduces the use of hyperspectral textures in virtual reality systems to enhance real-time computer graphics applications. Their scientific contribution lies in improving the authenticity of color representation, especially concerning scene lighting conditions and their precision. Lastly, Wang [7] explores the utilization of self-supervised learning to distinguish computer-generated images from natural images. This approach harnesses a wealth of unlabeled data and employs a training process capable of generating labels, obviating the need for manual labeling.

2.2. Optimization of Virtual Engines

As personal computers and computer graphics rendering technology have become widespread, the performance of hardware specialized in image rendering operations (e.g., GPUs) has garnered increasing attention. In the work of Owens et al. [8], the development of GPU performance is discussed from the perspective of general-purpose GPU computing. The article elaborates on the advantages of GPUs compared to other computational hardware (e.g., CPUs). It highlights that the multi-core parallel nature of GPUs, contrasting the linear operation of CPUs, grants GPUs superior capabilities for handling graphics rendering tasks. Given that the process of matrix operations can also be decomposed into multiple independent subtasks, the notion of optimizing matrix operation performance through parallelism naturally emerges. Efforts and studies by Kelefouras et al. [9], RSTAD et al. [10], and Jiang and Snir [11] have validated this idea. Their accomplishments have been widely adopted in contemporary computer graphics rendering.

3. Research methods

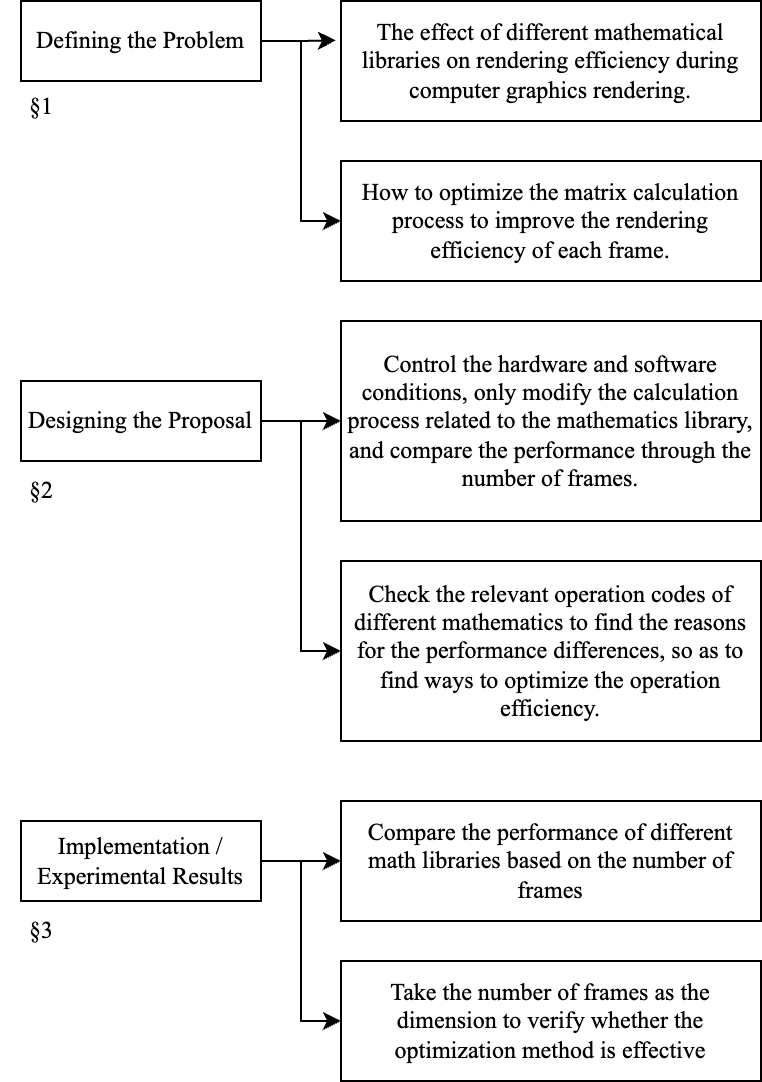
3.1. Overall Research Structure/Flowchart

Figure 1. Overall Research Flowchart.

In this study, we undertake explorations and optimization efforts concerning the efficiency of calculations within the computer graphics rendering process. Throughout this process, we design experimental environments, conduct experiments with relevant parameters, arrive at final comparative results, and validate optimization strategies through these outcomes.

3.2. Existing Techniques

3.2.1. OpenGL

OpenGL (Open Graphics Library) is a cross-language, cross-platform application programming interface used for rendering 2D and 3D vector graphics. It typically interacts with GPUs to achieve hardware-accelerated graphics rendering. The first version of the OpenGL specification was released by Silicon Graphics, Inc. in 1992. Since then, OpenGL has found extensive applications in fields including CAD, virtual reality, scientific visualization, and electronic gaming. Starting from 2006, the non-profit industry consortium Khronos Group took over control of the OpenGL specification [12].

3.2.2. GLM

GLM (OpenGL Mathematics) is a Header-Only Library designed to serve graphics software development based on OpenGL. Developed following the OpenGL Shading Language (GLSL) standard, GLM boasts excellent compatibility not only with GLSL and OpenGL but also for developers familiar with both [13].

3.2.3. Eigen3

Eigen3 is a C++ template library developed for linear algebra purposes. It encompasses various optimizations targeting multiple use cases and scenarios from a computer hardware perspective, including SIMD (Single Instruction, Multiple Data) and Expression Template Metaprogramming, resulting in outstanding computational efficiency [14].

3.3. Optimization Approaches

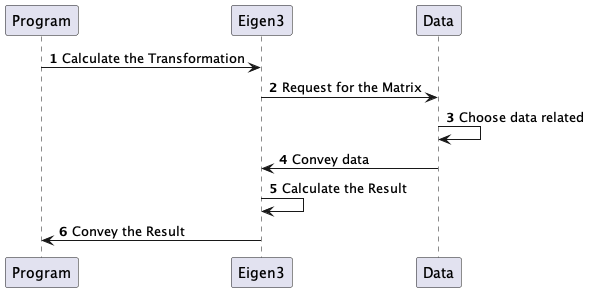
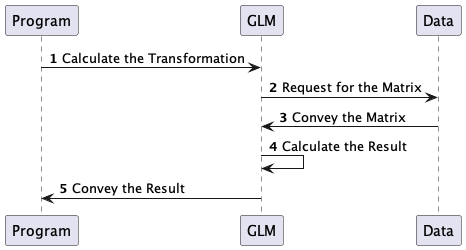
Figure 2. Comparison of Eigen3 and GLM Computation Processes.

In Eigen3, data structures like Transform are specifically provided for storing and performing geometric transformation operations. These structures aim to ensure logical clarity during design and efficiency during high-scale complex operations of storing, retrieving, and modifying transformation values. However, during the actual process of rendering graphical images on a computer, the scale of single transformations isn't substantial, and the matrix dimensions are not large (four-dimensional matrices). Consequently, optimizations intended for higher dimensions and larger-scale computations might become inefficient due to repeated encapsulation and multiple invocations. Thus, a possibility exists that, compared to Eigen3's provided Transform structures, using matrices for naive three-dimensional transformations might yield greater efficiency.

In GLM, both data storage and computation methods are straightforward, involving direct storage and calculations. Conversely, Eigen3 incorporates technologies like Expression Template and Metaprogramming, optimizing the library's efficiency from both computational process and computer architecture perspectives. Consequently, a possibility exists that, compared to GLM's naive implementation approach, Eigen3's computation and storage structures might offer superior efficiency.

In summary, a possibility exists that, by combining GLM's spatial transformation computation with Eigen3's foundational computation and storage structure implementation, maximum graphics rendering efficiency can be achieved.

3.4. Experimental Setup

In addition to using the same software and hardware conditions, the experiments in this study were conducted within a constructed test scenario. This scenario comprises 20,000 rock models rapidly orbiting a single planet model.

3.5. Evaluation Criteria

In this study, we utilize the average frame generation rate as a quantitative measure for evaluation.

The frame generation rate refers to the number of frames that a program can render within a unit of time, expressed in FPS (Frames Per Second). Due to potential time discrepancies when different mathematical libraries calculate the same content, resulting in varied time consumption for rendering a single frame, the accumulated effect over time reflects specific discrepancies through the frame generation rate (higher frame generation rate indicating better performance).

The average frame generation rate refers to the program's average frame generation rate within a unit of time, preventing occasional fluctuations in frame generation rates from affecting the results.

4. Experimental results

Under the previously mentioned conditions, the results from running the three code implementations are as follows:

Figure 3. Screenshots of the Test Scenario Used in this Experiment.

From the experimental results, it is evident that the program utilizing rewritten transformation functions exhibits an improvement of approximately 1 FPS in terms of frame rate, compared to the programs using Eigen3's built-in transformation functions and those employing GLM's built-in transformation functions.

Another noteworthy observation is that the program utilizing Eigen3's built-in transformation functions displays a lower frame rate by approximately 0.3 FPS compared to the program using GLM's built-in transformation functions.

This discrepancy becomes more pronounced when the CMAKE_BUILD_TYPE is switched to Debug mode:

Data from Table 3 reveals that in Debug mode, the performance gap between Eigen3 and GLM is further magnified, with a frame rate difference of around 10 FPS.

5. Discussion

Based on the data from the experimental results, we can draw preliminary conclusions: The optimization approach proposed in this study, which involves reducing nested function calls for small-scale transformation operations and directly performing calculations, proves effective. Additionally, through comparisons, it is evident that the repetitive calling of multiple functions in Eigen3 does indeed impact performance when compiler optimization is not applied. However, post-compiler optimization, the performance difference caused by this factor becomes negligible. Therefore, it can be inferred that with the ongoing advancements in compiler technology, the performance impact of nested function calls in Eigen3 is likely to diminish. The comparison between the "Using Eigen3 with Transformation Functions Rewritten according to the Proposed Optimization Approach" group and the "Using GLM with its Built-in Transformation Functions" group also illustrates that with the same transformation function implementation, Eigen3's data structures and computational performance are superior. Consequently, in the foreseeable future, when compiler-induced performance overhead due to repeated function calls is eliminated, Eigen3's overall performance is expected to surpass that of GLM.

From the experimental data, it is evident that the test scenario constructed for this experiment remains relatively simplistic. Increasing the number of rock models reveals that the performance bottleneck primarily stems from rasterization processing rather than transformation computations. This phenomenon could be attributed to the hardware's limitations used in the experiment or to the possibility that the OpenGL API employed in this experiment lags behind more cutting-edge APIs such as DirectX12, Metal, and Vulkan.

6. Conclusion

In today's context, with the continuous maturation of computer graphics, rapid advancements in consumer computers, and graphics rendering-related hardware, both users and content creators are increasingly attentive to the performance of graphic image rendering, particularly in the realm of three-dimensional spatial image rendering. As attention shifts towards rasterization performance, it is equally essential not to overlook the transformation process that occurs prior to rasterization. To investigate the performance and optimization methods within this aspect, this study compared the frame rates of rendering programs using two computational libraries: GLM and Eigen3. By contrasting the implementation approaches between the two libraries, we explored the factors causing performance disparities and proposed an optimization approach. Based on the experimental results, we can conclude that, under the premise of using built-in transformation functions, GLM's performance slightly surpasses that of Eigen3. However, after rewriting the transformation functions with the proposed optimization approach, Eigen3's performance outperforms GLM's. This study has solely attempted an optimization approach involving reducing multi-layered function calls. Beyond this, there are optimization avenues to explore, such as those based on Cache utilization and parallel computation. These avenues remain open for further in-depth exploration in subsequent research.