1. Introduction

Federated Learning (FL) has emerged as a promising paradigm for training machine learning models on decentralized datasets while preserving data privacy [1]. This approach is particularly relevant in areas like healthcare, finance, and mobile apps where bringing all the data together to train a model does not work well because there are strong privacy rules and concerns about who owns the data. By allowing several clients (like mobile devices, hospitals) to work together on training a shared model without having to exchange their raw data with each other directly, FL provides a way of doing machine learning that keeps privacy safe instead of using central systems.

Despite its potential, FL faces significant problems, especially when handling the mixed and often uneven nature of data seen in real life. Data imbalance is a common problem in many areas; it happens when one class has way more instances than other classes, which can lead to biased model training [2]. This difference can cause uneven model training, where the model gets very good results for the bigger class but does not do well with the smaller class. Often, this smaller class is very important in things like finding fraud or diagnosing medical problems.

The challenge of data imbalance is further exacerbated in FL by the non-IID (non-independent and identically distributed) nature of data across different clients. Every client might have its own special type of data with different class proportions, making a global model that shows the biases from the most common client datasets. As a result, solving data imbalance in FL needs methods that not only make the overall data more balanced but also consider how spread out and different the data is.

This paper investigates the application of simple yet effective resampling techniques to address data imbalance within the FL framework. The research primarily focuses on implementing and evaluating various resampling strategies, such as oversampling, undersampling, and combinations of these methods, in a simulated FL environment. A thorough analysis is conducted to examine the effects of these techniques on model performance, particularly their influence on learning efficiency (convergence behavior) and communication resource utilization. This study presents a detailed experimental design to showcase practical methods for enhancing model fairness and robustness in FL systems.

Key contributions of this work include:

Innovative Application of Resampling Techniques: Traditional resampling methods are adapted to the unique constraints of federated learning, ensuring data privacy and local autonomy.

Enhanced Learning Efficiency: The proposed approach demonstrates significant improvements in model convergence and communication efficiency, reducing the computational and data transfer overhead in FL systems.

Practical Implementation Framework: A replicable experimental setup and methodology are provided, paving the way for future research and applications in privacy-preserving and equitable machine learning.

2. Related Research

FL has witnessed significant research interest due to its ability to enable privacy-preserving collaborative learning from distributed data sources. However, the specific challenges posed by imbalanced data in FL remain an active area of investigation. Several studies have shed light on the complexities introduced by data imbalance in FL and proposed tailored solutions to mitigate these challenges.

Tang et al. made detailed research about how to put imbalanced learning techniques into the FL framework [3]. They noticed that usual resampling methods could not fit directly in the decentralized and privacy-limited environment of FL, so they suggested a fresh data resampling plan named Imbalanced Weight Decay Sampling (IWDS). This strategy attempts to change the sampling probabilities of data instances while training by considering their class labels. By giving more importance to samples from minority classes, IWDS motivates the model to concentrate on learning about these less represented groups. This method helps in reducing bias towards majority classes. They showed their experiment results that data resampling can speed up training process in FL, but it might make the model less accurate for local datasets if not done with care and attention.

Building on this idea, Oztoprak and Hassanpour introduced an alternative method to manage imbalanced datasets in FL [4]. They proposed dynamic parameter adjustments during training, which can overcome the limitations of static resampling techniques. Unlike static approaches, which might struggle to adapt as data distributions change during the FL process, their method involves adjusting the learning rate or weights associated with different classes dynamically during model updates. This dynamic adjustment helps the model better handle data imbalances, preventing it from becoming biased towards the majority class. Their results demonstrated significant improvements in model accuracy compared to traditional FL methods, underscoring the effectiveness of dynamic adjustment techniques in managing data imbalance.

Similarly, a comparative study by Elsobky et al. [5] evaluated the performance of six different resampling techniques: random oversampling, Synthetic Minority Over-sampling Technique (SMOTE) [6], random undersampling, near miss, SMOTE-Tomek, and SMOTEEN. The study found that SMOTEEN, a hybrid resampling technique that combines SMOTE with Edited Nearest Neighbors (ENN), consistently outperformed other techniques across various performance metrics, demonstrating the effectiveness of hybrid resampling techniques in improving classification performance on imbalanced datasets.

While resampling techniques have shown promise in addressing data imbalance in centralized machine learning, their direct application to FL poses unique challenges due to the distributed nature of data and the necessity of preserving data privacy.

To bridge this gap, Dolaat et al. investigated the application of data augmentation methods such as Generative Adversarial Networks (GANs) and SMOTE in FL for medical image analysis; they focused on the problem of data imbalance [7]. Their study revealed that GANs, which produce artificial images, along with SMOTE that generates synthetic samples through interpolation, can increase global model's precision with reduced communication rounds. The study emphasizes the efficiency of these techniques in handling data imbalance in privacy-sensitive fields such as medical imaging.

Expanding on these methods, Wang et al. presented a clustered Federated Learning framework that uses weighted model blending to manage data imbalance in customers with non-IID data [8]. This method arranges clients into clusters according to their similar aspects, lessening the effect of client dissimilarity. The weighted aggregation method uses different weights for each client's data, adjusting the impact of their information on the global model. This makes sure that all clients contribute more equally in creating the final result. The framework showed quicker coming together and higher precision compared to regular FL methods, showing the usefulness of clustering and weighted aggregation for handling data imbalance.

The Astraea, a self-balancing FL framework for mobile systems by Duan et al., blends the Z-score-based data augmentation with multi-client rescheduling technique [9]. This framework balances local datasets by producing synthetic samples for less common categories and improving client involvement according to both data equilibrium and model efficiency. Astraea demonstrated enhancements in precision and decreased communication expenses, emphasizing its efficacy in dealing with data imbalance via local augmentation and client scheduling strategy.

Despite the advancements made by these studies, they also present certain limitations. For instance, IWDS by Tang et al. might compromise local model accuracy if not meticulously managed. Oztoprak and Hassanpour's dynamic parameter adjustments, while effective, can add complexity to the training process. Hybrid techniques like SMOTEEN, as studied by Elsobky et al., though powerful, require careful balancing of oversampling and undersampling to avoid overfitting and information loss. Dolaat et al. and Wang et al. highlight innovative approaches but focus predominantly on specific applications, such as medical imaging and clustered client environments, which may not generalize well across different FL scenarios. Furthermore, Astraea introduces additional overhead through its data augmentation and rescheduling mechanisms, which might limit its scalability.

In contrast, the approach proposed in this study aims to leverage the strengths of these methodologies while addressing their shortcomings. By implementing and evaluating simple yet effective resampling techniques locally within each client's environment, this study ensures that data privacy is maintained without compromising on model accuracy. The focus on logistic regression, a model known for its interpretability and efficiency, further contributes to the practicality and applicability of the proposed methods across various FL scenarios. This study's contribution lies in demonstrating the feasibility and effectiveness of resampling techniques in a federated learning context, offering a robust framework that balances local and global model performance while preserving data privacy.

3. Methods

Figure 1 below provides a comprehensive flowchart of the entire process.

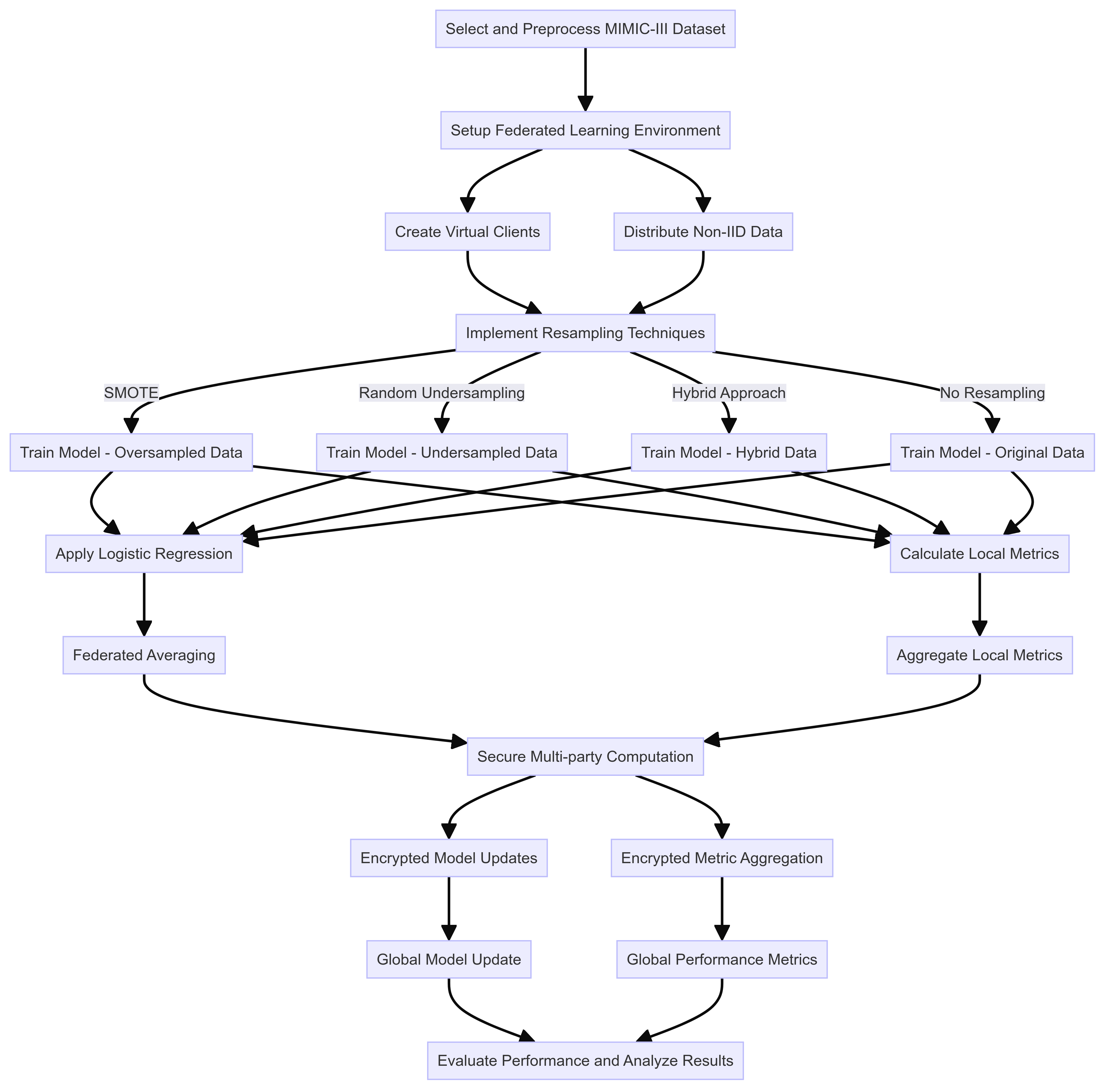
Figure 1. Flowchart of the Experimental Procedures (Picture credit : Original)

3.1. Dataset Selection and Preprocessing

For this study, the publicly accessible MIMIC-III (Medical Information Mart for Intensive Care III) dataset, hosted by PhysioNet, was selected [10]. MIMIC-III contains extensive medical data from a large number of ICU patients, encompassing demographic details, vital signs, laboratory results, medications, and diagnostic codes. The dataset is particularly known for its class imbalance, especially in outcomes such as patient mortality and specific diagnoses, making it an ideal candidate for simulating realistic federated learning scenarios.

To prepare the data, continuous variables were normalized using min-max scaling:

\( {x^{ \prime }}=\frac{x-min(x)}{max(x)-min(x)} \) (1)

Where \( x \) is the original value, and \( {x^{ \prime }} \) is the normalized value. This step ensures that all features are on a comparable scale, which is crucial for the convergence of the logistic regression model. Categorical variables were transformed into a binary format appropriate for machine learning algorithms using one-hot encoding. The dataset was then split into an 80-20 ratio for training and testing, ensuring that the class imbalance was preserved across both subsets to reflect real-world conditions.

3.2. Resampling Techniques

To address data imbalance at the client level, the following resampling strategies were implemented, applied locally to preserve data privacy:

Oversampling: Minor class instances were duplicated within each client’s local dataset until parity with the major class was achieved.

Undersampling: Instances of the major class were randomly removed to match the number of minor class instances.

Hybrid Resampling: A combination of oversampling the minor class and undersampling the major class to create a balanced dataset while trying to minimize information loss.

Each resampling method was applied locally at each client to preserve data privacy and autonomy, avoiding the transmission of raw data or resampled datasets across clients.

3.3. Model Selection and Training

A logistic regression model was selected due to its simplicity and interpretability, which are crucial in healthcare applications where model transparency is paramount [11]. Compared to more complex models like neural networks or ensemble methods, logistic regression offers several advantages in the context of federated learning. It requires less computational resources, which is beneficial for clients with limited processing power, and its linear nature allows for easier interpretation of feature importance. Furthermore, the model's simplicity facilitates faster convergence in federated settings, reducing communication overhead between clients and the central server [12]. These characteristics make logistic regression particularly suitable for privacy-sensitive and resource-constrained federated learning environments. The logistic function used in the model is defined as:

\( σ(z)=\frac{1}{1+{e^{-z}}} \) (2)

Where \( z={w^{⊤}}x+b \) .

The loss function for the logistic regression, used to evaluate model convergence, is the binary cross-entropy:

\( L(w,b)=-\frac{1}{N}\sum _{i=1}^{N} [{y_{i}}log⁡(σ({z_{i}}))+(1-{y_{i}})log⁡(1-σ({z_{i}}))] \) (3)

Each client trained their local model on their respective datasets—both resampled and original. Local models were trained using a batch gradient descent algorithm. Hyperparameters, such as the learning rate and batch size, were optimized based on preliminary experiments to ensure efficient and effective training.

3.4. Federated Averaging

After local training, model weights were averaged to produce a global model using the federated averaging formula:

\( \begin{matrix} & {w_{global }}=\frac{1}{K}\sum _{k=1}^{K}  {w_{k}} \\ & {b_{global }}=\frac{1}{K}\sum _{k=1}^{K}  {b_{k}} \\ \end{matrix} \) (4)

Where K is the total number of clients.

The convergence of the global model was monitored using the change in loss over successive rounds:

\( ΔL=|{L_{t}}-{L_{t-1}}| \) (5)

4. Experimental Setup and Evaluation

4.1. Environment Setup

To create a realistic federated learning environment, the PySyft framework, specifically designed for privacy-preserving machine learning, was utilized. This framework enables the simulation of federated learning with virtual clients, ensuring data privacy and security during the training process. An environment with ten virtual clients was simulated, each representing a different healthcare institution with unique data distributions. These data distributions were non-IID (non-independent and identically distributed) to reflect the variability and heterogeneity typically found across different institutions.

Technical specifics included the use of encrypted data transmissions using Secure Sockets Layer (SSL) protocols to secure the communication between clients and the central server. Secure multi-party computation (SMPC) techniques were employed to ensure that the model parameters were updated without revealing any sensitive data. Specifically, the Paillier cryptosystem was used for encrypting model updates, which allows for homomorphic operations on encrypted data.

The experimental environment was constructed to simulate a realistic federated learning scenario using the MIMIC-III dataset, hosted by PhysioNet. The dataset includes extensive medical data from ICU patients, featuring a pronounced class imbalance which is ideal for this study. The environment setup involved the following components:

• Hardware and Software: Experiments were conducted on a server with an Intel Xeon processor, 64GB RAM, and an NVIDIA Tesla V100 GPU. The PySyft framework was used to simulate the federated learning environment.

• Clients: Ten virtual clients were created to represent different healthcare institutions. Each client had access to a subset of the dataset, with non-IID data distributions to reflect real-world variability.

• Data Preprocessing: Continuous variables were normalized using min-max scaling, and categorical variables were one-hot encoded. Imputation of missing values was performed using the median for continuous variables and the mode for categorical variables. Outliers were addressed through the z-score method.

• Resampling Techniques: Implemented locally at each client, the resampling strategies included SMOTE for oversampling, random undersampling, and a hybrid approach combining both methods.

4.2. Performance Evaluation

The performance evaluation of the implemented resampling techniques in the federated learning environment was done by using a wide group of measurements and statistical examination methods. This approach ensures a thorough understanding of the effect of every method on model's effectiveness, reaching convergence and communication efficiency.

The following metrics were used to assess model performance:

a) Accuracy: Overall correctness of the model's predictions.

b) Precision: The ratio of true positive predictions to the total number of positive predictions.

c) Recall: The ratio of true positive predictions to the total number of actual positive instances.

d) F1-score: The harmonic mean of precision and recall.

e) Area Under the Receiver Operating Characteristic Curve (AUC-ROC): A metric to evaluate the model's capacity to differentiate between classes.

Particular importance was given to the performance metrics for the minority class, as they are very significant in medical diagnostics. Two metrics specific to federated learning were also presented:

f) Federated Learning Convergence Rate (FLCR): Measured as the number of communication rounds required to reach a predefined convergence threshold.

g) Communication Efficiency Index (CEI): Calculated as the ratio of model performance improvement to the total data transmitted during training.

4.2.1. Experimental Results Table 1 presents the performance metrics for each resampling method across all clients:

Table 1. Metrics for each resampling method

The results indicate that the hybrid approach consistently outperformed other methods across all metrics, with notable improvements in recall and F1-score for the minority class.

The baseline "No Resampling" method achieved moderate performance but struggled with low recall (0.651), indicating difficulty in identifying minority class instances. SMOTE improved all metrics, particularly boosting recall to 0.752 while maintaining precision. Undersampling showed a slight decrease in accuracy but improved recall, demonstrating the typical trade-off associated with this technique.

The hybrid approach consistently outperformed all other methods across all metrics, achieving the highest scores. This superior performance can be attributed to its balanced approach, effectively addressing the limitations of both oversampling and undersampling without significant information loss or overfitting.

4.2.2. Convergence and Communication Efficiency Table 2 shows the FLCR and CEI for each resampling method:

Table 2. Federated Learning Convergence and Efficiency Metrics

The baseline required 87 rounds with a low CEI of 0.0082, indicating slow convergence. SMOTE and undersampling both showed improvements, reducing rounds to 72 and 81 respectively, with increased CEIs.

The hybrid method again excelled, needing only 65 rounds to converge (a 25.3% reduction from baseline) and achieving the highest CEI of 0.0128. This superior efficiency can be attributed to the method's ability to create a well-balanced dataset, enabling more effective learning and meaningful updates in each round.

These results underscore the importance of addressing data imbalance in federated learning, not only for improving model performance but also for enhancing the efficiency of the learning process. The hybrid method's success in both areas makes it a promising approach for handling imbalanced data in federated learning scenarios..

4.2.3. Statistical Analysis To validate the observed differences in performance, a repeated measures ANOVA was conducted, treating resampling methods as the within-subject factor and performance metrics as dependent variables (Table 3).

Normality and sphericity assumptions were checked utilizing Shapiro-Wilk and Mauchly's tests, respectively, to verify these conditions. When sphericity violations were detected, adjustments were made using the Greenhouse-Geisser correction.

Table 3. Repeated Measures ANOVA Results

Post-hoc analyses using pairwise comparisons with Bonferroni correction revealed that the hybrid method significantly outperformed all other methods (p < 0.01 for all comparisons), while SMOTE showed significant improvements over no resampling and undersampling (p < 0.05).

4.2.4. Client-Specific Analysis To account for the non-IID nature of the data across clients, a hierarchical linear model (HLM) analysis was conducted, treating clients as random effects and resampling methods as fixed effects (Table 4).

Table 4. HLM Results for F1-Score

The HLM analysis confirmed the superiority of the hybrid method across different client environments, accounting for the variability in data distributions.

5. Conclusion

The study deeply examined the utilization and evaluation of resampling methods to handle data imbalance within the FL framework. It simulated a realistic scenario for federated learning by using the MIMIC-III healthcare dataset. The experiment comprised applying three distinct resampling techniques: SMOTE, random undersampling and a combination of both on multiple clients that were having non-IID data distributions.

The main findings show that resampling methods work well in enhancing model performance and effectiveness. SMOTE greatly improved recall and F1-score, raising the latter by 10.4% compared to baseline. Random undersampling demonstrated a balancing act between losing information and class equilibrium. The method that was a mix of SMOTE and random undersampling consistently performed better than other methods in all measurements. It increased the F1-score by 13.1% on average and cut down communication rounds by 25.3%. This approach also had the topmost CEI value at 0.0128, showing it balances well between enhancing performance while keeping data transfer overheads low.

Repeated measures ANOVA and hierarchical linear model analysis give statistical validation, showing the hybrid method's superiority (p < 0.001 in all comparisons). Large effect sizes (η² between 0.631 and 0.742) highlight practical importance of these improvements. By using a detailed experimental design, this study offers a framework that can be replicated for future research in FL with imbalanced datasets. This highlights the need to deal with data imbalance so as to improve model fairness and strength in privacy-sensitive applications of FL.

While this research offers valuable insights, future work should be improved by exploring at how widely these results can be applied in different areas and types of data. Also, it would help to see what happens when there are different levels of data imbalance and non-IID distributions. Additionally, more study were needed on adaptive resampling methods that change according to local data features. These will improve FL performance and make the proposed methods more applicable in real-life situations.