1. Introduction

The application of multi-armed bandit algorithm in dynamic pricing has become a hot topic in academia and industry in recent years. With the development of internet technology and big data analysis capabilities, dynamic pricing strategies have been widely applied in various fields, from high-speed train tickets to fresh products, from airline tickets to automobile inspection services. As an effective online learning method, the multi-armed bandit algorithm has shown great potential in handling dynamic pricing problems. This paper will provide a review of recent related studies and discuss the rationality and application prospects of the multi-armed bandit algorithm in dynamic pricing.

Firstly, the multi-armed bandit algorithm has shown excellent performance in dealing with demand uncertainty. In their study on dynamic pricing of high-speed train tickets, Bi Wenjie and Chen Gong built a multi-stage decision-making model and designed a DQN framework based on deep reinforcement learning, while the demand function was unknown [1]. Their study showed that this method could accurately capture demand information and make flexible adjustments to decision-making in different states, resulting in a 4.58% higher revenue than the optimal fixed price strategy in a random demand environment. Similarly, Zhang Yifan used a method based on the multi-armed bandit (MAB) model when studying dynamic pricing of niche products [2]. He proposed an algorithm based on UCB improvement and another based on a Bayesian framework, which performed well in simulation environments and had some robustness to the distribution changes and random risk of real data. These studies show that the multi-armed bandit algorithm can effectively handle the uncertainty and dynamic changes in demand, providing more precise pricing strategies for enterprises.

Secondly, the multi-armed bandit algorithm has shown its advantages in handling high-dimensional, complex dynamic pricing problems. Bi Wenjie and Zhou Yubing modeled the fresh product joint inventory control and dynamic pricing problem as a Markov decision process and designed an algorithm based on deep reinforcement learning [3]. Their method effectively solves the dimensionality disaster problem and is more adaptable to the complex and variable real environment, with stronger adaptability and generality. This method takes into account the randomness of product shelf life, time-varying state transition functions, and the influence of inventory status on customer retention price, making the model more in line with reality. Similarly, Fang Chao and others adopted an online learning method when studying the dynamic selection strategy of new product development project portfolios, and learned the project revenue information in real time through Bayesian updating [4]. Their research shows that the dynamic model performs better than the static model in highly uncertain environments.

Moreover, the multi-armed bandit algorithm also exhibits unique advantages in handling strategic consumer behavior. Bi Wenjie and Chen Meifang proposed a non-parametric Bayesian algorithm that combines Gaussian process regression and Thompson sampling to study the dynamic pricing problem faced by retailers simultaneously facing demand uncertainty and strategic consumers [5]. Their research found that, contrary to common belief, retailers' revenue is higher when strategic consumers exist, and it increases as consumers' patience increases. This may be because retailers explore optimal prices more extensively in the presence of strategic consumers. This finding provides a new perspective for understanding consumer behavior and formulating dynamic pricing strategies.

However, the application of the multi-armed bandit algorithm in dynamic pricing also faces some challenges. For example, Tang Jue et al. showed that consumer loyalty has a significant impact on pricing strategies [6]. For short-sighted consumers, the equilibrium pricing of the seller is influenced by both the transaction time and consumer loyalty; while for strategic consumers, the equilibrium pricing of the seller is not affected by the transaction time, but is affected by the transaction period and consumer loyalty. This complex dynamic relationship may increase the difficulty of the multi-armed bandit algorithm. Similarly, Zhang Chen and Tian Qiong studied that in the online pricing of airline tickets, factors such as passenger loyalty level and the number of competitors would affect the airline's channel selection and pricing strategy. The complexity of these factors may pose challenges to the multi-armed bandit algorithm [7].

Moreover, the multi-armed bandit algorithm faces challenges in handling dynamic pricing problems under limited resource constraints. Ma Shuangfeng and Guo Wei studied the rate control and dynamic pricing problem in a serial queue system under limited resource constraints [8]. Their study shows that the optimal price is not always increased as the number of customers in the queue increases. When the waiting cost of customers is high and the number of customers at a certain service counter is large, the price needs to be lowered first to attract customers, and then gradually increased. This complex dynamic relationship may require a more complex multi-armed bandit algorithm to handle.

Another noteworthy issue is the impact of consumer time preference and product quality information update on dynamic pricing. Xu Minghui et al. showed that consumer perceived quality and strategic cost affect their purchase strategy and lead companies to implement different dynamic pricing strategies [9]. More interestingly, they found that the improvement of review information accuracy is not always beneficial to companies. When both the consumer's strategic cost and perceived quality are high, even more accurate review information can cause both a decline in the firm's profits and a reduction in consumer surplus. This complex dynamic relationship places higher demands on the multi-armed bandit algorithm.

The reference price effect is another important factor to consider in dynamic pricing. Feng Zibai modeled the random evolution of reference prices using a stochastic differential equation and modeled the dynamic pricing problem as a random optimal control problem at an infinite time horizon [10]. His research showed that when consumers receive new price information faster, the expected stable state reference price may increase; when the reference price effect is stronger, the variance of the stable state reference price may decrease. This complex dynamic relationship may require more complex multi-armed bandit algorithms to handle.

Finally, Cui Zibin's research reminds us that in a competitive environment, the impact of consumer learning on the firm's pricing strategy is complex [11]. For example, when the proportion of socially learning consumers increases, competing firms should reduce product differentiation, but revenue will increase. This complex competitive dynamic may require more complex multi-armed bandit algorithms to handle.

Despite these challenges, the application prospects of the multi-armed bandit algorithm in dynamic pricing are still broad. Liu Xu's demand-based dynamic pricing algorithm for perishable goods, which utilizes the potential of the multi-armed bandit algorithm, demonstrates that the algorithm can estimate the demand function by optimizing the optimal price and price range in each learning stage, resulting in a smaller difference between the actual maximum yield obtained through learning and the theoretical value under different price sensitivity levels [12]. More importantly, the algorithm performs better in large-scale scenarios, proving the necessity of fully demand-based learning for perishable goods.

In summary, the application of the multi-armed bandit algorithm in dynamic pricing shows great potential. It can effectively handle the uncertainty and dynamic changes in demand, adapt to the complex and changing real environment, and handle strategic consumer behavior. However, it also faces challenges such as handling consumer loyalty, limited resource constraints, consumer time preferences, reference price effects, and competitive environments. Future research should focus on solving these challenges to further improve the applicability and effectiveness of the multi-armed bandit algorithm in dynamic pricing. At the same time, combining the multi-armed bandit algorithm with advanced technologies such as deep learning and reinforcement learning may lead to more innovative solutions. In summary, the multi-armed slot machine algorithm's application in dynamic pricing is reasonable and has broad development prospects.

2. Research Design

This study aims to evaluate the performance of multi-armed bandit (MAB) algorithms, specifically the adaptive upper confidence bound (asUCB) and Thompson Sampling (TS), in crop pricing strategies. The focus is on assessing whether these algorithms can effectively fit historical real data and demonstrate robust pricing strategies in simulations.

2.1. Algorithm Selection and Model Design

This study employs two classic MAB algorithms: asUCB and TS. The asUCB algorithm adapts to decision-making challenges in uncertain environments by dynamically adjusting confidence intervals, particularly excelling in handling significant price fluctuations. This method can real-time balance the ratio between exploration and exploitation to pursue optimal pricing strategies. The TS algorithm is a probabilistic distribution model established on Bayesian inference principles, designed to determine the best pricing strategy by analyzing sample data. It excels at optimizing the decision-making process through continuous learning iterations, demonstrating its capability to progressively converge to the optimal solution in the face of uncertainty. Below are the specific implementation details for each algorithm:

During the model construction process, a simulated agricultural product market scenario was created. In this scenario, retailers adopted the asUCB and TS strategies, dynamically adjusting purchase prices to maximize profits from past data, and used a simulated environment to verify the actual efficacy of their pricing mechanisms. The dataset was systematically divided into a training subset and a simulation subset, with the former supporting the learning and adaptation process of the algorithms, and the latter assessing the generalization ability of the algorithms on new data.

2.1.1. Implementation of the UCB Algorithm

def UCB_algorithm(num_rounds, number_of_arms, B=4):

cumulative_regret = np.zeros(num_rounds)

arm_counts = np.zeros(number_of_arms)

arm_rewards = np.zeros(number_of_arms)

for t in range(number_of_arms):

reward = calculate_reward(t)

arm_rewards[t] += reward

arm_counts[t] += 1

cumulative_regret[t] = regret(t, t)

for t in range(number_of_arms, num_rounds):

ucb_values = arm_rewards / arm_counts + B * np.sqrt(np.log(num_rounds) / arm_counts)

arm = np.argmax(ucb_values)

reward = calculate_reward(arm)

arm_rewards[arm] += reward

arm_counts[arm] += 1

cumulative_regret[t] = regret(t, arm) + cumulative_regret[t - 1]

return cumulative_regret

During the operation of the UCB algorithm, at each time step, the confidence intervals (ucb_values) of each arm are reassessed, and the arm with the highest confidence interval value is selected. By continuously accumulating the rewards received and the frequency of selections for each arm, the algorithm dynamically harmonizes the relationship between exploring new opportunities and exploiting known advantages, achieving an efficient balance between the two.

2.1.2. Implementation of the TS Algorithm

def TS_algorithm(num_rounds, number_of_arms, B=4):

cumulative_regret = np.zeros(num_rounds)

arm_counts = np.ones(number_of_arms)

arm_rewards = np.zeros(number_of_arms)

for t in range(number_of_arms):

reward = calculate_reward(t)

arm_rewards[t] += reward

cumulative_regret[t] = regret(t, t)

for t in range(number_of_arms, num_rounds):

theta = np.random.normal(arm_rewards / arm_counts, B / (2 * np.sqrt(arm_counts)))

arm = np.argmax(theta)

reward = calculate_reward(arm)

arm_rewards[arm] += reward

arm_counts[arm] += 1

cumulative_regret[t] = regret(t, arm) + cumulative_regret[t - 1]

return cumulative_regret

In the operational mechanism of the TS algorithm, at each time step, a normally distributed value \(\theta\) is generated for each arm, and the arm with the highest \(\theta\) value is selected for action. This algorithm progressively optimizes the decision-making process by continuously updating the reward feedback and selection frequency of each arm, gradually converging to the optimal solution.

2.2. Experimental Setup

The data splitting method is as follows: We use the early part of the actual historical data to construct the training set, aiming to provide learning material for the asUCB and TS algorithms so they can master past price trends and derive the best bidding strategies; the later part of the historical data is used as the simulation set to assess the effectiveness of the bidding strategies established during the training phase in future market conditions.

2.3. Data Processing and Generation Method

By extracting and processing historical crop price records, we divided the dataset into training and simulation testing parts, aiming to ensure that the model not only fits within a theoretical framework but also validates effectively in a simulated market environment. The algorithm iteratively tunes the pricing strategies to achieve optimal model fitting and tests the effectiveness of these strategies in the simulation scenario.

2.4. Model Validation and Evaluation

During the training phase, the optimal choices (i.e., the best product or price) of each algorithm are identified through the accumulated feedback. Specifically, the asUCB algorithm adopts the criterion of maximizing confidence intervals to determine the optimal option; the TS algorithm, on the other hand, selects the optimal arm based on maximizing the success rate.

best_arm_ucb = np.argmax(ucb.values)

best_arm_ts=np.argmax(thompson_sampling.successes/(thompson_sampling.successes+thompson_sampling.failures))

We apply the optimal strategy identified during the training phase to the simulated dataset to predict the performance of the price variable \(z\) in this simulated scenario.

test_predictions_ucb = test_data['product'].apply(lambda x: optimal_rewards_dict[best_product_ucb] if x == best_product_ucb else 0)

test_predictions_ts = test_data['product'].apply(lambda x: optimal_rewards_dict[best_product_ts] if x == best_product_ts else 0)

2.5. Selection of Evaluation Criteria

When assessing model performance, we adopt Mean Squared Error (MSE) as the core evaluation parameter to judge its adaptability on the test dataset. MSE quantifies by calculating the mean squared deviation between the model's predicted values and actual conditions. The smaller the deviation, the higher the model's fitting accuracy.

mse_ucb = mean_squared_error(test_data['price'], test_predictions_ucb)

mse_ts = mean_squared_error(test_data['price'], test_predictions_ts)

mse_ucb, mse_ts

In the process of evaluating performance, we compared the performances of the asUCB and TS algorithms on the Mean Squared Error (MSE) metric, aiming to explore their relative superiority in fitting historical data and predicting future prices.

2.6. Tools and Implementation

This experiment is conducted using Python, utilizing libraries such as Pandas, NumPy, Matplotlib, and Scikit-learn for data processing tasks, algorithm implementation, and graphical presentation of results. The experimental environment is configured with an Intel i9 processor and 16GB RAM, ensuring efficient computation and high precision of results.

3. Result analysis

3.1. Training Set Performance

Within the training dataset, both the asUCB algorithm and Thompson Sampling (TS) identified optimal pricing strategies. We determined the best-performing strategy options by accumulating the rewards obtained from each algorithm, identifying the most effective pricing strategies.

In the processing of the training dataset, the asUCB algorithm dynamically adjusted its confidence interval thresholds to balance the exploration of new knowledge and the exploitation of existing information. The research results show that this algorithm can effectively adapt to and simulate historical price trends within the training set, thereby proposing a robust pricing strategy. Notably, the UCB algorithm demonstrated rapid convergence and recorded lower cumulative regret metrics in various experimental scenarios (see Figure 1, Figure 2, Figure 3,Figure 4), highlighting its superiority in solving online decision-making problems.

The TS algorithm optimizes pricing strategies by generating probability distributions through sampling. Although initial price predictions may experience slight fluctuations, over time, the TS algorithm gradually converges to the optimal pricing strategy. Its performance in the training set also shows that it can effectively fit historical data, although its convergence is relatively slow, resulting in higher cumulative regret values (see Figure 1, Figure 2, Figure 3,Figure 5).

3.2. Simulation Set Performance

On the simulation dataset, we applied the best pricing strategies identified during the training phase to untrained data and observed the actual performance of the UCB and TS algorithms. Simultaneously, we adopted Mean Squared Error (MSE) as the metric to assess the accuracy of the model fitting.

3.2.1. Performance of the asUCB Algorithm

On the simulation set, the asUCB algorithm demonstrated good adaptability. The optimal pricing strategy determined by the asUCB algorithm resulted in an MSE of 276.29 in the simulation set, indicating the algorithm's effective capability to fit future price trends (see Figure 3).

Additionally, the UCB algorithm exhibited significant stability in responding to market fluctuations, ensuring consistency in pricing outcomes across various volatile scenarios.

3.2.2. Performance of the TS Algorithm

The TS algorithm had an MSE of 412.34 on the simulation set, slightly higher than that of the UCB algorithm, indicating its slightly inferior performance in fitting the test set data (see Figure 3).

Although the TS algorithm's performance in handling novel data was somewhat lacking compared to the UCB algorithm, its mechanisms for gradual optimization and self-adaptation endow it with unique application value in a rapidly changing market environment.

3.3. Comparison and Analysis

Based on the comparison of the performance of UCB and TS algorithms in the training dataset and simulation scenarios, the following core points can be summarized:

Based on the Mean Squared Error (MSE) metric, the UCB algorithm exhibited lower error values (276.29), suggesting it fits and performs better compared to the test data. In contrast, the MSE for the TS algorithm was 412.34, which, although slightly higher, still possesses the capability to effectively adapt and describe the data.

In terms of cumulative regret, the UCB algorithm demonstrated greater superiority compared to the TS algorithm. This finding implies that the UCB algorithm can more efficiently discover the optimal pricing strategy, thereby effectively reducing loss amounts in the decision-making process (see Figures 1, Figure 2 and Figure 3).

In terms of stability and flexibility: The UCB algorithm, due to its rapid convergence performance and lower regret values, shows exceptional stability and good fitting characteristics; whereas the TS algorithm displays unique advantages in adapting to the variability of market environments and its adaptive strategies.

3.4. Summary of Results

Upon comprehensive consideration, both UCB and TS algorithms demonstrate potential application value in the dynamic pricing domain for crops. Among them, the UCB algorithm, with its smaller MSE and better cumulative regret values, exhibits superior performance in model fitting accuracy and stability; while the TS algorithm, through its flexible sampling strategy, shows a degree of adaptability in responding to dynamic market changes.

The study results show that MAB algorithms can be effectively applied in the process of setting crop market pricing strategies and play a crucial role in grasping market dynamics and predicting future price trends. Future research could continue to explore the application potential of these algorithms in various market environments and consider integrating other machine learning techniques to enhance their performance.

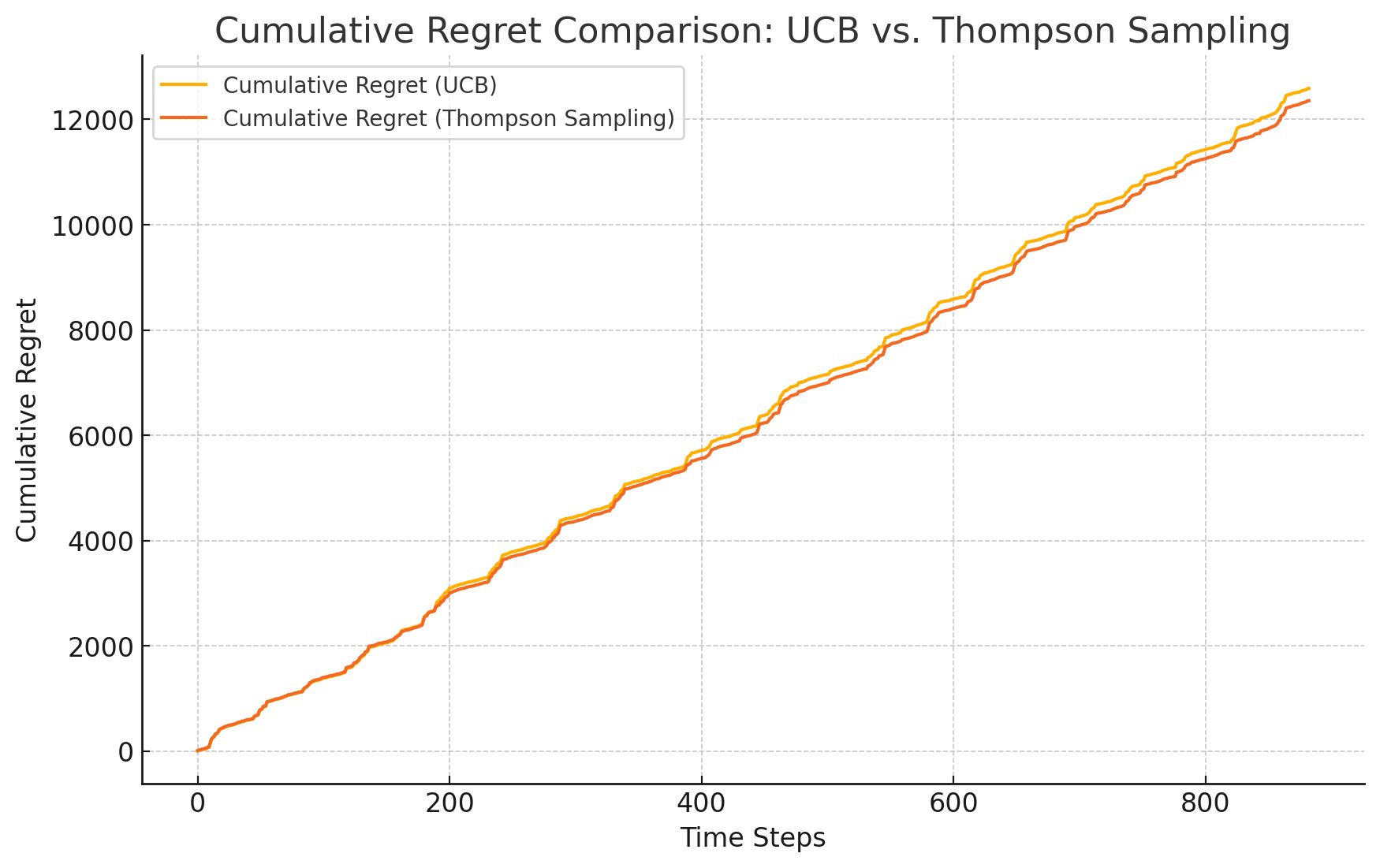
Figure 1. cumulative regret comparison: UCB vs. TS (1 time)

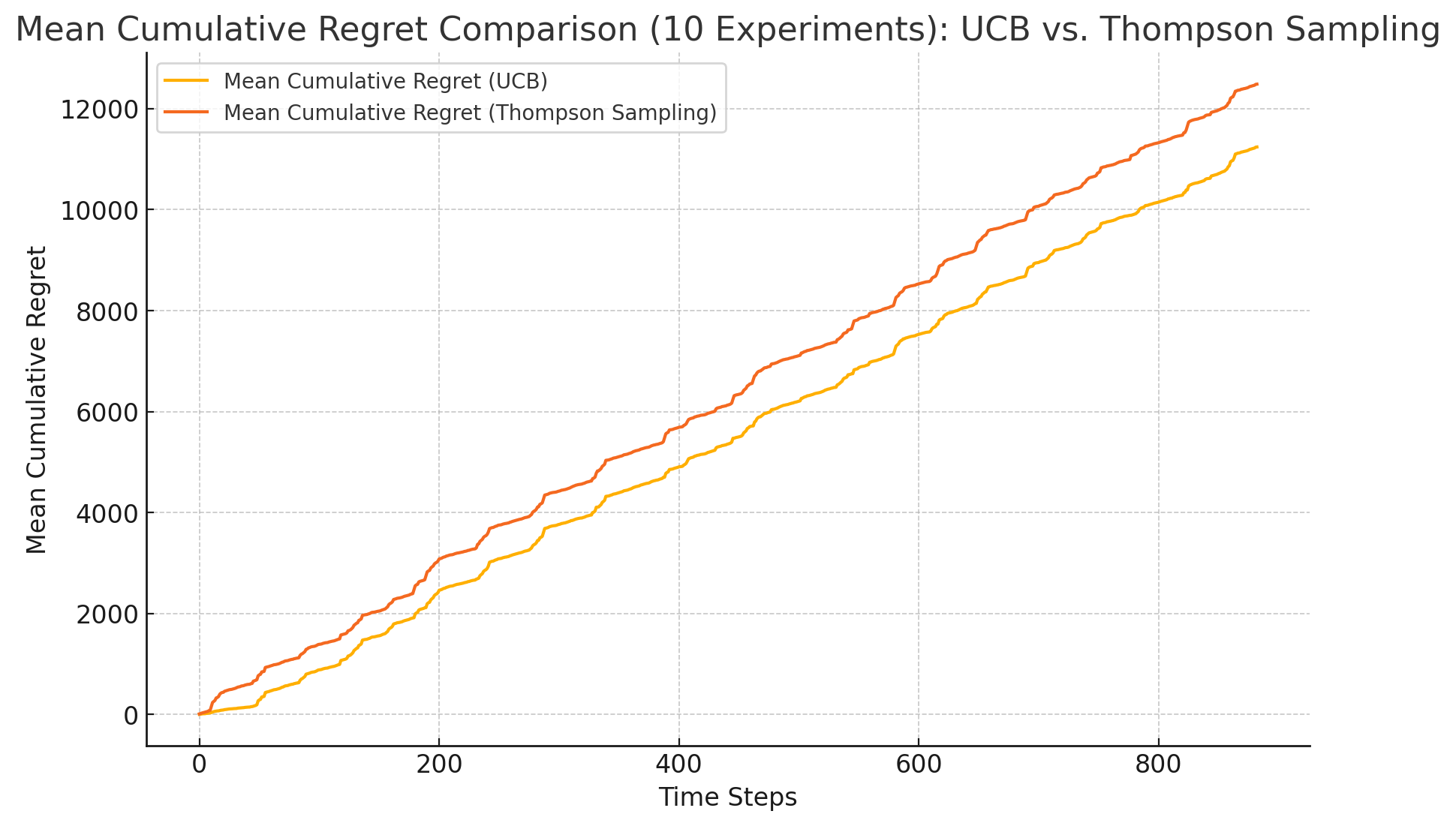
Figure 2. cumulative regret comparison: UCB vs. TS (10 time)

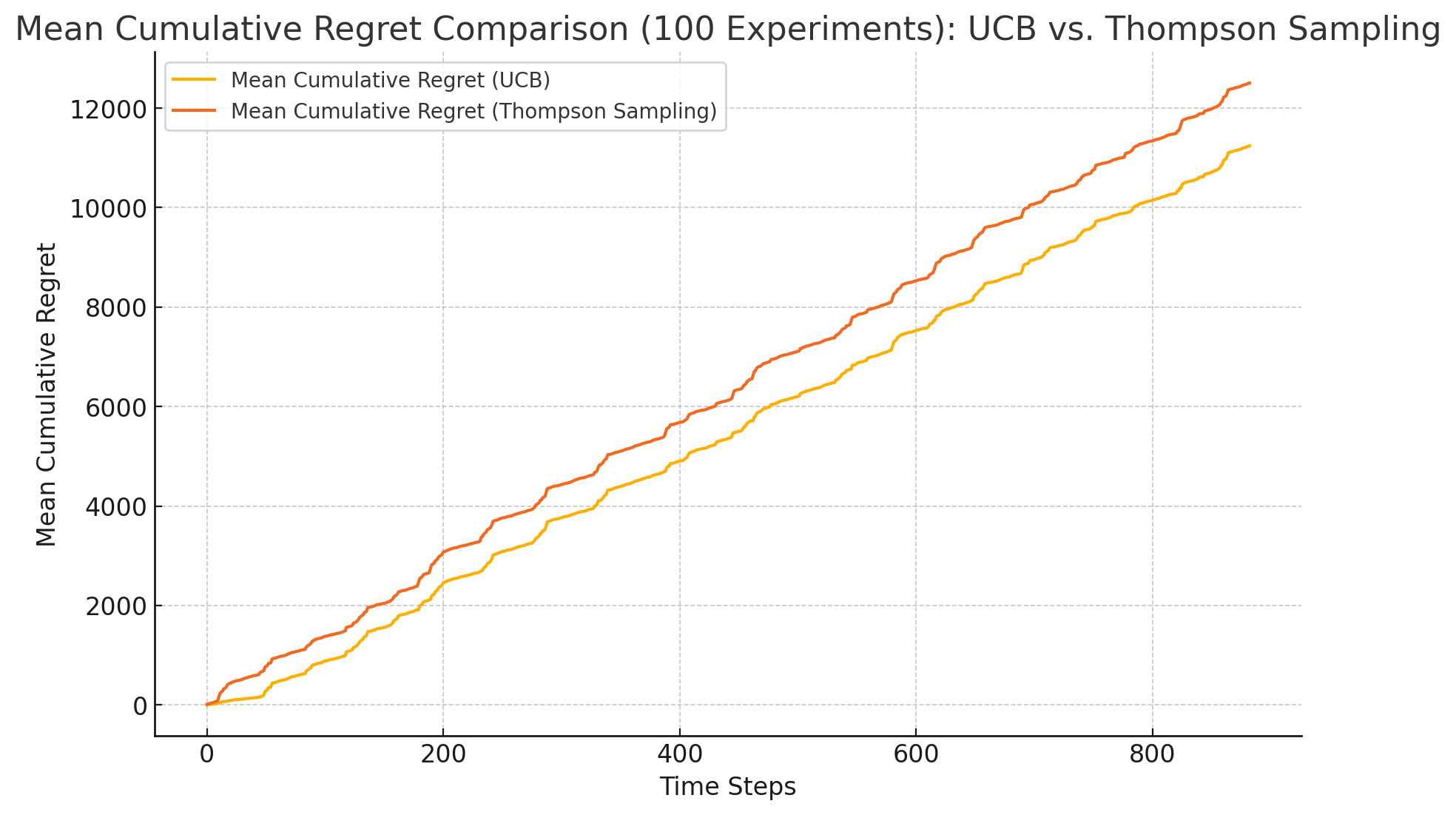
Figure 3. cumulative regret comparison: UCB vs. TS (100 time)

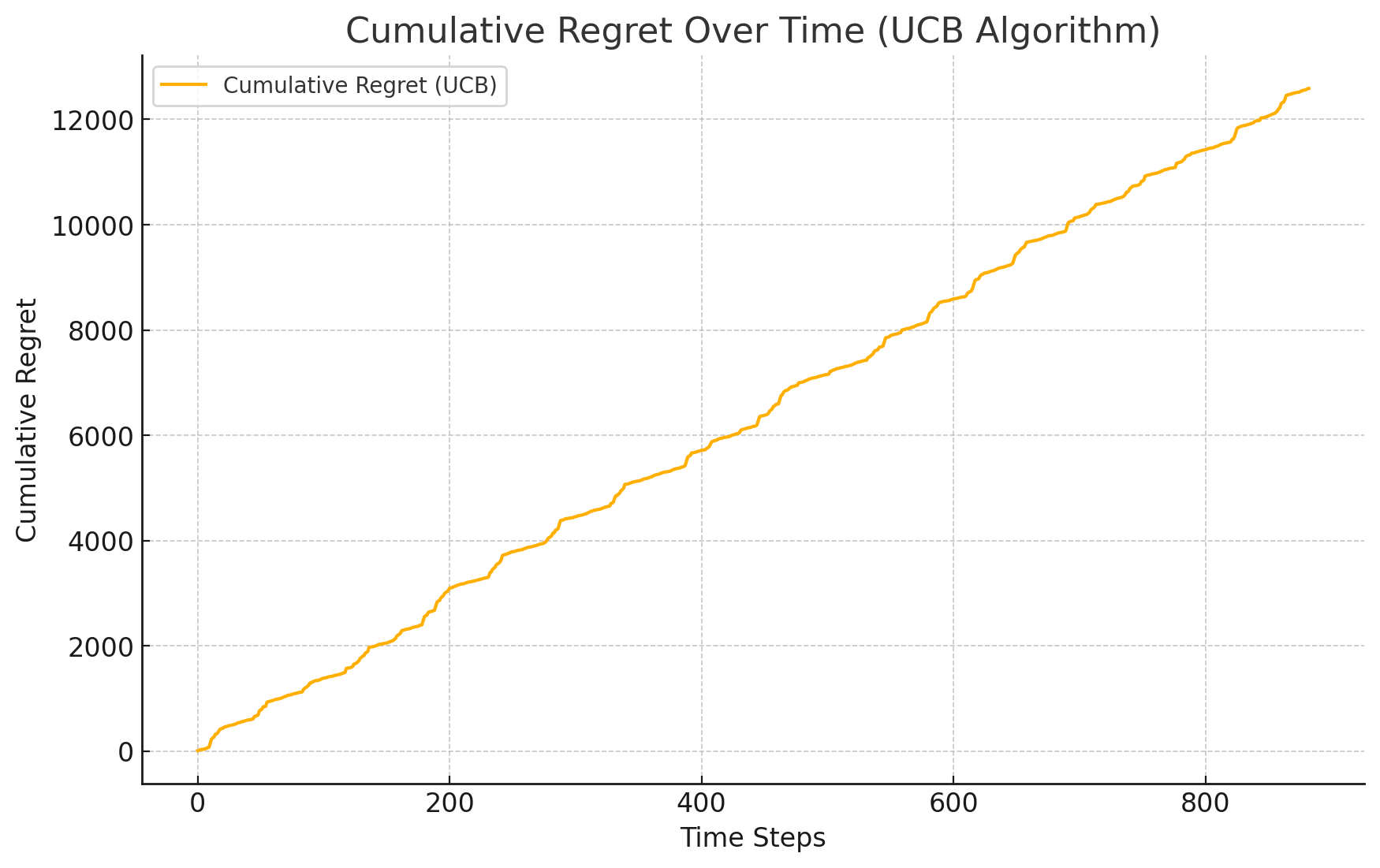
Figure 4. cumulative regret of UCB over time

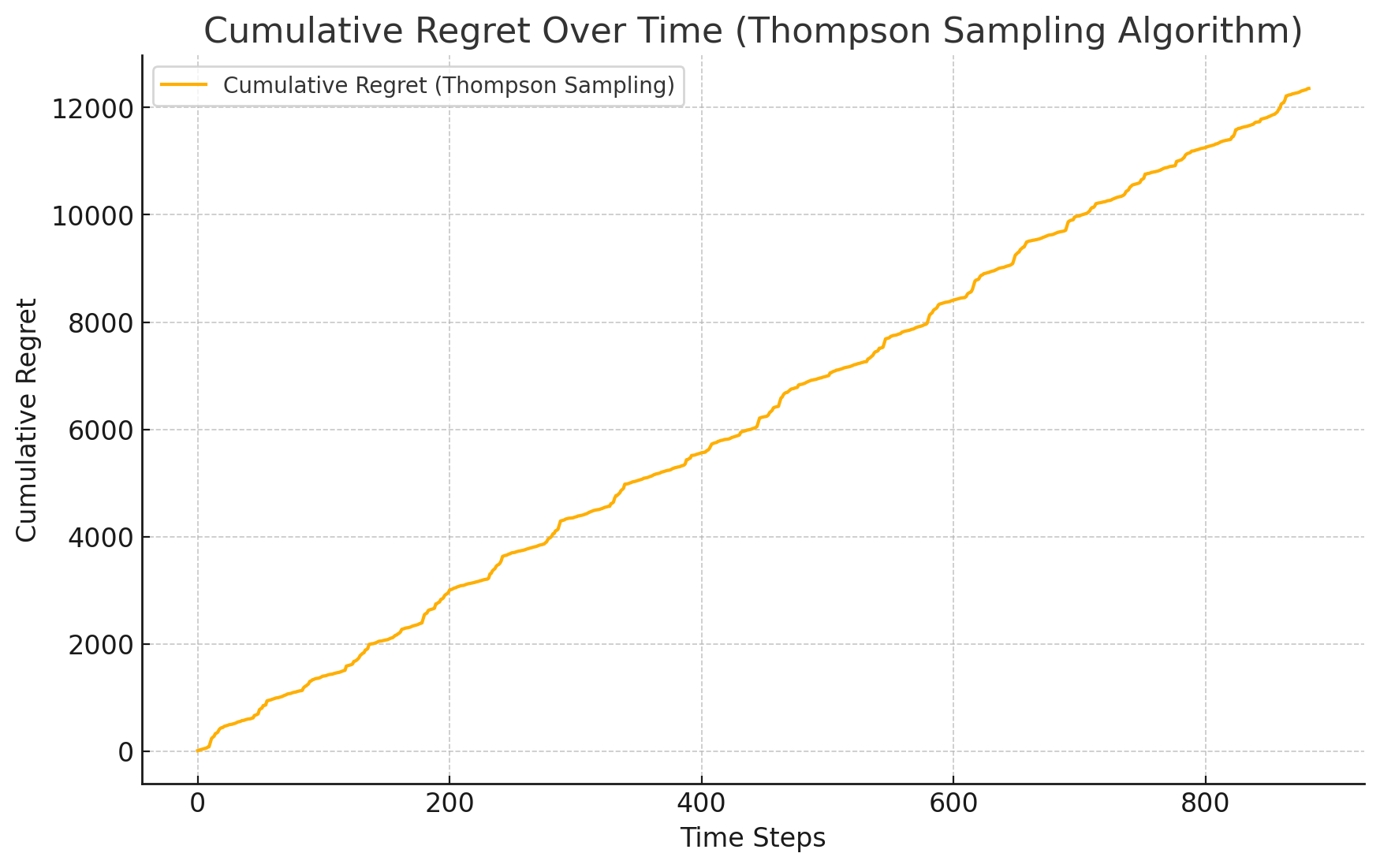
Figure 5. cumulative regret of TS over time

4. Conclusion and discussion

4.1. Summary of Experimental Results

In this study, we explored the application performance of multi-armed bandit (MAB) algorithms in dynamic pricing of crops, specifically focusing on the upper confidence bound adaptive algorithm (asUCB) and Thompson Sampling (TS). Our findings include:

Superiority of the UCB Algorithm: Compared to the TS algorithm, the UCB algorithm performed better in both the training dataset and simulation tests, specifically exhibiting lower Mean Squared Error (MSE) and fewer cumulative regrets. The algorithm demonstrated its rapid convergence and consistent stability, validating its applicability under volatile market conditions.

Adaptability of the TS Algorithm: Although the TS algorithm showed slightly inferior MSE and cumulative regret values compared to the UCB algorithm, its mechanism of guiding strategy selection through probability distribution sampling grants it unique flexibility and adaptability in dealing with market volatility and uncertainty. This feature allows the TS algorithm to continuously optimize and adjust its strategy over long time periods, even if its initial performance may not be as prominent as that of the UCB algorithm.

4.2. Comparison with Existing Research

The results of this study align with current academic perspectives and also offer new insights. Previous research has demonstrated the UCB algorithm's simplicity and efficiency, widely applying it in various contexts. Our experiments have further proven its exceptional performance in dynamic pricing. Moreover, the flexibility displayed by the TS algorithm in dealing with highly volatile market data reaffirms existing research findings.

4.3. Practical Application Significance

The outcomes of this research provide significant references for formulating price strategies in the actual crop market. The UCB algorithm, with its rapid convergence and robust performance, is suitable for scenarios that require quick responses to market dynamics, such as pricing strategies for seasonal agricultural products. In contrast, the TS algorithm shows its advantages in environments with high uncertainty and longer periods of adjustment, especially in the development of new markets or pricing strategies for highly volatile products.

4.4. Limitations of the Study

Although this study has achieved certain successes, it has several limitations. Primarily, the reliance on historical and simulated data may not fully capture the complex and variable characteristics of market environments, potentially weakening the general applicability of the conclusions. Secondly, the study was limited to two types of multi-armed bandit algorithms and did not explore potential advantages of more advanced strategies like hybrid strategies or deep reinforcement learning in specific scenarios. Additionally, the experimental design did not fully incorporate other key pricing factors such as consumer behavior and market competition, which could significantly impact the effectiveness of pricing strategies in real-world applications.

4.5. Directions for Future Research

Future research could delve deeper into several areas:

4.5.1. Exploring Algorithm Application Extensions

Future directions could include integrating other areas of machine learning, such as merging deep reinforcement learning with game theory, to address more complex and variable market situations and pricing challenges.

4.5.2. Comprehensive Multi-factor Analysis

Future studies could further explore factors such as consumer behavior characteristics and competitive market conditions, aiming to establish a more thorough and dynamically adjustable pricing mechanism model.

4.5.3. Multi-domain Adaptability of MAB Algorithms

Not only are these algorithms effective in regulating prices in the crop market, but they could also be extended to e-commerce and transportation industries to optimize dynamic pricing strategies. Future scholars could explore these cross-industry applications to fully validate the general utility and practical significance of MAB algorithms.

5. Conclusion

This study highlights the significant application prospects of UCB and TS algorithms in dynamic pricing for agricultural products, showcasing their robust performance, quick adaptation to market changes, stability in price setting, and suitability for dynamic agricultural markets. Conversely, the TS algorithm excels in uncertain environments by effectively adapting over time to optimize pricing strategies. The practical implications of this research are substantial as it provides insights into utilizing multi-armed bandit algorithms to enhance market responsiveness and pricing efficiency in agriculture. Notably, this study innovatively adapts these algorithms to simulate real-world scenarios, offering a novel approach that merges theoretical models with practical applications. However, it is important to acknowledge that reliance on historical and simulated data may not fully capture the complexity of real markets. Additionally, this study focuses only on two algorithm types while overlooking potential benefits from more advanced or hybrid strategies. Future research should aim at integrating advanced machine learning techniques to improve adaptability and accuracy of these algorithms. Furthermore, expanding their application across other industries such as e-commerce and transportation while incorporating factors like consumer behavior and competitive dynamics could provide deeper insights and more comprehensive pricing models. Enhancing the real-time responsiveness of these algorithms to market conditions would further validate their effectiveness in practical applications. Continued development holds immense potential for multi-armed bandit algorithms revolutionizing dynamic pricing strategies across various sectors.