1. Introduction

The Multi-Armed Bandit (MAB) problem is a fundamental framework in decision theory and machine learning that captures the essence of the exploration-exploitation trade-off. Originating from the analogy of a gambler faced with multiple slot machines (referred to as "arms"), each with an unknown probability distribution of rewards, the objective of the MAB problem is to develop a strategy that maximizes cumulative rewards over time. This challenge arises in various fields, including online advertising, clinical trials, and dynamic pricing, where decision-makers must continuously choose among competing options with uncertain outcomes.

The classical MAB problem has been extensively studied[1, 2], either for the methods to identify the best arm or different strategies to maximize the cumulative reward given conditions, leading to the development of numerous algorithms designed to balance the need for exploration (trying out different arms to learn about their rewards) and exploitation (choosing the best-known arm to maximize immediate reward)[3]. Among these researches, multiple powerful algorithms can solve an MAB problem efficiently[4]. But there is only a few of researchers have ever mentioned how to maintain the performance of an algorithm at a level when facing different variances in the distribution of the rewards, or how to get the lowest regret if we are testing on a reversed environment setup. The environment in which these algorithms operate can significantly influence their performance. Particularly, the nature of the reward distributions—whether they are dense (with small variance) or sparse (with large variance)—can pose unique challenges[5]. In dense environments, where the rewards of different arms are close in value, distinguishing between the best and suboptimal arms requires subtle exploration strategies. Conversely, in sparse environments, where some arms offer significantly higher rewards than others, the algorithm must efficiently identify and exploit these high-reward arms despite the noise introduced by large variance. There are several minimax optimal algorithms designed by other researchers for dealing with this kind of situation[6, 7].

In this paper, we will focus on The Minimax Optimal Strategy in the Stochastic (MOSS) algorithm, which has emerged as a robust solution within this context. MOSS is designed to perform well across various reward distributions by minimizing the worst-case regret—the difference between the reward collected by the algorithm and the reward of the optimal strategy. This minimax approach ensures that the algorithm remains effective even in the most challenging scenarios, making it particularly well-suited for environments with both dense and sparse reward structures[8, 9].

This research seeks to explore the application of the MOSS algorithm in both dense and sparse environments, analyzing its performance and adaptability in these contrasting settings. By understanding how MOSS navigates the complexities of varying reward distributions, this study aims to contribute to the broader field of bandit algorithms, providing insights that could enhance their applicability in real-world scenarios where reward variances play a crucial role[10, 11].

The significance of this research lies in its potential to bridge a critical gap in the application of bandit algorithms. While MOSS has been shown to perform well in theoretical analyses, its behavior in environments characterized by dense and sparse reward distributions warrants further exploration. By systematically studying these environments, this study aims to: Enhance the understanding of MOSS's robustness across different types of reward distributions; Provide practical insights for applying MOSS in real-world scenarios, particularly in domains where reward variances can be extreme; Guide the development of new algorithms that can better adapt to diverse environments, ultimately improving decision-making processes in various applications.

Through this research, the aim is to contribute to the ongoing development of more versatile and efficient bandit algorithms, thereby expanding their applicability in increasingly complex and uncertain environments.

2. The multi-armed bandit problem

This paper addresses the stochastic version of the multi-armed bandit (MAB) problem, where a machine with 18 arms must be played sequentially at each time step \( t=1, 2, 3,… \) . Each arm, when pulled, dispenses a reward derived from 1 to 5 with a fixed probability. These rewards are independent identically distributed and observable right after each play.

The strategy of the MAB algorithm is to select which arm to pull at every time step t, informed by the results of all previous \( t-1 \) lever pulls. The objective is to optimize the sum of expected rewards over T plays, i.e., \( E[\sum _{t=1}^{T}{μ_{i(t)}}] \) , where \( i(t) \) represents the arm chosen at time t. Here, \( {μ_{i}} \) represents the expected reward for arm i. The goal is typically to maximize the cumulative reward, making it practical to evaluate the algorithm's performance in terms of regret, a metric that reflects the regret incurred from not always choosing the best arm.

To elaborate on the notion of regret, let \( {μ^{*}} \) be the highest expected reward among all arms, and \( {∆_{i}}={μ^{*}}-{μ_{i}} \) ​ represent the regret associated with choosing arm i over the optimal one. Additionally, let \( {k_{i}}(t) \) denote the number of times arm i has been pulled up to time \( t-1 \) . The aggregate regret after T time steps, \( E[R(T)] \) , can then be defined as:

\( E[R(T)]=E[\sum _{t=1}^{T}{μ^{*}}-{μ_{i(t)}}]= \) (1)

2.1. Literature Review

The multi-armed bandit (MAB) problem has been widely studied due to its relevance to decision-making under uncertainty, particularly in fields such as machine learning, operations research, and recommended advertisements. The MAB problem focuses on the exploration-exploitation trade-off. By deciding between exploiting different unknown reward sources, people can discover higher payoffs potentially. There are several algorithms developed over the decades to tackle this problem, with each addressing different aspects of uncertainty, reward distribution, and computational efficiency.

2.1.1. Classical Algorithms

One of the earliest solutions to the MAB problem was the ε-greedy algorithm (Sutton & Barto, 1998). It emphasizes choosing a random arm with a small probability ε and selecting the arm with the highest expected reward otherwise to balance the trade-offs. This simple approach can indeed suffer from inefficiency, particularly in scenarios with non-stationary rewards or environments that require more adaptive strategies.

2.1.2. Bayesian Approaches

Bayesian methods have become popular for solving the MAB problem by using probability distributions to model uncertainty about rewards. The most famous Thompson Sampling(Thompson, 1933) maintains a posterior distribution over the expected rewards for each arm and selects arms based on sampling from these distributions. This algorithm has been shown to perform well in both stationary and non-stationary settings due to its natural incorporation of uncertainty. It is particularly effective when there is limited initial information, since the estimation of each arm’s average reward updates over time as the algorithm explore more which leads to improved decision-making.

2.1.3. Upper Confidence Bound (UCB) Algorithms

A major breakthrough in MAB algorithms came with the introduction of the Upper Confidence Bound (UCB) family of algorithms(Auer et al., 2002). The UCB algorithm selects arms based on both the estimated mean reward and an upper confidence bound that accounts for the uncertainty in the estimates. The original UCB algorithm uses the following criterion for selecting the i-th arm at round t:

\( {a_{t}}=arg{{max_{i}}({\hat{μ}_{i}}+\sqrt[]{\frac{2ln(t)}{{N_{i}}(t)}})} \)

where \( {\hat{μ}_{i}} \) ​ is the estimated mean reward for arm i, t is the total number of rounds played, and \( {N_{i}}(t) \) is the number of times arm i has been played. UCB is known for its logarithmic regret bounds in stationary environments. Several extensions of the UCB algorithm have been proposed to handle different reward structures, such as UCB1-Tuned, which adapts the confidence intervals based on the observed variance of rewards. UCB-based algorithms are particularly effective in scenarios with low variance rewards, where it is important to balance exploration efficiently with exploitation.

2.1.4. Algorithms for Adversarial and Non-Stationary Settings

In more complex environments, where the reward distributions may change over time or where adversarial conditions exist, classical algorithms often fail to maintain optimal performance. Algorithms like EXP3 (Exponential-weight algorithm for Exploration and Exploitation) have been developed for adversarial settings, where the rewards are not drawn from a fixed distribution but may be manipulated by an opponent. EXP3 uses a multiplicative weight update strategy and provides robust performance guarantees in such competitive environments.

2.1.5. Gaps and the Development of MOSS

While the above algorithms have made significant contributions to the MAB literature, many of them struggle in settings with unknown or large time horizons, as well as in environments where the variance of rewards is either very high or very low. Algorithms like UCB are well-suited for dense reward environments, but they may perform sub-optimally in sparse environments with high reward variability.

To address this, Minimal Optimal Strategy for Stochastic Bandits (MOSS) was introduced by Audibert and Bubeck. MOSS is designed to improve performance in environments where rewards are sparse or highly variable. Unlike classical UCB, MOSS applies an adjusted confidence bound that does not rely on prior knowledge of the time horizon, making it more robust in practical applications. MOSS also achieves near-optimal regret bounds across a wide range of settings, making it particularly useful in domains where classical UCB algorithms might struggle due to the unknown length of the decision process.

2.2. Methodology

To perform a more accurate experiment, this study designed each of the comparison algorithms in the following settings. In the ETC algorithm, this experiment dedicates 10% of the total trials (10,000 trials) to the exploration phase representing a strategic balance. This allocation is designed to optimize the trade-off between the inherent regret incurred during the exploration period and the benefits gained from accurately identifying the most rewarding arm to commit to in subsequent trials. By limiting the exploration phase to 10%, ETC efficiently utilizes enough trials to gather sufficient data on the performance of each arm, without excessively prolonging the exploration at the expense of exploiting the best-performing arm. The reason for choosing this proportion is particularly advantageous as it provides a substantial sample size to overcome variability while preventing the waste of opportunities to accrue rewards from the best arm.

In the UCB and the AO-UCB algorithm, this research chooses \( l=4 \) as a parameter setting that plays a critical role in enhancing the algorithms' exploration capabilities. By setting l at this level, the exploration term in the formula \( \sqrt[]{\frac{l∙log(t)}{{n_{i}}(t)}} \) is amplified. This significantly increases the algorithms' propensity to explore those less frequently chosen arms, giving a balanced compromise between excessive exploration and sufficient exploitation. This heightened exploration is beneficial in environments where the reward distributions are highly variable, as it allows the algorithms to gather more comprehensive data about all available options. Thus choosing \( l=4 \) provides a well-considered balance that leverages aggressive yet controlled exploration to optimize performance in stochastic settings.

2.3. MOSS

Firstly, let us outline the MOSS (Minimax Optimal Strategy in the Stochastic case) algorithm for the multi-armed bandit problem, where each arm i of a slot machine yields a reward within [1, 5] that follows a fixed distribution each in a sparse and dense environment​. This paper also introduces a feature of this algorithm that makes it handle welly to complex environments of the distribution of the rewards between different arms, enabling its application to a broader range of stochastic bandit problems.

MOSS maintains a non-Bayesian approach, focusing on achieving minimax optimal regret, which is effective for settings with unknown reward distributions. Recall that the regret in the multi-armed bandit problem is defined as the difference between the expected total reward from always playing the best arm and the expected total reward from the strategy employed by the algorithm. This framework is advantageous for bandit problems as it leads to robust strategies across different variance levels of rewards.

The mathematical foundation of MOSS is encapsulated by the minimization of the upper bound of cumulative regret. This upper bound is calculated as:

\( R(T)=O(\sqrt[]{KTlog{T}}) \) (2)

where K is the number of arms, and T is the number of time steps. MOSS optimizes the allocation of plays among the arms to minimize this upper regret bound. The selection mechanism for each arm is adapted at each step by estimating the lower confidence bound of the expected rewards, which is adjusted for each arm based on the number of times it has been played:

\( {B_{i}}(t)={\hat{μ}_{i}}(t)-\sqrt[]{\frac{3log{(t)}}{2{k_{i}}(t)}} \) (3)

where \( {\hat{μ}_{i}}(t) \) is the empirical mean of the rewards obtained from arm i, and \( {k_{i}}(t) \) is the number of times arm i has been played up to time t. The arm with the highest value of \( {B_{i}}(t) \) is chosen to balance the exploration and exploitation trade-off. The algorithm of MOSS is summarized as below.

Algorithm: MOSS for Stochastic Bandits

Initialize:

total_count=0

estimates[]=0 for all i (estimates of rewards)

counts[]=0 for all i (count of selections for each arm)

regrets[] (to track cumulative regrets)

ucb_list[]=0 for all i (upper confidence bounds)

foreach t=1, 2, …, num_steps:

if total_count < K:

k=total_count

(exploration phase)

else:

k=argmax(ucb_list[i])

(exploitation phase)

estimates[k] += \( \frac{r-estimates[k]}{counts[k]} \)

ucb_list[k] = estimates[k] + \( \frac{B}{2}×\frac{\sqrt[]{4×log⁡(max⁡(1, num\_steps/(K×counts[k])))}}{counts[k]} \)

update total_count, counts[k], and regrets[k] repectively

End Loop

3. Experiment Design

Two environments of stochastic stationary bandits are established, with fixed reward distributions for each arm in both environments. This paper only considers dense and sparse environments because they are the two most common features of datasets in the real world and all kinds of problems are of the same category by them.

3.1. Dense and Sparse Environment

In the context of multi-armed bandit problems, we refer to a dense environment as a scenario where the reward of available arms has less standard deviation, as the true mean reward of each arm is close to each other. The challenge intensifies as the algorithm must make decisions from a substantially larger set of options with limited opportunity to sample each one thoroughly. This increases the complexity of achieving optimal exploration and exploitation, as the probability of selecting the best arm decreases and the need for effective decision-making strategies becomes critical. The dense dataset of this study is shown in Figure 1.

Sparse environments present a contrasting scenario where there is a limited amount of arms that have great true mean rewards, while most of the others have significantly smaller true mean rewards compared to those. In such settings, the regret from choosing suboptimal arms can be affected badly, making the algorithm have a larger overall regret. But with the right exploration method, it might enhance the algorithm’s ability to explore each arm thoroughly facilitating a more robust estimation of the reward distributions and potentially leading to more effective exploitation of the best-performing arms. The sparse dataset of this study is shown in Figure 2.

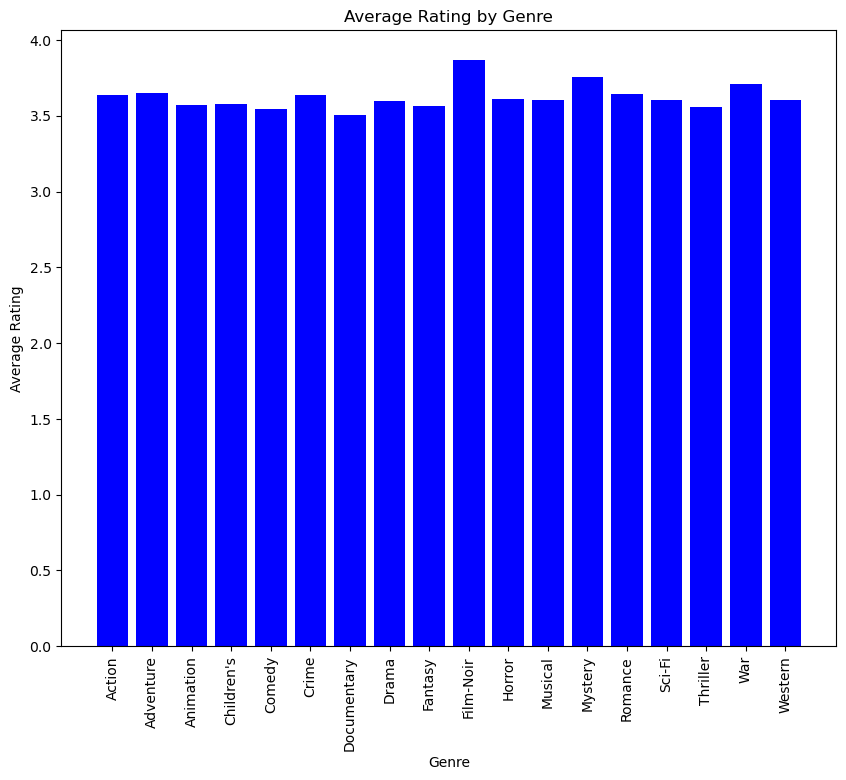
Figure 1. Average rating of each genre from Figure 2. Average rating of each genre from

on all movies in the dense environment. on all movies in the sparse environment.

The reason for choosing these two environments is to illustrate the robustness of the MOSS algorithm, testing which algorithms mentioned before have the best overall performance when facing the two kinds of datasets.

3.2. Method

To illustrate the advantage of the MOSS algorithm, comparison plots among ETC, UCB, AO-UCB, TS, and MOSS will be drawn, by setting the number of trials to 100000 and comparing the cumulative regret of all five algorithms.

To mitigate the effects of randomness and enhance the reliability of the findings, 10 independent experiments will be conducted to calculate the average regret. This approach is crucial because randomness in experimental outcomes can lead to variability which results in incorrect conclusions. Since each experiment involves stochastic elements—the random selection of movie ratings is based on their probability distribution, which can introduce noise into the results. By running multiple independent trials and averaging their outcomes can efficiently reduce the influence of any single outlier caused by chance. This method averages across experiments helps to smooth out anomalies and provides a more accurate estimation of the algorithms’ expected behavior under typical environments.

4. Results

Figure 3 is the curve of cumulative regret with respect to the number of trails in dense environment. The blue curve is ETC, orange is UCB, green is AO-UCB, red is TS, and the purple is MOSS.

Figure 4 is the same curve of the left but tested on sparse environment to prove that the MOSS is also \( O(\sqrt[]{KTlog{T}}) \) and robustness. Note that in both graphs MOSS outperforms all the algorithms when the trails are large enough (total trails 100000 here with averaging 10 experiments).

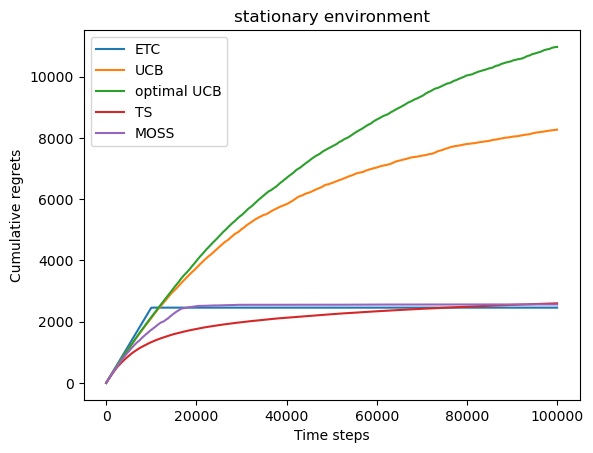
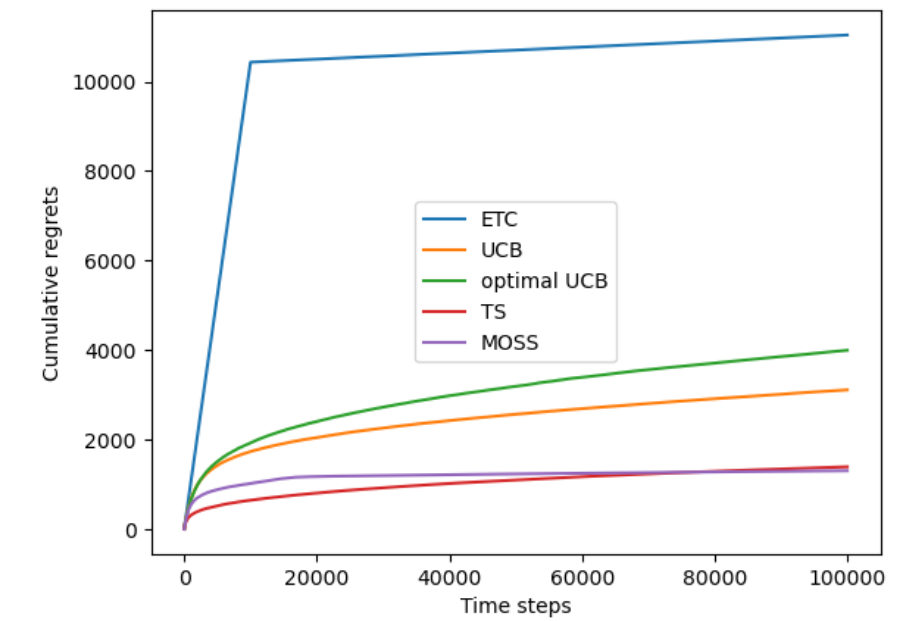
Figure 3. Cumulative regrets in each trail Figure 4. Cumulative regrets in each trail

of the five algorithms in dense environment. of the five algorithms in sparse environment.

To look more closely at the graph, a better way is to extract the cumulative regrets of each algorithm at the very last round and make them in the Table 1.

Table 1. Cumulative regret of five algorithms on different environments.

In the dense environment, MOSS performs well with a cumulative regret of 2563.07, indicating its robustness in settings with small reward variance. ETC seems to have a smaller cumulative regret but with the increase of experiments, the average regret over experiments increases since it has the potential to choose the sub-optimal arm in the commit phase. UCB and AO-UCB struggle significantly in this environment, while TS shows moderate performance. In the sparse environment, where the variance in rewards is larger, ETC’s performance deteriorates with a high regret, whereas both UCB and AO-UCB show improvements. TS adapts well to the sparse environment, but MOSS again demonstrates superior performance with the lowest cumulative regret of 1292.30. These results underscore the consistent effectiveness of MOSS across varying environments, highlighting its adaptability and robustness in comparison to other algorithms.

4.1. Time comparison

Besides the regret, a timer is set for each algorithm to compare their running time. The running time in seconds represents the average time to run one experiment for each algorithm in ten experiments with different environments, as shown in Table 2 below.

Table 2. Average running time of five algorithms on different environments.

Table 2 indicates that the MOSS algorithm has a similar running time to UCB, both in dense and sparse environments, with MOSS slightly slower by only 0.03 units in the dense and 0.03 units in the sparse environment. However, MOSS is significantly faster than TS, which takes around 10.39 and 10.98 units of time in dense and sparse environments, respectively. This suggests that the MOSS algorithm is more time-efficient while still maintaining strong performance across different environments, making it a practical choice when both efficiency and effectiveness are critical.

5. Result analysis

MOSS adjusts the exploration-exploitation balance using an upper confidence bound that is more conservative compared to classical UCB. The upper confidence bound for each arm i at time t in MOSS is defined as:

\( {MOSS_{i}}(t)={\hat{μ}_{i}}(t)+\sqrt[]{\frac{log{(\frac{T}{{K_{i}}(t)})}}{{K_{i}}(t)}} \) (4)

Here the function has \( {\hat{μ}_{i}}(t) \) denoted the empirical mean reward of arm i up to time t. T is the total number of plays, and \( {K_{i}}(t) \) denoted is the number of times arm i has been played up to time t.

In the initial stages, all arms have been played a few times, making \( {K_{i}}(t) \) relatively small. Consequently, the term ​ \( \frac{log⁡(\frac{T}{{K_{i}}(t)})}{{K_{i}}(t)} \) is large, resulting in a significant exploration bonus. This drives the algorithm to explore each arm more thoroughly, ensuring no potentially optimal arm is overlooked early on. As \( {K_{i}}(t) \) increases with ongoing plays, the exploration term \( \sqrt[]{\frac{log⁡(\frac{T}{{K_{i}}(t)})}{{K_{i}}(t)}} \) gradually decreases. This reduces the emphasis on exploration directly proportional to the increase in confidence regarding the empirical mean estimates \( {\hat{μ}_{i}}(t) \) , as the transition observed in the cumulative regret graph reflects this decrease in exploration intensity. Then MOSS begins exploiting arms that offer higher rewards more frequently, leading to a slowing rate of increase in cumulative regret in the later part. Further, the feature of logarithmic scaling of the exploration term in MOSS ensures that even as time progresses, the algorithm maintains a non-trivial degree of exploration. This is particularly effective in environments where the variance of rewards is not drastic. Hence, MOSS continues to fine-tune its estimates and occasionally explores less-chosen arms, safeguarding against premature convergence to suboptimal choices.

The logarithmic factor in the exploration term of MOSS ensures that the exploration is not only tied to the absolute number of times an arm has been played but also to the ratio of total rounds to individual arm plays. This unique approach helps in balancing exploration and exploitation more effectively over a long horizon compared to other algorithms that might either explore too much or too little. MOSS is designed to minimize the worst-case regret, making it robust in environments with uncertain or dynamic reward distributions, as it avoids overly rapid convergence on potentially misleading early results. The performance of the MOSS algorithm that was observed in the cumulative regret values above for both dense and sparse environments reflects its strategic design to minimize worst-case regret over a long horizon.

If we look again at Figure 3 and Figure 4, in dense environments where the variance of each arm’s reward is small, MOSS initially incurs a higher regret as it strives to equally explore all arms to ensure robustness against worst-case scenarios. This feature causes MOSS to perform slightly worse at the beginning but improves significantly as the trials continue, allowing it to gather sufficient information to make more informed decisions, ultimately leading to lower cumulative regret compared to algorithms that might favor early exploitation, such as the ETC or UCB. While in sparse environments, the larger variance of arm’s reward allows MOSS to complete its exploration phase more quickly and transition sooner to exploiting the best-performing arm. This results in more efficient performance and a markedly reduced cumulative regret, as evidenced by its comparative results. Thus, MOSS’s methodological balance between exploration and exploitation tailored to the number of available arms and the length of play significantly impacts its performance, making it a robust choice in scenarios where a careful exploration is crucial.

6. Conclusion

Based on the experiments conducted, the advantages of the MOSS algorithm can be summarized as follows: First, the regret of the MOSS algorithm is logarithmic in theory and smaller than UCB with the same parameter l in general, and it is even better than TS when the number of trails is large enough; Second, the MOSS algorithm is more adaptive to different environments than all other algorithms talks above; Third, the MOSS algorithm has a similar running time to UCB, which is much faster than TS.

Further, MOSS is particularly well-suited for dynamic environments where decisions must be made under uncertainty, such as personalized recommendation systems, clinical trials, real-time bidding in advertising, and autonomous systems in robotics. For instance, in e-commerce, MOSS could dynamically adjust to evolving consumer preferences to optimize product recommendations, enhancing user engagement and sales. In medical settings, it could streamline the allocation of treatments in clinical trials to quickly identify the most effective therapies, thereby improving patient outcomes. Future research could focus on adapting MOSS to handle non-stationary reward distributions and complex reward structures, potentially integrating machine learning techniques to predict optimal exploration phases, thereby broadening its utility across more complex scenarios.

Some limitations of the MOSS algorithm include that when the number of trials is small, its performance may be less favorable than that of TS. This is reasonable. Initially, TS employing a probability matching strategy, aggressively explores the action space through its Bayesian updating mechanism, which can lead to early identification of optimal arms. Conversely, MOSS starts with less aggressive exploration, focusing on minimizing worst-case regret through deterministic confidence intervals that tighten with more data, leading to potentially higher initial regret. Over time, MOSS's methodical exploration based on actual arm performance reduces exploration of suboptimal choices, concentrating on exploiting the best-performing arms. This strategy, aimed at robustly minimizing regret in the long run, becomes increasingly effective over a larger number of rounds, enabling MOSS to surpass TS in cumulative performance, particularly in environments where many interactions are expected and robust performance is critical.