1. Introduction

Quantum computing has emerged as a transformative technology, reshaping our understanding of computational problem-solving capabilities beyond the classical paradigms established in the last century. The early computational complexity theories, which arose around the 1960s, have formed a crucial backbone for the ongoing evolution of computer science, affecting numerous fields from cryptography to algorithmic theory [1]. As quantum computing began to materialize, it introduced the need for a new theoretical framework that would account for quantum phenomena under computational constraints, leading to the birth of quantum complexity theory. This novel domain has particularly focused on the capabilities and limitations of quantum systems in solving computational problems, providing a rigorous theoretical foundation for next-generation computational technologies.

As we advance further into the quantum computing era, the development of Noisy Intermediate-Scale Quantum (NISQ) devices presents new challenges and opportunities. Unlike ideal quantum computers, NISQ devices operate under significant noise and hardware limitations, necessitating the development of hybrid algorithms that combine classical and quantum computational processes [2]. This era of quantum technology not only tests the boundaries of quantum error correction but also propels the refinement of quantum complexity theory. The ongoing research in this field is aimed at understanding the practical thresholds and the theoretical implications of quantum computing, reflecting on how these insights can be leveraged to accelerate advancements in the field [3].

This paper aims to provide a comprehensive introduction to the current state of quantum complexity theory, emphasizing its application to NISQ devices and the broader implications for quantum computing. It outlines the progression from theoretical constructs to practical implementations, illustrating how classical complexity classes such as P, NP, and BQP are being expanded and redefined through the lens of quantum mechanics [4-6]. Additionally, this work explores significant algorithms that have shaped the field, such as Shor’s factoring algorithm and Grover’s search algorithm, highlighting their impact on the understanding of quantum computational limits and the design of quantum algorithms. Through a detailed analysis of current NISQ technologies and hybrid quantum-classical computational models, this paper seeks to delineate the evolving landscape of quantum complexity theory and its pivotal role in navigating the future trajectories of quantum computing technology.

2. Quantum computing fundamentals

2.1. Principles of quantum computing

Quantum mechanics describes the physical phenomena of microscopic objects. It is difficult to measure the exact properties of quantum particles and instead these properties are expressed via a probabilistic approach. The interaction between systems of particles also create states of superposition where there are many states that coexist with some probability.

Quantum computing is the study of quantum computing devices, namely devices that exploit and manipulate quantum physical objects to represent quantum states mathematically. The point is to harness the power of quantum mechanics, abusing superposition and resonance, in order to gain computational power.

2.2. Quantum states and qubits

Qubits are the fundamental information object of quantum computing, similar to the bit in classical computing. The qubit is capable of retaining much more information through its probabilistic state of superposition compared to the deterministic classical bit.

Qubits can be mathematically represented in terms of two orthonormal bases as:

|ϕ⟩ = α |0⟩ + β |1⟩ where |0⟩ = $(\frac{1}{0})$ and |1⟩ = $(\frac{0}{1})$ (1)

Where α2 and β2 are respectively the probabilities of the qubit to collapse to the states of |0⟩ and |1⟩ upon measurement.

Generally qubits are manipulated on in similar methods as the bit in classical computing, using quantum gates that preserve certain properties of qubits similarily to classical gates. These gates can be mathematically represented as unitary matrices, which are matrices that preserve the 2-norm:

||Ux||2 = ||x||2 (2)

where U is a unitary matrix for x in Cⁿ.

An example of a common unitary/quantum gate is the CNOT gate, which for two qubits |ϕ⟩ and |ψ⟩ operate on their combined state |ϕ⟩ ⊗ |ψ⟩:

CNOT $= ⌊ \begin{array}{c} \begin{array}{c} \begin{matrix}1 & 0 \\ 0 & 1 \\ \end{matrix} \begin{matrix}0 & 0 \\ 0 & 0 \\ \end{matrix} \\ \begin{matrix}0 & 0 \\ \end{matrix} \begin{matrix}0 & 1 \\ \end{matrix} \end{array} \\ \begin{matrix}0 & 0 \\ \end{matrix} \begin{matrix}1 & 0 \\ \end{matrix} \end{array} ⌋$ (3)

A quantum circuit is composed of many of these common gates (henceforth referred to as unitary matrices, or unitaries) together operating on a state composed of many qubits. A quantum algorithm relies on selectively choosing a combination of the correct unitary gates to pass qubit states through in order to manipulate them into a desired result.

Designing clever combinations of unitary operating gates to exploit the qubit systems’ ability to abuse quantum superposition is the key to achieve superior computational capabilities compared to classical systems. Investigating and designing such combinations and algorithms are the basis of quantum computing.

The crux of quantum complexity theory is then to analyze the computational limitations of these quantum circuit algorithms, similar to how classical complexity analyzes resource limitations of classical algorithms. It is then possible to contextualize the differences between quantum computing and classical computing with a rigorous framework.

3. Classical complexity classes

3.1. Definitions

To introduce quantum complexity theory we need to introduce some complexity classes in the classical sense first:

P is the class of languages L ⊆ {0, 1} ∗ for which there exists a deterministic turing machine M that for inputs of x ∈ {0, 1} n, M terminates in q(n) time where q is some polynomial and accepts x iff x ∈ L.

PSPACE is the class of languages defined similarily to P, however instead of a constraint on time there is only a polynomial constraint on the amount of space used to q (n). Naturally this class is much more powerful as it contains many algorithms that are not restricted by time complexity.

EXP is the class of languages L ⊆ {0, 1} ∗ for which there exists a deterministic turing machine M that for inputs of x ∈ {0, 1} n, M terminates in 2q (n) time where q is some polynomial and accepts x iff x ∈ L. So in essence it is P, but with exponential time instead of polynomial.

BPP is the class of languages L ⊆ {0, 1} ∗ for which there exists a probabilistic turing machine M that for inputs of x ∈ {0, 1} n, M terminates in q(n) time where q is some polynomial.

If x ∈ L, M accepts with probability > $\frac{2}{3}$ .

If x ̸∈ L, M accepts with probability < $\frac{1}{3}$ .

The probability constants 1 or 2 here does not actually matter, since we can continue running the turing machine a constant number of times and take the majority output to manipulate the accept probability, as running the algorithm a large constant of times does not bring it beyond polynomial time constraint.

3.2. Class relationships

In general, P ⊆ BPP ⊆ PSPACE ⊆ EXP, however the strictness of the relations are difficult to prove. Some of these relations are trivially true, while some of the others may require more rigorous computation and is beyond the scope of this report. A point of interest is that although these complexity classes are formally defined in the format of a decision problem, via sets of languages. However, many other problems such as search and optimization can often be reformulated as decision problems, and vice-versa, and we will generally refer to all of these problems to be bound within the complexity class’ restraints, rather than just strictly limit the definition to just decision problems.

4. Quantum complexity theory

4.1. BQP

BQP is the class of languages L ⊆ {0, 1} ∗ for which there exists some classically reproducible polynomial sized quantum circuits {Cn} that are built upon universal gates that for inputs of x ∈ {0, 1} n, for q some polynomial.

If x ∈ L, Cn(|0⟩⊗q(n)) accepts with probability > $\frac{2}{3}$ .

If x ̸∈ L, Cn(|0⟩⊗q(n)) accepts with probability < $\frac{1}{3}$ .

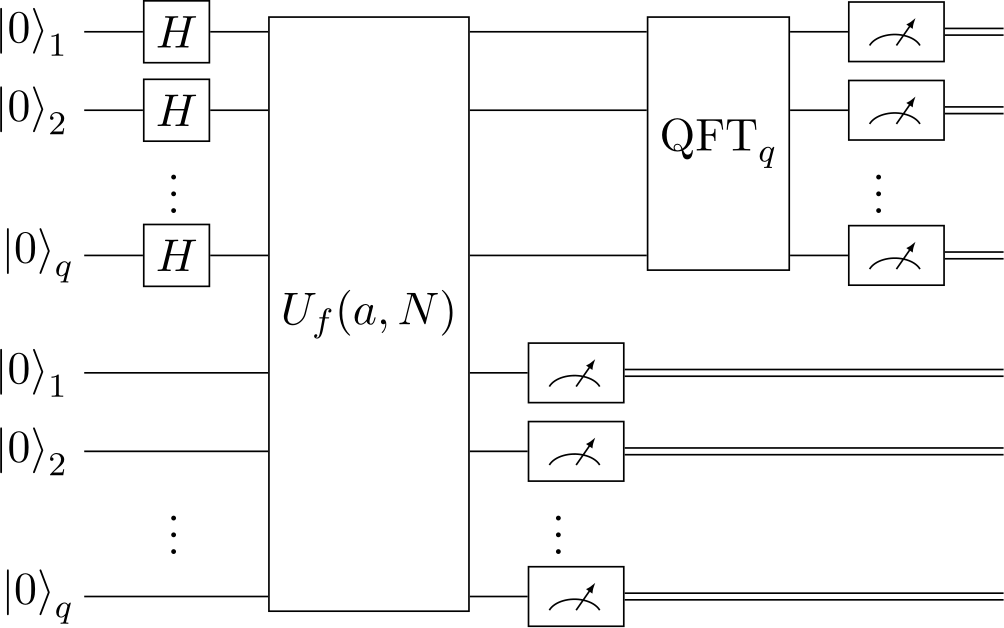
Figure 1. A circuit diagram of shor’s quantum period finding subroutine used for factoring (Photo credit: Original).

As show in the figure 1. An intuitive description of BQP is the class of decision problems solvable on a quantum turing machine within polynomial time with some bounded probability. Similar to BPP the probability does not matter, proved in Bennett’s past work [7].

BQP is the quantum analog of BPP [8, 9]. The relationship between BQP and its classical analogs have been proved to be BPP ⊆ BQP ⊆ PSPACE. Whether or not BPP = BQP remains to be proved. In general, BPP is the class of efficiently computable problems on a classical computer, and BPP ⊆ BQP demonstrates the advantage of quantum computers having a wider set of efficiently computable problems [10]. It remains to be discovered which problems are in the separation between BPP and BQP.

4.1. Important results in quantum complexity

One of the most important results in separation of BPP and BQP is Shor’s factoring algorithm [11]. Shor demonstrates a solution to the factoring problem with a reduction of the problem to an order-finding problem then providing a polynomial-time quantum subroutine that solves the reduced problem. The important result is that Shor demonstrates that the factoring problem, a problem that is not worst-case solvable in polynomial time can be solved efficiently in quantum computing.

Shor’s algorithm has since been experimentally implemented on modern quantum devices [12, 13]. Efficient factoring in particular is an incredibly important subject in the field of cryptography, where Shor’s algorithm has proved to be an exciting breakthrough [14]. Within the field of quantum complexity, this indeed shows Factoring ⊆ BQP.

Another interesting result is Grover’s search algorithm, with provides a quadratic speedup to unstructured search using a quantum algorithm. BBBV further proved that it is impossible to provide more than a quadratic speedup through a quantum speedup, and that Grover’s algorithm is indeed optimal [15].

Physical implementation of Grover’s algorithm on quantum devices continues to be an exciting point of research, especially successful implementation of the algorithm on modern devices, which contain noise and perturbations without the flawless error correction of a theoretical quantum turing machine [16].

5. NISQ complexity

Much of the work in the previous section discuss the theoretical framework of quantum complexity theory with theoretically ideal quantum turing machines. Our current ability to develop large scale quantum computers capable of supporting a large number of qubits is inadequate; it remains a challenge to maintain qubit systems in large scale in engineering.

One of the principle challenges of quantum computing is error correction for noisy qubits. Due to engineering challenges it is difficult to have noiseless quantum machines that are of a decent scale to run algorithms on; it is relatively simple for the physical systems that encode the qubit’s information to become perturbed by environmental factors that are difficult to control.

Noisy Intermediate-Scale Quantum (NISQ) technologies refer to the quantum devices available with our current engineering constraints [17]. Noisy quantum devices with a small yet sizable number of qubits, typically anywhere between 50-1000 qubits constructed. The term was coined to describe most quantum devices that current technology allows to be built. Current development of NISQ algorithms are generally hybrid algorithms where a classical algorithm has access to an imperfect quantum subroutine.

NISQ as a complexity class can generally be defined informally as the class of problems solvable on a classical probabilistic turing machine that has access to a noisy and small scale quantum devices, which can be loosely defined as a quantum computer with:

Polynomial input size of 0-qubit strings, which may be perturbed by noise.

Polynomial sized quantum unitaries with entries or results tampered with by noise.

Chen and al formally define NISQ in their supplementary work.

Generally, analysis of NISQ algorithms in specific cases is the leading work for within this field. For unstructured search, NISQ fails to achieve quadratic speedup like Grover’s algorithm. While on the other hand, for the Bernstein-Vazirani problem over n-bits, it is shown the original algorithm is robust enough to be noise resistant and still provide significant speedup over the classical counterpart with using an NISQ algorithm.

Generally the algorithms in the NISQ era are conducted with a classical-quantum hybrid with the classically difficult part that can be optimized done on a quantum device, hoping to achieve considerable speedup due to the separation of BQP and BPP. It has also been shown there exists separation between NISQ and BPP, as well as NISQ and BQP. Which problems can be efficiently solved lie between these complexity classes is to be investigated.

Most of the algorithmic research related to NISQ as a complexity class work with variational quantum algorithms (VQAs), which are algorithms which encode a problem into an optimization objective function, choose a parametrized quantum circuit (PQC) as the ground state typically a 0-qubit string, and then attempt to solve the optimization problem using the state space of the PQC using a hybrid algorithm. A plethora of works regarding the uses of this style of quantum annealing approach as well as investigation into physical implementation have concluded that: It is difficult to expect quantum computing, in its limited form, to arrive at optimal quantum speedups with fault intolerant algorithms, algorithms must be design to take accountability of always-present noise.

It is unknown outside of specific fields such as cryptography if NISQ algorithms can have significant material application. Nonetheless, the volatility of potential breakthrough from advancements in technological accessibility makes the subject exciting to research in.

Fields such as cryptography, work in complexity theory for problems such as factoring and collision finding as well as their limiting factors in the NISQ era have been outlined extensively. From complexity theory, various frameworks for NISQ algorithm discussion have also been presented.

6. Conclusion

This paper has provided a comprehensive exploration of the burgeoning field of quantum complexity theory, particularly highlighting its relevance and application in the era of Noisy Intermediate-Scale Quantum (NISQ) devices. The discussion extended from the foundational principles laid out in classical computational complexity theory to the novel challenges and frameworks presented by quantum computing. By elucidating the relationship between traditional complexity classes and their quantum counterparts, notably BQP, this work has underscored the transformative potential of quantum algorithms such as Shor’s factoring algorithm and Grover’s search algorithm, demonstrating their profound implications for cryptography and database search, respectively. Looking ahead, the research landscape for quantum complexity theory is ripe with opportunities for significant breakthroughs and technological advancements. As the field continues to grapple with the inherent limitations of NISQ devices, including noise and error rates, the development of more sophisticated error correction techniques and the theoretical exploration of fault-tolerance are paramount. Future research will need to focus on refining these techniques to harness the full potential of quantum computing. Additionally, the exploration of hybrid quantum-classical algorithms offers a promising avenue for immediate practical applications, providing a bridge between current technological capabilities and the ideal quantum computing future.