Path Planning for Robots in Fire Scenarios based on Dijkstra Algorithm and Genetic Algorithm

Yingwei Song; Qihong Duan; Juntian Liu

doi:10.54254/2755-2721/2024.20625

1. Introduction

Fires pose a significant threat to the safety of people's lives and property. According to statistics from the National Interagency Fire Center (NIFC), there were 56,580 wildfires across the United States in 2023, burning 2.7 million acres of land [1]. As a result, the application of robots in firefighting has become a critical research area within the robotics industry. These robots not only enhance firefighting efficiency but also contribute to the safety of firefighters. This paper presents a method for optimizing and constructing a cost map using Genetic Algorithm (GA) and Dijkstra Algorithm under known fire conditions. Comparative verification demonstrates the superiority, feasibility, and versatility of this approach[2].

2. METHODS AND METHODOLOGY

2.1. Definition of fire environment

To mitigate the computational complexity, this paper implements the following simplifications for the fire scenario and the robot:

The fire environment map only includes height of obstacle, surface roughness, and fire sources.
The robotic system is endowed with the capability to ascend obstacles of a certain height. However, it exhibits varying velocities when traversing surfaces of different roughness and ascending obstacles of varying heights.
A 2.5-dimensional grid map is utilized to represent the fire environment, concurrently mapping the robot as a singular point within the map.

For instance: The value of $$map(x,y).h$$ represents the height of obstacle in $$cell(x,y)$$ ; the value of $$map(x,y).temp$$ represent the temperature of $$cell(x,y)$$ and the value of $$map(x,y).r$$ represent the roughness of $$celll(x,y)$$ . Considering the robot exhibits different velocities when ascending the edge of an obstacle and moving along the surface of the same obstacle, despite the identical elevation values at these times, this paper use the variance of height within the grid map to represent terrain fluctuations. Let denote the height at position in the height map. The local mean and local variance can then be calculated as follows:

2.1.1. Local Mean

\begin{equation} \mu(x,y)=\frac{1}{4}\sum_{i=0}^{1}\sum_{j=0}^{1}map(x+i,y+j).h \end{equation}

Where, $\mu(x, y)$ represents the average of the height value at position $$(x,y)$$ and all the height values within its $2 \times 2$ neighborhood.

2.1.2. Local Mean of Squared Heights

\begin{equation} E\Big[map^2(x,y).h\Big]=\frac{1}{4}\sum_{i=0}^{1}\sum_{j=0}^{1}map^2(x+i,y+j).h \end{equation}

Where, $E\Big[h^2(x,y)\Big]$ denotes the average of the squared height values at position $$(x,y)$$ and within its $2 \times 2$ neighborhood.

2.1.3. Local Variance

\begin{equation} \sigma^2(x,y)=E\Big[map^2(x,y).h\Big]-\mu^2(x,y) \end{equation}

Where, $\sigma^2(x,y)$ represents the local variance of the height values at position $$(x, y)$$ . It is obtained by calculating the difference between the mean of the squared heights and the square of the local mean. For better readability of mathematical symbols, in the following text, we will use $h_{var}(x, y)$ to represent $\sigma^2(x, y)$ . The physical significance of $h_{var}(x, y)$ is the degree of height variation at $$cell (x, y)$$ .

2.2. Construction of costmap

In the pursuit of facilitating our research within the relatively straightforward MATLAB environment and to diminish the computational time required to attain accurate experimental outcomes, this paper innovatively introduces the variable $$time$$ , which signifies the duration the robot expends traversing each cell within the map.

\begin{equation} time(x,y)=\alpha\cdot\frac{map(x,y).r}{v_{f}}+\beta\cdot\frac{1+h_{var}(x, y)}{v_{h}} \end{equation}

Where, $$vf$$ denotes the robot's velocity performance on surfaces with varying degrees of roughness, while $$vh$$ signifies the robot's velocity performance when ascending obstacles of differing heights. The coefficients $\alpha$ and $\beta$ serve as weights that can be manually adjusted through simulation experiments. By manipulating the robot's traversal over surfaces with diverse roughness levels and its ascent of obstacles with varying heights, and subsequently measuring the requisite time, these values can be estimated through an analysis of the simulation data. Following manual simulation experiments, this paper has derived the specific values for the parameters $\alpha$ , $\beta$ , $$v_f$$ , and $$v_h$$ , which are 1, 4, 1, and 1, respectively. Consequently, the expression for $$time$$ is as follows:

\begin{equation} time(x,y)=map(x,y).r+4\cdot(1+h_{var}(x, y)) \end{equation}

Ultimately, within the costmap, the cost value of each cell can be succinctly defined by the following formulation:

\begin{equation} cost(x,y)=w_{1}\cdot time(x,y)+w_{2}\cdot map(x,y).temp \end{equation}

Where, $$w1$$ and $$w2$$ symbolize the relative significance of time and temperature, respectively, on the costmap's cost value. These weights can be optimized through the Genetic Algorithm (GA) to be discussed later, which aims to achieve an optimal balance between the effects of time and temperature on the costmap. This optimization process is designed to assist the robot in planning a path that not only minimizes the time taken from the starting point to the destination but also maximally reduces the thermal exposure experienced by the robot during the traversal.

2.3. Dijkstra algorithm for path planning

The Dijkstra algorithm is a greedy algorithm used to solve the single-source shortest path problem. It is capable of finding the shortest path from a starting node to all other nodes in a graph[3]. The main principle of the algorithm is to maintain a set of unprocessed nodes and gradually expand the known shortest paths until the shortest path to the target node is found[4]. After obtaining the cost map, we use the Dijkstra algorithm to find the optimal path. Compared to common used algorithms like PRM, this algorithm returns a concrete result which is good for optimization. The pseudo code is shown in followings[5]: \caption{Dijkstra's Algorithm} \begin{algorithmic}[1] \REQUIRE Graph, source \ENSURE path, distance[target] \FOR{each node in Graph} \STATE distance[node] $\gets \infty$ \STATE previous[node] $\gets$ UNDEFINED \ENDFOR \STATE distance[source] $\gets 0$ \STATE priority\_queue $\gets \{source\}$ \WHILE{priority\_queue is not empty} \STATE current\_node $\gets$ node with smallest distance \IF{distance[current\_node] = $\infty$ } \STATE break \ENDIF \FOR{each neighbor of current\_node} \STATE new\_distance $\gets$ distance[current\_node] + edge\_weight(current\_node, neighbor) \IF{new\_distance $\lt$ distance[neighbor]} \STATE distance[neighbor] $\gets$ new\_distance \STATE previous[neighbor] $\gets$ current\_node \STATE priority\_queue.add(neighbor) \ENDIF \ENDFOR \STATE priority\_queue.remove(current\_node) \ENDWHILE \STATE path $\gets$ [ ] \STATE current\_node $\gets$ target \WHILE{previous[current\_node] is defined} \STATE path.prepend(current\_node) \STATE current\_node $\gets$ previous[current\_node] \ENDWHILE \RETURN path, distance[target] \end{algorithmic}

2.4. D.Application of Genetic Algorithm (GA)

The Genetic Algorithm (GA) is a search algorithm that simulates the principles of natural selection and genetics to solve optimization and search problems[6,7]. The alternative or potential solutions can be improved by GA through a process could mimicking biological evolution, which, in particular, includes inheritance, mutation, selection, crossover and so on. GA performs a global search across the entire solution space rather than being confined to local regions, and it can evaluate the fitness of multiple individuals in parallel, which facilitates the discovery of a global optimum or near-optimal solution[8]. The fitness function plays a crucial role in GA, serving as the metric for evaluating the quality of individuals (chromosomes), thereby determining the direction of the search and the effectiveness of optimization[9,10]. In this project, we define the fitness function based on the cost map and the optimal path as follows: We calculate the optimal path P from the starting point to the endpoint using the Dijkstra algorithm. The path consists of a series of coordinate points (ri, ci):

\begin{equation} P=\{(r_1,c_1),(r_2,c_2),...,(r_n,c_n)\} \end{equation}

The fitness value is calculated along the path $$P$$ as the sum of the temperature and time values at each point, As shown in the following formula:

\begin{equation} fitness=\sum_{i=1}^{n}\bigl[\lambda_{1}\cdot map(r_{i},c_{i}).temp+\lambda_{2}\cdot time(r_{i},c_{i})\bigr] \end{equation}

Where, $\lambda_{1}$ and $\lambda_{2}$ are weight coefficients. Considering the difference in the order of magnitude of time and temperature in the above formula, this paper sets the values to $$1$$ and $$9$$ respectively[11].

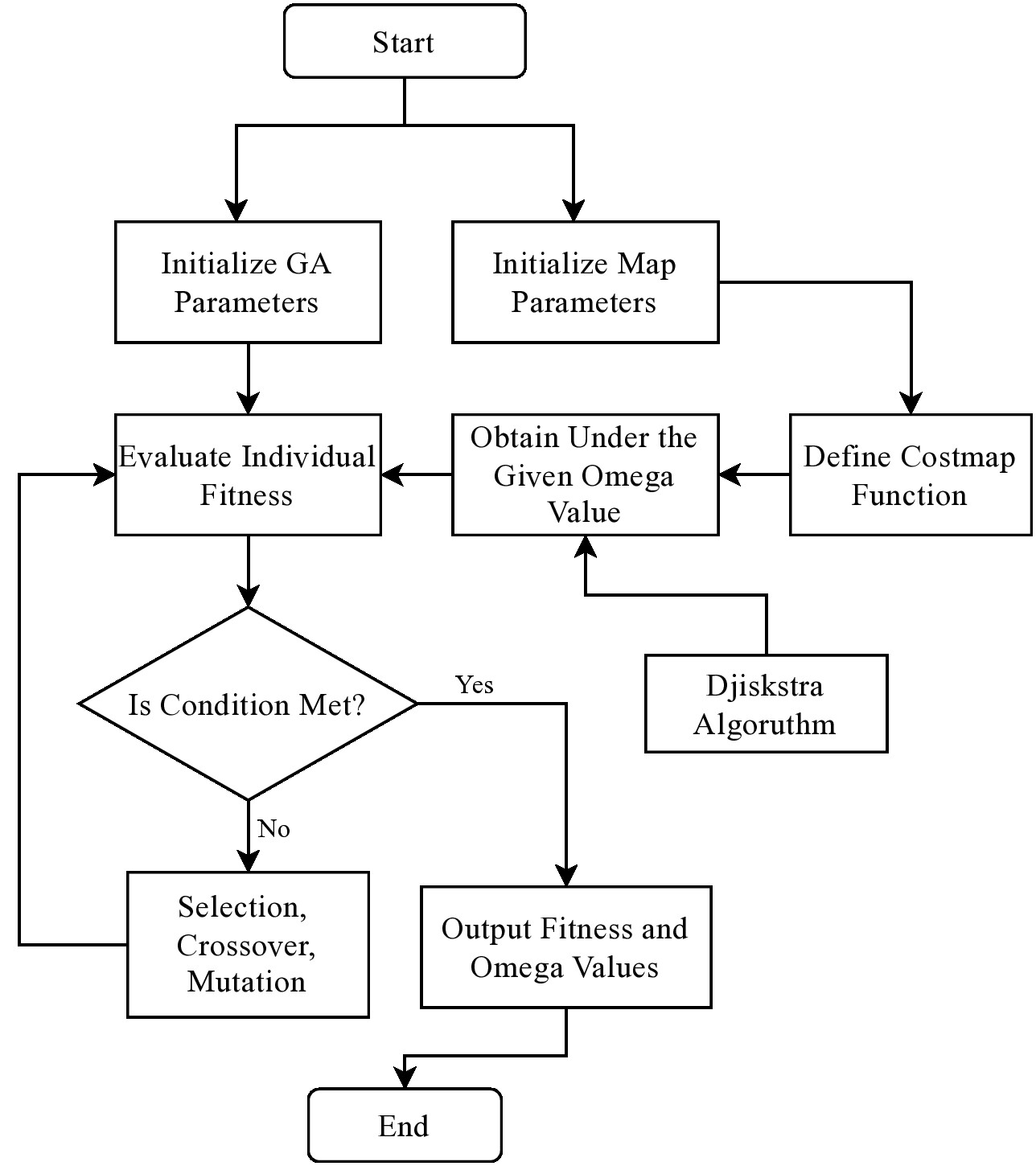
As shown in the Figure 1 , we visualize the genetic algorithm using a flowchart.

3. Result

To clearly demonstrate the advantages of applying GA and the rationality of the cost map definition, we compare the results under three different scenarios:

Case 1: Cost map defined solely based on roughness and height variance, without GA optimization.
Case 2: Cost map established based on temperature, roughness and height variance, w1 and w2 initialized to 1, without GA optimization.
Case 3: Cost map established based on temperature, roughness, and height variance, with GA optimization.

Using MATLAB to simulate these three scenarios, we obtain different outcomes: Initially, MATLAB was utilized to generate visual representations of the map's roughness, temperature, and elevation, as depicted in Figures 2, 3, and 4, respectively.

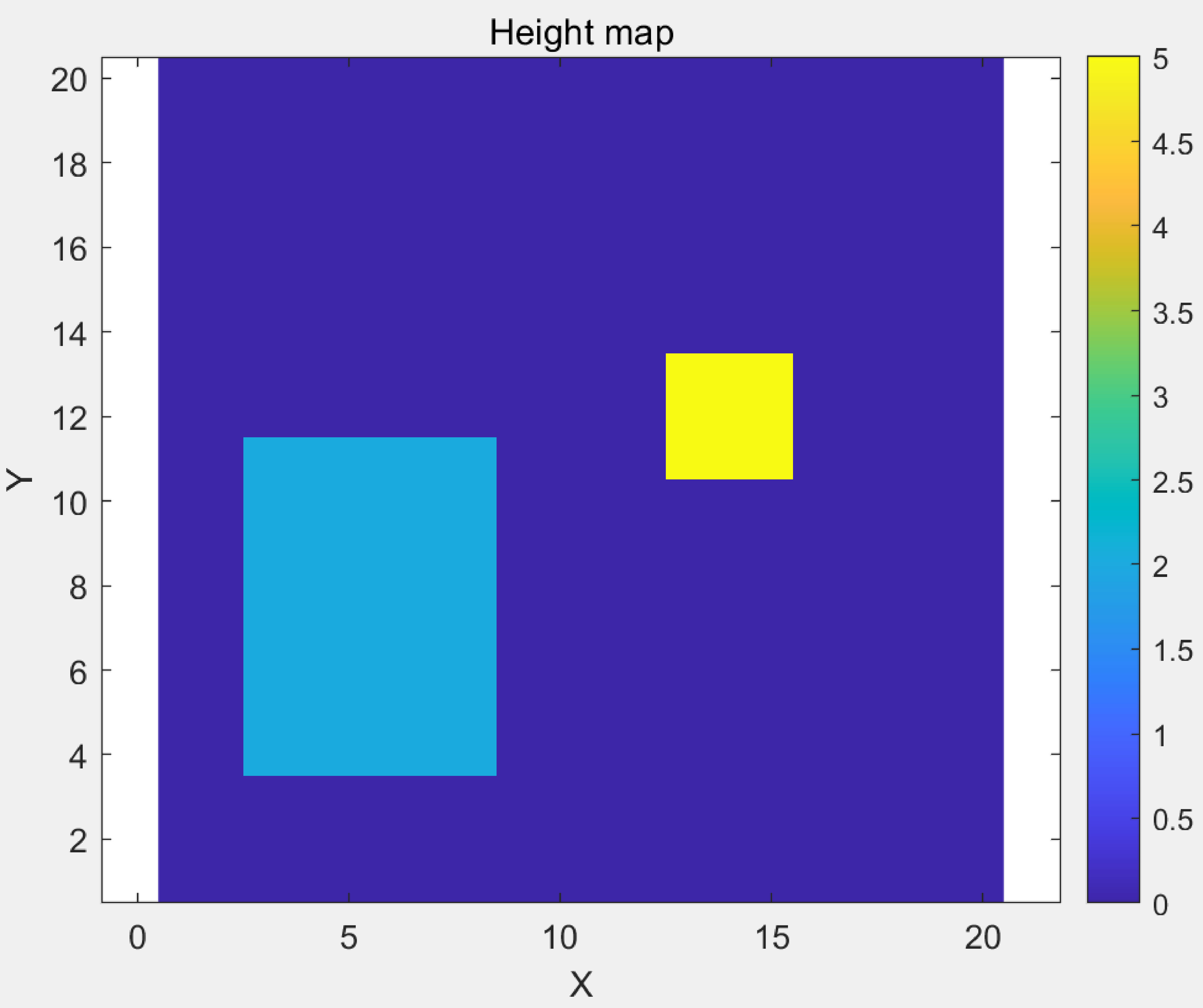
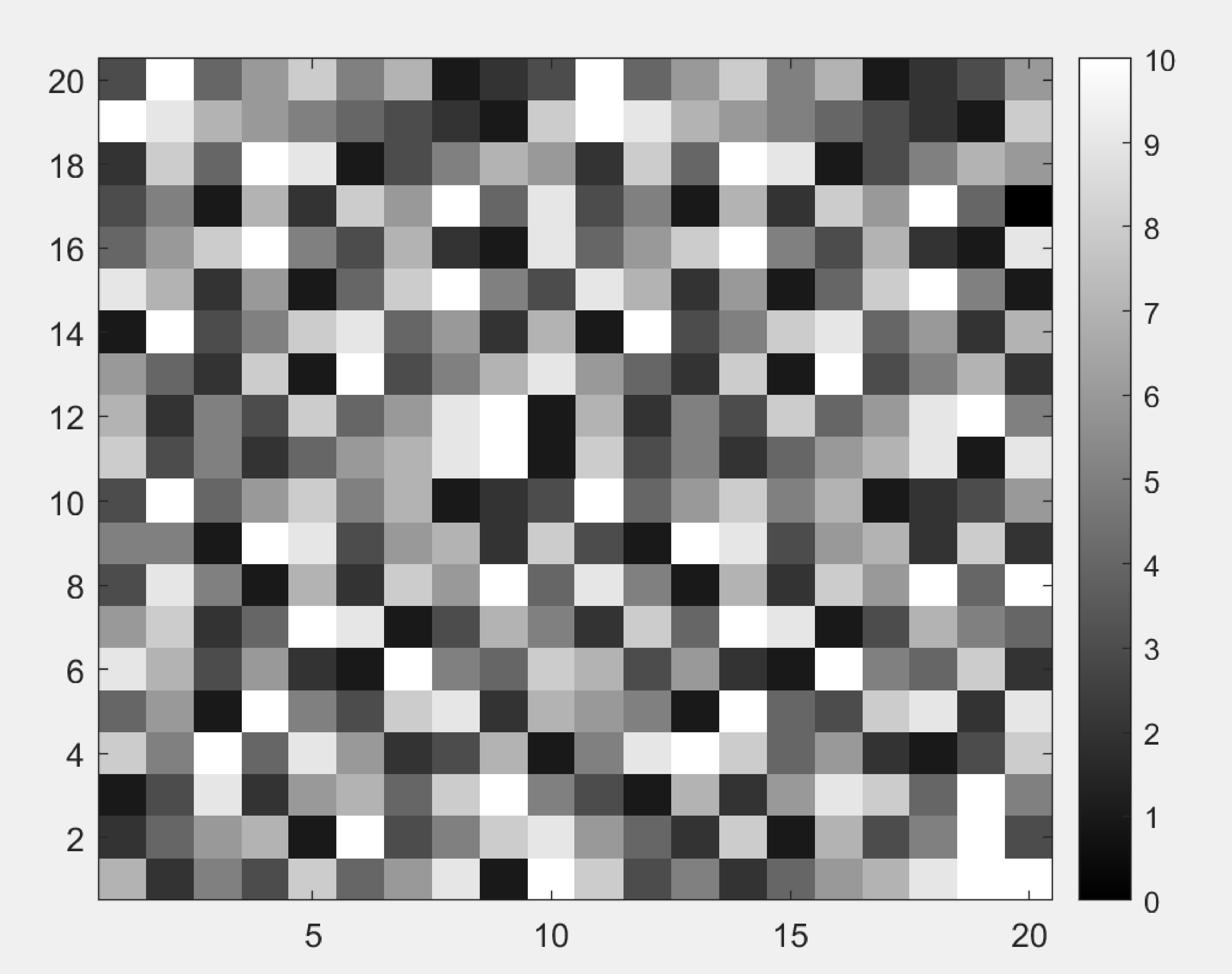
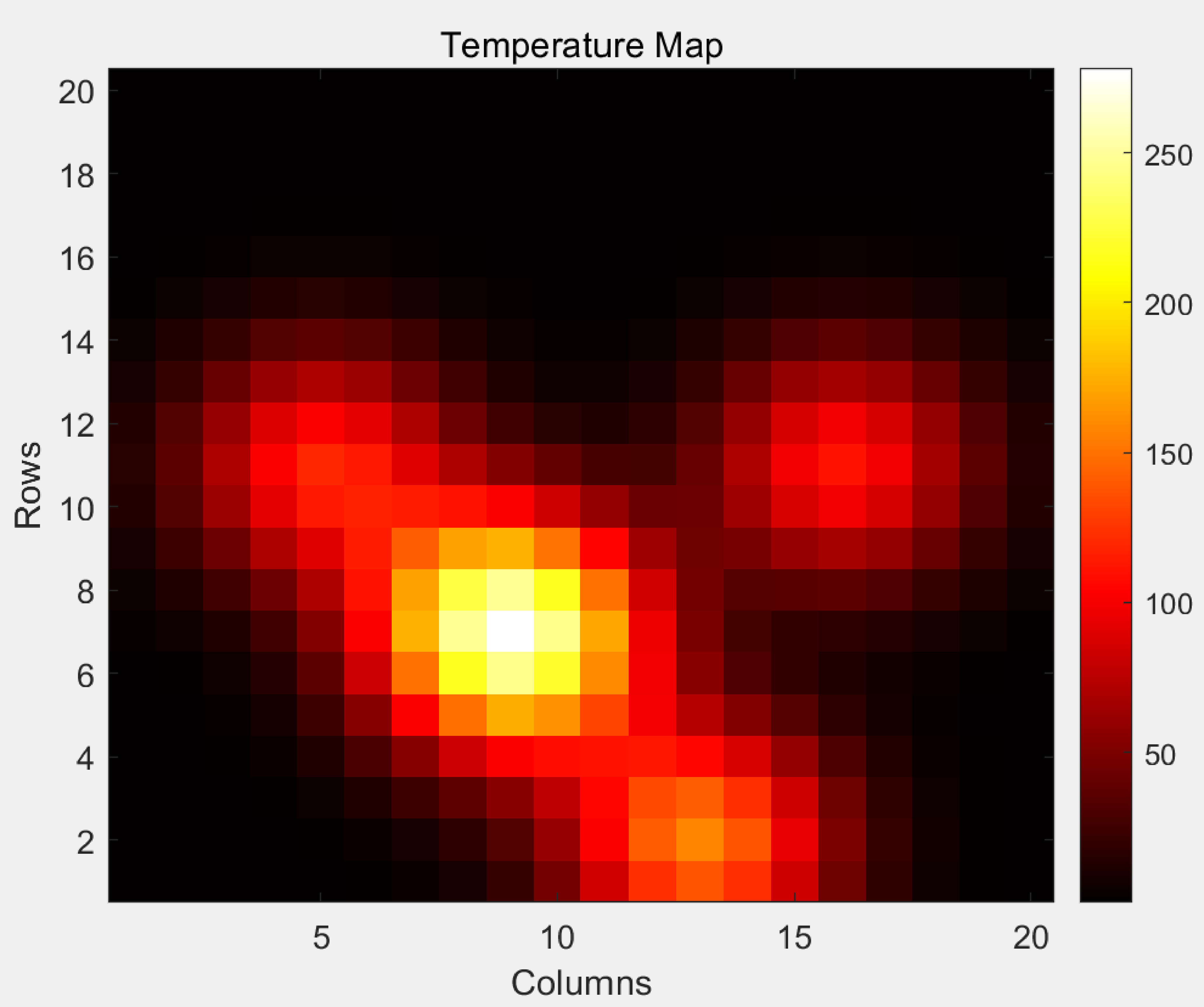
Finally, three distinct paths corresponding to different costmaps are revealed in Figures 5, 6, and 7, as the executing result of case 1, 2, and 3. By integrating the visual maps to observe the characteristics of the paths, it can be discerned that in case 1 (Figure 5), the robot considered only the height variance, resulting in a path with the minimum total time. However, this path directly traverses the high-temperature center, which is not the desired outcome in a fire scene; in case 2 (Figure 6), since the Genetic Algorithm (GA) was not employed to optimize the weights $\omega_1$ and $\omega_2$ in the cost value, the constructed costmap closely resembles the temperature map, largely neglecting the impact of height variance. Consequently, the path planned by the robot completely circumvents the high-temperature area, leading to a significantly increased time along the entire path, which is also not the desired outcome; in case 3 (Figure 7), with the optimization by the GA, it is evident that the constructed costmap effectively integrates the influence of height variance and temperature on the cost value. The planned path avoids the high-temperature areas and crosses the obstacles with low height values at the same time. This not only significantly reduces the cumulative temperature exposure along the entire path for the robot but also substantially shortens the time required to complete the total path.

By examining a table (Table [???]), the variance in the final value (hereinafter denoted as 'fval') for the robot upon completion of the paths corresponding to the three distinct cases becomes more apparent. It is evident that the fval for case 3 is markedly less than that of case 2, and the fval for case 2 is also less than that of case 1. This observation directly substantiates the viability and rationality of the approach we have proposed within the context of a simplified fire environment scenario. Specifically, it demonstrates the capability of the method to enable the robot to circumvent the high-temperature central zone while concurrently reducing the overall time required to traverse the designated path to the greatest extent possible.

Table 1: Final value of Case1,2,3

	Case 1	Case 2	Case 3
fval	2306.33	2281.98	2042.69

4. CONCLUSION

This project raises a method to construct the cost map based ib a grid map incorporating height, roughness, and fire sources, and optimized it using a Genetic Algorithm (GA). By analyzing and calculating the variance in terrain height and the impact of temperature, we effectively planned an optimal path for the quadruped robot within a simulated fire environment[12]. Our projects verified the effectiveness of combining height and heat based cost map and GA algorithm successfully, specifically in fire environment. This lays a solid foundation for future research and practical applications.

5. DISCUSSION

The improving points of our paper are the lack of simulation and map information.To the first point, basic ROS simulation has been achieved, which is able to calculate the path based on given algorithm, follow given way points and record the time from the start to the end[13]. The full simulation can show in the following paper. To the second point, more featured maps are being built to improve the effectiveness of the GA algorithm[14]. To deply our algorithm on the robot, we use simulink and ROS to simulate the running situation and test our algorithm efficiency on different map, as shown in figure 8, 9.

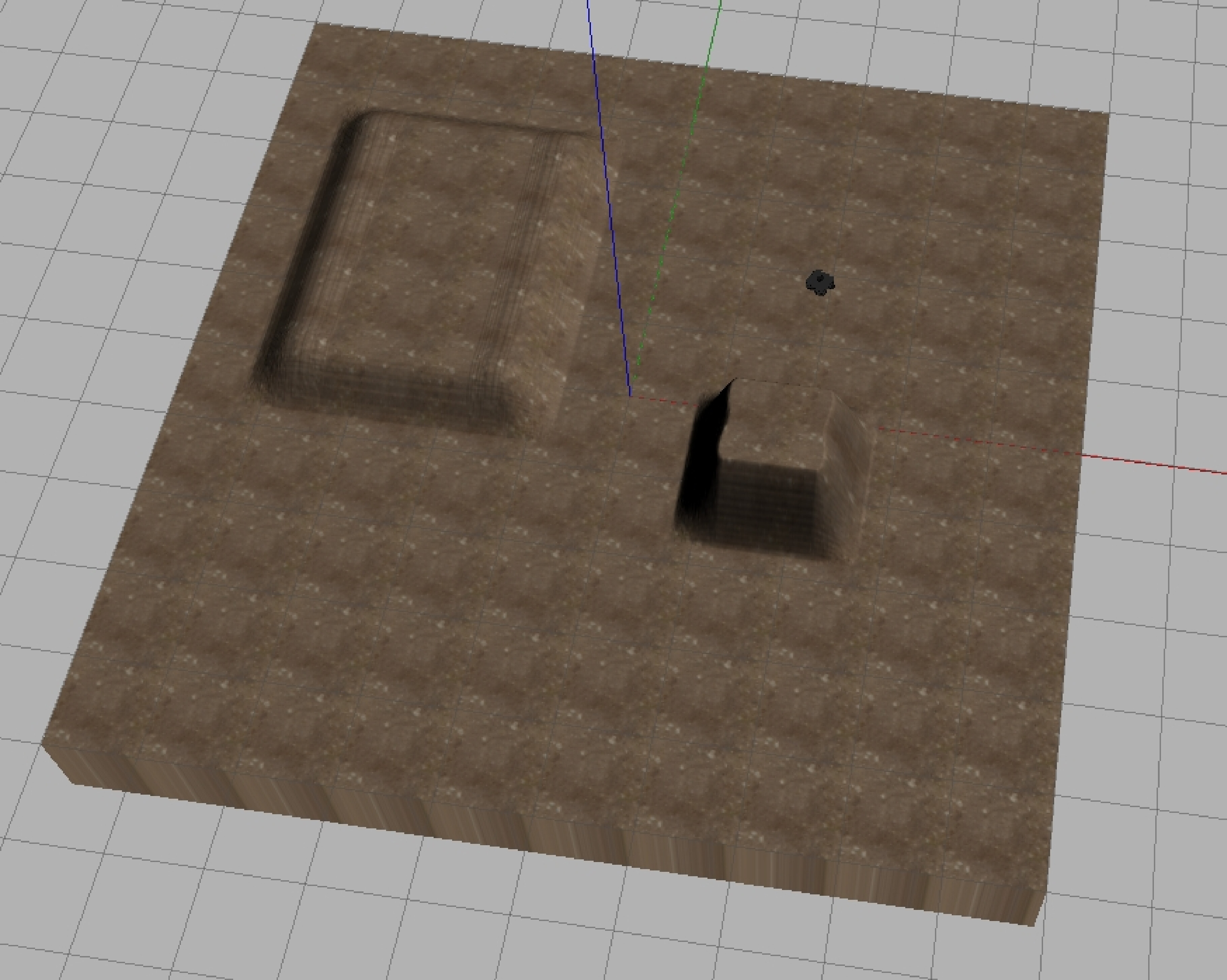
However, we get in trouble with combing ROS and GA algorithm in simulink. Therefore, we decide to rewrite our program in python code, so that we can do GA based on ROS-simulation time.

Acknowledgment

Yingwei Song and Qihong Duan contributed equally to this work and should be considered co-first authors. We would like to express our sincere gratitude to Neoschool for bringing together individuals from all corners of the world. Special thanks go to Professor Quan and the Teaching Assistants for their tireless guidance and instruction.

References

[1]. G. M. Kruijff, et al.: “Rescue Robots at Earthquake-Hit Mirandola, Italy: A field report,” Proc. of the 10th IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR2012), pp.1–8, 2012.

[2]. Bogue, R. (2021), ”The role of robots in firefighting”, Industrial Robot, Vol. 48 No. 2, pp. 174-178. https://doi.org/10.1108/IR-10-2020-0222

[3]. Ruinan Chen, Jie Hu et al. “An RRT-Dijkstra-Based Path Planning Strategy for Autonomous Vehicles.” Applied Sciences (2022). Ruinan Chen; Jie Hu; Wencai Xu.

[4]. DongKai Fan and Ping Shi. “Improvement of Dijkstra’s algorithm and its application in route planning.” 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery (2010). 1901-1904.. DongKai Fan; Ping Shi.

[5]. Alican Bozyigit, Gazihan Alankus et al. “Public transport route planning: Modified dijkstra’s algorithm.” 2017 International Conference on Computer Science and Engineering (UBMK) (2017). 502-505.. Alican Bozyigit; Gazihan Alankus; E. Nasiboglu.˘

[6]. W. Dougherty and R. D. Blanton. “Using regression analysis for GA-based ATPG parameter optimization.” Proceedings International Conference on Computer Design. VLSI in Computers and Processors (Cat. No.98CB36273) (1998). 516521.. W. Dougherty; R. D. Blanton.

[7]. Wenrui Zhao and Borui Wu. “Improved GA and Its Application in Performance Optimization of Electronic Components.” Advances in Multimedia (2022).. Wenrui Zhao; Borui Wu.

[8]. R. Ngamtawee and P. Wardkein. “Simplified Genetic Algorithm: Simplify and Improve RGA for Parameter Optimizations.” (2014). 55-64.. R. Ngamtawee; P. Wardkein.

[9]. V. Cicirello and Stephen F. Smith. “Modeling GA Performance for Control Parameter Optimization.” Annual Conference on Genetic and Evolutionary Computation (2000).. V. Cicirello; Stephen F. Smith.

[10]. Lim Wei Jer, Gerald Lee Jun Xiong et al. “GA-based Optimization for Circuit Design Assistance.” 2012 Third International Conference on Intelligent Systems Modelling and Simulation (2012). 732-736.. Lim Wei Jer; Gerald Lee Jun Xiong; S. Neoh; Arjuna Marzuki.

[11]. N. Mohan and N. Kasabov. “Transductive modeling with GA parameter optimization.” Proceedings. 2005 IEEE International Joint Conference on Neural Networks, 2005. (2005). 839-844 vol. 2.. N. Mohan; N. Kasabov.

[12]. Nathan P. Koenig, A. Howard. “Design and use paradigms for Gazebo, an open-source multi-robot simulator.” IEEE/RJS International Conference on Intelligent Robots and Systems (2004).. Nathan P. Koenig; A. Howard.

[13]. David Whitney, Eric Rosen et al. “ROS Reality: A Virtual Reality Framework Using Consumer-Grade Hardware for ROSEnabled Robots.” IEEE/RJS International Conference on Intelligent Robots and Systems (2018). 1-9.. David Whitney; Eric Rosen; D. Ullman; Elizabeth Phillips; Stefanie Tellex.

[14]. Brian P. Gerkey, R. Vaughan et al. “The Player/Stage Project: Tools for Multi-Robot and Distributed Sensor Systems.” (2003).. Brian P. Gerkey; R. Vaughan; A. Howard.

Cite this article

Song,Y.;Duan,Q.;Liu,J. (2025). Path Planning for Robots in Fire Scenarios based on Dijkstra Algorithm and Genetic Algorithm. Applied and Computational Engineering,132,95-103.

Data availability

The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.

Disclaimer/Publisher's Note

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

About volume

Volume title: Proceedings of the 2nd International Conference on Machine Learning and Automation

ISBN：978-1-83558-941-0(Print) / 978-1-83558-942-7(Online)

Editor：Mustafa ISTANBULLU

Conference website: https://2024.confmla.org/

Conference date: 21 November 2024

Series: Applied and Computational Engineering

Volume number: Vol.132

ISSN：2755-2721(Print) / 2755-273X(Online)

© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license. Authors who publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See Open access policy for details).

References

[2]. Bogue, R. (2021), ”The role of robots in firefighting”, Industrial Robot, Vol. 48 No. 2, pp. 174-178. https://doi.org/10.1108/IR-10-2020-0222

[3]. Ruinan Chen, Jie Hu et al. “An RRT-Dijkstra-Based Path Planning Strategy for Autonomous Vehicles.” Applied Sciences (2022). Ruinan Chen; Jie Hu; Wencai Xu.

[7]. Wenrui Zhao and Borui Wu. “Improved GA and Its Application in Performance Optimization of Electronic Components.” Advances in Multimedia (2022).. Wenrui Zhao; Borui Wu.

[8]. R. Ngamtawee and P. Wardkein. “Simplified Genetic Algorithm: Simplify and Improve RGA for Parameter Optimizations.” (2014). 55-64.. R. Ngamtawee; P. Wardkein.

[14]. Brian P. Gerkey, R. Vaughan et al. “The Player/Stage Project: Tools for Multi-Robot and Distributed Sensor Systems.” (2003).. Brian P. Gerkey; R. Vaughan; A. Howard.