1. Introduction

The sudden growth of blockchain technologies, especially Ethereum and other cryptocurrencies, has realigned the face of the financial sector. While their nature of decentralization and anonymity allows transactions to be conducted seamlessly across borders, the same features attract criminal activities such as money laundering and fraud. Anti-money laundering efforts have thus become an important concern for governments, financial institutions, and the blockchain community. Machine learning has emerged as a key tool in tacking these challenges by analyzing complex transactional patterns and behaviors. For example, Ethereum records every transaction, including account-to-account transfers and interactions with smart contracts, thus creating a rich dataset for identifying anomalous activities and fraudulent behavior [1, 2].

Applications such as fraud detection in blockchain ecosystems, machine learning was able to provide solutions. Liu et al. developed a model that utilized the LGBM-based mode on Ethereum illicit transaction detection. It proves to be capable of handling large-scale data and classifying between normal and suspicious transactions accordingly [1]. In Nguyen et al., an AML system further expanded this with more advanced integrations between blockchain data and machine learning algorithms. Their model returned high precision in identifying suspicious accounts, which again proved the capabilities of scalable machine learning frameworks in combating financial crimes [2].

Based on these, Zhang et al. extended them into GTN2vec-a graph embedding technique that captured in-depth transactional relationships from within the Ethereum network. Using the transactions as representations within graphs, their method did marvels in the detection of money laundering activities, offering new ways of doing relational modeling in blockchain AML [3]. Lin and Wei went further to trace the flow of stolen assets in the Ethereum heists to show the pattern of how illicit funds are laundered. Their study puts weight on how necessary it is to understand transactional flows while developing targeted AML measures [4].

Recent breakthroughs in graph-based learning have opened new directions for AML detection. Smith and Lee focused on the helpfulness of machine learning in blockchain technologies, especially in integrating relational transaction data that would improve fraud detection and scalability [5]. Wang and Zhang proposed LaundroGraph, a self-supervised graph representation learning framework leveraging structural information of blockchain transactions. Their work focused on embedding techniques in graphs to improve the strength of the model in detecting malicious activities within a complex network [6]. Zhao and Li presented GraphALM, an active learning model, balancing computational efficiency with high accuracy. The model tackled challenges related to a large-scale transaction dataset coming from blockchain platforms [7].

Despite the progress made, several challenges persist in blockchain AML detection. One significant issue is the class imbalance problem, where fraudulent transactions account for only a small portion of the dataset. This imbalance makes it difficult for models to generalize effectively. To address this, Chen et al. applied traditional AML algorithms to blockchain scenarios, emphasizing the need for feature engineering tailored to the unique characteristics of Ethereum data [8]. Liu and Zhao further advanced this approach by incorporating oversampling techniques and adaptive learning to improve the performance of machine learning models in handling imbalanced datasets [9].

This research builds on existing work by comparing Logistic Regression, Random Forest, and XGBoost for Ethereum AML detection. Insights from Zhang et al. and Chen et al. guide the implementation of ensemble methods and oversampling strategies to address the persistent issue of class imbalance in blockchain data [10, 11]. Additionally, this study incorporates graph-based approaches inspired by recent advancements in LaundroGraph and GraphALM, utilizing the relational and structural information inherent in Ethereum transactions to improve detection accuracy and scalability [12, 13].

The structure of this paper is as follows: Section 2 describes the data gathering, data preprocessing, and machine learning models used. Section 3 describes the experimental design, model assessment metrics, and results. Section 4 discusses the findings; hence, the strengths of each model and their inability to assess some features. Section 5 concludes the main findings along with the limitations and ways for further research. This structure has helped the paper conduct a thorough review of Ethereum AML detection using machine learning methods that will give valuable insights to both academia and industry.

2. Data and Method

2.1. Data Collection and Description

The dataset used in this study was sourced from Kaggle’s publicly available Ethereum Anti-Money Laundering (AML) dataset, which contains multiple Ethereum accounts and their transaction features. After data cleaning, a total of 7,121 samples were retained. The legality of transactions was determined by the target variable FLAG, where FLAG=0 represents legitimate transactions and FLAG=1 denotes illegal transactions.

The original data exhibited a significant class imbalance: legitimate transactions (FLAG=0) accounted for 81.04% of the dataset, totaling 5,771 samples, while illegal transactions (FLAG=1) constituted 18.96%, with 1,350 samples (see Table 1).

Table 1: Description of Ethereum Account Transaction Features.

2.2. Data Pre-processing

The raw dataset contained missing values in some numerical features. To ensure data quality, these missing data points were removed. Additionally, the class distribution in the original dataset was highly imbalanced, with illegal transactions (`FLAG=1`) accounting for only 18.96%. This imbalance could lead to the model being biased toward the majority class (legitimate transactions).

To address this issue, an undersampling method was used to adjust the class distribution to a 60:40 ratio. Specifically, all minority class samples (`FLAG=1`, totaling 1,350 samples) were retained. From the majority class samples (`FLAG=0`), 2,025 samples were randomly selected and combined with the minority class samples. The resulting balanced dataset contained 3,375 samples. A comparison of the class distribution before and after adjustment is shown in Table 2.

Table 2: A Comparison of FLAG Class Distribution Before and After Adjustment.

All numerical features in the dataset were standardized using the StandardScaler to transform the feature values into a distribution with a mean of 0 and a standard deviation of 1. This standardization reduced the impact of varying scales among different features. The dataset was then split into training and testing sets using the train_test_split function, ensuring consistent distribution between the training and testing data.

2.3. Model Description

2.3.1. Logistic Regression

Logistic Regression is a classic linear classification model widely used in binary classification tasks. The model maps the output of linear regression to probabilities between [0, 1] using the Sigmoid function, and samples are classified based on a defined threshold. The core concept is to estimate the probability of the target variable using the linear relationship of log odds, as shown in Equation (1).

\( P(y=1|x)=\frac{1}{1+{e^{-({w^{T}}x+b)}}}\ \ \ \) (1)

Here, \( x \) represents the input feature vector, \( w \) is the weight vector indicating the importance of each feature, and \( b \) is the bias term that adjusts the overall probability of the model. Classification decisions are made by setting a threshold; for example, \( P(y=1|x)≥0.5 \) , the prediction is \( y=1 \) ; otherwise, \( y=0 \) . Logistic Regression estimates the parameters \( w \) and \( b \) by maximizing the log-likelihood function, improving the model’s ability to fit the target variable. In this study, the Logistic Regression model was configured with the parameter class_weight='balanced' to address the class imbalance, and the maximum number of iterations was set to 1,000 to ensure convergence during optimization.

2.3.2. Random Forest

Random Forest is an ensemble learning method based on decision trees. It enhances classification performance by constructing multiple random decision trees and combining their results through voting or averaging. The final classification result of Random Forest is determined by the majority vote of all decision trees, as expressed in Equation (2):

\( \hat{y}=Mode\lbrace {T_{1}}(x),{T_{2}}(x),…,{T_{n}}(x)\rbrace \) (2)

Here, \( ({T_{i}}(x)) \) is the prediction of the i-th tree for sample x. There are n decision trees in total. Random Forest uses bootstrap sampling to randomly select several samples from the original dataset to construct each tree. Besides, in each split, Random Forest also randomly selects a subset of features to increase its diversity and improve generalization.

In this problem, 100 trees were configured for the Random Forest, and then the parameter class_weight='balanced' was passed to tackle class imbalance. Also, for the performance evaluation of models, the cross-validation technique should be adapted to ensure good learning of the model across different samples.

2.3.3. eXtreme Gradient Boosting

eXtreme Gradient Boosting(XGBoost) is a gradient boosting-based ensemble learning algorithm, which has the best characteristics of efficient training performance and powerful nonlinear modeling. Constructing multiple weighted decision trees and iteratively optimizing the prediction error improve the generalization capability of the model's classification. The prediction result in Equation (3) is determined as the weighted sum of all the weak learners.

\( \hat{y}=\sum _{t=1}^{T}{f_{t}}(x),{f_{t}}∈F \) (3)

Here, \( {f_{t}}(x) \) denotes the prediction of the t-th tree for input sample x and \( F \) is the function space of all regression trees. The model is optimized through minimization of the objective function defined in Equation (4).

\( L=\sum _{i=1}^{n}l({y_{i}},\hat{y_{i}^{(t)}})+\sum _{t=1}^{T}Ω({f_{t}})  \) (4)

In this equation, \( l \) represents the loss function (e.g., logarithmic loss), and \( Ω({f_{t}}) \) is the regularization term used to control model complexity and reduce the risk of overfitting. XGBoost introduces several unique features, including regularization for improved generalization, support for parallel computing to accelerate training, and the ability to analyze feature importance. These characteristics make it highly effective for handling high-dimensional data and complex nonlinear relationships.

In this study, the XGBoost model was configured with the parameter scale_pos_weight=10 to address class imbalance. The evaluation metric eval_metric='logloss' was used, and the learning rate was set to 0.1 to optimize the model’s sensitivity to imbalanced data.

3. Results and Discussion

3.1. Experimental Setup

Below is the code that split the dataset into 80% training data and 20% testing data. StandardScaler was used to standardize all feature variables in order not to get the impact of different scales among features while training models. To evaluate different models, three classification algorithms commonly used are selected: Random Forest, XGBoost, and Logistic Regression.

It was evaluated by two metrics-ROC AUC, being the metric used for this problem that is going to tell about the ability of the model in classifying between a genuine and fraud transaction; Accuracy is about general model performance on the test set. Further assurance on model stability and generalization-Stratified K-Fold Cross Validation during training was necessary in order for performances to be consistently reproduced given small subsets.

3.2. Experimental Results in Tables and Graphs

This section presents the main experimental results, along with intuitive comparisons through tables and figures.

Table 3: Model Performance Comparison

The accuracy of XGBoost from Table 3 is the highest at 98.52%, followed by Random Forest at 97.63%. While XGBoost presented the best accuracy, Random Forest presented a slightly higher ROC AUC, which means it was better in terms of the discrimination ability between positive and negative samples. Logistic Regression, given its linear assumptions, demonstrated much weaker performance compared to the other models.

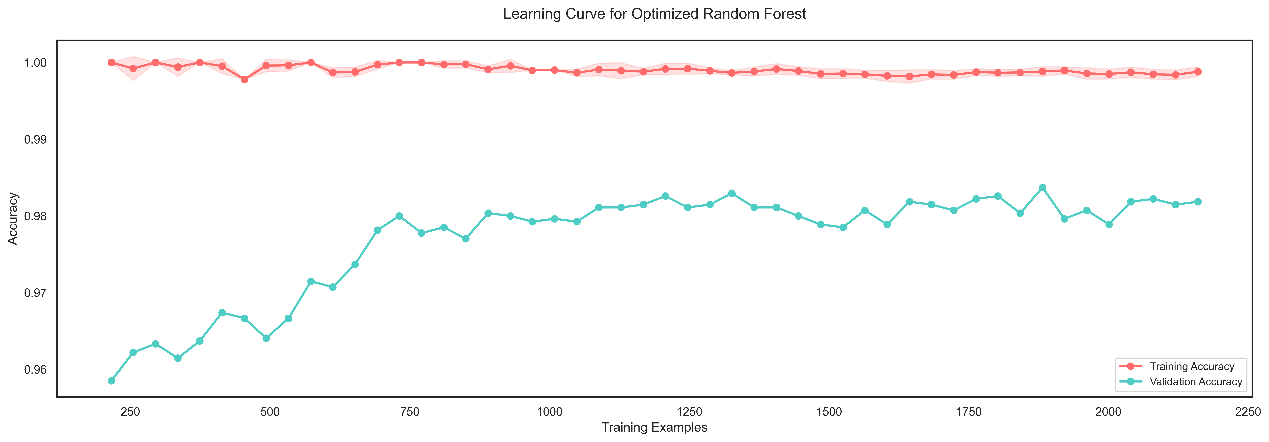
Figure 1: Learning Curve of Optimized Random Forest Model. (Picture credit: Original).

The performance of the Random Forest model was further fine-tuned: by increasing the number of trees, restraining the depth of trees, tuning the minimum number of samples required to split, also on leaf nodes, and performing class balancing. Figure 1 depicts a clear representation using a learning curve about the model improvement.

Also, the best Random Forest model was very good, with an accuracy on test data of 97.63%, compared with 98.52% for XGBoost, though it outperformed XGBoost regarding AUC-ROC, which means a greater effectiveness in distinguishing between positive and negative samples. With regard to Logistic Regression, Random Forest expressed better nonlinear relationships inherent in the data and was more impressive.

XGBoost gives the best performance, but Random Forest is far more stable regarding the computational efficiency and feature complexity and, therefore, applicable for large-scale data processing. Logistic Regression works well in the case of a simple problem and when linearity can be assumed; this was not the case here, hence its performance was not very good, since it cannot model nonlinear relationships.

It follows from the outcomes that though XGBoost is the most accurate model, Random Forest presents a possible alternative for efficient handling of imbalanced data and complex features and, therefore, is useful for scalable applications.

4. Conclusion

This paper compared the performance of various machine learning models for classification into either legitimate or fraudulent transaction classes using the Ethereum AML dataset.

Among these, the result comparison of Logistic Regression, Random Forest, and XGBoost shows that XGBoost possesses the highest accuracy of 98.52%, while the Random Forest is slightly better in terms of distinguishing between positive and negative samples. By contrast, logistic regression always shows inferior performance in dealing with complex features because of the restriction of the linear assumption. Standardization of data, undersampling, and tuning parameters have been done to deal with class imbalance. The results proved that ensemble methods are still a better choice for financial transaction classification tasks.

However, the only limiting factors are that this paper is based on a single dataset and has not considered the temporal dynamics of features, which may affect the generalization capability of results and their adaptability to real-time fraud detection.

Follow-up research can add more data from diverse sources and dynamics, and hybrid models might be further tried to develop the current performance. It offers new practical directions for anti-money laundering methods applied on blockchain transaction data, with great theoretical value and practical importance.