1. Introduction

The Proportional-Integral-Derivative (PID) controller has long dominated industrial control systems due to its simple structure, good stability, and ease of implementation. However, with the increasing complexity of industrial control, traditional PID control methods face more challenges. In particular, in dynamic and nonlinear systems, the fixed parameters of the PID controller are unable to adapt to new environments, causing response delays and high sensitivity to external disturbances. These problems limit the applicability of PID controllers in modern, complex control tasks. In recent years, various improvement methods like optimization algorithms, adaptive control, and machine learning strategies, have been proposed to address the limitations of traditional PID control. However, many studies focus on one method or strategy and are often confined to specific experimental conditions, lacking a comprehensive evaluation of different optimization strategies. Thus, the paper reviews the existing literature, examining the basic principles of PID controllers, parameter tuning methods, and recently proposed optimization strategies. Specifically, this paper provides a detailed analysis of the research advancements in modern improvement methods, such as optimization algorithms, adaptive control, and machine learning, evaluates the effectiveness of these methods in practical applications, and discusses how they address the major challenges faced by traditional PID control, including difficulties in parameter adjustment, response delays, and sensitivity to disturbances. This review aims to provide theoretical support for the further development of PID control technology and offer guidance for researchers and engineers in related fields.

2. Overview of traditional PID controllers

2.1. Basic components of the PID controller

The PID controller is one of the most widely used control algorithms in industrial applications due to its simple structure, ease of implementation, and strong robustness and stability, which make it a popular choice among engineers. The theory behind the PID controller was originally proposed by Maxwell in 1868 [1], laying the foundation for its widespread use in control systems.It adjusts the control signal based on three error components: proportional (P), integral (I), and derivative (D), each contributing to the system response. These components optimize the dynamic performance of the system by adjusting their gain values to meet specific criteria, such as overshoot and settling time. The basic structure of the PID controller is shown in Figure 1.

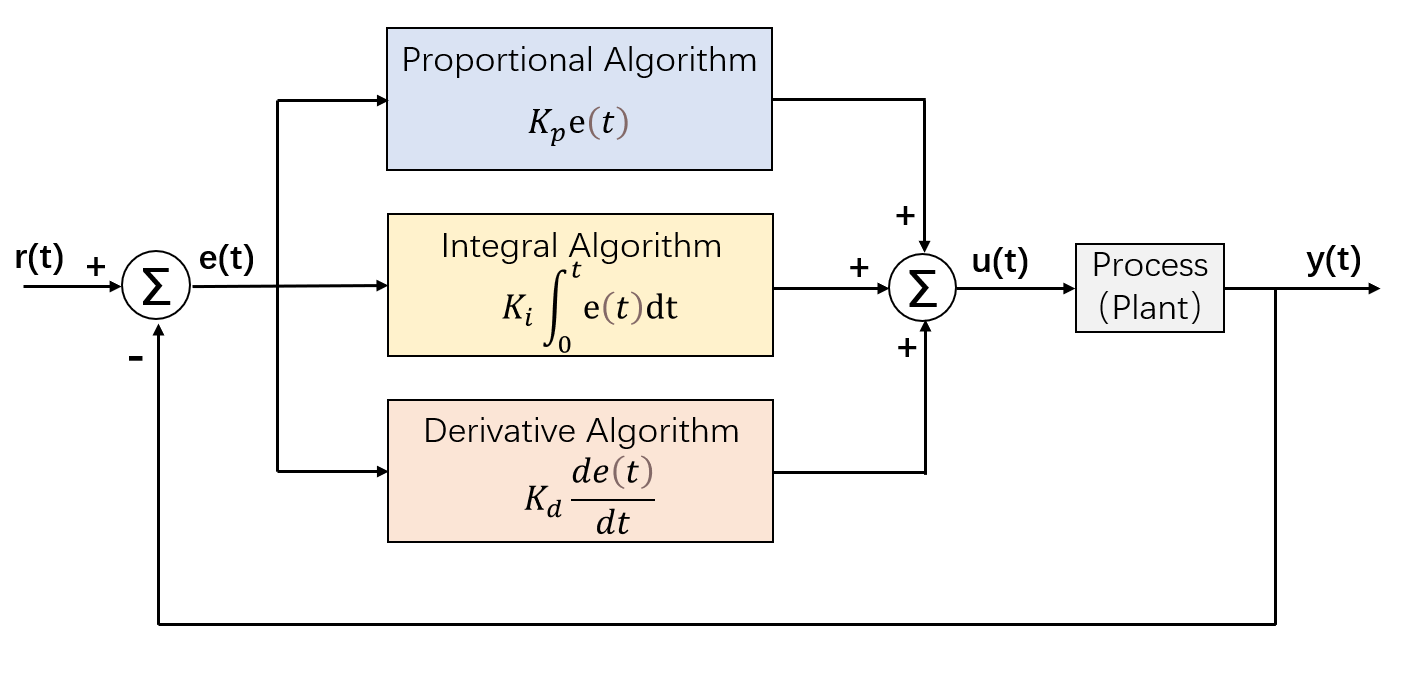
Figure 1: Basic structure of the PID controlle

The PID controller processes the system’s error signal through three components: proportional, integral, and derivative, to generate the control input, driving the system output to gradually reach the desired target value. The system error \( e(t) \) is determined by the difference between the input value \( r(t) \) and the output value \( y(t) \) . The general form of the PID controller rule is expressed as:

\( u(t)={K_{p}}e(t)+{K_{i}}\int _{0}^{t}e(τ)dτ+{K_{d}}\frac{de(t)}{dt} \) (1)

\( ⅇ(t)=r(t)-y(t) \)

where \( {K_{p}} \) is the proportional gain, which adjusts the system’s response speed and is a key factor in the PID controller’s performance. A high \( {K_{p}} \) can lead to increased system oscillations, negatively affecting stability, while a low \( {K_{p}} \) can lead to slow response times and excessive damping. \( {K_{i}} \) is the integral gain, which eliminates steady-state error and improves zero steady-state error performance. Although it adjusts the control output by accumulating the error values over time, ensuring the system output eventually reaches the target value, the integral action is slow and always lags behind changes in the error signal. \( {K_{d}} \) is the derivative gain, which helps counter the slow response of the integral action and maintains a faster system response, reduces overshoot, minimizes oscillations, and improves dynamic performance. However, if this value is too high, it may amplify system noise. These gain values must be adjusted based on the specific application and system characteristics, as different combinations of parameters directly impact the system’s performance. For instance, if the system exhibits a large steady-state error, it may be necessary to increase the integral gain \( {K_{i}} \) , while a large overshoot may require increasing the derivative gain \( {K_{d}} \) to improve the system's response characteristics.

2.2. Parameter tuning method

Traditional parameter tuning methods for PID controllers include the Ziegler-Nichols (ZN) and the Cohen-Coon (CC) methods. The ZN method relies on a closed-loop critical oscillation experiment. First, in the closed-loop control system, the integral (I) and derivative (D) actions are temporarily disabled, leaving only the proportional (P) control. Starting with a relatively low proportional gain \( {K_{p}} \) , the gain is gradually increased until the system output begins to exhibit continuous and stable oscillations. The gain at this point is called the critical gain \( {K_{u}} \) . When sustained oscillations occur in the system at \( {K_{p}}={K_{u}} \) , the time interval between two consecutive peaks (or troughs) is measured, which corresponds to the critical oscillation period \( {T_{u}} \) . The PID parameters can then be determined according to the ZN empirical formulas:

\( {K_{p}}=0.6{K_{u}} \) , \( {T_{i}}=0.5{T_{u}} \) , \( {{T_{d}}=0.125T_{u}} \) (2)

The CC method involves analyzing the process response curve to determine the system’s critical time constant \( {T_{c}} \) and the proportional bandwidth \( R \) . Using these parameters, the CC rule is applied to calculate the proportional, integral, and derivative gains.

The ZN method requires only a closed-loop experiment, gradually increasing the proportional gain to obtain \( {K_{u}} \) and \( {T_{u}} \) . It is suitable for situations where an accurate model is unavailable, but it requires the researcher to have extensive experience. This method often results in larger overshoot and oscillations due to tuning at the marginally stable state. In addition, the CC method is based on the step response curve. By identifying process gain, delay time, and time constant, this method represents the system’s dynamics well. For systems with delays, it typically offers smoother, more robust control, reducing overshoot. Based on the water level control system experimental platform, a closed-loop control system was built using Arduino and Matlab to compare the tuning effects of the ZN and CC methods, showing that after adding the Kalman filter, the CC-tuned PI controller has smoother rise and settling times, while the ZN-tuned PID controller responds faster [2].

2.3. Benefits and limitations of traditional PID

The traditional PID controller is widely used in many fields due to its simple structure and intuitive design. Since it relies solely on system error and its derivatives, the PID controller does not require complex mathematical modeling, making it easy to implement. This makes the PID controller well-suited for applications in fields like motion control, process control, power electronics, hydraulics, pneumatics, and manufacturing [3]. Its broad applicability and low implementation cost have kept the PID controller an essential tool in modern industrial applications like autonomous driving and drones [4]. For example, in the drone field, a nonlinear PID auto-tuning method based on deep reinforcement learning (PPO) enables seamless switching between manual and autonomous modes, improving flight control response and stability [5].

Despite its benefits like good real-time performance, stability, and cost-effectiveness, traditional PID controllers have certain limitations. Firstly, the PID parameters are fixed and difficult to adjust dynamically, making it unable to automatically adapt to changes in system parameters, leading to a decline in control accuracy. This is especially problematic when facing external disturbances, as the PID controller has limited adjustment capabilities, which challenges the requirements of high-precision control systems. Moreover, the derivative component (D) of the PID controller helps reduce overshoot and improve dynamic performance but is sensitive to high-frequency noise, which can amplify noise and cause instability. As the demand for precision and real-time performance grows in modern industries, the limitations of the traditional PID controller have become more apparent, making it inadequate for high-demand industrial control tasks. To meet more complex system requirements, recent research has focused on combining intelligent control algorithms with traditional PID controllers to optimize their performance.

3. Modern improvements of PID controllers

3.1. PID parameter optimization based on the MZOA algorithm

The Zebra Optimization Algorithm (ZOA) is a metaheuristic optimization algorithm based on zebra foraging and anti-predation behavior, characterized by few control parameters, simple structure, and ease of modification. However, ZOA tends to get stuck in local optima, converge slowly, and lacks strong global search capability, requiring improvements. Based on ZOA, a Multi-strategy Fusion-based Improved ZOA (MZOA) was proposed, enhancing PID optimization with chaotic mapping, tangent flight strategy, and SCA oscillation search, improving convergence, global search, and local search precision. Its performance was validated in a second-order lag system [6]. And the improved system outperforms the ZOA algorithm in parameter optimization, achieving faster convergence, as shown in Figure 1. The optimized PID parameters enhance system stability and control accuracy, reducing the settling time by 55.3%.

\( G(s)=\frac{{ⅇ^{-0.5s}}}{{s^{2}}+2s+1} \) (3)

Table 1: Comparison of the performance of MZOA and ZOA algorithms

MZOA is an improvement upon ZOA, enhancing its global search capability and avoiding local optima, boosting PID parameter optimization. The specific improvements include initializing the population by combining Tent chaotic mapping and Householder mirror reflection learning to avoid issues of individual repetition or aggregation caused by traditional initialization methods, thereby increasing population diversity. The use of tangent flight strategy for position updating strengthens global search capability, preventing local optima. Additionally, the introduction of a hyperbolic cosine enhancement factor improves the oscillation capability of the SCA, allowing better switching between local and global searches and enhancing the ability to escape local optima.

3.2. Adaptive PID control methods

Traditional PID controllers, due to the fixed parameters, cannot adapt to environmental changes like external disturbances and system nonlinearity. To address this issue, the Adaptive PID (APID) was introduced to automatically adjust PID parameters based on system dynamics, maintaining optimal performance. APID control methods have been widely researched and applied in various fields. For instance, in autonomous vehicle trajectory tracking, the vehicle needs to frequently change lanes, avoid obstacles, and stay in sync with traffic flow in complex urban environments [7]. Traditional PID struggles to maintain stable trajectory tracking when vehicle speed varies significantly, while APID adjusts control parameters in real-time, significantly reducing path errors and enabling high-precision tracking at different speeds and steering angles. Compared to traditional PID, trajectory error is reduced from 1m to 0.5m, greatly improving control accuracy.

However, conventional APID requires high computational resources for real-time adjustments, especially with optimization algorithms, making it challenging for high-real-time systems. As such, a novel APID controller, Seesaw APID, was proposed, boosting the adaptability of the traditional PID using the Seesaw Algorithm, and improving response speed and stability in dynamic systems [8]. It dynamically adjusts gain to reduce overshoot and oscillation. The core idea of this algorithm is to regulate the error derivative ( \( {m_{orig}}={e^{ \prime }}(t) \) ) to control the system’s dynamic characteristics, allowing it to converge more quickly or approach the setpoint more smoothly.

In comparison to conventional APID, Seesaw APID dynamically adjusts PID gains based on the calculation of both the error \( e(t) \) and its derivative \( {e^{ \prime }}(t) \) , enabling the controller to adapt to varying control demands. Moreover, two algorithms, MS Seesaw and LS Seesaw, were designed to enhance the effectiveness of the APID controller. The control effects of traditional PID, APID-MS, and APID-LS were compared using the typical transfer function \( G(s) \) and the IPC (Inverted Pendulum on a Cart) as test objects, with the results shown in Tables 2 and 3.

\( G(s)=\frac{1}{(s+2)(s+3)(s+4)} \) (3)

Table 2: Performance comparison for transfer function

Table 3: Performance comparison for IPC system

It can be seen that Seesaw APID reduces rise time by 9.6%, overshoot by 20.9%, and settling time by 68.2%, improving the overall performance of the control system. APID-MS accelerates convergence, reducing rise time and increasing gain when the error is large, enhancing control and stability. APID-LS reduces overshoot to improve stability, decreases settling time, and lowers gain when the error is small, reducing oscillation and making the system more stable. Both algorithms effectively boost the PID controller’s adaptability, allowing dynamic parameter adjustment without complex modeling or training. APID-MS (MS Seesaw APID) is suitable for improving response speed, while APID-LS (LS Seesaw APID) is better for enhancing system stability. Thus, Seesaw APID is an efficient, low-computation adaptive control solution for dynamic systems.

3.3. Integration of machine learning methods with PID

There is a marked overlap between the fields of control and machine learning in terms of objectives, problem statements, and tools. As such, many machine learning algorithms share similarities with classical control methods. The combination of control theory and machine learning algorithms is being explored to achieve optimization improvements. Machine learning techniques like random forests and SGD, can be used to determine optimal PID parameters, reducing the need for manual tuning. Additionally, the integration of the PID controller into deep learning optimization has led to the development of a PID-accelerated optimizer (PIDAO), which enhances the convergence speed and stability of gradient descent [9].

As a branch of machine learning, Q-Learning is a value iteration-based reinforcement learning algorithm. It is a model-free learning method that enables an agent to learn optimal policies through trial and error by interacting with a dynamic environment. In robotic control, while Q-Learning can determine optimal motion paths, it lacks fine-grained control over robot dynamics. Thus, combining the PID algorithm with the Q-Learning algorithm allows the PID controller to fine-tune the motion, ensuring that the robot accurately follows the path calculated by Q-Learning. Prior study explored how to combine Q-Learning with the traditional PID controller to optimize the trajectory tracking capability of mobile robots in unknown environments, demonstrating that the combined method of Q-Learning and PID outperforms the use of Q-Learning alone or traditional fuzzy control in terms of trajectory tracking, speed, and stability [10].

Table 4: Trajectory tracking experiment results

Table 5: Velocity and stability experiment results

As shown in Tables 4 and 5, the Q-Learning + PID combination outperforms using Q-Learning alone. The robot movement is smoother, obstacle avoidance ability is improved, with an average trajectory error reduced by 44.2% and navigation time shortened by 21.1%.

Furthermore, machine learning methods have been utilized to optimize PID parameter tuning for brushless DC (BLDC) motor systems. By using a data-driven approach, machine learning models can replace traditional PID tuning methods, significantly enhancing the system’s adaptability and control performance [11]. An experimental system incorporating a BLDC motor was built, and the motor’s transfer function was obtained in MATLAB. PID parameters were calculated using traditional methods to create an experimental dataset. Seven machine learning algorithms were then used for PID parameter estimation. The results showed that under step input, the PID parameters obtained by traditional methods and machine learning methods were similar, but the machine learning methods were more adaptive to noise and disturbances, with smoother PID parameter adjustments. Under sine input, the PID parameters from machine learning methods showed control effects similar to those of traditional methods. This demonstrates that machine learning methods can successfully estimate PID parameters, replacing the complex calculations of traditional methods. Of the algorithms, Stochastic Gradient Descent (SGD) achieved the highest accuracy at 99.988%, while Support Vector Regression (SVR) had the lowest accuracy at 75.551%.

4. Conclusion

This paper investigates the principles and limitations of traditional PID controllers, and explores modern improvements such as MZOA-based PID optimization, APID control, and the integration of machine learning with PID control. The results indicate that these methods effectively boost the adaptability, response speed, and stability of PID controllers. MZOA-based optimization greatly reduces regulation time and improves system stability. Adaptive PID control dynamically adjusts parameters, allowing the system to adapt to nonlinear variations. Machine learning approaches (e.g., reinforcement learning and neural networks) further enhance the intelligence of PID control, thus making it suitable for complex automation systems. However, these methods still face challenges like high computational complexity and insufficient real-time performance. Future research could focus on reducing computational costs, improving online optimization capabilities, and integrating deep learning techniques to develop more efficient intelligent PID controllers.