1. Introduction

The inherent complexity of deep learning models and the diversity of data distributions impose heightened demands on optimization algorithms. Specifically, the non-convex and non-smooth optimization landscapes characteristic of deep neural networks lack rigorous convergence guarantees, while conventional methods remain theoretically underdeveloped for these challenges. During back propagation, SGD often struggles with problems like gradient vanishing and being overly sensitive to small changes in input, which leads to slow updates of parameters in deep layers and too much bouncing around in gradient values. These inherent limitations substantially elevate the demands placed upon optimization algorithms [1]. Deep neural networks have been extensively employed in natural language processing, computer vision, and multimodal classification tasks, where parameter optimization fundamentally relies on solving non-convex stochastic problems [2]. Representative adaptive learning rate algorithms, including AdaGrad, RMSProp, Adam [3], and AMSGrad, have emerged as pivotal techniques for enhancing model performance through dynamic learning rate adjustment, momentum acceleration, variance reduction, and gradient update strategies. This work presents a systematic analysis of the mechanistic roles played by adaptive optimization algorithms across diverse architectures (CNNs, RNNs, GANs, Transformers, etc.), elucidating their contributions to breakthroughs in training efficiency, generalization capability, and optimization stability, while outlining future research challenges. This research provides deeper insights into the adaptation mechanisms of optimization algorithms across architectures, offering theoretical support for improving training stability and efficiency, and practical guidance for future algorithm design and refinement.

2. Adaptive optimization algorithms: theoretical foundations and core mechanisms

The optimization of parameters in deep neural networks fundamentally constitutes a stochastic optimization challenge within high-dimensional non-convex spaces, with its core objective being the minimization of the empirical risk function [4]:

\( \underset{θ∈{R^{d}}}{min}{\frac{1}{n}\sum _{i=1}^{n}{f_{i}}(θ)}\ \ \ （1） \)

where θ refers to the parameter vector in the d-dimensional space Rd, \( {f_{i}}(θ) \) denotes the loss function associated with the i-th sample, and n is the total number of samples in the dataset. The goal is to find the optimal parameter vector θ that minimizes the average loss across all samples. This formulation encapsulates the essence of the optimization problem in deep learning, highlighting the complexity and dimensionality of the space in which the optimization must be performed.

However, the fixed learning rate mechanism inherent to conventional gradient descent (SGD) demonstrates substantial limitations in addressing gradient heterogeneity and noise sensitivity. To overcome these challenges, adaptive optimization algorithms have emerged as critical methodologies for improving model training efficiency and stability through dynamic modeling of gradient statistics and reformulation of update rules. The theoretical foundation of these algorithms centers on two principal mechanisms: Dynamic modeling of gradient statistics adjusts learning rates using historical gradient information. For instance, AdaGrad operates by accumulating a gradient squared matrix[5]:

\( {G_{t}}=\sum _{τ=1}^{t}{g_{τ}}⊙{g_{τ}}\ \ \ （2） \)

where, \( {G_{t}} \) refers to the accumulated squared gradient matrix at iteration t, forming a diagonal approximation of second-order momentum for per-parameter learning rate adaptation, \( {g_{τ}} \) denotes the stochastic gradient vector at iteration ii, computed from a randomly sampled mini-batch, \( ⊙ \) represents the element-wise Hadamard product operation, while t is the current optimization step index that governs historical gradient accumulation depth. Accordingly, the parameter updates undergo per-dimension scaling as follows:

\( {θ_{t+1}}={θ_{t}}-η\cdot diag{({G_{t}}+ϵI)^{-1}}⊙{g_{t}}\ \ \ （3） \)

where \( {G_{t}} \) is the sum of squared gradients up to time t, η is the learning rate, ϵ is a small value added for numerical stability, and \( ⊙ \) denotes the Hadamard product. This mechanism enables dimension-wise scaling of parameter updates, automatically amplifying learning rates for sparsely activated features (with low gradient update frequencies) while attenuating rates for high-frequency update directions, thereby alleviating the heterogeneity inherent in parameter optimization. However, AdaGrad's monotonically accumulated second-order momentum may lead to premature learning rate decay [6]. To address this limitation, subsequent studies have introduced exponential moving average (EMA) strategies, exemplified by RMSProp and. Adam [7]. The integration of momentum-driven acceleration [7] and variance-adaptive scaling further optimizes gradient dynamics. The Adam algorithm synthesizes first-order moments (capturing directional gradient memory) with second-order moments (statistical estimates of gradient magnitudes [8]:

\( \hat{{m_{t}}}={β_{1}}{m_{t-1}}+(1-{β_{1}}){g_{t}} , \hat{{ν_{t}}}={β_{2}}{ν_{t-1}}+(1-{β_{2}}){g_{t}}⊙{g_{t}}\ \ \ （4） \)

where \( {β_{1}} \) ​ and \( {β_{2}} \) are the decay rates for the first and second moments, respectively. Bias-corrected moments are then derived as:

\( \hat{{m_{t}}}=\frac{{m_{t}}}{1-β_{1}^{t}} , \hat{{v_{t}}}=\frac{{v_{t}}}{1-β_{2}^{t}}\ \ \ （5） \)

The parameter update rule combines these components:

\( {θ_{t+1}}={θ_{t}}-η\cdot \frac{\hat{{m_{t}}}}{\sqrt[]{\hat{{v_{t}}}}+ϵ}\ \ \ （6） \)

where, \( η \) refers to the global learning rate controlling overall update magnitude, \( \hat{{m_{t}}} \) denotes the bias-corrected first-moment estimate of gradients, \( \hat{{v_{t}}} \) represents the bias-corrected second-moment estimate for gradient variance normalization, while \( ϵ \) is a small constant (typically 10−810−8) preventing division-by-zero instability.

This unified framework balances the retention of historical gradient trends (exploitation) and adaptation to instantaneous gradient statistics (exploration), achieving enhanced stability and convergence rates in non-convex optimization landscapes. The momentum term preserves historical gradient directions to expedite convergence, while the variance term suppresses stochastic noise fluctuations, with their coordinated interaction balancing the trade-off between exploration and exploitation efficiency. Theoretically, the performance guarantees of such algorithms can be rigorously quantified through dynamic regret upper bounds.

\( \sum _{t=1}^{T}{f_{t}}({θ_{t}})-\sum _{t=1}^{T}{f_{t}}(θ_{t}^{*})≤O(\sqrt[]{dTlog{T}})\ \ \ （7） \)

The cumulative loss deviation from the dynamic optimal policy is bounded by a sublinear function of the problem dimension d and the time horizon T[9].

Further, Adaptive optimization algorithms can be systematically categorized into three classes based on their design objectives:Gradient-statistic-based methods (e.g., AdaGrad, RMSProp) dynamically adjust learning rates by leveraging local gradient magnitudes[8];Momentum-integrated approaches (e.g., Adam, NAdam[10]) combine directional memory with adaptive scaling mechanisms;Theoretically refined variants (e.g., AMSGrad, AdamW) enhance robustness through constrained optimization or regularized updates. These algorithms exhibit distinct advantages across architectures such as CNNs and Transformers. For instance, Adam's momentum mechanism mitigates gradient vanishing in RNNs, while layer-wise adaptive strategies (e.g., LAMB) enable efficient large-scale Transformer training [11].

The fundamental contribution of adaptive optimization lies in unifying data-driven dynamic modeling with theoretical guarantees, delivering efficient and stable solutions for non-convex optimization[3]. Moving forward, addressing the complexity of large-scale and multimodal training necessitates novel paradigms in distributed coordination and hardware-aware optimization to overcome high-dimensional challenges.

3. Co-evolution of adaptive optimization algorithms and core deep learning models

The rapid advancement of deep learning has driven the increasing complexity of model architectures and the expansion of data scales, demanding higher requirements for optimization algorithms. As a core tool for training deep learning models, adaptive optimization algorithms have significantly enhanced training efficiency and model performance through synergistic co-evolution with key architectures. This chapter explores the mechanisms and profound impacts of adaptive optimization algorithms across convolutional neural networks (CNNs), recurrent neural networks (RNNs/LSTM), generative adversarial networks (GANs), and Transformer models.

3.1. Convolutional Neural Networks (CNNs)

CNNs, the cornerstone of computer vision, rely critically on adaptive optimization algorithms. While CNNs identify important features in images by looking at small areas, adaptive optimizers improve how well these features are learned by adjusting the learning process based on the data. First-order algorithms (e.g., SGD､RMSProp､Adam[3])dominate CNN training due to their computational superiority over second-order methods (e.g., ,Newton[12]､BFGS[13]). These algorithms navigate the high-dimensional solution space defined by loss functions, aligning with the complex tensor structures of CNNs.

For instance, in ResNet training, Adam accelerates shallow feature convergence through parameter-level adaptive learning rate tuning, outperforming SGD in efficiency[14]. However, SGD often achieves superior generalization[15] in specific tasks due to its stable update trajectories, highlighting the trade-off between convergence speed and generalization. In multi-task scenarios, RMSProp mitigates gradient scale imbalance by independently modulating gradients across classification and regression branches, thereby boosting detection accuracy[16]. This synergy not only optimizes CNN training but also underpins their application in multi-task learning. As shown in Figure 1, CNNs consist of convolutional layers, pooling layers, and fully connected layers. These structural components interact closely with optimization dynamics, making the choice of optimizer critical to the success of deep convolutional models.

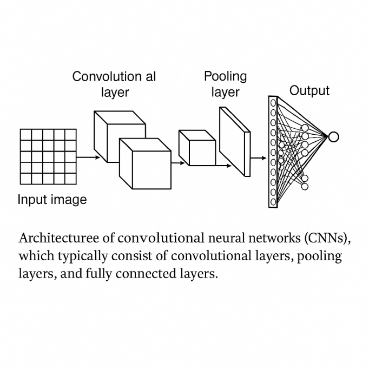
Figure 1: Typical architecture of a Convolutional Neural Network (CNN) showing key functional layers and data flow

3.2. Recurrent Neural Networks (RNNs/LSTM)

RNNs and their variants (e.g., LSTM) excel in sequence modeling but face challenges like long-term dependency learning and vanishing gradients[17]. Adaptive optimizers address these issues effectively: AdaGrad alleviates gradient vanishing by accumulating historical gradients, improving LSTM performance in language modeling.[18] AdamW further stabilizes attention weight updates in machine translation, enhancing output quality. However, temporal dependencies in RNNs amplify gradient noise due to biased second-moment estimates, necessitating gradient clipping for stability[19]. This co-evolution resolves RNN training bottlenecks and enables robust applications in NLP and time-series analysis.

RNNs and their variants (e.g., LSTM) excel in sequence modeling but face challenges like long-term dependency learning and vanishing gradients. (Figure Y provides a schematic representation of RNNs and LSTMs, emphasizing their recurrent structure and gating mechanisms that enable memory retention over long sequences.)

Adaptive optimizers address these issues effectively: AdaGrad alleviates gradient vanishing by accumulating historical gradients, improving LSTM performance in language modeling. AdamW further stabilizes attention weight updates in machine translation, enhancing output quality. However, temporal dependencies in RNNs amplify gradient noise due to biased second-moment estimates, necessitating gradient clipping for stability. (As seen in Figure Y, recurrent connections in RNNs and gating mechanisms in LSTMs play a crucial role in handling sequential data, requiring specialized optimization techniques to ensure stable training.)

This co-evolution resolves RNN training bottlenecks and enables robust applications in NLP and time-series analysis.

As demonstrated in Figure 2, RNNs rely on recurrent units to maintain hidden states across time steps, while LSTMs incorporate gates to control the flow of information. These mechanisms are heavily influenced by the choice of optimization strategy.

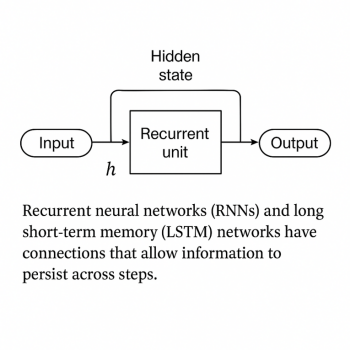
Figure 2: Architecture of RNNs and LSTMs showing input recurrence, hidden states, and memory gating mechanisms

3.3. Generative Adversarial Networks (GANs)

The adversarial nature of GANs poses unique optimization challenges. As depicted in Figure 3, the core framework of GANs consists of a generator-discriminator dyad engaged in a minimax game—the generator synthesizes counterfeit samples while the discriminator distinguishes them from real data. This dynamic equilibrium critically relies on optimization algorithms to coordinate conflicting gradient update directions between the two networks. Adaptive algorithms play a pivotal role here—Adam prevents mode collapse by independently optimizing generator and discriminator networks[20], while RMSProp in Wasserstein GANs improves generation quality via dynamic learning rate scheduling. For example, AdamW in StyleGAN2 decouples weight decay, significantly improving the quality of generated images[21]. Notably, as shown in Figure 3, the discriminator’s feedback gradient (∇D) directly regulates the generator’s parameter adjustments (∇G), necessitating optimizers to maintain stable gradient propagation ratios between these adversarial components. Such innovations stabilize GAN training and expand their applications in image synthesis and style transfer.

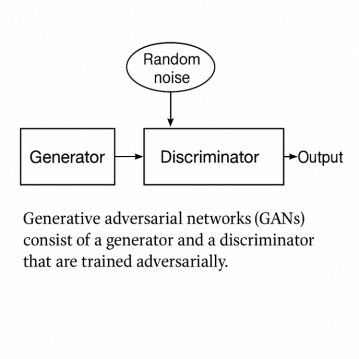
Figure 3: Architecture of GANs illustrating adversarial training between the generator and discriminator with random noise input and synthetic output generation

3.4. Transformer models

The emergence of Transformer models has heralded a new era in deep learning, with adaptive optimization algorithms playing a pivotal role in this paradigm shift. As illustrated in Figure 4, the Transformer architecture comprises stacked encoder and decoder layers. Each encoder layer integrates multi-head attention mechanisms that project inputs into query, key, and value subspaces, followed by position-wise feed-forward networks (FFN) for nonlinear transformation. The decoder further incorporates masked multi-head attention to preserve autoregressive properties during sequence generation. In large-scale pretraining tasks, AdamW significantly reduces the training time of BERT/GPT architectures by efficiently managing sparse gradients, thereby enhancing computational efficiency[18]. Furthermore, the LAMB optimizer enables distributed training for Vision Transformers (ViT), supporting their extension to ultra-large parameter configurations. Recent innovations, such as the Sophia optimizer, further improve convergence efficiency in massive models through second-order Hessian estimation. This co-evolution not only advances the application of Transformers in large-scale pretraining and multimodal tasks but also charts a strategic direction for the future evolution of deep learning technologies.

The co-evolution of adaptive optimization algorithms and deep learning architectures remains a cornerstone of AI progress. From CNNs to Transformers, these algorithms dynamically address training challenges, balancing speed, stability, and generalization. The hierarchical structure of Transformers—with its alternating attention and FFN layers—demands optimizers capable of handling heterogeneous gradient distributions across submodules, a requirement met by layer-wise adaptive strategies like LAMB. Their synergy has propelled advancements in computer vision, NLP, and generative modeling while offering theoretical and practical insights for future research[22]. As deep learning evolves, adaptive optimizers will continue to underpin innovations, steering AI toward unprecedented frontiers.

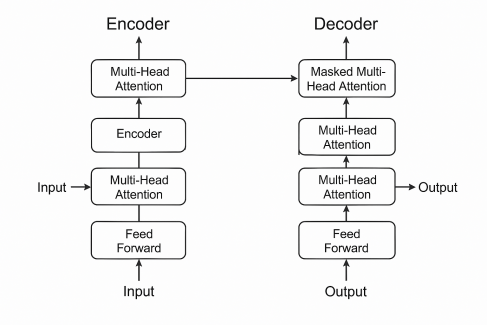
Figure 4: Architecture of transformers highlighting encoder-decoder stacks, multi-head attention layers, and masked attention mechanisms for sequential information propagation

4. Cross-domain applications and performance comparative analysis of adaptive optimization algorithms

The efficacy of adaptive optimization algorithms is highly dependent on model architectures and task characteristics, and their application differences in heterogeneous scenarios can be elucidated through comparative analysis of representative cases. The table below summarizes the synergistic mechanisms between mainstream models and optimization strategies:

Table 1: Comparative analysis of optimization strategies for deep learning architectures: methods, advantages, and challenges

In the field of computer vision, object detection models significantly enhance detection robustness in complex scenarios by dynamically modulating gradient update steps for multi-task loss functions through gradient balancing strategies [23]. For instance, architectures based on region proposal networks coordinate classification accuracy and localization errors via differentiated gradient scaling mechanisms. However, high-resolution image processing remains constrained by memory efficiency bottlenecks. In natural language processing, big pre-trained language models use low-rank optimizers (like AdaFactor) to reduce the size of the parameter update matrices, which helps ease memory usage. Nevertheless, sparse gradient-induced statistical deviations in low-resource language modeling tasks still hinder convergence stability.

In multimodal learning scenarios, vision-language joint models leverage the hierarchical adaptive mechanisms of the LAMB optimizer to achieve balanced cross-modal feature optimization through gradient and parameter norm normalization. While such methods exhibit significant advantages in distributed training, gradient direction conflicts in multi-objective loss functions necessitate the introduction of competition-aware optimization strategies. In privacy-sensitive scenarios, federated learning frameworks utilize noise-robust optimizers (e.g., DP-AdamW) to compensate for gradient variance perturbations introduced by differential privacy mechanisms, maintaining model utility while controlling privacy leakage risks. However, communication efficiency in ultra-large-scale models still requires improvement.

Current technical challenges are centered on asynchronous routing bias in dynamic sparse activation systems, multi-modal objective competition convergence, and optimization efficiency bottlenecks induced by hardware heterogeneity. Future research must focus on developing universal optimization frameworks that support dynamic computation graphs and mixed-precision training to address the complexity demands of cross-domain deployment for ultra-large-scale models.

5. Challenges and future directions

While adaptive optimization algorithms remain instrumental in propelling advancements within deep learning, the technical constraints they confront in the epoch of ultra-large models have undergone profound transformations, giving rise to several cardinal challenges:

A paramount difficulty resides in the harmonious optimization of dynamic sparse activation and heterogeneous computational resources. The dynamic sparse activation paradigm, characteristic of mixed expert systems architectures deployed in ultra-large language models (e.g., GPT-4, PaLM), invalidates conventional optimizers for global gradient statistics. Specifically, the asynchronous routing protocols inherent to expert networks precipitate systematic deviations in the second-moment estimations of Adam optimizers, necessitating the formulation of adaptive learning rate modulation mechanisms that incorporate localized routing awareness.

Secondly, the antagonism among optimization objectives in multimodal tasks has surged to the forefront. Within vision-language fusion models, the loss functions pertaining to text generation and image reconstruction manifest intrinsic competitive dynamics[24], complicating the reconciliation of multi-objective convergence trajectories for extant optimization algorithms (a concern underscored at ICML 2024).

Thirdly, the deterioration of optimization stability under privacy-preserving constraints has surfaced as a critical issue. In federated learning paradigms, the injection of noise mechanisms to ensure differential privacy amplifies gradient variance, precipitating high-frequency oscillations in adaptive optimization algorithms[25]. This predicament underscores the exigency for the development of noise-resilient parameter recalibration methodologies (epitomized by the DP-AdamW proposal at CVPR 2024).

Furthermore, the discrepancies in optimization efficiency engendered by hardware heterogeneity have intensified. In hybrid computational clusters integrating TPUs and GPUs, disparities in floating-point precision and communication protocols engender substantial increases in gradient synchronization latencies. Conventional distributed optimization strategies falter in achieving cross-device load equilibrium. Concomitantly, the disintegration of convergence during ultra-low-precision training has emerged as a formidable impediment to model lightweight deployment. Empirical evidence suggests that low-bit quantization drastically compromises the fidelity of second-moment estimations within Adam-type optimizers, thereby jeopardizing model performance[26]. This necessitates the urgent conception of error mitigation frameworks. These challenges not only demand paradigm-shifting innovations at the algorithmic stratum but also advocate for a fundamental re-architecting of the optimization theory corpus to accommodate the escalating complexity of contemporary artificial intelligence models.

6. Conclusion

Adaptive optimization algorithms have emerged as a cornerstone in advancing deep learning by dynamically adapting to model architectures and data characteristics. Through their co-evolution with core frameworks like CNNs, Transformers, and GANs, these algorithms have significantly enhanced training efficiency, generalization capability, and stability across diverse domains. However, the era of ultra-large-scale models introduces unprecedented challenges: dynamic sparse activation in mixed expert systems disrupts gradient statistics, multimodal objective conflicts impede balanced convergence, privacy-preserving noise amplification destabilizes optimization trajectories, and hardware heterogeneity exacerbates computational inefficiencies. Addressing these challenges demands a paradigm shift toward unified theoretical frameworks that integrate dynamic computation graphs, noise-resilient parameterization, and hardware-aware distributed coordination. Future research must bridge theoretical rigor with engineering pragmatism, fostering innovations in automated hyperparameter tuning, lightweight training protocols, and cross-modal optimization strategies. By harmonizing algorithmic adaptability with systemic scalability, adaptive optimization will remain pivotal in steering AI toward robust, efficient, and ethically grounded frontiers.