1. Introduction

As the foundation stone of current energy storage system, lithium-ion batteries offer powers from electric vehicles to grid-scale storage. Nonetheless, security issues impede their extensive application, notably the risk of thermal runaway, namely, a catastrophic failure featured by uncontrollable temperature changes which could trigger fire hazards or explosions. The conventional method of thermal runaway prediction is contingent upon physics-based models [1] or statistical methods, such as Gaussian process regression [2], which frequently have difficulty in capturing the intricate, nonlinear dynamics of the battery`s capacity loss under practical working conditions.

The latest progress in deep learning (DL) have proved advantageous performance of sequential data modeling for battery systems, with long short-term memory (LSTM) networks [3] which are highly efficacious in capturing time dependencies in voltages and temperature signals. Though variants such as bidirectional LSTMs [4] and attention mechanisms [5] have deeply enhanced precision, such models commonly need plenty of computing resources. Such limitation is exceedingly severe in view of the demand for high-frequency supervision among large battery packs showing hundreds of batteries.

The computational efficiency challenge has spurred interest in techniques like model pruning [6] and dynamic neural networks [7]. However, existing approaches often employ static pruning strategies that remove network components permanently, potentially degrading performance on complex anomaly patterns. Moreover, most current methods treat all input sequences equally, failing to adapt computational effort based on the inherent complexity or risk level of the observed battery state. This one-size-fits-all approach leads to inefficient resource utilization, as simple nominal operating conditions require the same computational overhead as critical pre-runaway states.

We address these limitations through a novel combination of over-parameterized LSTM training and dynamic inference-time pruning. Our approach differs fundamentally from prior work in three key aspects. First, we introduce input-dependent sparsity, where a lightweight policy network evaluates the complexity of incoming battery data and selectively activates LSTM cells through learned thresholds. Second, we retain full model capacity during the training period and initiate adaptive computation during the deployment period. This guarantees the robustness under various working conditions. Third, our method automatically learns the association between input features and required model intricacy while removing the demand for manual threshold tuning or heuristic rules. Our main contributions are summarized as follow.

• A new dynamic pruning framework for LSTM is formulated to adapt computational effort on the grounds of real-time input intricacy;

• An end-to-end trainable policy network is developed to learn optimum pruning strategies with no human intervention;

• Multiple battery datasets are systematically assessed with advantageous performance relative to static models;

• Computing efficiency gains are analyzed to achieve the deployment in resource-limited environments.

The remainder of this paper is organized as follows: Section 2 reviews related work in battery anomaly detection, dynamic neural networks and pruning techniques. Section 3 describes the methodology proposed, including the policy network design and dynamic pruning mechanism. Sections 4 presents experiment and result discussions, respectively. Finally, the conclusions are presented in Section 5.

2. Methodology

2.1. Thermal runaway in battery system

Thermal runaway signifies a positive feedback loop, in which increased temperature speeds up exothermic chemical reactions and thus increases the temperature until catastrophic failure happens. Such process is universally reflected via measurable precursors in voltage and temperature signals. It is demonstrated that rate-of-change metrics is highly informative for early detection:

\( Δ{T_{t}}=|{T_{t}}-{T_{t-1}}| \) (1)

\( Δ{V_{t}}=|{V_{t}}-{V_{t-1}}| \) (2)

These differential characteristics capture the acceleration phase, followed by thermal runaway; here, the traditional threshold-based methods frequently fail in detecting nuanced deviations [8]. The nonlinear coupling between thermal and electrical dynamics entails models able to learn complicated temporal patterns throughout multiple timescales.

2.2. Long Short-Term Memory

Recurrent Neural Network (RNN) naturally adapts to processing data with time series or sequence structures, and flexibly handle input sequences of different lengths while capturing dependencies within the sequences. Nevertheless, these networks undergo vanishing gradients in terms of learning long-ranging dependencies [3]. LSTMs are selected as an alternative to deal with such limitation via gated memory cells. The calculation formula for each gate function and state transfer process in the LSTM module is as follows:

\( {f_{t}}=σ({W_{f}}∙[{h_{t-1}},{x_{t}}]+{b_{f}}) \) (3)

\( {i_{t}}=σ({W_{i}}∙[{h_{t-1}},{x_{t}}]+{b_{i}}) \) (4)

\( \bar{{C_{t}}}=tanh⁡({W_{g}}∙[{h_{t-1}},{x_{t}}]+{b_{g}}) \) (5)

\( {o_{t}}=σ⁡({W_{o}}∙[{h_{t-1}},{x_{t}}]+{b_{o}}) \) (6)

\( {C_{t}}={f_{t}}*{C_{t-1}}+{i_{t}}*\bar{{C_{t}}} \) (7)

\( {C_{t}}{h_{t}}={o_{t}}∙tanh⁡({C_{t}}) \) (8)

where \( f \) denotes forgetting gate output, \( i \) denotes input gate output, \( o \) denotes output gate output, \( h \) denotes hidden layer output, \( x \) denotes input, \( W \) denotes connection weight parameter, \( b \) denotes offset parameter, and \( C \) denotes the intermediate variable, subscript \( t \) denotes for \( t \) th time step.

Through well-designed forget and input gates, the cell state \( {C_{t}} \) maintains information over extended sequences. Such architecture has proven advantageous performance for battery anomaly detection, relative to simpler recurrent units [9-10], despite at raised computational cost.

2.3. Dynamic network pruning and conditional computation

Dynamic pruning techniques adapt to model intricacy during the inference period based on input features. As to a neural network with L layers, the pruning mask for layer at time step can be expressed as below:

\( M_{t}^{(i)}=Г(g({x_{t}}) \gt τ) \) (9)

where \( g(∙) \) is used for figuring out input-dependent importance scores, \( τ \) indicates a threshold parameter. Compared to static pruning [11], this method retains model capacity and achieves computational savings during the inference. The latest progresses have exhibited that such methods can fulfill remarkable speedups without accuracy losses when trained suitably [12-14]. The challenge lies in the design of efficient gating systems which credibly identify redundant computations without no excessive overhead.

2.4. Dynamic pruning mechanism for LSTM inference

The central innovation of our method is the dynamic pruning of LSTM cells during the inference. This is achieved through a gating system which assesses input intricacy. For an over-parameterized LSTM with N cells, we define the pruning mask \( {M_{t}}∈\lbrace 0,1{\rbrace ^{N}} \) at timestep \( t \) as:

\( M_{t}^{(i)}=Г({α^{(i)}}Δ{T_{t}}+{β^{(i)}}Δ{V_{t}} \gt {τ^{(i)}}) \) (10)

where \( {α^{(i)}} \) and \( {β^{(i)}} \) are learnable weights which measure each cell’s sensitivity to voltage and temperature variations. \( {τ^{(i)}} \) indicates an adaptive threshold. The pruned hidden state \( {\widetilde{h}_{t}} \) is figured out through element-wise multiplication showing the mask:

\( { \widetilde{h}_{t}}={M_{t}}⊙{h_{t}} \) (11)

The above formulation makes the model sustain full capacity for critical anomaly patterns, and decreases computation for nominal working conditions. The thresholds \( {τ^{(i)}} \) are uniformly initialized, yet learned for each cell, separately during the training, which achieves fine-grained adaptation to discrepant input features.

2.5. Transformer-based policy network architecture

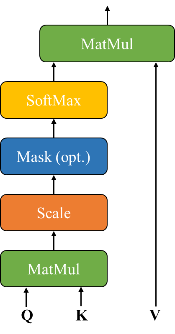
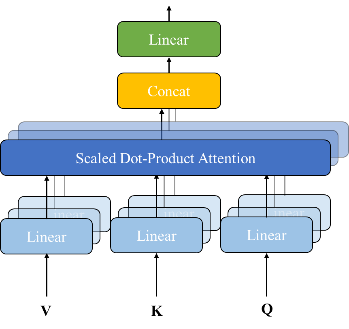
The policy network is responsible for producing pruning masks through a lightweight Transformer encoder [15] to treat input characteristics. Given the input vector \( {x_{t}}=[Δ{T_{t}},Δ{V_{t}},{T_{t}},{V_{t}}] \) , the network computes attention weights:

\( Attention(Q,K,V)=softmax(\frac{Q{K^{T}}}{\sqrt[]{{d_{k}}}})V \) (12)

where \( Q \) , \( K \) , and \( V \) are learned projections of \( {x_{t}} \) , and \( {d_{k}} \) represents the key dimension. The encoder comprises two layers with four attention heads, and produces a 128-dimensional embedding which feeds into a sigmoid-activated dense layer to forecast pruning probabilities \( p_{t}^{(i)} \) for each LSTM cell:

\( p_{t}^{(i)}=σ({W_{p}}{z_{t}}+{b_{p}}) \) (13)

where \( {z_{t}} \) indicates the Transformer’s output embedding. The final binary mask \( {M_{t}} \) is obtained by thresholding these probabilities, with the threshold values \( {τ^{(i)}} \) being learned parameters rather than fixed hyperparameters. The details of self-attention and multi-head attention are shown in Figure 1.

Figure 1: The details of self-attention and multi-head attention [15]

2.6. Joint anomaly scoring with pruned features

The anomaly score \( {s_{t}} \) combines information from both the pruned LSTM features and policy network outputs:

\( {s_{t}}=σ({W_{s}}[{\widetilde{h}_{t}};{z_{t}}]+{b_{s}}) \) (14)

where \( {W_{s}} \) and \( {b_{s}} \) are learnable parameters, and \( {\widetilde{h}_{t}} \) represents the pruned hidden state. This joint representation captures both temporal patterns from the LSTM and input complexity metrics from the policy network, providing a more comprehensive assessment of thermal runaway risk than either component alone. The score ranges from 0 (normal operation) to 1 (imminent thermal runaway), with a threshold of 0.5 used to trigger safety protocols in practice.

2.7. End-to-end training with adaptive sparsity

The complete system is trained end-to-end using a composite loss function:

\( L={λ_{1}}{L_{anomaly}}+{λ_{2}}{L_{sparsity}}+{λ_{3}}{L_{policy}} \) (15)

The anomaly detection loss \( {L_{anomaly}} \) uses focal loss [16] to address class imbalance:

\( {L_{anomaly}}=-α{(1-{s_{t}})^{γ}}{y_{t}}log({s_{t}}) \) (16)

where \( {y_{t}} \) is the ground truth label, α balances class frequencies, and \( γ \) focuses learning on hard examples. The sparsity regularization term encourages efficient computation:

\( {L_{sparsity}}=\frac{1}{N}\sum _{i=1}^{N}p_{t}^{(i)} \) (17)

while the policy loss \( {L_{policy}} \) ensures reliable pruning decisions:

\( {L_{policy}}=E[max(0,{τ^{(i)}}-({α^{(i)}}Δ{T_{t}}+{β^{(i)}}Δ{V_{t}}))] \) (18)

This formulation penalizes the policy network when it prunes cells during critical events, ensuring safety-critical computations are preserved. The loss components are balanced using coefficients \( {λ_{1}} \) , \( {λ_{2}} \) , and \( {λ_{3}} \) , which are tuned via cross-validation.

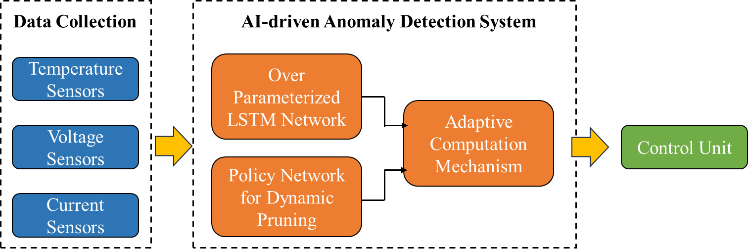
Figure 2: Framework for lithium-ion battery thermal runaway prediction

The system architecture illustrated in Figure 2 processes streaming battery sensor data through three coordinated components: 1) feature extraction modules that compute differential metrics, 2) the policy network that generates dynamic pruning masks, and 3) the pruned LSTM that produces final anomaly scores.

3. Experiment and result

3.1. Experiment

To evaluate the proposed dynamic pruning LSTM, we prepare lithium-ion batteries from 3 different energy storage battery manufacturers and then overcharge these batteries to cause thermal runaway. The charging rate is 0.5C. When the charging current of the battery decreases, increase the charging voltage to maintain the charging current at 0.5C until the battery loses thermal control and bursts or catches fire.

3.2. Result and discussion

We compare against five state-of-the-art approaches for battery anomaly detection:

• Vanilla LSTM: A standard LSTM network with 128 hidden units trained end-to-end on raw sensor data [10].

• Attention-LSTM: Augments the LSTM with temporal attention mechanisms for improved feature weighting [5].

• Wavelet-CNN: Uses wavelet transforms for multiscale feature extraction followed by convolutional layers [17].

• Gaussian Process (GP) Regression: A probabilistic model with Matérn kernel for uncertainty-aware prediction [2].

• One-Class SVM: Trained on nominal operation data to detect deviations [9].

Each baseline is implemented with optimal hyperparameters from their respective publications and retrained on our combined dataset to ensure fair comparison. Performance is assessed using four metrics: detection recall, False Alarm Rate (FAR), average detection delay and inference Latency

The proposed model is implemented with the following configuration:

• LSTM network: 4 layers with 256 cells each, dropout rate of 0.2 between layers.

• Policy network: 2-layer Transformer encoder with 4 attention heads and 128-dimensional embeddings.

• Training: Adam optimizer with initial learning rate 1e-3, batch size 64, and early stopping based on validation loss.

• Dynamic pruning: thresholds initialized uniformly in [0.1, 0.3] and learned during training.

3.2.1. Comparative performance analysis

To evaluate the effectiveness of our dynamic pruning LSTM (DP-LSTM) approach, we compare its anomaly detection performance against baseline methods across all three datasets. Table 1 presents the aggregated results, showing mean values and standard deviations from 10 independent runs.

The proposed DP-LSTM achieves superior performance across all metrics, demonstrating both higher recall (98.7%) and lower false alarm rates (2.1%) compared to alternatives. Notably, it reduces detection delay by 40% relative to the best-performing baseline (Attention-LSTM), while maintaining sub-2ms inference latency suitable for real-time deployment. The standard deviations indicate consistent performance across different dataset splits, suggesting robustness to data variability.

Table 1: Performance comparison of thermal runaway detection methods

The proposed DP-LSTM achieves superior performance across all metrics, demonstrating both higher recall (98.7%) and lower false alarm rates (2.1%) compared to alternatives. Notably, it reduces detection delay by 40% relative to the best-performing baseline (Attention-LSTM), while maintaining sub-2ms inference latency suitable for real-time deployment. The standard deviations indicate consistent performance across different dataset splits, suggesting robustness to data variability.

3.2.2. Dynamic pruning efficiency

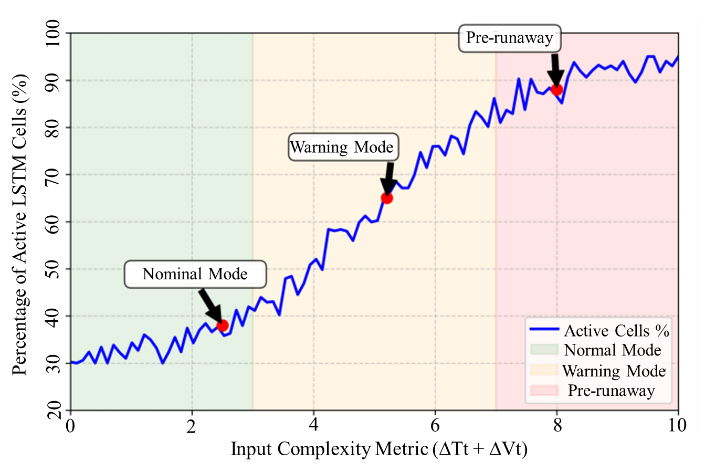
To quantify the computational benefits of our dynamic pruning mechanism, we analyze the average percentage of active LSTM cells during inference under different battery states. Figure 3(a) illustrates the relationship between input complexity (measured by \( △{T_{t}} \) + \( △{V_{t}} \) ) and computational savings.

The results demonstrate that DP-LSTM automatically adjusts its computational load based on input characteristics. During nominal operation (low \( △{T_{t}} \) + \( △{V_{t}} \) ), the model activates only 35-45% of cells, reducing inference time by 55-65% compared to full network evaluation. As anomaly indicators intensify, the policy network progressively enables more cells, reaching 85-95% utilization during critical pre-runaway states. This adaptive behavior explains the latency advantages shown in Table 1 while maintaining high detection accuracy.

3.2.3. Cross-dataset generalization

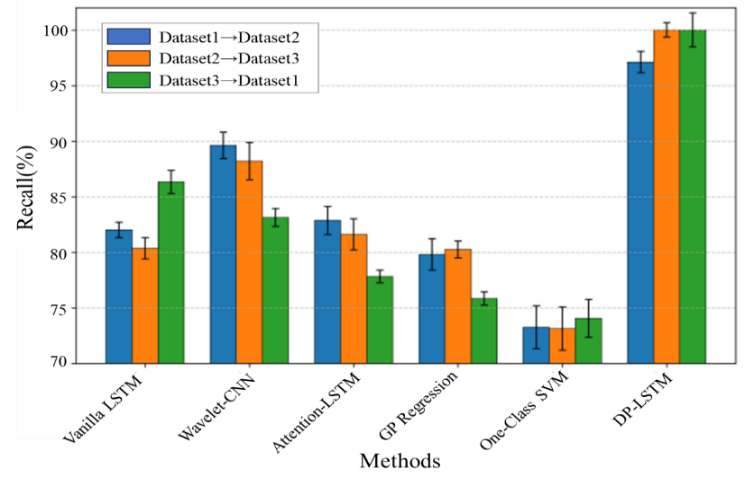
To assess generalization capability, we perform cross-dataset evaluation where models are trained on one dataset and tested on another. Figure 3(b) shows the recall rates for each transfer scenario.

Figure 3: Results of dynamic pruning efficiency and cross-dataset generalization

DP-LSTM maintains consistently high performance (recall>96%) across all transfer scenarios, outperforming baselines by 8-15 percentage points. This robustness stems from the policy network’s ability to learn generalizable pruning strategies based on fundamental battery dynamics rather than dataset-specific artifacts. The Wavelet-CNN shows particularly poor generalization, likely due to its reliance on handcrafted feature extraction tuned to specific data characteristics.

4. Conclusions

Our work presents the dynamic pruning architecture of LSTM, which balances computational efficiency with high detection accuracy and thus tackles crucial challenges in predicting thermal runaway in real time for battery systems. The system integrates an adaptive policy network and an over-parameterized LSTM, which achieves remarkable reductions in inference latency and sustains robust performance under various operating conditions. Experimentally, it is demonstrated that the proposed method exceeds extant approaches in recall rates and false alarm rates, notably the additional benefit of the sub-millisecond inference time appropriate to embedded deployment.

This makes the system more applicable to different battery chemistries and usage scenarios. The proposed framework takes a meaningful step to effective, AI-powered battery safety solutions, with significant influences on key energy applications, including electric vehicles, grid storage, etc.

Acknowledgement

This work was supported in Research and Development of Portable Rapid Detection Technology and Integrated System for Battery Energy Storage Power Stations under Grant HNKJ24-H59.