1. Introduction
Artificial intelligence (AI) has become more popular in the past decade and more research focuses on the interdisciplinary area of AI; some of its applications include auto-driving, medical, financial field, and others [1-6]. Researchers strive to enhance the AI to human-level thinking. In recent years, since the success of AlphaGo [7, 8], many AIs are tested with video games because it is an efficient and valuable method to improve the performance of AI [9, 10]; the best type is the board games. Board games have been an entertainment for people for centuries, they play an important role in different cultures and societies. Board games can simulate many aspects of real life, and they are composed of tactics, luck, and strategy. With the enormous possible decisions, board games have become an active area for the research and evolution of AI. People today can access many traditional board games from the computer; with the high-performance processor of computer and powerful AI algorithms, the opponent has become nearly invincible.
There are many algorithms that help to build a robust AI. A common algorithm used in these game AIs is the Minimax Tree, which is a decision theory that minimizes the possible loss with a worst-case scenario and maximizes the minimum gain. Making such a decision does not require assumption on the uncertainty of the opponents. However, the minimax tree considers all the decisions that will occur, so its time complexity is \( O({b^{n}}) \) and the space complexity is \( O(bn) \) , where b is the number of legal moves at each point and n is the maximum depth of the tree. This means that the time complexity for it to search for the right decision will grow exponentially as the depth increases. To resolve this problem, alpha-beta pruning is implemented to accelerate the search. Alpha-beta pruning is an algorithm that reduces the number of the nodes in the Minimax Tree; it prunes the branches that are theoretically useless, therefore, the overall algorithm only needs to examine \( {b^{d/2}} \) nodes of the tree, where d is the depth of a node. Nevertheless, tactics and strategies can be applied to further accelerate the search and increase the winning chance. In this paper, it focuses on implementing minimax tree and alpha beta pruning with tactics and strategy in various board games and examines the AI’s decisions through the game. To support the research with precise data, a traditional Chinese board game, Gobang, is used to test the AI. Gobang is a two-player game that does not require any luck to win.
2. Method
Gobang is an ancient strategy board game from China. Gobang is played between two players; the players choose either black or white stone and take turns to place one stone on a 15x15 game board each time. The objective of gobang is to form a row of five consecutive stones of one color; the formation can be in horizontal, vertical, or diagonal. There are some variants of Gobang that exist nowadays, including Free-style, Standard, and other professional versions. In the Free-style version, players don’t need to pursue the line of exact five stones, which means one can still form a line of six or more consecutive stones of the same color. In the standard version, players must pursue the line of exactly five stones and the line of six or more consecutive stones of the same color can’t be regarded as a win. Although the rule is simple for this game and it seems like an enhanced version of tic-tac-toe, it is a complicated game and requires more advanced tactics.
In this paper, the Gobang AI is built with the Free-style rule based on the Minimax Search Tree, Alpha Beta Pruning, and tactics (Heuristics Algorithms). There are three versions of AI: AI with only Minimax Tree (Minimax AI), AI with Minimax Tree and Alpha-Beta Pruning (Alpha-Beta AI), and AI with both algorithms plus specific Heuristics Algorithms (Heuristic AI). The experiment will show the efficiency of implementing Alpha Beta Pruning and the increasing winning chance with specific tactics.
Minimax Tree can be used to find the best value for the player in each range of step prediction. The tree is formed with two kinds of layers: the max layer and the min layer. The max layer is the computer’s turn, so it will consider only the largest value which optimizes the current situation and search for the maximum score in the level. The min layer is the opponent’s turn; since the opponent will try to find the best move, the AI should consider the worst case, therefore, the AI should predict the best value for the opponent. Scoring from the AI perspective, based on the scoring method, the smaller the score is, the higher possibility for the opponent to win, thus the AI will search for the minimum score in the level. With the Minimax Tree, the AI can infer all the possible steps. However, AI search with Minimax Tree is an efficient method in simple games such as tic-tac-toe, which only has a small number of possible board positions, but for games with numerous possible positions. Using gobang as an example, there are already 255 possible moves in the first step, 255*254 in the second, 255*254*253 in the third, and so on; therefore, for nth layer of prediction, the moves to consider will be \( \frac{255!}{(255-n)!} \) , and the time complexity will also increase exponentially. To resolve the problem mentioned in Minimax Tree, the AI will also implement the Alpha Beta Pruning to accelerate the searching time.
Alpha-Beta pruning is a search algorithm to reduce the number of nodes in the Minimax search tree. When the algorithm calculates that the subsequent development of the policy is worse than the previous one, it stops calculating the subsequent development of the policy. This algorithm gives the same results as Minimax search but removes the branches that do not affect the final decision. It is a depth-first search. Alpha records the minimum score allowed by a node, and beta records the maximum score. The score is backtracked from the leaf to the root. Alpha-Beta pruning can be separated as alpha pruning and beta pruning. Alpha pruning is when the β value of a Min node is less than or equal to the α value of any parent node, all children of the node are clipped. Beta pruning is when α value of a Max node ≥ β value of any parent node, all children of the node are clipped.
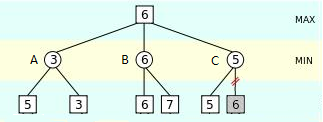
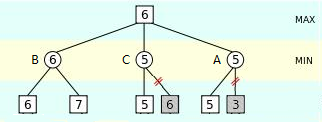
Although using Alpha-Beta Pruning optimizes time complexity, the searching depth of the is still limited and so the AI can only make decisions with a small portion of possible states, it is called the horizon effect. Heuristic Algorithms can be implemented to expand the searching depth and resolve this problem. Figure 1 is an example of Minimax Tree without Heuristic Algorithm. In this case, the Alpha-Beta prunin can only prune the last branch. Figure 2 is the Minimax Tree build with Heuristic Algorithm. The logic is to evaluate the score of node A, B, and C, then sort in descend order when generating the Minimax Tree, this can optimize the time of Alpha-Beta Pruning.
|
Figure 1. Minimax tree without Heuristic algorithm. |
|
Figure 2. Minimax tree implemented Heuristic algorithm. |
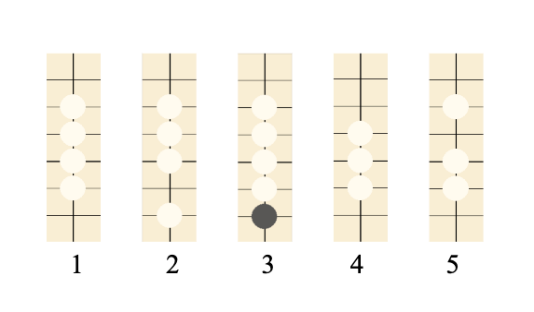
The tactic used for the Heuristic Algorithms is to rank the higher winning stone formation in the Minimax Tree, then continue searching with the top nth cases. Alpha-beta pruning can reduce a tree size \( {b^{d}} \) to \( {b^{d/2}} \) , with a perfect heuristic algorithm, the tree size can be reduced to d. The Heuristic Algorithm design for this Gobang AI evaluates the formation that has a higher score first, then only evaluates the cases of the high scores. Figure 3 shows the high score formation to prioritize during the evaluation. The first one is live-four, it is a definite win with this formation. The second and third are strike-four, if there can be two strike-four forms at the same time, it is also a definite win. The fourth and fifth are live-three, which can form either live-four or strike-four.
|
Figure 3. High score stone formations. |
3. Result and Discussion
For Minimax Tree, the time complexity of minimax is \( O({b^{m}}) \) , it is obvious that the time complexity for one step of the Gobang AI with only the Minimax Tree is very large; as the searching depth of the Minimax Tree expands, the time for one step without Alpha-Beta Pruning increases exponentially. When running the AI with the searching depth of 4, it is nearly impossible for the AIs to complete a game because the time for one step is already very long.
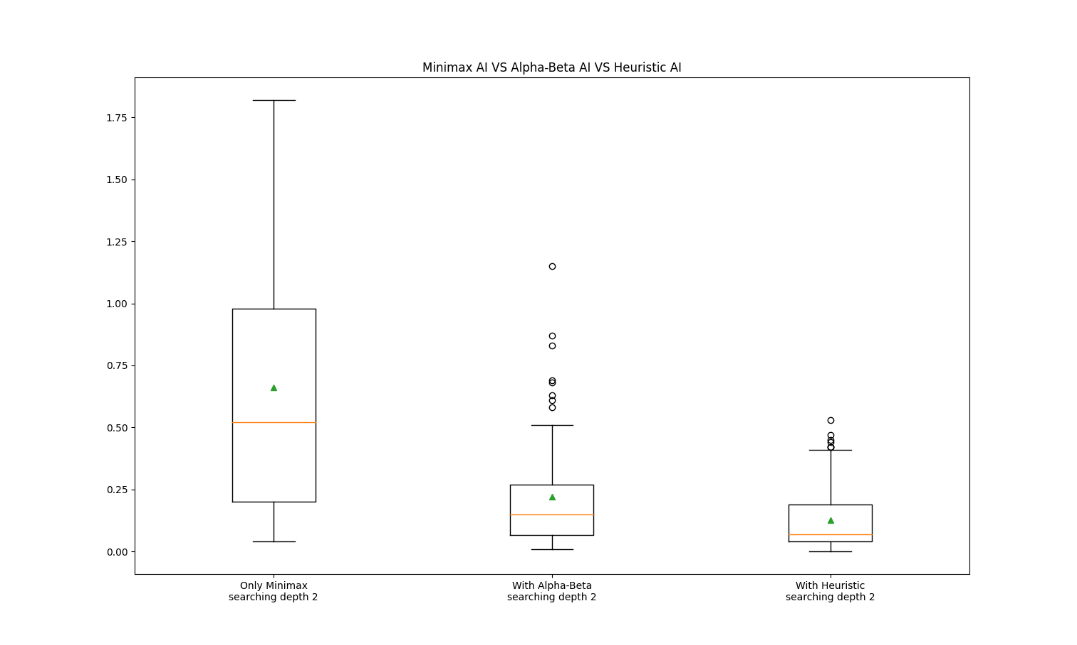
By implementing the Alpha-Beta Pruning with the Minimax Tree, the time complexity has largely shortened. In Figure 4, with the sample of 100 turns, the average time for one step of the AI optimized by Alpha-Beta Pruning, 0.22 sec, has accelerated 300% compared to the AI with just the Minimax Tree, 0.66 sec. Image 3.2 shows one game between the Minimax and Alpha-Beta AI, and it is evident that the Alpha-Beta AI is faster. When the searching depth is 2, 96% of step’s time complexity of the AI with Alpha-Beta Pruning fall between 0.04 and 0.49, and 99.5% in 1 second, whereas only 76% of AI with just Minimax Algorithm’s step time complexity are in 1 second. However, even with Alpha-Beta Pruning, when the searching depth reaches 4, the time for one step is still too long to wait. The main problem of this is the instability of Alpha-Beta Pruning as the Minimax Tree grows larger during the game and the disarrangement of the prediction cases in the tree.
|
Figure 4. Searching time of different AI with Depth 2. |
|
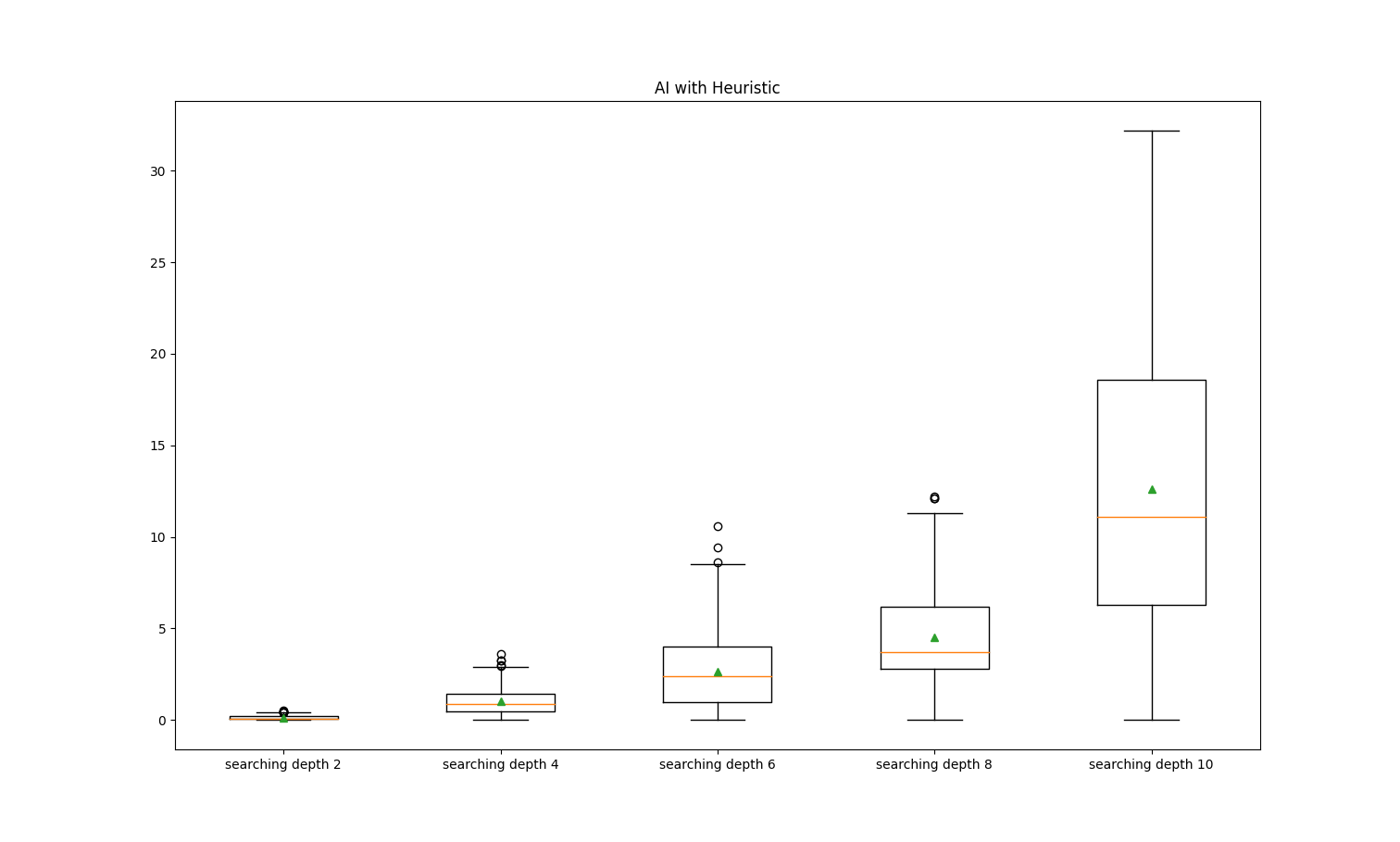
Figure 5. Heuristic AI searching time of different depth. |
To further accelerate the time for one step, tactics need to be implemented during the pruning. The Heuristic Algorithm can promote the Alpha-Beta pruning by ordering the high score formation of stone in the Minimax Tree first. In Figure 5, comparing Heuristic AI with the other two AIs, it shows a significant decrease in time. The median time for one step of the Heuristic AI is only half of the Alpha-Beta AI, and a quarter of the Minimax AI. Decrease in searching time means that the searching depth can be expanded deeper. As shown in Figure3, the searching depth of the Heuristic AI can be increased to 10 or larger with the number of high score considerations to be decreased, and the game can still be finished. In the Minimax Tree, deeper searching depth increases the chance of winning because it can evaluate more possible cases of the game. In the total of 20 games, the Heuristic AI beats the Alpha-Beta AI 8 times out of 10 when Heuristic AI goes first, and 7 times out of 10 when Alpha-Beta AI goes first; a total of 15 times out of 20.
There can be more improvements made on the score evaluation part to increase the winning rate and run time stability of the Heuristic AI. The problem is that with limited high score considerations, the algorithm may prune branches that may contain higher scores for the opponents. This is narrowing the prediction cases of the AI. An extreme case is with 20 search depths but only take the 1 high score consideration; there are many possibilities after the 1 high score case that the opponent has higher winning chance, but the Heuristic Algorithm prunes those branches.
4. Conclusion
As the data has shown, Alpha-Beta Pruning and Heuristic Algorithms can optimize the efficiency of the Minimax Tree AI and increase the winning rate with deeper depth search. It is obvious that only with a Minimax Tree, it is hard for the AI to “think further” due to limitations of hardware. However, with Alpha-Beta Pruning and Heuristic Algorithms, the Gobang Minimax AI has been enhanced. The combination of these algorithms produces an AI with higher winning rate, deeper search depth, and stabler run time. The heuristic of this Gobang AI can also be implemented in other boards with the same strategical idea. This AI is designed to maximize the benefit when facing unknown decisions of the opposite; at the same time, it can accelerate the time to make decisions. Because of these characteristics, this model of AI can also be implemented in other fields of decision making.
References
[1]. Zhou Q 2022 Multi-modal medical image fusion based on densely-connected high-resolution CNN and hybrid transformer. Neural Computing and Applications, 1-21.
[2]. Qiu Y 2020. Clustering Analysis for Silent Telecom Customers Based on K-means++. In 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC) (Vol. 1, pp. 1023-1027). IEEE.
[3]. Valen J 2022. Quantifying uncertainty in machine learning classifiers for medical imaging. International Journal of Computer Assisted Radiology and Surgery, 17(4), 711-718.
[4]. Bacchi S 2022. Machine learning in the prediction of medical inpatient length of stay. Internal medicine journal, 52(2), 176-185.
[5]. Ahmed U 2022. Prediction of diabetes empowered with fused machine learning. IEEE Access, 10, 8529-8538.
[6]. Kayalibay B 2017 CNN-based segmentation of medical imaging data. arXiv preprint arXiv:1701.03056.
[7]. Chen J X 2016 The evolution of computing: AlphaGo. Computing in Science & Engineering, 18(4), 4-7
[8]. Holcomb S D et al. 2018 Overview on deepmind and its alphago zero ai. In Proceedings of the 2018 international conference on big data and education (pp. 67-71).
[9]. Perez L D et al. 2016 General video game ai: Competition, challenges and opportunities. In Thirtieth AAAI conference on artificial intelligence.
[10]. Bakkes S 2009 Rapid and reliable adaptation of video game AI. IEEE Transactions on Computational Intelligence and AI in Games, 1(2), 93-104.
Cite this article
Ma,D.Y. (2023). Optimization of Alpha-Beta pruning based on heuristic algorithm. Applied and Computational Engineering,6,1143-1147.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Signal Processing and Machine Learning
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Zhou Q 2022 Multi-modal medical image fusion based on densely-connected high-resolution CNN and hybrid transformer. Neural Computing and Applications, 1-21.
[2]. Qiu Y 2020. Clustering Analysis for Silent Telecom Customers Based on K-means++. In 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC) (Vol. 1, pp. 1023-1027). IEEE.
[3]. Valen J 2022. Quantifying uncertainty in machine learning classifiers for medical imaging. International Journal of Computer Assisted Radiology and Surgery, 17(4), 711-718.
[4]. Bacchi S 2022. Machine learning in the prediction of medical inpatient length of stay. Internal medicine journal, 52(2), 176-185.
[5]. Ahmed U 2022. Prediction of diabetes empowered with fused machine learning. IEEE Access, 10, 8529-8538.
[6]. Kayalibay B 2017 CNN-based segmentation of medical imaging data. arXiv preprint arXiv:1701.03056.
[7]. Chen J X 2016 The evolution of computing: AlphaGo. Computing in Science & Engineering, 18(4), 4-7
[8]. Holcomb S D et al. 2018 Overview on deepmind and its alphago zero ai. In Proceedings of the 2018 international conference on big data and education (pp. 67-71).
[9]. Perez L D et al. 2016 General video game ai: Competition, challenges and opportunities. In Thirtieth AAAI conference on artificial intelligence.
[10]. Bakkes S 2009 Rapid and reliable adaptation of video game AI. IEEE Transactions on Computational Intelligence and AI in Games, 1(2), 93-104.