1. Introduction

As an important precious metal, the price of gold is highly volatile and uncertain as it is affected by the economic and political situation in the global market. Therefore, forecasting the price of gold is of great significance to investors, policy makers and economists [1]. In the past decades, many scholars and institutions have studied and forecasted the price of gold using time series algorithms.

Time series analysis is a common statistical method used to forecast values or trends at future points in time. It is based on historical data and predicts future trends by looking for patterns and relationships between data. Time series algorithms include ARIMA model, exponential smoothing model, neural network model etc [2,3].

ARIMA model is a widely used time series algorithm that captures the periodicity, trend and seasonality in the data.The ARIMA model consists of three parts: autoregressive (AR), differencing (I) and moving average (MA), where the AR part indicates that the current value is associated with a number of previous values, the MA part indicates that the current value is associated with a number of previous errors, and the I part indicates that the data need to be data to be differenced to remove seasonality or trend [4,5].

Exponential smoothing model is another common time series algorithm that predicts future values based on the mean and trend of historical data [6]. Exponential smoothing models are classified into various forms such as simple exponential smoothing, quadratic exponential smoothing and cubic exponential smoothing, of which simple exponential smoothing is the most common form.

Neural network model is a time series algorithm based on artificial neural networks that adaptively learns patterns and relationships in data [7]. Neural network models include various forms such as multilayer perceptron (MLP), recurrent neural network (RNN) and long short-term memory network (LSTM).

In gold stock price forecasting, time series algorithms can help investors and decision makers better understand market trends and price fluctuations. By analysing historical data, these algorithms can predict the likelihood of future price changes and provide recommendations about buying or selling stocks. In addition, time series algorithms can be used to formulate policies and plan business strategies, helping companies make more informed decisions.

Time series algorithms are a very useful tool in gold stock price forecasting. In this paper, an algorithm based on nonlinear weight decreasing PSO-SVR univariate time series forecasting is proposed for gold price forecasting, which can help investors, policy makers, and firms to understand the market trends and price fluctuations and make more informed decisions.

2. Introduction to the dataset

The dataset used in this article is from the Kaggle open source dataset available at https://www.kaggle.com/datasets/sahilwagh/gold-stock-prices. The dataset provides a comprehensive record of the daily price of gold from 19 January 2014 to 22 January 2024 The data is provided by NASDAQ and includes key financial indicators for each trading day.

The dataset consists of a date, a closing price, a volume, an opening price, a high price and a low price, with the date recording the unique date of each trading day, the closing price recording the closing price of gold on the relevant date, the volume recording the volume of gold traded on the relevant date, the opening price recording the opening price of gold on the relevant date, the high price recording the highest price of gold recorded during the trading day, and the low price recording gold on the trading day The lowest price of gold on the trading day.

3. Relevance analysis

3.1. Nonlinear Weighted Particle Swarm Algorithm

The Improved Particle Swarm Optimization (IPSO) algorithm is an improved particle swarm optimisation algorithm based on the particle swarm optimisation algorithm, which improves the algorithm's global search ability and convergence speed by introducing techniques such as nonlinear weights and adaptive learning factors.

Similar to the traditional particle swarm algorithm, IPSO also optimises the search based on the position and velocity of particles. However, IPSO adopts a nonlinear weighting approach in updating the position and velocity of particles and introduces an adaptive learning factor to adjust the search direction and step size, thus making the algorithm more flexible and efficient [8].

Specifically, IPSO multiplies the velocity and position changes of each particle respectively by a nonlinear function that decreases with the number of iterations. This nonlinear weighting approach allows the particles to explore the solution space more extensively at the beginning of the search, and to search for the optimal solution more intensively at the later stages of the search.

The improved particle swarm weights are nonlinear weights decreasing in the following two ways:

W ^d = W_start - (W_start-W_end) × ( \( \frac{d}{K} \) ) ² (1)

W ^d = W_start - (W_start - W_end) × [ \( \frac{2d}{K} \) - ( \( \frac{d}{K} \) ) ²] (2)

In addition, IPSO introduces an adaptive learning factor to adjust the search direction and step size. This enables the algorithm to find the global optimal solution quickly and not easily fall into the local optimal solution during the convergence process.IPSO is an efficient and reliable optimisation algorithm for a variety of complex nonlinear optimisation problems.

3.2. Support vector machine algorithm

Support Vector Machine (SVM) is a very effective algorithm for classification and regression. Its main idea is to separate different classes of data by finding an optimal hyperplane [9]. In classification problems, SVM finds the optimal hyperplane by maximising the boundary distance, which makes the classifier more robust and generalisable. In regression problems, SVMs find the optimal hyperplane by minimising the error. The schematic diagram of the algorithm for Support Vector Machines is shown in Figure 1.

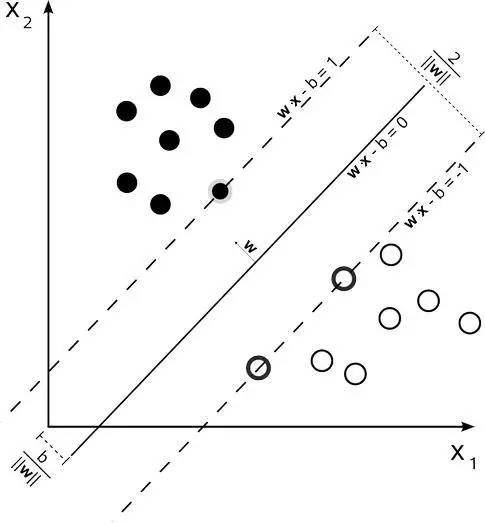
Figure 1: Support Vector Machines.

(Photo credit: Original)

The core of the SVM algorithm is the support vectors, i.e., the closest data points to the hyperplane. These support vectors determine the location and orientation of the hyperplane and play a crucial role in predicting the results.The SVM algorithm can use different types of kernel functions to deal with nonlinear problems and has good robustness and generalisation capabilities.

3.3. Support vector machine (SVM) time series algorithm based on nonlinear weighted particle swarm (IPSO) optimisation

The Support Vector Machine (SVM) time series algorithm based on Nonlinear Weighted Particle Swarm (IPSO) optimisation is a predictive model for working with time series data. The algorithm models and predicts time series by using SVM classifiers and IPSO optimisation algorithms, thereby improving the accuracy and stability of the predictions.

Specifically, the algorithm first transforms the time series data into a set of feature vectors. Then an SVM classifier is used to classify these feature vectors and find the best hyperplane for optimal classification. On this basis, the IPSO optimisation algorithm is used to adjust the parameters in the SVM classifier to further improve the accuracy and stability of the model [10]. It increases the diversity of the search space by introducing nonlinear weighting factors and can adaptively adjust the weighting factors to improve the search efficiency. This makes the algorithm better able to avoid falling into local optimal solutions and has a strong global search capability.

4. Experiments and Results

The gold stock prices from 19 January 2014 to 22 January 2024 were imported and the data set was divided in a 7:3 ratio with 70% of the data used for training and 30% for testing. The data was normalised and simultaneously transposed to fit the model, the best fit curve was plotted to extract the best parameters, and the values of R2, MAE, MBE and MAPE were calculated for the training and test sets.

Y-X scatter plot is plotted for training set predicted and true values as shown in Fig. 2 and Y-X scatter plot is plotted for test set predicted and true values as shown in Fig. 3.

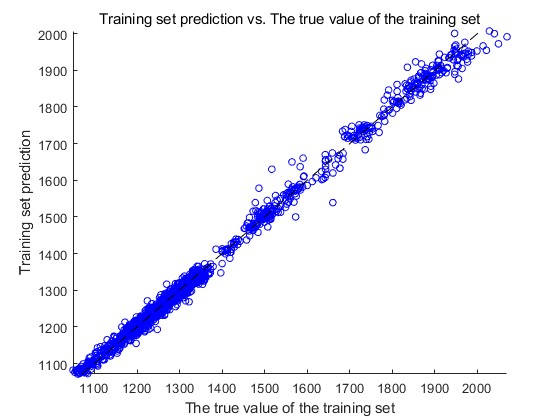
Figure 2: Y-X scatter plot.

(Photo credit: Original)

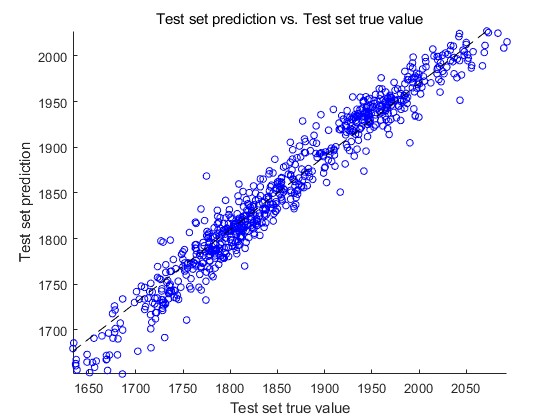
Figure 3: Y-X scatter plot.

(Photo credit: Original)

The predicted and true values of the training set are plotted on a line graph in the coordinate system as shown in Fig. 4, and the predicted and true values of the test set are plotted on a line graph in the coordinate system as shown in Fig. 5.

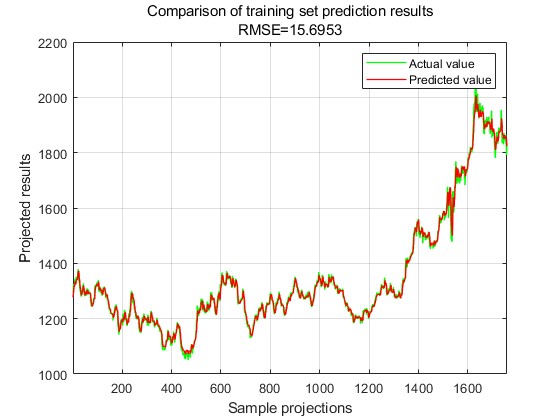
Figure 4: Training set predicted-actual value line plot.

(Photo credit: Original)

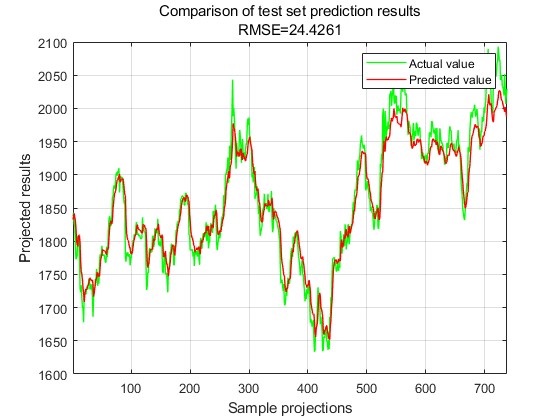
Figure 5: Test Set Predicted-Actual Line Chart.

(Photo credit: Original)

As can be seen from the predicted and true values plotted on the Y-X scatter plot and the line graph of the predicted and true values of the training set, the Support Vector Machine (SVM) time series algorithm based on Nonlinear Weighted Particle Swarm (IPSO) optimisation is able to predict the price of the gold stock very well, and the predicted and actual values of the price of the gold stock can be very close to each other in both the training set and the test set.

The values of the evaluation metrics R2, MAE, MBE and MAPE for the training and test sets are shown in Table 1.

Table 1: Indicators for model evaluation.

As can be seen from the model evaluation indexes, the values of R2, MAE, MBE and MAPE all reflect the very good prediction effect of the model, which proves that the Support Vector Machine (SVM) time series algorithm based on Nonlinear Weighted Particle Swarm (IPSO) Optimisation is able to predict the price of the gold stock very well, and the prediction results of the test set do not have a large deviation from the training set.

5. Conclusion

In this paper, an algorithm based on nonlinear weight decreasing PSO-SVR univariate time series prediction is proposed to predict the gold price, which can help investors, policy makers and enterprises to understand the market trends and price fluctuations and make more informed decisions. By plotting Y-X scatter plots and line plots of the predicted and real values of the training set, it can be found that the algorithm can predict the gold stock price well, and the predicted values are very close to the real values in both the training set and the test set. Meanwhile, the values of the model evaluation indexes R2, MAE, MBE and MAPE also reflect that the model has a good prediction effect. Therefore, the support vector machine time series algorithm based on nonlinear weighted particle swarm optimisation is an effective method to forecast gold prices. This is of great significance to investors, policy makers and enterprises, which can help them make more informed decisions and thus obtain better economic benefits.