1. Introduction

Due to the rapid economic growth and increasing number of immigrants, Hong Kong has one of the highest real estate prices in the world. At the same time, the wage index and household income are unable to keep up with the housing cost based on the GDP per capita [1]. Consequently, housing affordability has escalated into a severe social issue, affecting a significant portion of Hong Kong's population.

Despite the considerable development of PRH over the past decades, Hong Kong’s public housing scenario is still inadequate to match the demand. Over 220,000 people living in poor housing, such as cage houses, and have to wait for an average of six years for a public housing unit [2]. Therefore, an optimized allocation mechanism should be applied to maximize total satisfaction within the constraint of limited supply of PRH.

Drawing inspiration from Singapore's acclaimed public housing success, this essay explores the potential of advanced algorithms to revolutionize public housing allocation in Hong Kong. Singapore's model is renowned for its efficiency and equity, making it an exemplary reference. This study aims to glean insights from Singapore's approach, adapting its strategies to the unique context of Hong Kong. By employing computational tools and algorithms, the proposed method seeks to navigate the complexities of matching housing supply with demand. The goal is to ensure a fair and transparent allocation process, prioritizing the diverse needs and preferences of applicants. This comprehensive exploration involves a detailed examination of the historical evolution of Hong Kong's public housing system, the current challenges it faces, and some principles underpinning Singapore's effective public housing policies. By analyzing these aspects, the paper aims to propose a tailored algorithmic approach that addresses the critical issue of equitable housing allocation in Hong Kong.

2. Case Description

Allocating public housing is a crucial problem globally, and Hong Kong, one of the most populous cities, is confronted with many difficulties in this regard. The history of Hong Kong public housing can be traced back to the 1950s. By that time, a significant number of people flocked to Hong Kong because of the political turmoil in mainland China. The number of squatters increased dramatically as a result. On Christmas night of 1952, A tremendous fire broke out in Shek Kip Mei, which caused more than 50,000 people to become homeless. With the trigger of the fire, the former Hong Kong Housing Authority (HKHA) constructed multi-storey bungalows to provide shelter to mainland and fire victims and planned to build self-contained flats for low- to middle-income households. In 1957, North Point Estate, the first low-cost housing estate built by the former Housing Authority, was completed. Then, in the 60s, the government formally established a low-cost housing program and began constructing high-rise resettlement blocks [3]. After that, public housing developed significantly over the subsequent decades. According to the HKHA 2022/2023 annual report, by the end of 2023, the number of PRH households reached 805,023 while the number of PRH is 818,841.

Nowadays, to apply for PRH, a resident should meet the specific criteria. For instance, individuals must have a monthly income below $12,940HKD and a net asset below $278,000HKD [4]. Once the applicant is eligible, they must fill in and submit an application form. Then, HKHA will conduct a preliminary vetting of the applications. After then, a detailed interview will be conducted to check eligibility. When the applicant has satisfied all the eligibility criteria, the applicant will be put on a list. After all these complicated steps, HKHA will allocate the PRH by random computer batching based on priorities [5].

Nevertheless, the increase in the number of public housing is still unable to meet the demand. By the end of 2023, the average waiting time for regular applicants is 5.8 years, and there are still 129,400 applicants waiting for a PRH [6]. Since there is a severe shortage of public housing in Hong Kong, effective and fair allocation strategies are desperately needed. The lottery and wait times are the mainstays of the current allocation system, which, while straightforward, often do not adequately address the diverse needs of applicants or maximize the utility of limited housing resources. Numerous scholarly works have examined the concepts of equity and fairness in housing allocation, highlighting the significance of distributing resources in a way that is both efficient and just [7].

In response to the limitations of traditional allocation methods, there has been growing interest in the application of optimization algorithms to improve both the efficiency and fairness of public housing allocation. Optimization algorithms, such as linear programming, genetic algorithms, and multi-objective optimization, offer powerful tools for managing complex allocation problems by identifying optimal or near-optimal solutions from various possibilities [8]. Multiple objectives and limitations can be incorporated into these algorithms, enabling a more dynamic and nuanced approach to allocation that aligns more with the concepts of equality and fairness. For instance, the sequential mechanism used in Singapore enables the achievement of the maximum social utility [9].

Moreover, Singapore’s public housing scheme is one worth studying. In contrast to Hong Kong, Singapore’s Housing and Development Board (HDB) flats offer houses to more than 80% of Singaporeans [10]. People suggested that Hong Kong can learn two things from Singapore's comparison [11]. Firstly, the housing policy of Hong Kong should be more focused on catering to the housing needs of its citizens instead of depending on the fluctuation of the housing market. Secondly, Hong Kong should reinforce its land supply strategy by carrying out massive land reclamation.

In conclusion, studies have shown a significant imbalance in the current allocation of public housing in Hong Kong compared to the potential improvements in fairness and efficiency that optimization algorithms might offer. To capitalize on the benefits of these systems justly and evenly, bridging this divide requires a meticulous approach that encompasses ethical, societal, and political considerations alongside technological advancements.

2.1. Analysis of the Problems

To deal with the intricate challenges faced by the Hong Kong government in public housing allocation, the model should consider both the influencing factors and constraints. Therefore, an improved mechanism for optimizing the distribution of public housing resources is designed using ILP due to its versatility and proficiency in addressing the intricate nature of the public housing allocation problem in Hong Kong. Research has been conducted on how public housing is distributed in other countries, such as Singapore. By taking references from matching mechanisms from various regions, the author designed a simple model that optimized the overall utility while still considering fairness, as the allocation is based on priority.

2.2. Model Suggestion

The equation is illustrated below:

Variables of Equation (1):

Applicants: Let A { \( {a_{1}},{a_{2}},{a_{3}}…{a_{n}} \) } be the set that contains n number of eligible applicants waiting for a housing unit.

Housing units: Let H { \( {h_{1}},{h_{2}},{h_{3}}…{h_{n}} \) } be the set that contains n number of housing units waiting to be assigned.

Priority score: Each applicant \( {a_{i}} \) has a priority score \( {P_{i}} \) assigned by the government based on the priority schemes and other influencing factors such as waiting time. \( {P_{i}}∈\lbrace 1,10 \) }, in which 10 refers to the one that has the highest priority.

Satisfaction score: Each applicant \( {a_{i}} \) has a satisfaction score \( {S_{ij}} \) for each housing unit \( {h_{j}} \) based on their preferences. \( {S_{ij}}∈\lbrace 1,10\rbrace \) .

Decision Variables of equation (1):

\( {x_{ij}} \) is a binary variable that equals 1 if applicants \( i \) is assigned to housing unit \( j \) , and 0 otherwise.

Objective Function of equation (1):

\( Maximize\sum _{i=1}^{n}\sum _{j=1}^{m}{P_{i}}∙{S_{ij}}∙ \) (1)

The objective function aims to maximize the total satisfaction, weighted by priority, across all applicants.

Constraints in equation (2) and equation (3):

1.Applicants Allocation Constraints: Each applicant is assigned to at most one housing unit:

\( \sum _{i}{x_{ij}} ≤1, ∀i ∈A \) (2)

2.Housing Capacity Constraints: Each housing unit can accommodate a limited number of applicants.

\( \sum _{i=1}^{n}{x_{ij}}≤{C_{j}}, ∀j∈H \) (3)

2.3. Results and Improvements

To run this model, all the applicants are assigned a random priority score and a satisfaction score for each housing. Priority score is assigned by the government based on its priority schemes and other influencing factors such as waiting time and satisfaction score is also accessible through the application form and the interview during the eligibility checking. The first example data set is 100 applicants and 80 housing units with housing capacity of 1. Figure 1 shows the result of comparing the total satisfaction between random allocation and this ILP model.

Figure 1: Comparison between model (1) and random computer batching when 100 applicants and 80 housing units.

The bar chart shows that the overall utility is dramatically increased compared to the current computer batching method. Yet, this may be due to probability; hence, the model is iterated 100 times, and the results are shown in Figure 2.

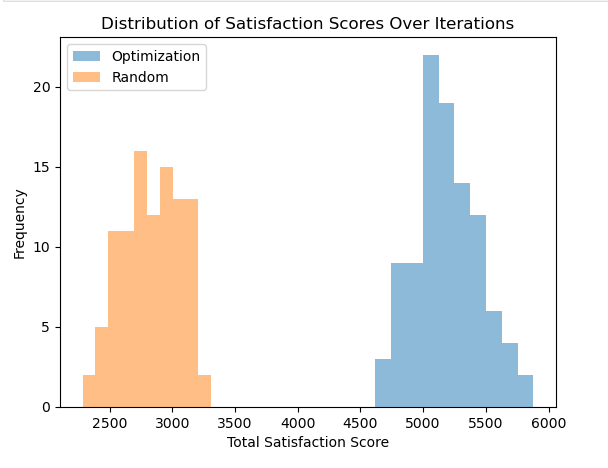
Figure 2: Results of 100-time iteration when 100 applicants and 80 housing units.

Figure 2 compares the overall satisfaction of arbitrary allocation and the ILP model when repeated 100 times. There is a vast difference between the scores obtained by these two distinct mechanisms. For random computer batching, the mean satisfaction score is about 3000, whereas the optimized model has a mean number of around 5300. In conclusion, when there are 100 applicants and 80 housing units with a housing capacity of 1, the ILP model significantly enhances the total utility.

However, the number of housing units and applicants seems unrealistic. For example, in 2023, only 13,700 PRH are assigned to the public, but there is a total of 143100 applicants. The PRH number only accounts for approximately one-tenth of the total number of applicants. Therefore, the variables should be adjusted.

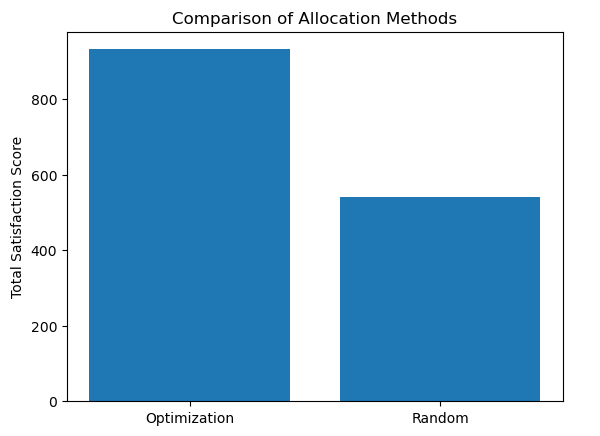
Figure 3: Comparison between model (1) and random computer batching when 100 applicants and 10 housing units.

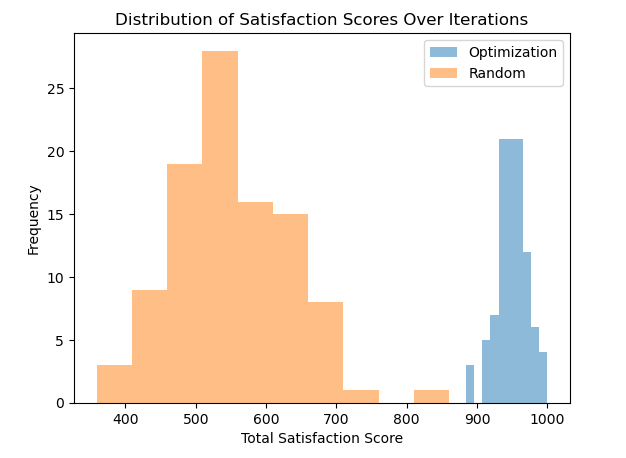
Figure 4: Results of 100-time iteration when 100 applicants and 10 housing units.

Figure 3 and Figure 4 show the result when the number of housing units is assumed to be 10 while the number of applicants remains 100 and the result of 100 times iteration, respectively. As shown in Figure 4, the total satisfaction score for random allocation seems to be discrete, while the ILP model score seems highly concentrated. In this circumstance, although the total utility score has not shown a considerable gap between the two algorithms, the mean number of the score still shows a remarkable rise when applying the optimized mechanism.

However, there is still one essential that is ignored during the matching, which is stability. No agents are inclined to stray from the allocated distribution. Some papers proposed that stability is a crucial factor in developing an effective matching mechanism [12]. To achieve this, the mechanism designed should allow agents to exchange their housing if they both will be better off. Then, a new module is added to the current model for which \( {i_{1}} \) and \( {i_{2}} \) will exchange their housings if \( {S_{{i_{1}}{j_{1}}}} \lt {S_{i{j_{2}}}} \) and \( {S_{{i_{2}}{j_{2}}}} \lt {S_{{i_{2}}{j_{1}}}} \) and \( {x_{{i_{1}}{j_{1}}}}∙{x_{{i_{2}}{j_{2}}}}≠ 0 \) .

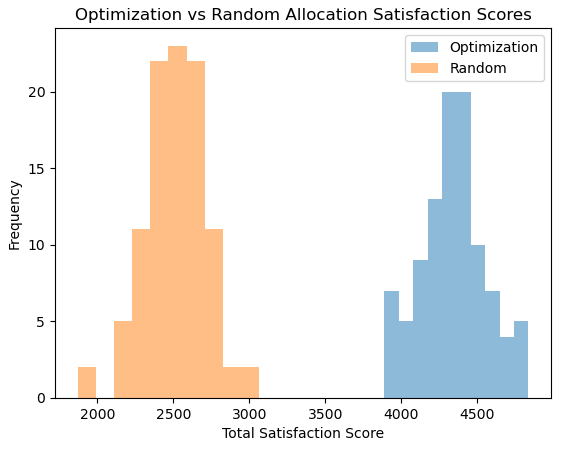
Figure 5: Iteration results of the stabilized model.

Based on the following changes to the model, the improved model has been rerun with the same variables and iteration times. Figure 5 shows the result of the enhanced model; the gap in satisfaction scores appears again. Compared to Figure 2, although the utility and priority scores differ, total satisfaction is dramatically enhanced. There is a considerable increment in the mean satisfaction score concerning the random allocation. As a result, the model change achieved stability while raising the total satisfaction relatively.

3. Conclusion

In conclusion, it is evident from the research that the current distribution of public housing is not utility-maximized and efficient. The current situation can be significantly improved by optimizing of the allocation algorithm, which dramatically enhances allocation satisfaction and stability, potentially reforming the way of housing distribution. However, merely adopting the new algorithm will not solve all the problems. Achieving the full potential of these technologies in a fair and equitable way requires careful consideration of ethical, social, and political factors alongside technological advances. Additionally, the insufficient number of public housing is the primary reason for all the current conflicts. Hence, tackling this complicated social issue requires the cooperation of multiple government policies and reforms.

The impacts of this research extended beyond academia into the practical realm of policymaking. The need for interdisciplinary approaches that combine algorithm programming intricacies with the diverse human aspects of public policy is brought out in this statement. Policymakers are thus advised to involve themselves in it and use it as a basis for coming up with an all-inclusive approach to public housing distribution, which combines efficiency with empathy.