1.Introduction

In the financial market, especially the stock market, investors consistently aim to maximize earnings while managing risks. However, the complexity and uncertainty of the financial market make achieving this goal extremely challenging. To guide decisions effectively, investors need to rely on scientific models and tools to measure and balance earnings and risks. As the financial market develops, the diversification of investment demands is also increasing. Investors are not only concerned about the level of earnings but also increasingly focus on risk control and the reasonable allocation of their assets. Therefore, an investment strategy that considers both returns and risks is essential. In 1952, American economist Harry Markowitz published an article titled “Portfolio Selection” in the Journal of Finance, which introduced the Markowitz Portfolio Theory and the Mean-Variance Model for the first time. This model is a milestone in venture capital as it marks the first application of mathematical statistics to portfolio selection, allowing for the optimal balancing of earnings and risks.

Based on the Mean-Variance Model, this paper quantifies the expected earnings and risks of an investment portfolio using mathematical methods, providing a scientific basis for investors to make decisions. It assumes that the yield rate follows a normal distribution and measures risk through variance (or standard deviation), balancing earnings and risks. It assists investors in pursuing high yields while efficiently controlling risks by constructing a portfolio of assets with different weights. At the same time, it identifies the patterns of stock market changes to accurately predict future trends. It selects a suitable number of relatively strong individual stocks and then uses a multi-objective decision-making method to analyze and optimize the portfolio. Thus, this paper holds considerable theoretical significance. In practical applications, different investors possess varying risk appetites and investment objectives. By calculating the expected returns and risks of portfolios under various weights, the optimal portfolio along the efficient frontier can be identified to ensure the effectiveness and adaptability of the portfolios. Securities investment imposes high requirements regarding the quantity, authenticity, and timeliness of information. This optimization method not only improves the scientific rigor and accuracy of investment decisions but also reduces subjectivity and bias in the investment process. Through the quantitative analysis of expected earnings and risks in the portfolio, investors can more clearly recognize the correlations and risk characteristics among different assets. This understanding helps investors better grasp market trends and investment opportunities while improving the accuracy and timeliness of their investment decisions. Therefore, this paper also holds considerable practical significance.

This paper begins with China’s securities market and employs Markowitz’s Mean-Variance Model to study how investors select portfolios that yield high returns with low risks. First, this paper reviews the historical evolution of investment theory and strategy, as well as existing research both domestically and internationally. Then, it conducts empirical research and analysis of the Mean-Variance Model applied to portfolios using historical data. Therefore, the structure of this paper is organized as follows: The first section is the introduction, which provides a detailed overview of the research background and significance of the topic, proposes the research method, and outlines the content of each section. The second part is the literature review, which examines the historical development of portfolio strategy and existing research on the Mean-Variance Model. The third section details the Mean-Variance Model and simulates data for comparison with actual historical data. In the fourth section, the mean-variance rate of returns is predicted, and the difference between the prediction accuracy and actual investment returns is analyzed to assess the practicality and applicability of the Mean-Variance Model. The fifth section summarizes the entire paper.

2.Review of Relevant Research Literature

With the continuous development of China’s stock market, stocks have occupied a considerable proportion of people’s assets. Therefore, changes in the stock market are closely related to the welfare of the population. However, China’s stock market is highly volatile, which creates significant uncertainty and risk. Consequently, investors face unprecedented opportunities and challenges. On the one hand, diversified asset classes (such as stocks, bonds, commodities, real estate, and digital currencies) offer abundant investment options, providing a wide range of choices for investors with varying risk preferences and return objectives. On the other hand, as market volatility and uncertainty increase, the performance of individual assets or markets becomes difficult to predict, and the risks associated with single investment strategies are amplified. Therefore, this paper aims to employ Markowitz’s Mean-Variance Model to help investors select investment portfolios effectively, thereby improving returns and reducing risks.

Regarding the innovation and improvement of the Mean-Variance Model, existing research has made considerable progress.

Starting from China’s securities market, Chen [1] studies stock selection based on company growth and value. On this basis, he applies multi-objective decision-making and the minimum semi-absolute deviation criterion in portfolio selection. By introducing the triangular fuzzy number, the fuzzy hierarchy algorithm with constraints is utilized to determine the weight of attributes. The TOPSIS method is used to make the weights of attributes objective and significantly reduce the computational burden of the model. Hamdi. A [2] presented a generalized MV-CVaR combinatorial optimization problem with realistic constraints. In order to solve the mixed integer quadratic model in numerous scenarios, the penalty decomposition method (PDM), which has been widely used in recent years, is employed to decompose the underlying problem into two sub-problems. With the increase of the value of K, in most cases, the CPU time will decrease.

Liu [3] improved the traditional Mean-Variance model by enhancing the established PBIL algorithm used for distribution estimation. According to the characteristics of the Mean-Variance model, he adapted PBIL into a method suitable for continuous spatial real-value coding and designed a model that considers both transaction costs and risk-free assets. Based on this improved model, a version that considers only transaction costs and only risk-free assets is derived. Xu [4] focused on the impact of capital market pressure on corporate financial asset investment. Through the construction of a hypothesis and a regression model, he demonstrated that stock liquidity significantly promotes corporate financial asset investment and that the relative return rate expressed by VAR plays a crucial role in financial asset investment, as indicated by the nature of property rights.

Xiong [5] used the adaptive varying coefficient factor model (FACE) to estimate the covariance of asset returns, and he dynamically and accurately estimated the portfolio covariance matrix while constructing a dual mean-variance management method for both the internal and overall positions of the portfolio.

GUBU. L [6] compared the performance of portfolios constructed using the classical MV model, the MVSK model, and the robust MV model, which overcomes the non-normal distribution of most stock returns in the capital market. Shi [7] reduced the problem to a constrained stochastic linear quadratic control problem with jumps, the solution of which is related to a partially coupled stochastic Riccati equation (SREs) system. Under the MV principle, Yi [8] proposed the optimal investment reinsurance strategy for these enterprises. By solving the complex partial integral differential Hamilton-Jacobi-Bellman equation (PID-HJB), he obtained the optimal investment reinsurance strategy and the corresponding value function for the insurance company. Lin [9] studied the selection of the optimal time-consistent mean-variance reinsurance investment strategy for insurers under the CEV model. By solving the corresponding HJB system, he obtained the approximate solution and the corresponding value function of the optimal reinsurance investment strategy under the compound Poisson risk model and its diffusion approximation.

The differences among investors will also have a significant impact. Yao [10] bases his research on the existing studies regarding the mechanism and effect of trader heterogeneity on stock price volatility, and, aiming to address the limitations of its inadequate characterization of heterogeneous behaviors, analyzes the influence of different traders’ investment behaviors on portfolio returns under various heterogeneous strategies. He considers the impact of rational traders, noise traders, and information-driven traders on market operations when they coexist and interact.

After reviewing the literature, it is clear that both Chinese and foreign scholars have explored and studied portfolio strategies based on mean variance and have gradually improved the predictive capability of the mean variance model on the stock market through clear investment objectives, reasonable asset allocation, diversified investments, and regular evaluations and adjustments to establish a portfolio that achieves high returns while minimizing risk. Given China’s unique national conditions and system, research in this area has started relatively late among Chinese scholars. Therefore, this paper aims to further improve the mean variance model based on the research of domestic and foreign scholars and enhance China’s capital market.

3.Research Design

In this paper, the domestic A-share market from October 29, 2021, to March 28, 2022, is chosen as the research subject. After removing samples with missing data, ten stocks from the same period are randomly selected, yielding a total of 1,010 valid samples. Data source: Kaggle library. Explained variables: expected return and overall risk. Explanatory variable: The investment weight of each stock, denoted as Wp, is set to study the problem of different stock portfolio strategies and to improve the comparability among different stocks. Control variable: growth rate.

The mean-variance model calculates the daily growth rate of each stock using the original data, yielding the average growth rate for the ten stocks and the transposed matrix e. Then, the covariance of the ten stocks is calculated to obtain the covariance matrix V, and the inverse covariance matrix V-1 is computed, along with the parameter vectors g and h.

The following model is constructed:

\( A={1^{T}}{V^{-1}}e \)(1)

\( B={e^{T}}{V^{-1}}e \)(2)

\( C={1^{T}}{V^{-1}}e \)(3)

\( D=BC-{A^{2}} \)(4)

g\( =\frac{1}{D}[B({V^{-1}}e)-A({V^{-1}}e)] \)(5)

h\( =\frac{1}{D}[C({V^{-1}}e)-A({V^{-1}}1)] \)(6)

\( {W_{p}}=g+hE[\widetilde{{r_{p}}}] \)(7)

Ten stocks were replaced for analysis. The covariance matrix and the inverse matrix were calculated, yielding the results A = -13.385, B = 0.087, C = 14,939.194, and D = 1,125.929, along with the parameter vectors g and h.

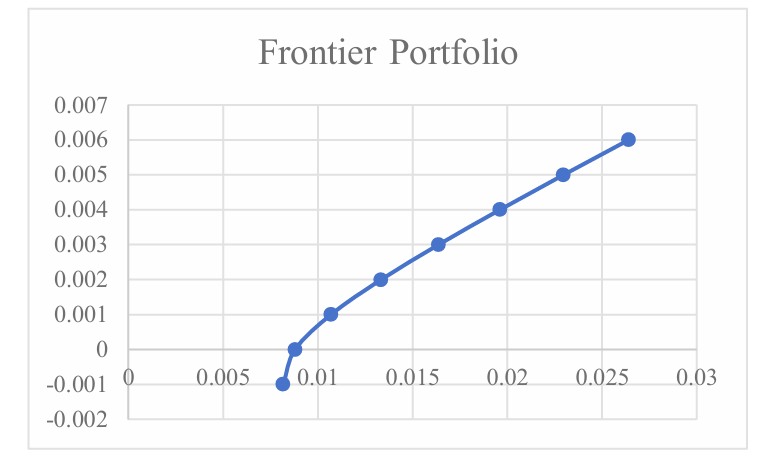
Figure 1: Frontier portfolio based on the above data.

Taking E=0.004 as an example, the weights of the ten stocks are 5.01%, -11.66%, -22.55%, 16.32%, 22.52%, 26.05%, 85.71%, -29.96%, -3.80%, and 12.36%. The second, third, eighth, and ninth stocks, which have negative weights, are removed, and the weights of the remaining six stocks are recalculated.

It can be obtained that A1=-13.615, B1=0.066, C1=14275.972, D1=759.195, and the parameter vectors g1 and h1 are calculated. Using E=0.004 again, the weights of the six stocks are -2.14%, 20.01%, 26.22%, 28.41%, 20.34%, and 7.16%, respectively. The first stock with a negative weight is removed, and the weights of the remaining five stocks are recalculated.

It can be obtained that A2=-13.315, B2=0.066, C2=14035.949, D2=746.204, and the vector parameters g2 and h2 are calculated. The weights of the five stocks are 19.67%, 26.07%, 27.15%, 19.82%, and 7.29%, with a variance of 0.000531876 and a standard deviation of 0.02306244. Thus, the optimal weight combination of these ten stocks can be obtained under the expected return rate of 0.004.

4.Discussion

As can be seen from the Figure 1 of the frontier curve function, the apex of the hyperbola is below the horizontal axis. This indicates that, under the same expected return rate, the standard deviation of the ten stocks increases correspondingly, meaning that investors need to bear greater risks. Therefore, when the model is applied in an unfavorable market environment, the risk will also increase.

When selecting target stocks in the market, a greater difference between the selected stocks results in a larger discrepancy in the weight ratios. Consequently, there is a higher likelihood that the weight ratio will be negative in the recalculation, leading to more stocks being discarded and a smaller number of stocks remaining for the final investment. Therefore, it is essential to select target investment stocks reasonably according to specific market conditions.

Since stocks can only be purchased in whole numbers, and since the function may take on all real numbers, this paper discusses both the real number optimization problem and the integer optimization problem. Given that the unit price of each stock is generally fixed, if the amount of investment is small, a greater proportion of each share relative to the total number of stocks results in a higher weight. Consequently, even a slight adjustment will have a significant impact on the weights of other stocks, necessitating the adoption of an integer optimization strategy, which fine-tunes the real number approach, leading to differences between the two optimization strategies. However, when the amount of investment is large, the proportion of each share decreases accordingly. As the investment amount increases, the impact of changes in a single stock diminishes, and the changes in the weights of each stock become progressively smaller. Calculations accurate to two decimal places reveal that the impact is nearly negligible. Therefore, the function curve of the frontier combination can be approximated as a hyperbola. As the expected investment increases, the difference between the real number optimization strategy and the integer optimization strategy diminishes.

In this paper, the real number optimization strategy is adopted to allow for the selection of any investment. Compared to the integer optimization strategy, it has a wider scope of application and eliminates the need for complex calculations to convert the real number optimization into integer optimization. This approach reduces computational pressure and simplifies the model. Consequently, the applicability and superiority of the real number optimization strategy utilized in this paper are evident.

5.Conclusion

This paper addresses a double-objective optimization problem that balances benefits and risks. The mean-variance model is employed to achieve optimal multi-objective outcomes regarding benefits and risks. The prices of ten stocks in China’s A-share market from 2021 to 2022 are selected as samples. These stocks exhibit characteristics such as a short time span, high sensitivity of investors to returns in the stock market environment, and significant differences in risk preferences. Consequently, the mean-variance model controlling for expected returns is utilized, leading to the following conclusions:

Given the substantial investment quota and the large number of target stocks, the change in a single stock has minimal impact on the weight ratios of other stocks. This paper adopts a real number optimization strategy to continue investing in an adverse market environment. Under the same expected return rate, the standard deviation of the stock investment weight portfolio increases, resulting in a corresponding rise in risk. The greater the degree of differentiation among the selected target stocks, the larger the difference in the weight ratios of each stock, and the fewer the number of stocks in the remaining optimal frontier portfolio after screening. Investors should make rational expectations regarding returns and risks based on the specific market situation and select suitable alternative stocks to achieve maximum returns and minimum risks.