1. Introduction

Pairs trading was first proposed by Gerry Bamberger and put into practice by Nunzio Tartaglia at Morgan Stanley in the 1980s. It is a market-neutral strategy that identifies similar stock pairs, tracks their price movements, and trades on the spread, i.e., differences. A short position entails selling a stock that is not owned, anticipating that its price will decline. That is done by borrowing shares from a broker, selling them on the market, and then repurchasing them later at a lower price to give back to the lender. A long position is when one buys a stock with the expectation that its price will rise over time and then sells it at a higher price to pocket the difference. Generally, the strategy allows traders to benefit from nearly any market condition, such as uptrend or downtrend movements. The study by Rad, Low, and Faff demonstrates that pairs trading strategies based on distance and cointegration methods show higher economic and risk-adjusted performance during market crises [1]. These strategies can be valuable in investment portfolios during turbulent times. However, it is not risk-free, and divergence might cause losses. Divergence can result from short-term changes in supply and demand, large transactions in one security, significant news impacting one of the companies, or macroeconomic changes. As a result, the strategy demands experience and skills in taking advantage of opportunities and making decisions at the right time.

Traditional approaches for pairing pairs are mainly based on statistical techniques, such as cointegration, correlation analysis, distance, etc. Cointegration is the property that demonstrates there is a long-term connection between two non-stationary time series, even when their prices may change randomly. When a cointegration relationship is found, the pair is seen as a good candidate for pairs trading. Correlation analysis looks for pairs of assets whose price movements are related over a certain time. Pairs are sometimes chosen based on their similarity in industry or sector to ensure that genuine components dictate the relationship. The principle of the strategy is simple: if one stock rises when the other falls, the strategy would short the overperforming stock and long on the underperforming one, since investors anticipate the price gap, or "spread" between the two to return to normal levels. Pairs trading has changed over time with better technology and analysis methods. In the past, the strategy mostly used manual analysis and rudimentary statistical methods. However, with the rise of technology, pairs trading has become more advanced, where using high-frequency data, real-time analysis, and more complex risk management systems are possible. As computational power has increased, traders are now able to back test pairs trading strategies on vast datasets, identify pairs with strong historical correlations, and optimize entry and exit points in a more automated manner.

Gatev, Goetzmann, and Rouwenhorst analyze a hedge fund equity trading strategy rooted in the notion of co-integrated prices within a relatively efficient market, known on Wall Street as pairs trading. This strategy involves identifying pairs of stocks that are close substitutes based on a minimum distance metric in price space. Their findings indicate that trading appropriately selected stock pairs can generate profits that remain resilient even when accounting for conservative transaction cost estimates [2]. Furthermore, extensive analysis of the U.S. stock market and 34 international markets shows that trading pairs based exclusively on information about past prices consistently generate profits [3]. We are motivated by the results and will build a model based on historical information to check its performance in generating profits and explore potential relationships with returns in this research. However, the theory of market efficiency opposes the profitability of the model. In its weak form, the theory assumes that a stock's value already incorporates all past trading information, implying that historical data cannot reliably predict future price movements. A key theoretical implication of this idea is that no trading strategies based on historical data should consistently generate returns significantly exceeding those of a benchmark portfolio [4]. To address this debate, this study seeks to empirically evaluate the profitability of pairs trading strategies by examining a large sample of securities across different market conditions. In addition, it also aims to explore the potential relationships between these strategies and key market variables such as volatility and return correlation.

Recent studies have explored high-frequency pairs trading strategies based on the Ornstein-Ulhenbeck process with jump-diffusion and regime-switching in the energy futures market [5]. The main contribution of this study is the development of a comprehensive framework based on traditional pairs trading to analyze the performance of pairs trading strategies across multiple assets. This study expands the scope to include a diverse set of securities and focuses on long-term profitability and robustness. Various statistical techniques will be employed, including correlation, Z-score tests, and linear regression models, to identify promising pairs and assess their performances. Moreover, our analysis will incorporate the effects of transaction costs and risk management strategies, providing a more holistic understanding of how pairs trading can be applied in practice. By testing the profitability of pairs trading against the efficient market hypothesis, this research aims to provide new insights into the strategy’s potential and its broader implications in the real world.

The remainder of the paper is organized as follows: Section 2 discusses procedures for implementing pairs trading strategies, including pair selection, lookback data computation, and Z-score approaches. Section 3 describes the result of expanding the number of pairs to 5000 and the consequences of applying a linear regression model. Section 4 analyzes the outcome of a specific portfolio, assuming transaction costs are involved. Section 5 simply concludes the paper.

2. Methodology for pairs trading

2.1. Stock pair selection

The first step in constructing a pairs trading strategy is to identify suitable pairs of stocks, and many different criteria have been applied to form a partner. Traditionally, the most common approach has been to minimize the sum of squared differences in price movements between two stocks. However, Do and Faff show that the traditional pair-matching criterion of minimizing the sum of squared differences is insufficient. They add two additional metrics, such as industry homogeneity and the frequency of historical reversal in the price spread, to enhance trading profits [6]. In their approach, industry homogeneity ensures that the selected stocks belong to the same sector or industry, while the frequency of historical reversals refers to the regularity with which the price spread between the two stocks reverts to its mean. Involving these two factors creates opportunities for profitable trades and cements the strategy's robustness.

In addition, metrics like return correlation offer significant advantages in evaluating pairs trading opportunities. Stocks with a high return correlation tend to move in a similar pattern, which makes them more likely to have profitable trades when one stock is undervalued compared to the other. This is particularly useful in constructing a pairs trading model, as a high return correlation often leads to greater consistency in the mean-reversion behavior of the spread. Studies by Brunetti and De Luca show that metrics like return correlation offer distinguished profitability per unit of risk. The results hold even after considering commissions, stricter cut rules, and market impact, with the log-prices correlation remaining statistically significant [7]. The key concept here is to choose a pair of stocks that are close substitutes. For instance, Pepsi and Coke are well-known competitors, and because of their close competition and similar market conditions, pairs trading is often successful with this pair.

In this case, we choose a pair of stocks within the same industry to start a preliminary model since we expect the stocks in the same sector to be close substitutes and have a relatively high return correlation. Global Industry Classification Standard (GICS) is a framework that helps investors understand companies' core business and activities worldwide. There are eleven primary sectors: energy, material, utilities, health care, etc. Below the basic sectors, more branches classify companies into distinct industries and sub-industries. This ensures the selected pairs have underlying similarities, which is essential for the success of the pairs trading strategy. Within each industry group, stock pairs can be selected using various criteria. A straightforward approach involves random selection, ensuring a wide variety of pairs. In this section, a pair of Chinese stocks 600603 and 600606 is chosen for our preliminary analysis, where both stocks come from equity real estate investment trusts. Then, a 20-day dataset from 28 May to 24 June 2020 is extracted. By focusing on a relatively short time window for this preliminary analysis, we aim to observe the basic dynamics of the pair and test the hypothesis that the stock prices will exhibit mean-reverting behavior. This initial selection of stocks from this pair serves as a starting point for our analysis, and further refinement of the model will be carried out by experimenting with additional pairs and considering a broader range of market conditions.

2.2. Return series calculation

Once a pair is selected, the price series for each stock is processed to compute returns across multiple time frequencies: 1-minute, 5-minute, and 10-minute. This step involves resampling the original minute-level data to derive returns at the specified intervals. The minute return is calculated by the formula (P_n+1 - P_n) / P_n where P_n is the price at time n and P_n+1 is the price at time n+1. Similarly, we can compute the 5-minute return and 10-minute return using the corresponding time intervals. By resampling the data and calculating returns at different time frequencies, we can better understand how price changes over time and trading opportunities across multiple time horizons.

To ensure comparability, the price series of both stocks should be normalized. In our research, normalization is achieved by dividing each stock’s price by its initial value at the start of the sample period, setting the normalized price to 1 at the starting point. A normalized price series provides a clear visualization of the relative movement of the two stocks over time and adjusts the spread correspondingly. The difference between the normalized price series is then calculated, and its behavior is analyzed further by calculating the mean and standard deviation in the sample period. These metrics are instrumental in computing Z-score values for the trading strategy, which helps us to determine when to enter or exit the stock market. Therefore, this works as a lookback model to forecast the spread trend in other trading periods and anticipate when the spread may revert to its mean. In Figure 1, we observe that the price of 600606 is higher most of the time, and the normalized price series shows an approximately constant spread from the 2500th minute to the 4250th minute. In addition, this model's standard deviation is 0.0157, and the mean is -0.0147.

Figure 1: The red line represents the normalized price trend of 600606 stock, and the blue line is the normalized price trend of 600603 stock, where each is adjusted to its initial price, and the timeline is 10 days

The study by Wang et al. examines various correlation measures in the context of pairs trading and they find that different correlation measures exhibit significant variations in terms of both return and risk. Pearson strategies have higher mean cumulative returns than Maronna and Combined but higher standard deviations than Combined [8]. In our research, Pearson correlation on the return series will be used since it is widely known and easier to interpret. Thus, the resulting return correlation is a statistical measure that quantifies the relationship between the price movements of two assets over a specific period. It is derived by calculating the correlation of their return series, which represents the percentage change in price from one period to the next. A correlation value of +1 indicates that the stocks move in perfect tandem. Conversely, a correlation of -1 suggests that the two assets move in opposite directions. In this section, we track every minute of return to get a return correlation of 0.0771. The consequence looks small since it is hard for prices to follow the same pattern every minute. However, the 5-minute return correlation is 0.1930, and the 10-minute return correlation is 0.2975, demonstrating that the overall prices are associated.

2.3. Profit and loss calculation using Z-score strategy

We filter another 10-day dataset as our trading window where the pairs trading method is applied. The core principle is that when the price spread between the two assets deviates significantly from the mean, the model enters the market and forecasts the difference to return to its average. The strategy is based on the Z-score of the spread, which quantifies its deviation from historical norms. The Z-score is calculated as (1):

\( {Z_{t}} = \frac{Sprea{d_{t}} - {μ_{spread}}}{{σ_{spread}}} \) (1)

where Z_t is the Z-score at time t; Spread_t is the spread at time t; µ_spread is the mean spread of the lookback model and \( {σ_{spread}} \) is the standard deviation of the lookback model.

The strategy follows a rule-based approach for entering and exiting trades. A position is opened when either Z_t ≥ 1 or Z_t ≤ -1. If it is the first case, the strategy will short stock 1 and long stock 2. Otherwise, it will long stock 1 and short stock 2. A position is closed when either Z_t ≤ 0.5 or Z_t ≥ -0.5. If it is the former one, the model will close the short on stock 1 and the long on stock 2, otherwise close the long on stock 1 and the short on stock 2. There are many distinct choices of entry and exit thresholds where every combination causes a completely different result. Zeng and Lee want to find the best thresholds to optimize the expected return per unit of time in three cases [9]. However, for simplicity, we manually fix entry and exit thresholds to check the performance of the pairs trading strategy under this situation. Once a trade is initiated, the state of position is recorded according to the sign of the Z-score, and equal amounts of capital (e.g., $500 each) are allocated to the long and short positions. When the trade ends, profit and loss (PNL) are calculated using the difference between the entry and exit prices times the units of the shares bought. In the last 10 minutes, all shares are compulsorily sold at the market price, even though the Z-score does not meet the exit threshold. As a result, a large divergence may generate significant losses. In our model, we use the technique called "Equally Weighted", where the amount invested in each stock of a pair is equal. However, Ramos-Requena, Trinidad-Segovia, and Sánchez-Granero suggest different methods for determining the weight factor in pairs trading, including approaches based on volatility, return correlation, or minimal distance of the log prices [10]. Therefore, we may get a more satisfactory result by using their methods in our model.

The position value starts from the original value of the investment, and it accumulates every minute by adding the PNL of every minute. When the position value is less than 75% of the initial capital value, a scheme called "margin call" is activated to sell all the equity at the current market price and return the capital borrowed. A margin call occurs as the equity in the trading account falls below the required maintenance margin. This typically happens in leveraged trading, and continuous losses would put the broker's loaned funds at risk. In this case, the system cuts losses in time and protects investors from significant losses that could jeopardize their ability to trade in the future. In this model, we assume there is no other trading once a margin call occurs due to a lack of confidence in the strategy. Minute return is calculated by (current position value - last minute position value) / last minute position value. Therefore, we can generate a return series in trading minutes, which is essential for evaluating the strategy's performance.

Sharpe ratio is a term that compares the return of an investment with its risk. It's a mathematical expression of the insight that excess returns over a while may signify more volatility and risk rather than investing skill. Sharpe ratio is a method that measures risk-adjusted relative returns. The formula is given by

\( Sharpe Ratio = \frac{{R_{p}} - {R_{f}}}{{σ_{p}}} \) (2)

\( Annualized Sharpe Ratio = \frac{({R_{p}} - {R_{f}})×252×390}{{σ_{p}}×\sqrt[]{252×390}} \) (3)

where R_p is the portfolio return, R_f is the risk-free rate, and \( {σ_{p}} \) is the standard deviation of the portfolio's excess return. The annualized formula considers that a trading day has 390 trading minutes, and a trading year contains 252 trading days. In this paper, annualized Sharpe ratio is used to compare each pair’s performance.

In Figure 2, it is obvious that there are three trades during the whole period and the last trade is closed at the last 10 minutes since the trend does not cross the exit threshold after entering the market. The first trade occurs at the 6th minute and closes at the 24th minute, which gives a profit of 6.6515. This trade lasts for only a few minutes since the Z-score rapidly decreases to less than 0.5. The other two trades generate benefits of 5.0405 and 19.7479, respectively. Surprisingly, the last trade still makes some profits, where the cause is that the percentage of decrease in the short leg is greater than the growth in the long leg. Fortunately, the position value in this pair goes up and does not reach the level of triggering a margin call. Overall, the total PNL is 31.44, and we get an actual return of 0.03144 (total PNL / investment). To compute the Sharpe ratio, non-trade minutes are manually excluded, and only traded minutes are combined to form a return series. The mean of return is 1.6817e-5, and the standard deviation is 9.7978e-4. In this analysis, the risk-free rate is zero; therefore, the annualized Sharpe ratio is 5.3810. The ratio is quite high, meaning the investment is worthwhile given the risks.

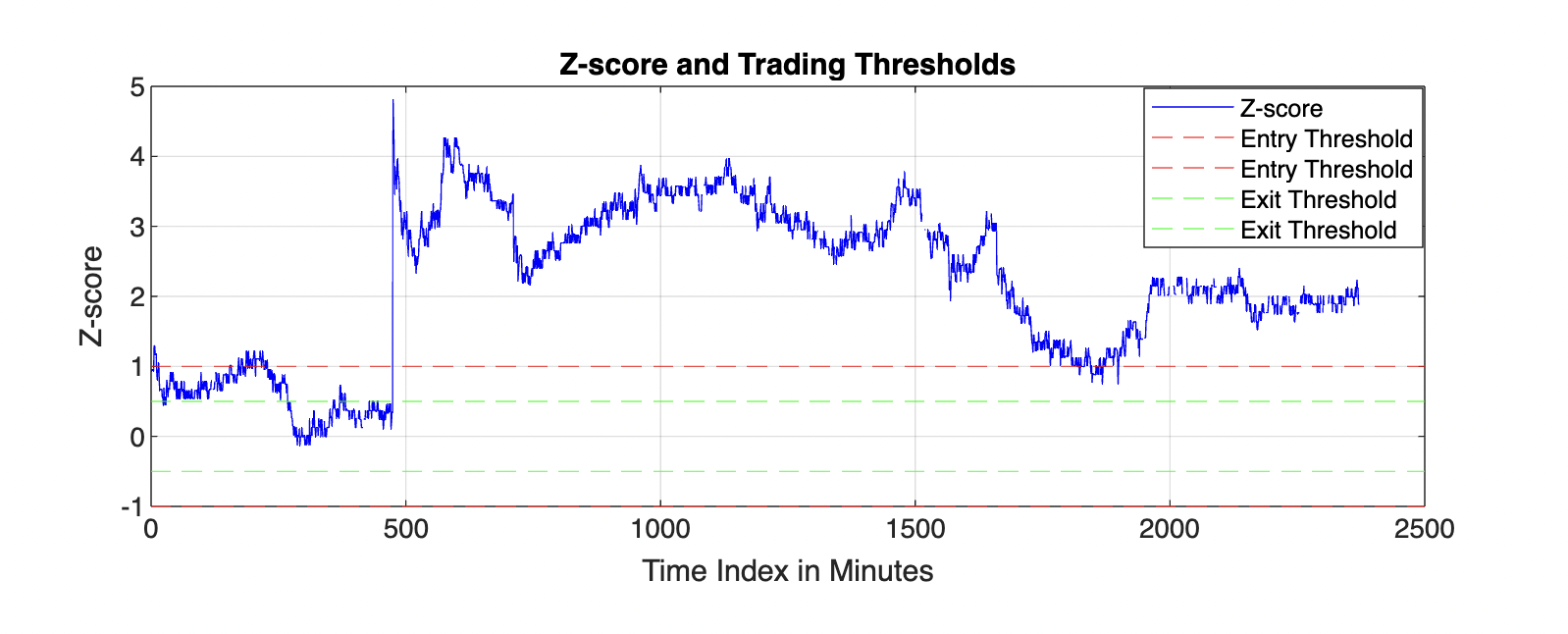
Figure 2: The red lines are entry thresholds, and the green lines are exit thresholds. A trade is finished when the Z-score either surpasses +1 and then decreases to +0.5 or drops below -1 and rebounds to -0.5

3. Pair expansion and regression analysis

The process is expanded to generate 5,000 pairs across various industries, and the timeline is one year. For each pair, performance metrics such as actual return and Sharpe ratio are calculated. In Bowen and Hutchinson's study, they explore the relationship between excess returns and market risk, size risk, value risk, momentum risk, and reversal risk by using a five-factor linear model [11]. Following this idea, the two performance metrics serve as left-hand-side (LHS) variables in a regression analysis, while lookback period statistics (e.g., return correlation, standard deviation) serve as right-hand-side (RHS) variables. The regression identifies relationships between pair features and their performance, revealing which features predict profitability.

To guarantee the preciseness of the research, we filter out the pairs whose timeline does not reach a year, and only approximately 3370 pairs of stocks are left over. The mean actual return of 0.04660 for those pairs indicates modest overall profitability. The 5th percentile is -0.3152, showing that the bottom 5% of pairs result in significant losses, emphasizing the need for robust risk management. The consequence meets our expectations as most of those pairs trigger the margin call in the trading. The positive median value demonstrates that over half of the pairs yield profitable outcomes. The 95th percentile of 0.5073 represents the most successful pairs, showcasing the strategy's potential for high returns. In terms of the Sharpe ratio, the median of 0.5834 suggests that half of the trades deliver acceptable risk-adjusted returns. However, the mean Sharpe ratio is -0.2084, which reflects the dominance of negative risk-adjusted returns, even though more pairs have positive risk-adjusted returns. The variability in Sharpe ratios underscores the importance of optimizing trade entry criteria to maximize consistent profitability while avoiding risk-heavy scenarios.

In this study, linear regression models are employed to analyze the relationship between performance measures (actual returns and Sharpe ratios) and two key independent variables, the standard deviation of spread and return correlation. Three distinct time intervals for return correlation are analyzed, each in its model. In Table 1, we know that models on actual returns have a weak explanatory power, with R-squared values around 0.02, indicating that the predictors explain only 2% of the variance in actual returns. Lookback standard deviations are consistently significant (p<0.001) across such models, showing a negative relationship with actual returns. Minute return correlation is insignificant, but the 5-minute return correlation and 10-minute return correlation show significant positive relationships with actual returns. The R-squared values of around 0.5% for Sharpe ratio models indicate limited explanatory power. The standard deviation of spread is still a significant predictor, which is negatively associated with Sharpe ratios in all models. Return correlation variables are largely insignificant, with only the 10-minute return correlation showing a weak positive association with our response. The above results highlight the detrimental impact of high spread variability on returns and Sharpe ratios, whereas the influence of return correlation is ambiguous. In addition, a larger interval of return correlation tends to be more related to our responses.

Table 1: Summaries of linear regression models. 'StdSpread' stands for the standard deviation of spread, and the suffix in 'ReturnCorrelation5' indicates that the return correlation is calculated over a 5-minute interval, following the same logic as "ReturnCorrelation10"

Pairs are then sorted into 5x5 bins based on their lookback correlation and standard deviation. The average return of each bin is analyzed to identify bins with superior performance. This double-sorting process helps isolate subsamples of trades with the highest potential profitability. The result in Table 2 reflects that pairs in bins with low standard deviations are profitable since bins in 'Std1', 'Std2', and 'Std3' have positive average returns. By contrast, bins in 'Std4' and 'Std5' show some negative average returns, especially for those in 'Std5'. In addition, the table shows that a lower standard deviation causes a higher average return as bins in the first row tend to be more beneficial. Thus, the lookback standard deviation is strongly associated with the profitability of pairs in our model. On the other hand, we cannot find a general pattern regarding the impact of return correlation on the average return. Some rows present a positive relationship between the average return and return correlation, but there are obvious violations that cannot be explained by the return correlation. As a result, the return correlation may influence the average return to some extent. The consequence aligns with our linear regression analysis, and the bin with the lowest standard deviation and the biggest return correlation is chosen for investigating. This bin has an average return of 0.1280, and its return correlation satisfies our previous assumption. Hence, we expect it to have an outstanding performance.

Table 2: The table summarizes the average return and number of pairs in each bin. 0.0745 / 77 means that there are 77 pairs in the bin with Corr1 and Std1, and the average return in this bin is 0.0745. The return correlation increases as the suffix number in 'Corr' increases (e.g., Corr5 represents a higher correlation than Corr1), following the same logic as 'Std'

4. Portfolio construction and trading costs

4.1. Portfolio performance

Using the identified high-performance pairs, we can construct a portfolio return. In Huck and Afawubo's study, the portfolio's excess return is initially calculated daily as the average excess return of all pairs (with an equal-weighted portfolio and at least 10 pairs) that are opened on a given day across the entire portfolio [12]. Following this idea, the portfolio return series is computed by aggregating the weighted returns of individual trades over time for the selected pairs. In this research, every trade has the same amount of investment and the same weight. As a result, we simply take the average on the total minute returns to get our portfolio minute return. This series is analyzed to calculate key performance metrics: annualized standard deviation, the portfolio’s volatility scaled to a yearly basis; Sharpe ratio, the risk-adjusted return; maximum drawdown, the percentage of the largest observed loss from a peak to a trough; skewness, a measure of the asymmetry of the probability distribution about its mean; Kurtosis, a characteristic of the tail of the return distribution.

The annualized volatility of 4% is low, indicating a stable trading strategy with minimal fluctuations in returns. Low volatility is desirable in risk-averse strategies as it implies consistent performance with reduced exposure to large losses. The Sharpe ratio of 6.09 is remarkably high. This value implies that the strategy generates a significant amount of return per unit of risk. A Sharpe ratio above 2 is considered excellent in most financial contexts, so this performance is extraordinary. The exceptional Sharpe ratio could be attributed to low volatility and positive return. However, the negative skewness of return distributions may lead to incorrect conclusions about Sharpe ratios [13]. In this case, we need to authenticate the value of skewness. Furthermore, as an absolute measure, the Sharpe ratio does not compare performance to a benchmark and treats the portfolio’s performance similarly to the market's performance. It is most useful for investors with a single fund, as it considers total risk, and is not easily applied when aggregating multiple portfolios due to covariance effects between volatilities [14]. As a result, the Sharpe ratio may not be reliable, but we can still treat it as a reference of goodness.

The maximum drawdown is 1.88%, which reflects the largest peak-to-trough loss adjusted to the peak during the evaluation period. This drawdown demonstrates the robustness of the portfolio return, and low drawdowns are preferred as they reduce psychological stress and recovery time. Skewness is a term that measures how many standard deviations separate the mean and median. The skewness of 4.07 represents that the distribution of returns has a significant positive skew, meaning returns are tilted towards higher positive values. The positive value of skewness reassures the doubts about the Sharpe ratio. The extremely high kurtosis value of 159.58 suggests a heavy-tailed distribution of returns, meaning that the strategy experiences occasional extreme returns (both gains and losses). While high kurtosis might raise concerns about the potential for rare but severe drawdowns, the low maximum drawdown mitigates these fears. In addition, the distribution with high kurtosis is also called leptokurtic, which is fat-tailed and has a relatively higher frequency of outliers.

Portfolio values are plotted to provide a visual representation of the portfolio's performance. From the bin sort result, the average return for this bin is positive, and we anticipate seeing an upward trend. In Figure 3, the position starts from 1000, which is our initial investment, and accumulates every minute. The final position value is approximately 1153, indicating a profit of 153 in the whole trading year. As a result, we are convinced that the pairs trading strategy has an outstanding performance in this section.

Figure 3: A plot of the portfolio value over one year. Portfolio value starts from 1000 and accumulates every minute return

4.2. Incorporating trading costs

The study by Bowen, Hutchinson, and O'Sullivan highlights the significant sensitivity of returns to transaction costs, particularly when using a more frequent trading trigger. Additionally, it demonstrates that the returns are highly sensitive to execution speed, where all excess returns are wiped out if there is a delay in executing trades [15]. Do and Faff thoroughly review the expanding literature on trading costs to build a realistic series of expenses faced by institutional investors over time, including commissions, market impact, and short-selling fees. After factoring in these costs and adjusting for systematic risks, they find that the original approach by Gatev, Goetzmann, and Rouwenhorst [2] no longer remains profitable [16]. As a result, we are convinced that it is better to involve transaction costs to examine the profitability in our portfolio. Realistic trading involves costs such as stamp duty, brokerage commission, and market impact. These are incorporated into the analysis by applying round-trip costs ranging from 0.1% to 0.3%. The impact of these costs on portfolio returns is evaluated, and the break-even cost, the level at which total returns become zero, is identified. This analysis informs the feasibility of the strategy under different cost assumptions.

We impose trading costs when entering or exiting the market to see how the portfolio return would respond. The cost of 0.1% decreases the final position value to around 1120, where the overall tendency remains nearly the same. With a cost of 0.125%, the final position value is 1111, and there is no big difference between the trends. We are convinced that conservative and low transaction costs do not remarkably influence the portfolio. In contrast, we witness a prominent change when a 0.3% barrier is imposed. The graph fluctuates significantly at troughs and peaks, and the tendency is stretched vertically. The impact of the cost is that the final position value drops to 1056, and every minute return is volatile. From this result, we forecast that the Sharpe ratio decreases due to large volatility in returns, and the actual return becomes one-third of the original. In this case, we are curious about when the cumulative return comes to zero, meaning that we do not obtain any profit in a year. The break-even cost is 0.4805% where the final position value just covers the initial investment. In Figure 4, the investment experiences a long time of recession, and the value floats dramatically. Thus, the maximum drawdown must be larger, indicating an attenuated robustness of the strategy. Since our portfolio contains many pairs of stocks, the effect of transaction costs is obvious when they continuously grow.

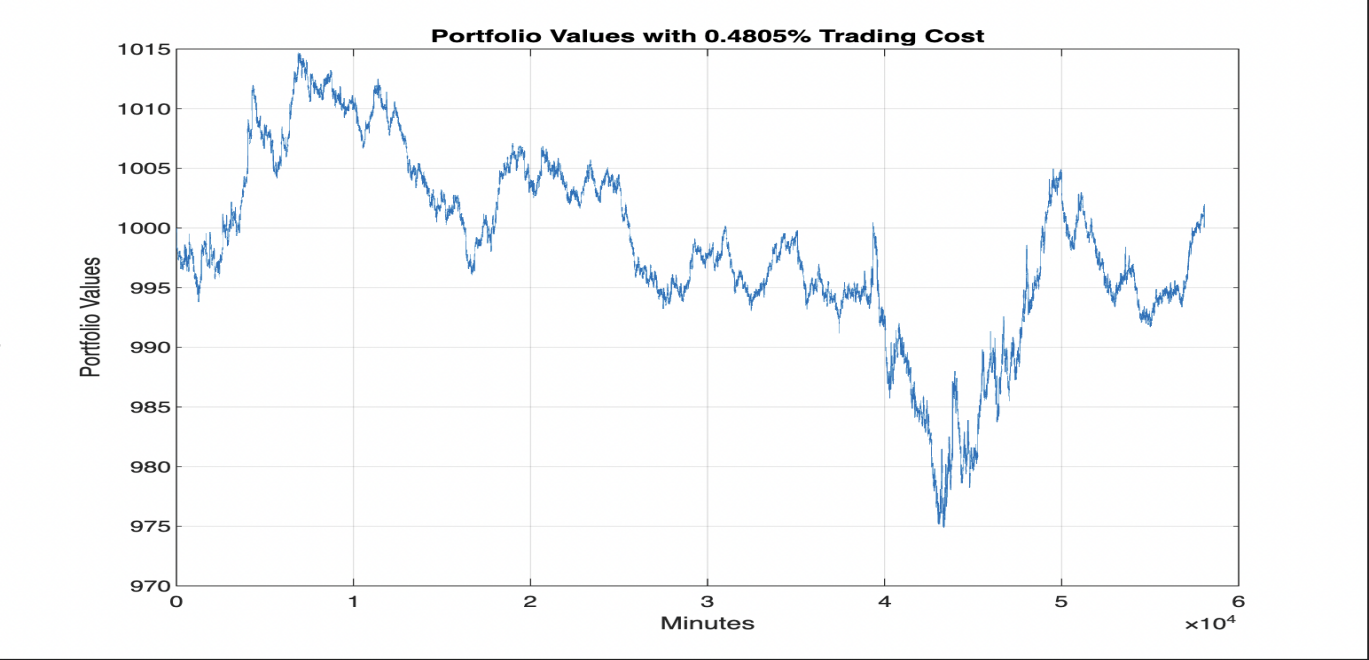
Figure 4: A plot of the position value with 0.4805% trading costs, showing the amount of trading costs required to reach the break-even condition

One of the critical aspects of trading cost analysis is liquidity constraints. Investors who deal with large orders often face higher transaction costs due to liquidity limitations, which can further inflate costs beyond standard brokerage fees. In addition, the difference between the intended and actual execution price (slippage) may vary based on factors such as order size, execution speed, and market conditions. Though our analysis assumes the market impact remains a static percentage, real markets are significantly more difficult to forecast. Another key factor influencing trading costs is the holding period and portfolio turnover. Generally, portfolio turnover is a term that measures the percentage of an investment portfolio sold out. Portfolios that are actively managed tend to have a higher turnover, which may generate more trading costs and reduce the return on the portfolio. As a result, investments with excessive turnover are often considered low-quality. Pairs trading is a strategy that requires frequent rebalancing and tends to suffer from transaction costs. By adjusting the trading frequency or employing alternative execution strategies, it may be possible to mitigate the impact of costs while maintaining strategy effectiveness. Furthermore, expanding the sensitivity analysis to include more minor cost increments, such as increasing transaction costs in 0.05% increments from 0.1% to 0.3%, could provide more details about the strategy’s resilience under varying cost conditions. By observing the graph pattern across a broader spectrum, we can better evaluate the strategy’s robustness and know when the strategy is under the exposure from transaction costs.

5. Conclusion

This methodology provides a comprehensive framework for pairs trading, encompassing four major parts. First, we choose a pair of stocks in the same GICS and record their return correlations of different intervals, spread standard deviation, and mean spread. The 10-minute return correlation is noticeable, and we expect it to obtain profits by taking advantage of abnormal divergence. Next, we apply a Z-score-based trading strategy with a particular system that stops loss to conduct our preliminary research. The result demonstrates that this pair performs well in 20 trading days with a high Sharpe ratio and positive returns.

To enrich our understanding of the strategy and get a generalized performance over a longer period, we aim to expand the model to 5000 pairs to mitigate the impact of coincidences. By applying the strategy, we get 5000 rows of data, and each row contains required information such as PNL and Sharpe ratio. Then, we filter pairs with full trading days to get around 3370 pairs of stocks. Overall, more than 50% of pairs yield profitable outcomes, and the top 5% of pairs have nearly 50% returns. However, the mean Sharpe ratio is negative, showing that negative risk-adjusted returns are dominant. Subsequently, we use a linear regression model to explore relationships between performance metrics and lookback standard deviation and lookback return correlations. With a 1% significance level, we observe that the standard deviation is statistically significant and highly associated with the return and Sharpe ratio, whereas the influence of return correlations is uncertain.

After that, we sort the pairs into 5x5 bins by return correlation and standard deviation to inspect the groups that have the potential to make profits. As a result, we point out that standard deviation reduces return, and the impact of return correlation is still ambiguous. In this case, we choose a bin with the lowest standard deviation and the highest standard deviation to investigate. We construct a portfolio by averaging minute returns for all pairs in the bin and get a portfolio return series. The Sharpe ratio for this portfolio is 6.09, meaning it is worthwhile to invest given the risks. The maximum drawdown of 1.88% eliminates the fear of frequent outliers. However, in the real world, there are commission fees, slippage, and other related costs. Therefore, we introduce trading costs to the portfolio and explore the effect of distinct trading costs on the portfolio value. Eventually, we get a break-even cost of 0.4805%, where we do not attain any profits in a year.

From the relevant literature, there are still many enhancements left to deal with to construct a better trading strategy. One key area is improving the criteria for pair selection. Our model relies on historical price relationships, but introducing more factors such as macroeconomic indicators and frequency of reversals can identify more stable pairs over time. Many papers concentrate on this part, and its importance is self-evident. Another crucial aspect is optimizing entry and exit thresholds. Adjusting these triggers based on market conditions reduces unnecessary trades. These helps mitigate transaction costs and improve the profitability of the strategy. The investment in each stock is also a vital factor that impacts return. Instead of equal weighting or fixed allocation strategies, employing dynamic investment models like mean-variance analysis could reduce drawdowns and cement the consistency of the strategy. Keshavarz Haddad and Talebi use distance, co-integration, and copula functions to compare the profitability of pairs trading in the Toronto Stock Exchange and show that the highest profitability comes from the copula method. Inspired by the research [17], we may consider using distinct methods in the future.

Apart from those improvements in the model, there are also some limitations in our data and assumptions. Our dataset collects stock information in China dating back five years, and there is a remarkable time gap to now, which may make the dataset lose its validity since the stock market constantly changes. In addition, market conditions in China are confined, and our model is solely based on stock data from China, which restricts its applicability to a broader global context. Involving stock markets across various countries in our model would enhance generality. Additionally, the assumption that the risk-free return is zero tends to lead to a higher Sharpe ratio, but the premise is not realistic since some financial institutions would pay interest to customers who deposit their money. As a result, it is necessary to adjust this assumption for a more accurate assessment of risk-adjusted returns. Another limitation is assuming that transaction costs are constant over time. Transaction costs are composed of tiny components, including brokerage fees and slippage, which fluctuate due to market conditions. Even a minor change in stock price may lead to a noticeable change in transaction costs since they are interrelated. Therefore, assuming fixed transaction costs oversimplifies real-world trading scenarios and may lead to an overestimation of profitability.

In conclusion, the analysis underscores the potential of pairs trading to deliver robust returns with controlled risks. By combining statistical techniques, the approach identifies high-potential trading opportunities and builds a robust, data-driven trading strategy. Incorporating realistic trading costs ensures the strategy’s viability in practical applications. In the introduction part, we import the theory of market efficiency and are eager to explore whether it applies to the market under various conditions. From Table 2, most bins project positive returns, even though some are minor. In addition, the regression analysis also demonstrates a significant relationship between return and the lookback standard deviation of spread. Since our strategy is based on past prices, we confirm that the weak form of the theory of market efficiency may not always be true, and pairs trading is successful while using the lookback data.