1. Introduction

Volatility is one of the most important factors in option pricing and hedging. It reflects the degree of uncertainty in profits and affects the value of options directly and the hedging strategies. With the number of financial instruments, SPY options which influenced by the SPDR S&P 500 ETF are used due to their high liquidity and the close tracking of the market. It is the reason why regard them as the suitable subject to analysis the volatility-based hedging.

There are two main ways to measure volatility: implied volatility (IV) and historical volatility (HV). On the one hand, IV is extracted form option price. And it is a symbol the market’s expectation of future volatility. ON the other hand, HV is calculated from past asset returns. It reflects the realized price fluctuation. The difference between them is regarded as the volatility risk premium (VRP), which reflects the compensation that investors demand to bear the risk of volatility. This premium is closely linked to the expected stocks returns and plays a necessary role in asset pricing [1].

Some studies emphasized the importance of adding some factors into the modeling volatility such as jumps and observable dynamics. For example, a framework for option valuation was mentioned. It includes the observable volatility and jumps factors, improving pricing accuracy and reflecting more market behaviors [2]. These cases show that the choice of volatility measure can impact the performance of hedging strategies significantly under variety of market conditions.

The main purpose of this paper is to compare hedging effects of IV and HV based hedging strategies with SPY European options. The study examines their respective performance short-term horizon as well as in different volatility regimes and it will attempt to give some relevant practical advice for volatility modelling for option hedging.

2. Literature review

2.1. Implied Volatility (IV)

IV is derived from the option price and mirrors the market’s expectation of future uncertainly. It is forward looking and responsive to investor sentiment. It usually reacting rapidly to macroeconomic news and regime shifts. The term structure of IV and its relationship with the volatility risk premium (VRP) were researched [3]. It shows that the slope of the IV curve contains predictive information about the future market conditions [3]. Their finding point out that IV incorporates both statistical expectations and market implied risk aversion [3]. A valuation framework was put forward in 2015 [2]. It combines observable volatility and jump dynamics in the framework [2]. The model figures out that option pricing and hedging strategies benefit from including IV and discontinuities, outperforming traditional approaches that rely solely on historical data [2].

2.2. Historical Volatility (HV)

HV is calculated using past asset returns. It provides a model-free estimate of actual price fluctuations. Compared to IV, HV is typically more stable and less affected by short term random noise. However, HV may ignore the sudden change of market sentiment and unable to reflect forward looking risk perception. Machine learning techniques were applied to predict realized variance [4]. The research shows that by integrating nonlinear patterns and high frequency data, model based on HV can be enhanced notably [4]. This work emphasizes the drawbacks of traditional HV estimation and the possibility for improvements driven by data.

2.3. Comparative insights: IV vs HV in hedging

Under different market regimes, whether IV is significantly better than H V in option hedging is examined. IV and jump factor models provide significant improvement in hedging performance in highly volatile market period [2]. The significance of IV structures and in terms of making predictions for market switches is also confirmed [3].

Although HV remains dependable in stable market conditions because of its lower sensitivity to noise. IV generally perform better during times of increased uncertainty. These results figure out that the choice between IV and HV should be based on market regime, and that hybrid models could provide enhanced stability across different market cycles.

3. Theory & methodology

3.1. Hedging theoretical framework

This work is based on the so called Black–Scholes–Merton (BSM) option pricing model. The model offers a closed form expression for European options prices when assuming continuous trading, no arbitrage conditions, frictionless markets and a lognormally distributed asset returns. In this context, delta hedging is the classical risk management strategy which eliminates, as much as possible, variations in the underlying asset’s price through the subsequent variation of its hedge ratio over time.

Beyond delta, the other higher-order sensitivities, like gamma (Γ) and vega (ν), affect the frequency and magnitude of hedging adjustments. Gamma denotes the curvature of the option value as function of the underlying price and vega stands for the sensitivity of the option value with respect to changes in its volatility − a very important quantity when comparing the potential hedging according to various vol estimates.

The use of implied volatility (IV) or historical volatility (HV) can significantly influence the computation of the delta in hedging; this of course influences the quality of hedging [2]. The introduction of market observed volatility measures could lead to pricing biases and can become particularly important in the presence of jumps or regime switching behavior [2].

3.2. Volatility estimation methods

In this study, volatility is estimated using two approaches: Historical Volatility (HV) and Implied Volatility (IV). HV is calculated from the realized fluctuations of past returns, with a 30day rolling window of daily returns adopted in line with common optionpricing conventions. This measure provides a stable, backwardlooking indicator of market variability, but it tends to adjust slowly to sudden changes in market conditions. IV, by contrast, is obtained by inverting the BlackScholesMerton (BSM) model to solve for the volatility parameter that minimizes the squared difference between observed SPY option prices and their theoretical BSM values. Unlike HV, IV reflects the market’s forwardlooking expectations regarding risk sentiment and can capture phenomena such as the implied volatility smirk [3].

3.3. Hedging performance metrics

We adopt three well-established metrics to assess hedging effectiveness in the present study. To penalize for larger deviations between the hedged portfolio’s return and target and reflect extreme hedging errors, we use Root Mean Squared Error (RMSE), which is ubiquitous in model performance assessment [5]. Second, We utilize Mean Absolute Error (MAE) to quantify hedging error on average as the weighted sum does not capture the impact of outliers thus would overscale performance of average cases; its superiority over RMSE in representing average error has been demonstrated extensively [6]. Last, PnL Volatility represents the level of uncertainty for returns on hedged portfolio and a proxy for its residual risk post hedging. Return volatility is not only a key attribute when considering the risk of a portfolio in empirical finance, for which an precise estimation of the volatility is crucial to achieve proper portfolio control and optimization [7]. But it can be used in combination with this framework’s characteristics: in this context, the higher the valuation number is and the smaller its volatility, the better a given security’s hedging capabilities are in that particular model.

3.4. Empirical implementation

In the empirical analysis, the SPDR S&P 500 ETF Trust (SPY) is selected as the underlying asset, with a European call option of strike price USD 628 and a maturity of 30 calendar days serving as the instrument under study. The sample period spans five consecutive trading days. The required market inputs include the daily closing prices of SPY, a 30day rolling history of option prices for implied volatility estimation, the threemonth U.S. Treasury bill rate, and the option’s time to maturity in calendar days. The calibration set for implied volatility estimation comprises ten SPY option contracts, consisting of five calls and five puts. Regarding the hedging procedure, on Day 0 the hedging portfolio is established using the delta calculated from either implied volatility or historical volatility. From Day 1 to Day 4, implied volatility is recalibrated daily using updated market prices, historical volatility is updated based on a 30day rolling window, deltas are recomputed, hedge positions are adjusted accordingly, and the cash account is updated with accrued interest. On Day 5, the portfolio is liquidated, and the hedging error is computed as the deviation between the option’s actual payoff and the final portfolio value.

4. Case study & empirical analysis

4.1. Research objective

The aim of this paper is to empirically assess the hedging performance of IV based and HV-based delta hedging strategies on SPY European options under the BSM model, on a short-term horizon.

4.2. Data and sample characteristics

For this analysis, we use the SPDR S&P 500 ETF Trust (SPY) as the underlying asset. The dates of the study correspond to the period of 14 January 2025 to 18 July 2025, and the hedging horizon is five trading days. The hedging target is an at the money onehanded European call option with a strike of USD 628 and a term of 30 calendar days to maturity. Market data consist of: SPY daily closing prices, three month U.S. treasury discount rate, treasury bill rate, and an history of option prices (30 day rolling). For implied volatility estimation, the calibration set is formed by ten SPY option contracts (five calls and five puts).

4.3. Methodology recap

Implied volatility is estimated by minimizing the squared error between observed market prices and Black–Scholes model prices, using the calibration set described above. Historical volatility is computed from 30day rolling log returns, annualized. Daily deltas are obtained by substituting either the calibrated implied volatility or the historical volatility into the Black–Scholes–Merton framework. The hedging protocol begins on Day 0 with the establishment of the delta-hedged portfolio. From Day 1 to Day 4, implied volatility is recalibrated daily using updated market prices, historical volatility is updated using the rolling 30-day window, deltas are recomputed, hedge positions are adjusted accordingly, and the cash account is updated with accrued interest. On Day 5, the portfolio is liquidated, and hedging performance is evaluated using root-mean-square error (RMSE), mean absolute error (MAE), and the volatility of the profit-and-loss (PnL) series.

4.4. Results analysis

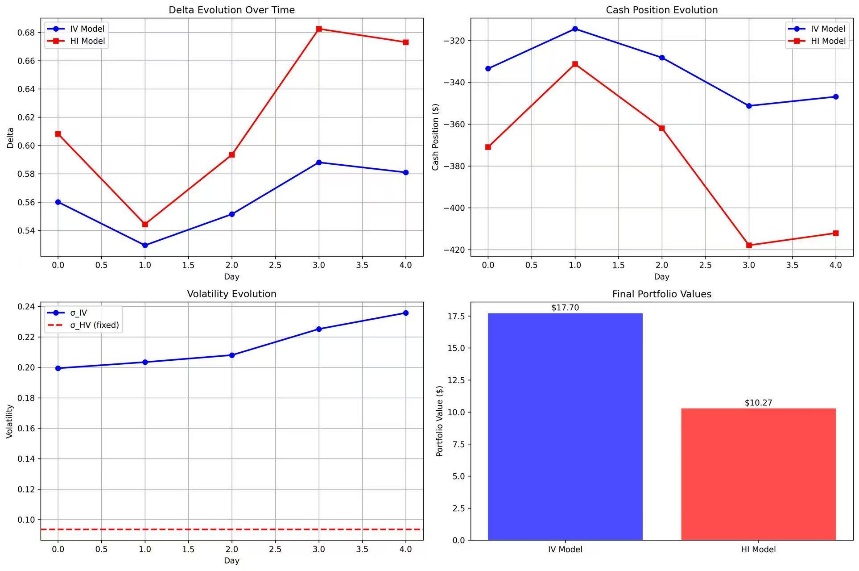
Over the evaluation, the IV model’s delta exhibited a gradual increase from 0.5601 to 0.5810, reflecting a smooth and consistent adjustment to rising volatility expectations. In contrast, the HV model responded more abruptly, with a pronounced jump to 0.6825 on Day 3, suggesting a slower initial reaction followed by an exaggerated correction. In terms of cash position dynamics, both models achieved their peak cash holdings on Day 1. However, the HV model subsequently experienced a substantially larger drawdown, indicating higher rebalancing costs and less effective cash management. The volatility estimates further highlight the divergence between the two approaches: the IV model’s implied volatility rose from 0.1994 to 0.2358, capturing the market’s recognition of increasing shortterm risk, whereas the HV model maintained a constant value of 0.0936, failing to reflect shortterm volatility fluctuations. These differences translated into markedly distinct performance outcomes. The IV model achieved a final portfolio value of USD 17.70, significantly higher than the HV model’s USD 10.27. However, the IV model also recorded a larger hedging error of USD 13.12 compared to USD 5.69 for the HV model, indicating that while the IV approach was more responsive to market conditions and generated higher returns, it also entailed greater residual risk.

Interpretation: Although the IV model tracked market volatility more responsively, its higher sensitivity led to greater hedging error in this short sample, as Figure 1 shown. The HV model, despite being static, produced a lower error—likely due to the relatively stable underlying price path and the absence of large shocks during the period.

5. Discussion

We experimentally show that the degree to which IV and HV hedging are effective as hedge depends on the context of the market. For calmer periods, our result shows that using HV-based delta hedge is still effective, with lower tracking error and transaction cost, which implies that backward looking of HV is somewhat beneficial when the speed at which volatility dynamics change is slow. On the other hand, in times of high volatility and due to structural breaks the IV-based rules perform better as options capture forward looking information. The asymmetric role of regimes highlights the relevance of regime adaptive hedging systems for SPY/S&P 500 options.

Empirical literature strongly documents the relative performances of volatility indicators and option pricing models, and so deserves a proper basis for our interpretation. A comparison between various option pricing models, such as those with stochastic volatility, stochastic interest rates and jumps was presented [8]. With S&P 500 index options, models were evaluated from both the point of internal coherence and out of sample pricing and hedging performance, and it is concluded that stochastic volatility is the single most important feature for providing enhanced hedge accuracy and improved pricing realism [8]. The predictive relationship between implied and realized volatilities was studied, and a non-overlapping data sampling technique that alleviates serial correlation bias in prior analyses was employed [9]. The results suggest that implied volatility essentially incorporates all the information in historical volatility for forecasting future realized volatility, reinforcing the status of implied volatility as forward-looking risk measure [9]. In complement of those views, Andersen et al. further volatility modelling by explicitly modelling jump components in return processes [10]. Their findings indicate that a satisfactory measure and reliable forecast of the volatility can only be obtained by taking into account the presence of the jumps [10]. This is particularly of interest for the considered high frequency financial data, since these results are closely linked to the daily risk management and hedging strategy formulation. Collectively, these investigations support a solid conceptual and empirical ground for our direct comparison between historical and implied volatility. Their findings substantiate the systematic benefit of HV in non-moving markets and the informative role of IV in moving markets.

Although our results go in line with most of the literature in the topic, they give indications which deserve a deeper analysis. For instance, we observe a tendency for the relative performance disadvantage of IV- and HV-based approaches to become larger in presence of volatility clustering, indicating that hybrid models which combine the robustness of HV and the foresight of IV might lead to even better hedging results. In addition, transaction costs (especially for high frequency rebalancing) can significantly change the relative net advantage of one strategy versus another.

A limitation of our study is the exclusive focus on SPY options, which may not generalize to less liquid markets or assets with different volatility structures. Future research could extend this framework to international equity indices, commodities, or fixed-income derivatives, and explore the integration of alternative volatility estimators such as realized volatility from intraday data or model-free implied volatility measures. Moreover, incorporating macroeconomic state variables into the hedging decision process could further enhance regime detection and strategy selection.

6. Conclusion

This paper compared the performance of the HV- and the IV-based delta hedging for SPY call options. Given that the conditions of the sample period were relatively calm, the HV strategy could generate a considerably smaller cumulative hedging error compared with that of the IV strategy. Our results were consistent with a notion that the performance of the measures of volatility varies across market conditions, namely, the HV will potentially be the optimal one under relatively calm conditions, whereas the IV may be used under relatively volatile and/or even-driven circumstances.

The contribution of this paper is that it supplies empirically the conditional performance of HV and IV in hedging. Future work can further enrich this investigation with higher frequencies and longer horizons, different market regimes, and hybrid volatility models in order to enhance robustness.