1. Introduction

For many centuries, architecture has followed Euclidean geometry, their shapes are simple geometry shapes (triangle, rectangle, et al.), and it also gives people a way to realize engineering calculus.

Besides, some engineers got inspiration from nature, resulting in a majority of natural lives being fractal, many architectures are based on fractal geometry, which is a new field created in 1975 by Mandelbrot. It is subject to research irregular geometry, its theory is under certain conditions, each part of an object shows similarities with the whole object (form, structure, information…), called self-similarity. Fractal is composed of four aspects, box dimension, self-similarity, fractal method, and fractal application.

Many architectures were built with the shape of the fractal, this paper looked them up, analyzed why they are fractal buildings, and computed their box dimension, to see how important is to use fractals in architectures.

2. Basic background of Fractal geometry

2.1. Who created fractal geometry?

Fractal geometry was developed by the French-American mathematician Mandelbrot, who is usually known as the father of fractals. The first edition of his book ‘Les Objects Fractals: Forme, Hasard et Dimension’ (1975) laid the foundation for the study and the exploration of fractals in a variety of disciplines. In 1982, Mandelbrot published a highly influential and readable book, ‘The Fractal Geometry of Nature’. This led to the widespread recognition and popularization of fractal geometry in the field of mathematics. The term “fractal” was coined by Mandelbrot, and used to describe objects that were irregular or fragmented to fit into a traditional geometric setting [1]. He derived the term ‘fractal’ from the Latin word ‘fractus’, which means fractured, or fragmented. He used this term to describe every complex and irregular geometric object in nature that cannot be analyzed by traditional Euclidean geometry. According to Mandelbrot— “A fractal is a mathematical set to concrete object that is irregular or fragmented at all scales.”

2.2. Basic Theory

Fractal geometry is a workable geometric middle ground between the excessive geometric order of Euclid and the geometric chaos of general mathematics [2]. The term “geometry” in the context of fractals has a broader meaning than in traditional geometry. While traditional geometry deals with well-defined shapes and Euclidean concepts, typically visualizing the object of study as a regular pattern, fractal geometry explores irregular and self-similar patterns that can be incredibly complex and self-similar at different scales. This means that general mathematics lacks the specific structure found in geometry, making it challenging to apply to tangible phenomena. Fractal geometry challenges the traditional notions of smoothness and regularity in geometry and provides a new way of modeling and analyzing the intricate and irregular patterns found in the natural world.

According to Kenneth Falconer (1985), a fractal exhibits the following properties [3]:

Ability to be differentiated and to have a fractal dimension;

Self-similarity;

Multi fractal scaling;

IV) Fine and detailed structure at any scale;

V) Simple and recursive definitions.

Fractals are infinitely complex patterns that are self-similar without ever repeating. They exhibit self-similar across different scales due to iterations. If it has undergone a transformation whereby the dimensions of the structure were all modified by the same scaling factor. The resulting shape remains self-similar. This means that while the size, orientation, and position of the fractal may change, its overall shape remains consistent with the original fractal structure. It is also important to note that not all fractals are strictly self-similar. Some fractals exhibit variations in self-similarity due to their inherent complexities and randomness.

The presence of these properties can be readily observed in nature since nature is full of fractals. Here are a few notable examples:

I) Ferns and plants;

II) A puffy cumulus cloud;

III) Coastline;

Snowflakes.

They have the same common features that they are continuous yet non-differential, meaning they lack smoothness and exhibit intricate detail at all levels of magnification. For example, coastline often exhibit self-similarity at different scales, appearing curved and irregular but not smooth when examined in detail.

Unlike geometric objects with integer dimensions, fractals often have fractional or non-integer dimensions. This dimension, known as the fractal dimension of Hausdorff dimension, quantifies the space-filling capacity of a fractal. This is because these curves have infinite details, so if you measure it with a 1-dimensional straight line, the value is infinity, yet they do not fill a finite plane so their dimension cannot be equal to 2. Therefore, many fractals have dimensions between 1 and 2.

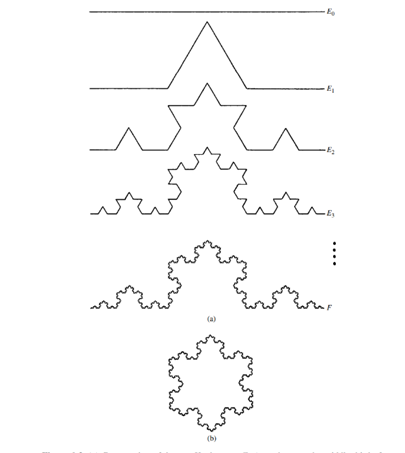
Figure 1. Koch’s snowflake [4].

Here are some typical strictly self-similar fractals:

\( Mass scaling factor: \frac{1}{4};Dimension equal to 1.2619= log3(4)\ \ \ (1) \)

is fractal is called Koch’s snowflake because it was first conceived by the Swedish mathematician Helge von Koch in 1904. It is a classic example of a curve that is continuous but nowhere differentiable. It displays exact self-similarity in that each part or section is identical to the whole curve. It is made of four “quarters” each similar to the whole but scaled by a factor \( 1/3 \) . It is constructed by iteratively adding smaller triangles to the sides of an equilateral triangle, and this process can be repeated infinitely.

The algorithm for constructing the Koch’s snowflake [3]:

1) Start with an equilateral triangle, and divide each side of the triangle into three equal segments.

2) For each of the middle segments, remove the middle third of each side.

3) Draw another equilateral triangle, with its sides being equal to one-third of the sides of the initial triangle, one of its sides replacing the line segment removed, and the other two sides lying outside the initial triangle.

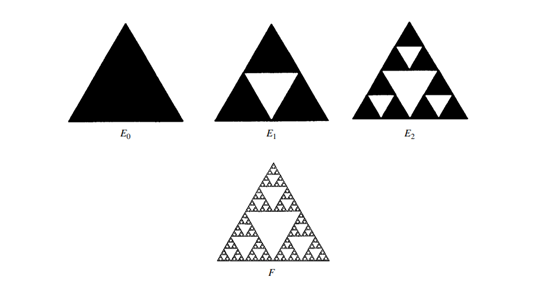
Figure 2. Sierpinski triangle [4].

\( Mass scaling factor: \frac{1}{3}; Dimension equal to log2(3)= 1.585\ \ \ (2) \)

e Sierpinski triangle is a famous fractal pattern that is constructed iteratively. It shows self-similarity at different scales. It is made of three smaller copies of itself, and the side length of each smaller triangle is half the side length of the original triangle.

The algorithm for constructing the Sierpinski triangle:

1) Start with an equilateral triangle, divide it into four smaller equilateral triangles by connecting the midpoints of its sides.

2) Remove the central triangle.

3) Repeat the process for each remaining smaller triangle.

2.3. Fractal and its application

Fractals and their recursive properties have made them highly desirable in computer-generated graphics and various applications. In particular, iterated function systems have high compression ratios, up to 1:1000, and have broad applications in graphics and communications. For example, in the movie “Star Trek II: The Wrath of khan,” the planets and other spectacular scenes are generated by Piksha company on a computer. The mountains that are created by computers have also been used by IBM in advertising campaigns. Fractals have also been used to model the spatial and temporal dynamics of ecosystems. This can help scientists better understand the distribution and interaction of species. There are some scientists who believe that fractal geometry can help them understand the structure of living cells and the structure of diseased cells.

3. Architecture example 1 based on fractal geometry

3.1. Architect and innovation of TOD’s

A famous building is called TOD located in Tokyo Japan, designed by Toyo Ito in 2004, the architect is known as “one of the world’s most innovative and influential architects”, his innovation is to combine the physical and virtual world to solve the current problem of ‘simulated city’ in Japan [5]. TOD is the most bustling shopping center in Tokyo, the total surface area of the building is 27448 square feet, with a 33-foot length of the street next to the building. The inner construction has 7 levels, including 3 levels of shoe shops, 6 levels of activity spaces, the top 2 levels of offices, private meeting rooms, and a roof garden. What is more, the outer shape looks like a massive L, wrapped around concrete and glass walls with the pattern of a tree, As Figure 1 shows, the glass needs to support the whole building due to there is no pillar in the building. Toyo Ito used a completely different way from traditional geometry to contribute a new structure, which is fractal geometry. He was inspired by fractal objects in nature and combined them with this building [6].

3.2. Group self-similarities during the growth of natural form

It broke symmetric mimicry in traditional buildings and mimicked the form, which is the growth of natural lives, it is a way to achieve the group self-similarities. It is undeniable that this mimic is not the simple representation of static shape of organism, it is more like to emphasise the different intermediate states during the growth process.

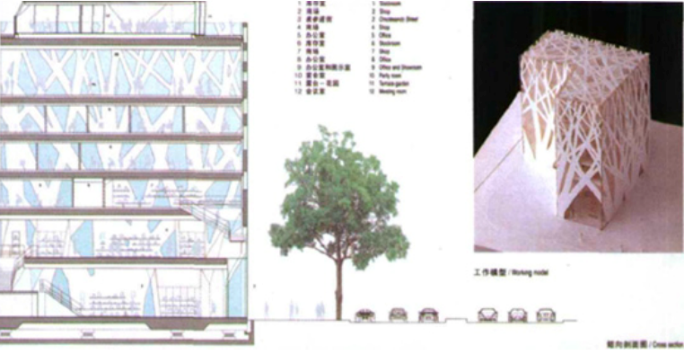
Figure 3. Cross-section is drawn of the outer pattern of the building [5].

3.3. Fractal attraction of unregular natural lives

Ito’s inspiration was from nature, especially from branches and trees. The fractal pattern of trees looks really complicated but using the computer to simulate the process of the growth is simple. The pattern basically copies and overlaps the shapes of the abstracted trees in order, showing the same patterns in each small part of the overall pattern, which is self-similarity, shown in Figure 2, representing the fractal pattern of plant nutrient transport system [7].

Figure 4. Details of outer walls [7].

3.4. Representation of self-similarity in different degrees of space linking to the construction of TOD’s

Repeated the same or similar operations in different scale-spaces, to achieve a nest in space, regardless of whether the operation is aimed at the real object, the boundaries, and the space itself, are all effective processes of making space self-similarities. In this case, the simple operations in these different layers of repeating could express strong feelings.

The bottom of TOD is shops, the top is office and activity places, it relates to the structure of trees. The bottom is a public commercial space, like the bottom of the tree, sparsely branched, the top is a more private space, which is like the tree crown, with dense leaves. In general, it shows layers by layers nest, by coping and overlapping images of trees, showing the fractal self-similarity of geometry on TODs [7].

4. Architecture example 2 based on fractal geometry

4.1. Architect and of rockery in the Master-of-Nets Garden in Suzhou’s classical gardens

Suzhou’s classical Gardens was listed as a Chinese heritage site under state protection in 1988, and it was also listed as a World Heritage site by the United Nations Educational Scientific and Cultural Organisation (UNESCO) Heritage Committee in 1997. The rockery was built by Yuliang Ge (1764-1830), who was a famous artist and landscape gardener in the Qing dynasty, in ancient China. During that time, the shape and contour of the rock is an important standard for the selection of rockery stones in classical gardens, and it is also an essential standard for measuring the form of rockery. The technique of making rockery is similar to the linear transformation of fractal composition method, the rockery and its elements also conform to the ‘irregular shape’ principle of fractal geometry theory [8].

4.2. The statistics of data and analysis box dimension

Rockery often has multiple viewing surfaces with different positions. According to this, the main factor is to determine the contour line of rockery, which is mainly based on a group of stones, plants, and buildings with sky and walls as background, like Figure 3 shown below, computing their box dimension, by using this formula:

\( D=\underset{ε→0}{lim}{\frac{log{c-log{N(ε)}}}{log{(ε)}} }\ \ \ (3) \)

Figure 5. Patterns shown here from left to right are the origin picture of rockery, rockery, rockery and building, rockery and plants, building, building and plants, and the combination of rockery, building and plants, and plants [9].

By computing box dimension, this research found the picture of rockery in Suzhou’s classical gardens, and overlapped it by different sized squares, counting the number of squares occupied the outline of rockery, and sub the values into the formula to get box dimension, then plot a graph by \( log( N(ε)) \) in y-axis with \( log (\frac{1}{c}) \) , it shown a straight line, data is shown below.

Figure 6. Origin picture of one viewing surface of rockery [9].

Table 1. Box dimension of each element of rockery in figure 5

Figure 7. The origin picture of the other viewing surface of rockery [9].

4.3. Summary

These data show that the box dimension of irregular shapes is higher, for example, the box dimension of a single building and rockery is lower than that of a combination of rockery, plants, and buildings. However, it does not mean higher box dimension is better, some research shows higher box dimension also gives visitors a sense of monotonous. In this case, by building buildings and rockery, it is better to find an optimum value.

5. Architecture example 3 based on fractal geometry

5.1. Parametric Architectural Strategies in L-System

Due to its ability to generate naturally aesthetic features through fractal geometry, it reflects the generation and iteration of nature in various ways, making more architects willing to use fractal geometry for architectural construction. Thus, the L-system was born [10]. L-System, as described by a biologist called Aristid Linder Mayer, in 1968, a string rewriting system was proposed for the generation of constituent patterns, which used string iteration to generate branching fractal patterns simulating plant growth [11]. Parametric architectural design, on the other hand, revolves around establishing a parameter model by defining the interconnections between external and internal factors in the architecture. The convergence of L-System and parametric architectural design lies in their shared emphasis on model creation. This shared aspect finds its realization through computer software, where relevant parameters are configured to dictate initial values, iteration rules, and the number of iterations.

L-System possesses the capability to generate both two-dimensional tree-like images and three-dimensional tree structures. The visual representation of these tree-like structures is remarkably intuitive, evoking a sense of natural human perception. Furthermore, they have the potential to imbue architectural spaces and facades with distinctive characteristics and spatial sensations across various scales and levels.

Figure 8. Tree branch structure generates the schematic [11].

5.2. Fractal Parametric Architectural Design Applications of L-System

The Stuttgart Airport Terminal, designed by German architect Frei Otto, originally featured a regular square-shaped waiting hall. However, Otto employed a three-dimensional tree-like design concept, utilizing steel columns to simulate the growth and form of trees, resulting in a space imbued with a natural, dynamic, and nonlinear spatial sensation. Guiding the generation of architectural structures and the creation of spatial atmospheres in this instance was none other than the L-System [12].

Figure 9. Interior of the Stuttgart Airport Terminal.

Figure 10. Appearance of the Stuttgart Airport Terminal.

5.3. Summary

The L-System fractal algorithm serves as a unifying nexus, achieved through the creation of parameter models, which can then be visually articulated to convey the concept of fractals. Subsequently, it facilitates the design of geometric forms, enabling the implementation of parametric fractals in architectural design strategies. Moreover, it underscores how the theory of fractals inherently embodies characteristics rooted in nature and human perception.

Figure 11. Figure in Parametric Architectural Design based on Fractal Iteration, by Yalong Mao [12].

6. Conclusion

Fractal geometry is trendy because it has many uses, such as in graphics and communications, modelling, the spatial and temporal dynamics of ecosystems, and helping people to research cells in biology, and the background is deep enough to be worth exploring. Fractal geometry has also been used in the construction of buildings and rockeries, and it has helped many architects find the best value for these buildings and rockeries, such as the Suzhou Garden. Fractal geometry has also been applied to the construction of many buildings and rockeries, and it has helped many architects find the best value for these buildings and rockeries, such as the Suzhou Garden. Lin’s system expresses the concept of fractal geometry by building a parametric model. From this, Lin’s system developed more and more and finally succeeded in combining it with nature, resulting in a building similar to the Stuttgart Airport Terminal. Inside, the roof is well supported by tree branches of fractals and iterations, leaving more space for people to move around and being more aesthetically pleasing. People can use Fractal geometry more often daily.

Author Contribution

All the authors contributed equally and their names were listed in alphabetical order.