1. Introduction

In 1853, American Eliza Graves Otis showed the world his invention, the elevator, at the World's Fair held at the Crystal Palace in New York. This lifting device invented by Mr. Otis changed the way people get around, replacing to some extent the traditional means of elevation, the staircase, and has become an important means of transportation for most of today's high-rise buildings [1].

At first, most of the buildings are used in a single elevator, but with the continuous development of society, a single elevator gradually unable to meet the needs of the people, so the emergence of a group of elevators composed of multiple elevator linkage control system.

Then, how to effectively use multiple elevators has become a consequent problem. As the population rises, the number of jobs and the number of people required increases, the problem of long waiting time and long travel time during the peak period of elevator use becomes more and more significant, especially during the morning and evening rush hours on weekdays.

Given that most office buildings are unable to expand the number of elevators, optimizing elevator scheduling is the most logical solution.

2. Case Study

An office building in Beijing has 22 floors above ground and 3 underground buildings, a total of six elevators. The maximum carrying capacity of each elevator is 20 normal adult mass. Assume that the underground building portion is not considered. The average dwell time of each elevator on the first floor is 20s, the average running time between floors is 3s, and the average dwell time on floors 2-22 is 10s, and all the elevator passengers can enter and exit the elevator within the average dwell time. Our goal is to rationalize the design of the elevator operation scheme so that all office workers can reach the office floors in the shortest time during the morning peak period. The number of office workers corresponding to each floor is shown in the table below.

Table 1. Amount of workers in each floor.

3. Model assumptions and notation

3.1. Model Assumptions

(1) Employees working in this office building take the elevator, not the stairs

(2) During the morning rush hour, there are only people going up the elevator and no people going down the elevator

(3) Every floor within the elevator's transportation range (except for the 1st floor during the morning rush hour) has passengers exiting the elevator

(4) There are no accidents in the elevator during operation

3.2. Notation

\( n \) : the maximum number of floors to be transported by the elevator in a single cycle;

\( {t_{1}} \) : average running time of the elevator between each floor;

\( {t_{2}} \) : average dwell time of the elevator per stop;

\( {t_{3}} \) : average dwell time of the elevator on a floor;

\( {T_{avg}} \) : average passenger arrival time;

\( i \) : number of sequences in the service area;

\( {T_{i}} \) : arrival time per cycle for elevator i in the service area;

\( {T_{i}}(n) \) : arrival time per cycle of service area i elevator at \( {s_{i}}=n \) ;

\( {P_{i}} \) : total number of people in service area \( i \) ;

\( {s_{i}} \) : the highest floor that service area i elevator is responsible for transporting;

\( {T_{A}}(i) \) : arrival time of the \( i \) th passenger;

\( {W_{p}} \) : the total number of passengers on the elevator;

\( {W_{p}}(i) \) : the total number of elevator rides in service area \( i \) ;

\( {T_{w}}(i) \) : waiting time of the \( i \) th passenger for the elevator;

\( {T_{t}}(i) \) : elevator ride time of the \( i \) th passenger.

4. Introduction to elevator group likage control system

4.1. System structure

Elevator group linkage control system is a fairly complex system, involving hundreds of signals sent and received, processing. Elevator group control has a variety of ways to achieve, but their control system principle is the same, the structure is similar. The following figure shows a basic structure of the elevator group control system block diagram [2].

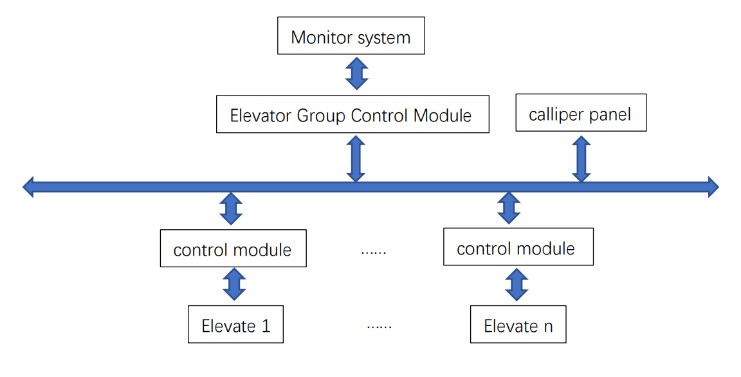
Figure 1. Elevator group control system

4.2. System features

(1) Uncertainty

The elevator group linkage control system has a very large number of uncertainties, such as the internal environment of the elevator and external environmental factors, the target floor of the occupants and the call location, etc. These uncertainties will have a large impact on the prediction of the average arrival time of the elevator, resulting in model errors.

(2) Multi-targeting

The operation of the elevator group to achieve a number of goals: short average waiting time for passengers, short average passenger ride time, the comfort of the passengers in the elevator should be guaranteed and so on. Such objectives affect the development and measurement of the model evaluation criteria.

(3) Disturbance

Elevator operation will be disturbed by a number of factors, for example: passengers enter the elevator and mistakenly press the floor, resulting in the elevator running time elongated; passengers due to their own physical reasons lead to the slow speed of the elevator, prolonging the waiting time of other passengers; passengers mistakenly touch the elevator alarm button, resulting in the elevator stopping and so on. These disturbing factors will make the model produce errors [3].

(4) Non-linear

The operation of the elevator is not linearly correlated, in different traffic operation modes, the priority of the elevator response will change; once the elevator reaches the full capacity of the number of people, it will not respond to calls from other floors in this cycle. The nonlinear characteristics will bring obstacles to the prediction of the model [4].

(5) Incomplete information

The elevator is unable to intelligently estimate the number of people boarding the elevator and the target floors of the passengers and is not good at predicting the degree of crowding in the elevator. This fuzzy information will likewise bring difficulties to the design of the model.

4.3. Model evaluation metrics based on system characteristics

To sum up, this paper will set the evaluation index of the model as "to make the final average arrivaltime \( {T_{avg}} \) shortest", so this paper will take "to make the final average arrival time \( {T_{avg}} \) shortest" as thegoal of modeling, to solve the optimal operation of the elevator program, where

\( {T_{avg}}=\frac{\sum _{i=1}^{{W_{p}}(i)}{T_{A}}(i)}{{W_{p}}}, \)

\( \sum _{i=1}^{{W_{p}}(i)}{T_{A}}(i)=\sum _{i=1}^{{W_{p}}(i)}{T_{w}}(i)+\sum _{i=1}^{{W_{p}}(i)}{T_{t}}(i) \) .

The precondition for model establishment is assumed that the errors and disturbances caused by the characteristics of elevator group linkage control system do not exist.

5. Analysis of elevator passenger traffic patterns and scheduling

5.1. Upward peak traffic patterns

The upward peak traffic pattern mostly appears in the morning rush hour, with the operation pattern of conveying passengers from the ground floor (because this article does not consider the underground part of the building, so the bottom floor is the first floor) to the floors above the first floor. When the upward peak period comes, the office elevator is faced with the problem of how to quickly transport all passengers to the designated floor. Because it is the morning rush hour, convergence in the lower floors of the staff are to take the elevator to go up, so we can think of the morning rush hour only the upward movement of people, there is no downward movement of people and each floor has people leaving the elevator.

5.2. Comparison of common elevator operation methods

In order to simplify the model without loss of generality, two elevators are assumed to operate independently at the same time in the comparison, transporting all passengers from one floor to the specified floors. There are various criteria for comparing elevator operation schemes, but here the optimal scheme is selected based on the criterion of "total elevator operation time", and T [5]. is calculated based on the ratio of elevator operation period/total operation time equal to the number of passengers transported by the elevator in one cycle/total number of passengers transported. (Assume that the number of people working on each floor is 100 and there are 10 floors. The maximum capacity of the elevator is 20 persons, the average dwell time of each elevator is 20s on the first floor, the average running time between floors is 3s, and the average dwell time on floors 2-9 is 10s.)

(1) Tiered Approach

Each elevator stops at each floor.

\( \frac{40}{900}=\frac{164}{T} \)

Thus, \( T=3690s \)

(2) Single- and Double-Stacking Method

One elevator stops only at the 1st and odd-numbered floors, and the total time used is \( {T_{1}} \) ; the other elevator stops only at the 1st and even-numbered floors, and the total time used is \( {T_{2}} \) .

\( {T_{total}}={T_{max}}({T_{1}},{T_{2}}) \)

\( \frac{20}{400}=\frac{108}{{T_{1}}}, \frac{20}{500}=\frac{124}{{T_{2}}} \)

\( Thus, {T_{1}}=2160s, {T_{2}}=3100s \)

\( {T_{total}}={T_{max}}({T_{1}},{T_{2}})=3100s \)

(3) Segmentation Scheme

With six floors as the dividing line, the first elevator is responsible for transporting floors 2-6 and the total time used is \( {T_{1}} \) ; the second elevator is responsible for transporting floors 7-10 and the total time used is \( {T_{2}} \) .

\( \frac{20}{500}=\frac{100}{{T_{1}}}, \frac{20}{400}=\frac{114}{{T_{2}}} \)

\( Thus, {T_{1}}=2500s, {T_{2}}=2280s \)

\( {T_{total}}={T_{max}}({T_{1}},{T_{2}})=2500s \)

(4) Combination of Layering and Segmentation

Using the fifth floor as the dividing line, the first elevator is responsible for transporting floors 5-10, and the total time used is \( {T_{1}} \) ; the second elevator makes stops at each floor, and the total time used is \( {T_{2}} \) . On average, each passenger has a 50% chance of choosing each elevator.

\( \frac{20}{300}=\frac{134}{{T_{1}}}, \frac{20}{600}=\frac{164}{{T_{2}}} \)

\( Thus, {T_{1}}=2010s, {T_{2}}=4920s \)

\( {T_{total}}={T_{max}}({T_{1}},{T_{2}})=4920s \)

In summary, the segmented operation method is more reasonable and efficient.

5.3. Dynamic programming to solve partition points

5.3.1. Artificial Preliminary Subdivision. If the elevator group linkage control system is used to implement segmented operation for 6 elevators, it is necessary to specify the partition point. In this paper, the 6 elevators in the office building are divided into 3 service areas, and each service area has 2 elevators running within the specified range. According to the distribution of the number of office workers in the office building, the preliminary partition is shown in the following table:

Table 2. Preliminary partition

Total time to complete transportation of all passengers.

For service area \( i \) , the sum of arrival times of all passengers:

\( {W_{i}}= [\frac{{P_{i}}}{20}]×{T_{i}}-3({s_{i}}-1) \)

Where \( {P_{i}} \) ( \( i=1,2,3 \) )denotes the total number of passengers that the service area is responsible for transporting, and [ ] is rounded upwards, since the time of descending from the highest to the lowest level after the last transportation is completed does not need to be taken into account, and is therefore subtracted by \( 3({s_{i}}-1) \) .

5.3.2. Dynamic Programming Modelling for Optimal Solutions Based on Preliminary Partitioning. In this paper, the per capita arrival time of the three service areas cannot differ by more than 5s as a constraint, and the dynamic planning model is established to further optimize the partitioning scheme on the basis of the preliminary partitioning.

\( {T_{i}}({n_{1}})=400+10×\frac{(40-({n_{1}}-2)∙[\frac{20}{{n_{1}}-1}])∙({n_{1}}-1)}{2}+3×2({n_{1}}-1) \)

\( {T_{i}}({n_{2}})=400+10×\frac{(40-({n_{2}}-{n_{1}}-1)∙[\frac{20}{{n_{2}}-{n_{1}}}]∙({n_{2}}-{n_{1}}))}{2}+3×2({n_{2}}-1) \)

\( {T_{i}}({n_{3}})=400+10×\frac{(40-({22-n_{2}}-1)∙[\frac{20}{22-{n_{2}}}])∙(22-{n_{2}})}{2}+3×2(22-1) \)

\( {T_{avg}}(n)=\frac{{T_{i}}(n)∙[\frac{{W_{p}}(i)}{20}]}{{W_{p}}(i)} \)

Since the difference in per capita arrival time between the three service areas was no more than 7s, it was derived by programming (see appendix for code):

𝑛1 ∈ {8,9,10}

𝑛2 ∈ {15,16,17}

𝑛3 ∈ {22}

In this regard, the problem is transformed into a problem of solving the shortest path:

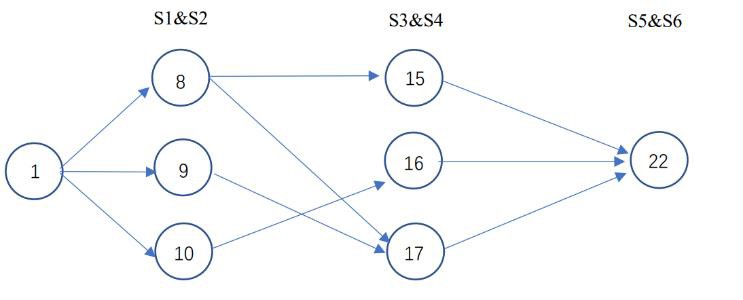
Figure 2. Shortest path

So, there are the following four plans:

Table 3. Plans

In summary, the optimal solution for the elevator operation model in the morning peak period is:

Table 4. Optimal solution

6. Conclusion

6.1. Advantages of the model

The purpose of the research is clear; first, the research significance and background of this topic is explained, then the common elevator operation system - elevator group linkage control system is analysed, and according to its characteristics, the evaluation indexes of this paper's model are formulated, i.e., the objective function is determined. Next, this paper mathematically analyses the common elevator operation mode, and determines that the segment operation method is the most effective operation mode. On this basis, this paper first gives a feasible solution, and then based on the preliminary partition using dynamic programming (combined with the C language) to solve the reasonable partition point, and then use the shortest path principle to derive the optimal solution, for the office building planning elevator scheduling has a suggestive work.

6.2. Shortcoming of the model

The assumptions about the behavioural patterns of the elevator occupants are not realistic enough, such as all people take the elevator instead of the stairs, no down-travellers during the morning rush hour, etc. The preconditions are ideal, circumventing the errors caused by the characteristics of the elevator group linkage control system, which will have a certain impact on the model results, and do not take into account the underground building portion.

6.3. Prospects

Consider more objective factors in the model; collect the number of people taking the stairs and their target floors in the morning rush hour every day, fit the data to the actual number of people taking the stairs every day, and simulate the flow of people with MATLAB simulation algorithms; take the underground building into account to enhance the practicality of the model.