1. Introduction

In retrospect, the discovery of quantum Hall effect (QHE) can be dated back in 1980, which wined the 1985 Nobel Prize [1, 2]. Klaus, one of the pioneer and winner of the prize, found the integer Hall effect which can extended the original Hall effect to a broader field. In general, the ordinary Hall effect simply described the motion of charged particles in a particular magnetic field. The Hall effect illustrates how charged particles experience circulation motion when subjected to a magnetic field. For the classical Hall effect, there was an anomalous Hall effect which is found only a years later from Hall effect. Edwin Hall, the founder of Hall effect, observed that the Hall voltage in ferromagnetic materials was 10 times higher than that in nonmagnetic conductors; this phenomenon was later named as the “anomalous Hall effect” (AHE). In 2013, the proof-of-principle experiments for quantum AHE (AQHE) was achieved by Xue et al from Tsinghua University [3]. Later the founding of fractional quantum Hall effect (FQHE) won another Nobel prize in 1998 Tsui, Stormer, Laughlin for their works on interpreting and discovering fractional quantum Hall effect. Additionally, another piece of work regarding QHE earned the third Nobel Physics prize in 2016 -Thouless, Haldane, Kosterlitz successfully applied topology to make revolutionary contributions to their field of condensed-matter physics [4]. Due to its importance, QHE has a large variety of contribution in multiple fields in physics including photonics and quantum entanglement and is considered as one of the most valuable topics. There are several remarkable applications in solid-state physics like the aforementioned topological phase of matter. However, besides the category of solid-state physics, QHE-involved research is popular and applicable in various inter-discipline fields of physics [1].

QHE, since being discovered in 1980, brings an incredible amount of innovational and technological breakthroughs in different categories- major discoveries and theories are created every year. There were continuous studies on the development and extension of QHE. It also incentivized researchers cross the world to make contribution and research in this topic. However, the huge number of papers might be confusing for readers who are interested to this topic to understand. Hence, this paper aimed to summarize and provide intended researchers a brief view on the former progress and the state-of-art application of QHE. Thus, it provides the audience a general view on QHE and some recent applications regards it. The framework of this paper is to first elaborate on the category of the Hall effects (classic Hall effect, IQHE, and the basic explanation and interpretation of different Hall effects; then provide a broad review on the application of the following Hall effects—, QHE, QAHE; finally expound some of the current limitations and future outlooks of the Hall effects.

2. The category of Hall effect

2.1. Classic Hall effect

Classic Hall effect will appear when an external magnetic field exists for a metal-type material. On account of the force generated by the magnetic field, it would lead to the accumulation of the electrons that induce a voltage that causes the electron to move in a circular motion. To give a mathematical description, the Hall coefficient R can be described as [5]:

\( R=\frac{{V_{y}}{t_{z}}}{I{B_{z}}} \ \ \ (1) \)

Here, the Vy is the transverse voltage, I is the current, tz and Bz correspond to the length of the sample and magnetic field components in the z-direction.

2.2. IQHE

As a matter of fact, the Hall resistance could be exactly quantized in the multiples of h/e2, if one subjected a silicon transistor to a high magnetic field. This is the occasion where the IQHE exist since the multiplier on the Hall resistance is a positive integer. The most notable aspect of the data would be that, for a range of magnetic fields, the Hall resistivity plateaus before sharply moving on to the next plateau, which is the reason why it is granted QHE, i.e., the discontinuous and discreteness of the data [1]. A sketch of the IQHE is shown in Fig. 1.

In order to describe the resistivity, which is now quantized in the scenario of IQHE, this formula was introduced.

\( {ρ_{xy}}=\frac{2πℏ}{{e^{2}}}\frac{1}{ν} ν∈Z \ \ \ (2) \)

Extreme accuracy is used to determine whether v is an integer. The quantum of resistivity refers to 2πℏ/e2 (where (-e) is the charge of a single electron). It currently serves as the benchmark for measuring resistivity [7]. The Fig. 2 demonstrates different features of QHEs, for instance, the circular motion in the QHE compared to the classic Hall effect.

2.3. FQHE

On the plateau of FQHE, the Hall resistivity shares the same form of expression as in IQHE, but now with ν to be a rational number other than integer, here ν ∈ Q. However, not every fraction can be taken. The most notable plateau locates at ν = 1/3, 1/5 and 2/5. However, there are much more different than mentioned above and the most of these rational numbers have odd denominators. Although the graph of FQHE is not presented in Fig.2, only in the aspect of the listed properties, FQHE would look exactly alike to IQHE as they are both the subtopic of the described QHE. However, in contrast to the IQHE which can be explained only using free electrons, in order to correctly interpret FQHE, the interaction between electrons should be considered. The fact of interaction between elections makes the problem more complicated but far richer [7].

2.4. Quantum anomalous Hall effect

With regard to the classic AHE founded by Edwin Hall, just similar to illustrated in the introduction, the Hall voltage was discovered to have a prominently larger value in ferromagnetic materials. The “anomalous” in AHE are observed and confirmed in a ferromagnet [8, 9]. The quantum version of AHE was founded shortly later than IQHE in 2013 and is a type of quantized Hall effect locates in a system without magnetic field. The QAHE is a unique representation of topological structure in multiple-electronic systems. In addition, QAHE might possibly have applications in electronic devices in foreseeable future [3]. Moreover, as shown in Fig. 2, it’s clearly illustrated that both classic AHE and QAHE are magnetized; the phenomena of spin-orbit coupling, and disorder effects of QAHE can also be detected based on the section E.

2.5. Quantum spin Hall effect

In the case of classic spin Hall effect (SHE), the spin direction of electrons can affect the force they experience. To be specific, in an external electric field, the motion of electrons can be altered to different paths, as depicted in Fig. 2 where it’s observable that the directions of blue and red electron are different. The name “Spin” Hall effect is granted the existence of the spin current, though no net charge current exists. The SHE, just similar to anomalous Hall effect, doesn’t necessarily need the time-reversal symmetry breaking which allows it to appear in a semiconductor without external magnetic field. Similar to the way that SHE relates to AHE, the quantum version of SHE, the QSHE is also connected to the QAHE, as presented in the f sub plots of Fig. 2.

3. Applications

3.1. The application for Quantum Hall effect

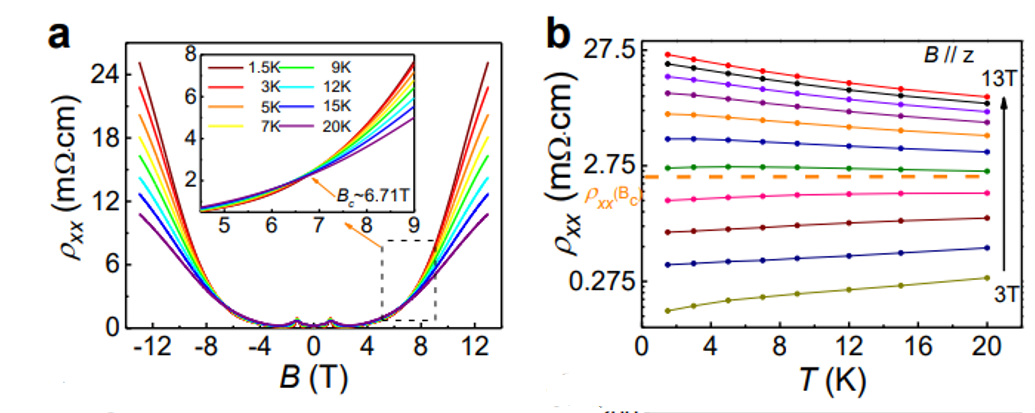
A remarkable application for QHE is the expansion on the dimensions of electronic system. To exemplify, the IQHE originally is a topological phase only in two-dimensional (2D) electronic systems, with disregard on multi-electron interaction [10]. The additional (third) dimension would possibly bring new phenomena such as 1D Majorana chains or 3D fractional quasiparticles. This discovery might be applied to the possibility of creating QHE at room temperature, even without external magnetic field or in other crystals [1]. A typical application results of the resistance is given in the Fig. 3.

3.2. The application for Quantum Anomalous Hall effect

One of the applications include the topic on photonics. To be specific, some of the researchers find a photonic analogue of the QAHE insulator based on 2D array of coupled ring resonators. It is quite different from the previous Haldane scheme, it is translation invariant (i.e., with zero net gauge flux threading the lattice), and exhibits next-nearest neighbor couplings. Furthermore, it should be noted that the rotation direction of photons in the ring resonators constitutes a pseudospin degree of freedom (freedom for the spin precession). As a consequence, it will obtain opposite hopping phases with respective edge states propagating in opposite directions. In this case, these appealing phenomena are promising for the further development of reconfigurable integrated nanophotonic devices for applications in the state-of-art quantum techniques (e.g., computing and teleportation). Photonics has emerged as a versatile platform [11]. A typical results of such an application is demonstrated in Fig. 4.

4. Limitations & Future outlook

Though the discovery of QHE has certainly boosted plenty of innovations, most of its state-of-art applications are not that appealing. The two exampled application clearly elaborate this idea that current applications are quite theoretical and ideal. These discoveries and intended applications create a valuable blueprint while they are not that practical to be applied and affected the majority of population yet. There are barely practical uses for QHE, possibly due to the abstractness and complexity of this topic. However, the lack of current usage can’t necessarily disqualify the exquisiteness and logic under QHE. Just like most of other theoretical physics discoveries, the QHE, may not make this world much better in a glance- unlike the engineering scenario. Nonetheless, QHE can satisfy the unlimited aspiration of mankind toward the ultimate truth of this universe. In fact, it’s one of the most extensively researched topics in physics, which also connects to multiple different topics such as photonic which are all popular genre in physics. In the aspect of future outlook, it is completely plausible to expect some astonishing applications based on the concept of QHE in different categories (e.g., solid state), where QHE is mostly connected or black hole which might sound completely irrelevant.

5. Conclusions

In summary, this paper discusses the principle and state-of-art application of QHE from the perspective of history (categories), definitions and different applications. Specifically, the different types of QHE, these types of history and function are introduced. According to the analysis, the expansion on dimensions of electronic system is one notable recent application. In addition, in the category of photonic, QHE can contribute to the finding of both classic and quantum’s information processing. Nevertheless, there are not that much practical uses of QHE, despite the fact that QHE has a number of intended applications that may lead to a technological boost. In the future, there might be some outstanding works and influential application regarding the topic of QHE. Overall, these results offer a guideline for researchers that are interested in QHE and shed light on the possible applications in QHE.