1 Introduction

Elementary number theory is a very old branch of mathematics that studies the properties of integers in a completely original way. Due to the fast progress in computing science and electronic technology, number theory has evolved from being solely a branch of pure mathematics to a field with several practical applications, particularly in cryptography [1].

Domestic researchers have extensively applied their knowledge of number theory in many research endeavors, resulting in a substantial accumulation of valuable research findings. The application of number theory in cryptography is demonstrated by the use of classical ciphers, RSA ciphers, and probabilistic encryption in literature. Foreign scholars, including W. Stein, N. Koblitz, B. Hutz, and others, have conducted extensive research on the application of elementary number theory in cryptography, similar to domestic research. They have provided numerous results from their studies.

This work primarily discusses the practical implementation of elementary number theory concepts in character cipher, RSA public key cipher, and other encryption systems, as well as secret key sharing. Prime number theory, Euler's theorem, congruence theorem, Fermat's theorem, Chinese Remainder Theorem, Higher Residual Theory, and other essential theories are extensively applied in contemporary secure communication, digital signature, identity authentication, and related fields. Thus, gaining a profound understanding of the workings of these encryption systems is crucial for advancing information technology and has the capacity to foster the creation of novel ways or strategies in information security.

2 Cipher and Virginia Ciphers

Cipher encryption, one of the oldest method of data encryption, is a shift cipher, and encrypts data by substituting characters that are "x" numbers of characters ahead in the alphabet for the original letters [2]. For instance, if we shift each letter in cleartext by three to the right in alphabet, then we have,

\( A↦D,B↦E,C↦F,…,Z↦C \)

The message \( ESCAPE \) is encrypted as \( HVFDSH. \)

2.1 Caesar cipher

The encrypted message \( XKFJXI \) is decrypted by shifting three letters to the left, and we get \( ANIMAL. \)

The process shown above is the Caesar Cipher, an encryption method by shifting a fixed amount. Now, if we combine the number theory with Caesar Cipher, it is obvious that the whole process is the addition by a fixed number modulo 26, which means that the encryption function can be written as

\( E(x)=x+3 mod 26 \)

and the decryption function can be expressed as

\( D(y)=y-3 mod 26 \)

What needs to be mentioned is that if we write a general encryption function for Caesar Cipher, which is

\( E(x)=ax+b mod 26, wheregcd{(a,26)}=1 \)

Caesar Cipher only considers \( a=1 \) , and we can change the value of a to make the encryption system more complicated.

Consider the function \( E(x)=5x+3 mod 26 \) .

Then, by substituting \( x=1,2,3,4… \) , we can obtain \( A↦H,B↦M,…,Z↦C \) .

This general function is called affine transformation, and shift transformation (Caesar’s method) is the special case when a=1. Thus, as x traverses the complete residue system of module 26, the value of E(x) similarly traverses. There are \( ∅(26)=12 \) choices for a because a is coprime with 26, while b has 26 choices. Therefore, there are 312 types of such affine transformation.

If we want to decrypt the encrypted message, the first step is to correspond the most frequently occurred letters in the encrypted information and those in normal writing. So, if the transformation is expressed in the form of \( C≡aP+b mod 26 \) , what we need to do is substituting the corresponding letters into the equations and find the solution of the modulo equation, as shown in figure 1.

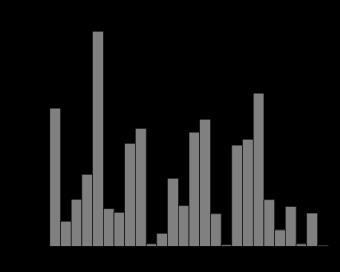
Figure 1. The frequency of each letter in the English alphabet (Source: Wikipedia)

The Caesar cipher can be enhanced by incorporating matrices and vectors instead of basic linear functions, resulting in a more advanced encryption method known as a block cipher. This approach allows for the manipulation of several letters simultaneously. We can use a 2-letter block and 2 \( × \) 2 matrices as an example.

The information we want to encrypt is \( DOODLE \) , and it becomes three sets that have 2 letters in one set \( DO OD LE \) .

Then, we can write each set into vectors of numbers mod 26 (A=1, B=2 and so on)

\( (\frac{D}{O})=(\frac{4}{15}),(\frac{O}{D})=(\frac{15}{4}),(\frac{L}{E})=(\frac{12}{5}) \)

We randomly pick a 2 \( × \) 2 matrix with numbers mod 26, for example

\( Α=(\begin{matrix}3 & 2 \\ 1 & 11 \\ \end{matrix}) \)

In order to encrypt the blocks above, we just multiply them with the matrix chose randomly and take mod 26.

\( A(\frac{4}{15})=(\frac{16}{13}) \)

\( A(\frac{15}{4})=(\frac{1}{7}) \)

\( A(\frac{12}{5})=(\frac{20}{15}) \)

Then, transfer the vectors above back to letters and we will obtain the encrypted information, which is PMAGTO.

To summarize, the Caesar cipher is an encryption scheme of historical significance that involves a fixed number of alphabetic shifts. Despite its simplicity and ease of use, the Caesar cipher is not suitable for ensuring secure communication in modern contexts due to many inherent weaknesses. Brute-force assaults can quickly decrypt the Caesar cipher, especially in today's constantly advancing technological culture. An attacker can readily interpret the message by exhaustively attempting all conceivable combinations, considering that there are only 25 potential shift values (excluding the case of no shift). Nevertheless, the straightforwardness of the Caesar cipher renders it an effective instrument for teaching purposes and a suitable beginning topic for novices to explore.

2.2 Virginia cipher

Virginia cipher is often regarded a derivative of Caesar cipher, but it is more complicated and harder to decrypt. The secret key of Virginia cipher is a keyword:

\( l_{1}l_{2}l_{3}…l_{n} \)

The function of this keyword (secret key) is to encrypt the cleartext by some operations based on number theory. Then, the equivalence value of \( l_{1}l_{2}l_{3}…l_{n} \) is \( k_{1}k_{2}k_{3}…k_{n} \) . In order to encrypt the cleartext, we first separate it into groups of letters which have the length of n.

After transforming the cleartext into equivalence value, we need to use affine cipher to output the decrypted text \( c_{1}c_{2}c_{3}…c_{n} \) , and it is expressed by \( c_{i}≡p_{i}+k_{i} mod 26 (0≤c_{i}≤25) \) .

For instance, if the key word is YTWOK, and we want to utilize Virginia cipher to encrypt the cleartext MILLENIUM.

First of all, we need to transform cleartext and keyword into equivalence value.

\( p_{1}p_{2}p_{3}p_{4}p_{5}p_{6}p_{7}p_{8}p_{9}p_{10}=12 8 11 11 4 13 13 8 20 12 \)

\( k_{1}k_{2}k_{3}k_{4}k_{5}=24 19 22 14 10 \)

Then, if we apply the Virginia cipher

\( c_{1}=p_{1}+k_{1}=12+24≡10 mod26 \)

\( c_{2}=p_{2}+k_{2}=8+19≡1 mod26 \)

\( c_{3}=p_{3}+k_{3}=11+22≡7 mod26 \)

\( c_{4}=p_{4}+k_{4}=11+14≡25 mod26 \)

\( c_{5}=p_{5}+k_{5}=4+10≡14 mod26 \)

\( c_{6}=p_{6}+k_{1}=13+24≡11 mod26 \)

\( c_{7}=p_{7}+k_{2}=13+19≡6 mod26 \)

\( c_{8}=p_{8}+k_{3}=8+22≡4 mod26 \)

\( c_{9}=p_{9}+k_{4}=20+14≡8 mod26 \)

\( c_{10}=p_{10}+k_{5}=12+10≡22 mod26 \)

Therefore, the decrypted text is KBHZO.

Friedman described a method to figure out the frequency of repeated strings. For any given string with n characters \( x_{1}x_{2}x_{3}…x_{n} \) , and let IC represents the repeated times, and IC means the probability of randomly choosing two same elements from the string.

Now, we assume that the frequency of occurrence in the string of letters A, B, …, Z is \( f_{0},f_{1},f_{2}…f_{25} \) . Since the \( i_{th} \) letter appears \( f_{i} \) times, which means that there are

\( (\frac{f_{i}}{2})=\frac{f_{i}(f_{i}-1)}{2} \)

ways to choose 2 elements that are both the \( i_{th} \) character. Then, since there are \( (\frac{n}{2})=\frac{n(n-1)}{2} \) ways to choose 2 characters in the whole string, we can deduce that

\( IC=\frac{\sum_{i=0}^{25} f_{i}(f_{i}-1)}{n(n-1)} \)

The Virginia encryption algorithm employs a keyword-based encryption strategy. The encryption process involves utilizing a keyword to encrypt plaintext. The number of Caesar cipher tables used for encryption is determined by the length of the keyword. The procedure establishes a correlation between the keyword and the plaintext, which is then employed for the purposes of encryption and decryption.

The Virginia cipher wheel and algorithm, while offering improved security compared to the basic Caesar cipher, may still have vulnerabilities to certain traditional cryptographic attacks. Modern cryptography employs intricate encryption methods that are grounded in mathematics, as they provide enhanced levels of protection.

3 RSA Encryption System

Prime numbers are a fundamental notion in elementary number theory and were widely examined in ancient Greece. Ancient Greek scholars conducted extensive investigations into prime numbers, uncovering numerous fundamental features and notably establishing the renowned Fundamental Theorem of Arithmetic. The renowned Fundamental Theorem of Arithmetic serves as the foundation and initial concept of elementary number theory [3].

Prior to 1977, the interest in the decomposition of big numbers was mostly driven by pure mathematical study. Subsequently, following the introduction of the public key system, three youthful researchers affiliated with the Computational Science Laboratory at the Massachusetts Institute of Technology (MIT), namely Rivest, Shamir, and Adleman, capitalized on the challenge of factoring large numbers and collaborated to propose a public key scheme. This scheme is now recognized as the RSA public key encryption system [4]. The RSA cryptosystem is a public-key cryptosystem based on modulo powers, where the key is a pair of numbers (e, n) generated from power of e and the product of two big prime numbers modulo n. This means that \( n=pq \) where p and q are big prime numbers, and \( (e,φ(e))=1 \) . In order to encrypt the text, we first transform the letters into equivalence value and try to form data groups (have even digits) as long as possible name them as cleartext groups P.

Then, using the equation below to encrypt P into ciphertext groups C:

\( E(P)=C≡P^{e} mod n, 0≤C \lt n \)

Conversely, the process of decryption requires the inverse of e modulo \( φ(e) \) , which is d. Since \( (e,φ(e))=1 \) , the inverse d must exist. The function of decryption can be expressed as:

\( D(C)≡C^{d}=(P^{e})^{d}=P^{de}=P^{kφ(n)+1}≡P(P^{φ(n)})^{k}≡P mod n \)

In the equation, \( de= kϕ(n)+1 \) where k is a integer, and we have \( P^{ϕ(n)}≡1 mod φ(n), \) so the number pair (d, n) is the decryption key.

For instance, now we are using RSA system to encrypt the plaintext:

PUBLIC KEY CRYPTOGRAPHY

We assume the large prime numbers we choose is 43 and 59 and take e=13 as power. In this case, \( n=43×59=2537 \) . Here, \( (e,φ)=(13,42∙58)=1. \)

First, we need to transform the letters into equivalence value, and in this example, we put those numbers in groups with 4 numbers each. They are:

1520 0111 0802 1004

2402 1724 1519 1406

1700 1507 2423 (this 23 is the added filling number)

Then, we use the equation mentioned above, which is

\( C≡P^{13} mod 2537 \)

If we want to encrypt the fisrt group of numbers:

\( C≡1520^{13}≡95 mod 2537 \)

Therefore, the whole cleartext is encrypted into:

0095 1648 1410 1299

0811 2333 2132 0370

1185 1957 1084

If we want to decrypt the text using RSA system, the first step is to find the inverse for e=13 modulo \( ϕ(n)=2436 \) . By using the Euler Algorithm, we can obtain that d=937.

So, we can use the equation below to decrypt the text:

\( P≡C^{937} mod 2537, 0≤P \lt 2537 \)

To sum up, we can consider the security of RSA Cipher System. There is no doubt that any individual can find a huge prime number with 100 digits in just several minutes by using computer. These prime numbers can be found by randomly choosing odd numbers with 100 digits since the theorem of prime numbers claims that the probability to get such a prime number is about \( \frac{2}{log{10^{100}}} \) . As soon as we found out the two huge prime numbers, we can just a larger prime number to be the power e. What makes RSA very secure is that if we want to find the inverse of e modulo \( ϕ(n) \) , the first thing to do is to calculate \( ϕ(n)=ϕ(pq)=(p-1)(q-1) \) , but it is extremely hard to find \( ϕ(n) \) since the relationship between p, q and n are uncertain and p and q have 100 digits. Even though using the most advanced computer takes millions of years to solve p and q. However, M. Wiener found one weakness of RSA, and he stated that when n=pq and if q \( d \lt \frac{n^{1/4}}{3} \) [5].

RSA is considered secure due to the difficulty of factoring large semiprime numbers into their prime factors. The security of RSA is directly influenced by the length of the key. While longer keys provide enhanced security, the encryption and decryption processes become more time-consuming as the key length increases. As processing power increases, it is recommended to use longer keys in order to maintain security.

4 Conclusion

This paper provides an overview of the number theory behind various encryption methods and enumerates numerous practical applications of number theory in encryption. During this procedure, readers might develop an instinctive understanding of the benefits and drawbacks associated with various encryption techniques. Simultaneously, we acknowledge the strong correlation between number theory and cryptography. It is evident that the procedures of encrypting, decrypting, deciphering, and sharing passwords are intertwined with the understanding of number theory. Consequently, number theory cryptography has emerged as the prevailing field within cryptography.