1. Introduction

A subfield of mathematics called probability theory studies the quantity law governing random processes. Random phenomena are the reverse of deterministic phenomena, which are certain to occur based on predetermined conditions. The random phenomenon occurs when a researcher observes something under the identical conditions but is unable to predict the outcome and will occasionally surface. Probability is the likelihood that something will occur under certain circumstances. One thing will happen occasionally in a test taken only once, but when the test is taken many times, it tends to show up in a noticeable way [1]. The 16th century saw the invention of probability theory by Italian academic Girolamo Cardano, who used it to study gambling games. After discovering that probability theory could be applied to a variety of domains, including biological, physical, and social phenomena, through human social practice, it evolved into a legitimate topic of study. A key concept in probability theory is the random walk.

A notable example of the application of random walks is the “Gambler’s Ruin,” which uses a random walk model to determine how gamblers lose their money. Roulette is a popular game at gambling establishments. A player can play for one dollar and has a 47.3% chance of winning. If a player wants to bet more money and return home, he can only do so if \( n=100 \) and \( m=100 \) . Another example is “drunk walking,” where a drunk person walks down the street. They have a 50/50 chance of going right or left after a few minutes, so where can they find the drunk person in an hour? The third example—also known as Brownian motion—is something that most people hear about in middle school [2]. In the final example, a lot of people use the internet. When people visit a website, they have the option to verify, and their choices are also random. Similarly, on the next page, people are randomly assigned to an option.

The random walk with Brownian motion will be introduced in the following Section 2. Next, Section 3 will cover point three applications of the random walk, and each will conclude with a recap. The paper will be summarized in the final Section 4.

2. Methods and theory

A random walk indicates that the past performance is not indicative of future process development or direction. The fundamental idea is that every conserved quantity that an irregular walker carries is equivalent to a diffusion transport law. A random walk is the best mathematical state of Brownian motion and the most basic Brownian model. Random walks and Brownian motion are closely linked concepts. Random walks are a popular tool for drawing findings in a variety of fields, including financial stock market analysis and internet link analysis [3].

Different dimensions of random walks share the same architecture. In dimension two, for example, a random walk has a locus that is two-dimensional random and moves to its adjacent point with equal probability every predetermined amount of time. To give a basic example, one can place a pen on the paper and give the test-taker two coins. With coin 1, they must decide whether to move forward or backward, and with coin 2, they must choose to move left or right. The test-taker will toss two coins every three seconds; if coin 1 is in the front, the pen will move forward; if coin 2 is on the back, the pen will go left. The pen will write two-dimensional random walking on the paper. It is interesting to know if there is a chance the pen will return to its original place if coins are thrown a thousand times. The coin must therefore have 500 heads and 500 tails. A list of positive numbers will be rolled for a specific slot sequence, which consists of 500 different integers. This quantity is, and arbitrarily two sequences only have the element Change order exist, but in practice didn’t have different, so they must divide the number that is likely to be replaced by 500 [4].

Suppose that \( {M_{0}} \) denotes the mode that can return to the starting point, and the probability that the pen can do so is \( {P_{0}} \) , which can satisfy the binomial distribution. Stirling’s method can be used to evaluate all \( M \) possibilities. Based on the calculations, people may conclude that there is a very small chance that they will end up back where the thing is started. The optimum state of Brownian motion is a random walk; different systems have different types of random walks, but they all have similarities. While a single random event is unpredictable, one can exactly forecast a vast number of random events, which is how the random walk comes to be [5]. According to probability, randomness in low dimensions creates disagreement, whereas in large dimensions, it creates similarity. The total probability of all random events is represented by a suitable formula.

3. Results and Application

3.1. Multi-particle random walk immune algorithm

The random walk approach focuses on weak nodes in the network, while the algorithms for getting network global information and network end centrality based on degree centrality are challenging but complex. Based on the multi-particle random walk immune (RWI) algorithm, people no longer need to obtain global information in order to reach the transmission range. First, the random walk algorithm is selected to carry out a multi-particle walk on the network and obtain the nodes with high traffic according to the traffic ranking. Suspected-infected-recovered (SIR)/removed and suspected-infected transmission experiments were performed using classical immunization strategies on eight real datasets [5]. Second, propagation verification was done using wandering screened nodes to conduct suspected-infected (SI) and SIR propagation experiments. The method’s viability and validity were shown by comparing it to numerous other immunization techniques.

Based on the experimental results of the RWI method in various network models and propagation models, the influence of node degree centrality and location information on the time of outward range and propagation outbreak is considered thoroughly. On one thing, the structural features of real networks differ from those of an undirected powerless network. In the case of the community obvious network, nodes at the community’s edge are crucial to network propagation because they can effectively stop the network community from spreading. This indicates the importance of the RWI algorithm in guiding the propagation of reality. On another thing, it can be observed from the side that the node propagation ability is not only affected by the node degree value; when controlling the propagation of the network, the location information of the node should also be fully considered. The node based random walk algorithm has higher accuracy for finding such nodes, and the results of the multi-particle random walk experiment show that it is affected by communication mechanisms and network structure. There are some differences in degree centrality and network location of nodes [6].

Last but not the least, RWI has a lower time complexity and a wider variety of applications compared to other random errands based on network edge and the algorithm of the transfer control ability of the nodes in the center of the intermediate number center. In order to give a novel idea for the future propagation control of complex networks, this study creatively integrates the immune algorithm with the random walk notion. The efficacy of the algorithm is proven in several application scenarios, and propagation experiments are conducted on a variety of real data sets. Figure 1 shows the time percentage stacking chart of the RWI and TI_BC in different network [7].

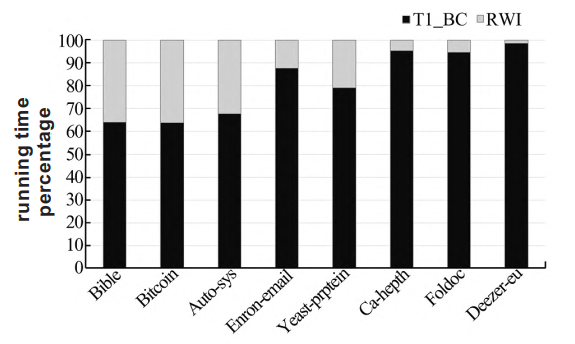
Figure 1. RWI and TI_BC in different network running time percentage stacking chart [5].

3.2. Density peak clustering algorithm based on random walk

The density peak clustering (DPC) algorithm uses Euclidean distance to define local density and relative distance because it is based on local density and relative distance. As a result, some sparse and large differences and long arcs have an unfavorable clustering effect, and some coordination strategies are not reliable [8]. This work presents a density peak clustering algorithm based on random walk (RW-DPC), which redefines the local density of data points and uses a random walk to describe the similarity between them in order to reach the model.

Additionally, a new sample allocation strategy is proposed, and the clustering effect of the proposed algorithm is compared with the experimental results of other clustering algorithms on the artificial data set and the real data set from University of California, Irvine. The results demonstrate that the database of uneven density and curved class outperforms both the density peak clustering algorithm and other algorithms. This algorithm can accurately reflect the distance between data points when the dataset’s data distribution structure is complex. People solve the issue of different data points distributed in different clusters, and have stronger robustness when used in place of the less-than-ideal density peak clustering algorithm. Numerous tests were carried out, and when compared to other algorithms, the results indicate that RW-DPC has a better clustering impact on a variety of data sets than other methods.

3.3. Community discovery methods based on random walks

Communities can find information more quickly and accurately thanks to random walk technology. The random walk-based community discovery method is analyzed and summarized, and it is further divided into two categories of tasks: local community discovery and global community discovery. Personalized page ranking methods, heat and diffusion methods, and other random walk methods are among the subdivided methods [9]. The challenges are examined, the future research direction is suggested, and the use of various random walk types in these two categories of community finding tasks is described in depth.

Lastly, there are two key points that sum up the community discovery accuracy evaluation indexes: In order to aid pertinent study, there are two criteria: similarity and structure. In order to examine the topology structure and evolution process of complex networks, community discovery is a fundamental technique that seeks to determine the community structure of a network. Local community discovery in this research is classified into two categories: high-level local community discovery and local community discovery based on the network’s initial topology.

3.4. Interactive image segmentation based on random forest and random walk

An improved method of symmetric detection based on random forest is proposed, taking advantage of the heap structure that is widely present in the image. As a result, the difference between the quality of adjacent pixels and the interactive image segmentation based on random walk is only taken into consideration when there is a color space difference [10]. Symmetry detection becomes an organized labeling challenge when features with similar edges are used. In order to increase the accuracy of interactive segmentation, the expectation maximum algorithm establishes the relationship between the symmetry axis and the neighboring pixels based on the symmetry axis. The outcome of the experiment indicates that the approach outperforms the current interactive random walk-based image segmentation technique in terms of accuracy. It is possible to produce highly precise results for interactive segmentation using this method, in addition to effectively extracting the image’s symmetry axis.

4. Conclusion

The random walk, which is a walk based on the previous step, is the main topic of this paper. It also discusses the philosophy behind the random walk. In addition, a few instances are provided, such as the internet’s utilization of random walks, Brownian motion, drunk walking, and the gambler’s Ruin. Based on a multi-particle random walk immune technique, this application in some academic settings uses interactive image segmentation based on random walk and random forest, which refers to many people’s lives or social interactions. While it is evident that winning at a bet is extremely difficult, readers of Gambler’s Ruin can learn what is achievable in a gambling party. On the other hand, Brownian motion can be known in the physical world. Thus, random walks are crucial and play a significant role in probability theory. This study aims to demonstrate the random walk application, highlight its importance in educating people about random walks, and explore other possibilities for random walks in the future. Some disorderly elements in random walks may require numerous repetitions in order to determine their likelihood.