1 Introduction

Chord progression is like the skeleton of a musical piece. It creates the motion and emotions. While composing a chord progression, to make smooth transitions, one usually requires one chord to progress to the next while keeping some notes in common. For a triad chord, say C major, to write the next chord while keeping two notes in common, one has three choices, i.e. C minor, A minor and E minor.

Definition 1.1. There are three basic transformations of triads:

1 P transformation: a chord is transformed to its parallel. So it changes the tonality and keeps the root.

2 R transformation: a chord is transformed to its relative. So it changes the tonality and moves the root by a minor third.

3 L transformation: the remaining transformation. So it changes the tonality and moves the root by a major third.

We understand PLR transformations as a way of measuring how “close” two chords are. Every chord is closest to three chords. Every two chords are connected by a sequence of P, L, R transformations, hence there is a notion of distance.

Represent a triad by an equilateral triangle labelled at vertices by its constituent notes. We can then draw its PLR transformations as three adjacent labelled equilateral triangles, since they all have two notes in common. Continuing this way, the graph is extended to the whole plane, called the Tonnetz graph:

Figure 1. Taken from Neo-Riemannian theory, wikipedia.

Two periodic occurrences are recognized in the pattern: one is the translation in the direction of major third by 3 (i.e. an octave), the other is the translation first in the direction of minor third by 1, then in the direction of fifth by 3 (together two octaves). It is then natural to identify points that differ by a period. This is exactly how topologists produce a torus!

The relations among the 12 notes and 24 triads are thus perfectly exhibited on a torus. Chord progressions from many pieces have been animated in this framework. For example, in Beethoven’s 9th Symphony, 2nd movement, measures 143-176, he wrote the following 19 chords in a row:

\( C,Am,F,Dm,B^{♭},Gm,E^{♭},Cm,A^{♭},Fm,D^{♭},B^{♭}m,G^{♭},E^{♭}m,B,G^{♯}m,E,C^{♯}m,A. \)

This was well-crafted, as an alternative sequence of R and L applied to the initial one (see figure 2):

Figure 2. Taken from example 31.14a, [1].

Following this pattern if we add at the end 5 more chords \( F^{♯}m,D,Bm,G,Em \) , we get all of the 24 triads. On the Tonnetz torus, this progression traces a loop that wraps three times around the latitude circle.

We can also analyze a progression in terms of compound transformation. For example, the classical Pachelbel’s Canon progression is broken down as

\( IVviiiiIVIIVV. \)

Since PLR are all involutions, their compositions form a group (as a subgroup of the symmetric group \( S_{24} \) ), called the PLR group. The following result might not be known to music theorists:

Theorem 1.2. The PLR group is a free and transitive subgroup of \( S_{24} \) , isomorphic to the dihedral group \( D_{12} \) .

In John Baez’s column This Week’s Finds in Mathematical Physics [2], week 234, he proposed a new model to do musical analysis, in relation to the Klein quartic curve:

Figure 3. Picture by Greg Egan.

The Klein quartic curve is an algebraic curve in \( P^{2}(C) \) defined by

\( x^{3}y+y^{3}z+z^{3}x=0. \)

It is “as symmetric as possible” among smooth quartic curves. The figure 3 above shows a triangulation of the curve, with 24 vertices, 84 edges and 56 faces. The underlying space is a 3-holed torus. It has a 168-fold symmetry.

Proposition 1.3. The automorphism group \( G \) of Klein’s quartic is the second smallest non abelian simple group, of order 168. We have \( G≅PSL(2,7)≅PSL(3,2) \) . It acts transitively on the set of vertices / edges / faces of the triangulation. It has the presentation

\( G=⟨x,y|x^{2},y^{3},(xy)^{7},[x,y]^{4}⟩. \)

There are 6 conjugacy classes, represented by \( e,x,y,[x,y],xy,(xy)^{-1} \) , of size 1,21,56,42,24,24 respectively.

In this paper, we invent a way of labeling the 24 vertices by the 24 triads, which is of interest both musically and mathematically. This is a generalization of the Tonnetz graph, and we will do a harmonic analysis very much like that of Beethoven’s 9th Symphony.

The rest of the paper is organized as follows. Section 2 is on the interplay between maths and music. After a preliminary introduction written for non musicians, we discuss how the works of Bach and Messiaen are related to group theory and topology. In section 3, we discuss various groups and spaces that show up in a musical context. These two sections are mostly a survey of mathematical music theory. Nevertheless, there are some works not in the literature. We give a rigorous proof of Messiaen’s claim on the modes of limited transposition, and we describe an action of the icosahedral group in music. Our main original result is in section 4. We give a characterization of Klein’s quartic based on hyperbolic geometry, then use its platonic tessellation to construct a new model to do harmonic analysis. We comment on our new model and illustrate it with an application at the end.

2 Maths and music

2.1 From music to mathematics

The modeling of 12-tone music is based on simple maths. First, a pitch is determined by its frequency in hertz, which is a positive real number. For example, the middle A on the piano (A4) is 440 Hz.

By Fourier analysis ([3], section 1.1), if the A4 is played, one simultaneously hears the hidden frequencies 880 Hz, 1320 Hz, 1760 Hz, etc. In general, a pitch X of frequency \( x \) always comes with a harmonic series \( Nx \) , \( N=1,2,⋯ \) . If X and A4 are played at the same time, our ears perceive a sense of consonancy that is dictated by how much the two harmonic series overlap. The more they overlap, i.e. the closer \( x:440 \) is to a simple integer ratio, the more consonant it is to our ears. This is the basic principle of harmony.

The simplest integer ratio relation is \( x:440=2:1 \) , then X is said to be an octave higher than A4, i.e. the frequency doubles. This is the most consonant. A note is an equivalence class of pitches under octaves. For example, the note A represents \( {2^{k}⋅440|k∈Z} \) .

Within an octave, the simplest ratio is 3:2. This is the perfect fifth interval. Then we have this numerical coincidence:

\( 3^{12}/2^{19}≈1.01. \)

Thus we can iteratively use 3:2 to generate new notes, and we stop at \( (\frac{3}{2})^{12} \) , pretending that it is \( 2^{7} \) . This process gives us 12 notes within an octave, called Pythagorean tuning. It is an approximation of the 12 equal temperament

\( 1,2^{\frac{1}{12}},⋯,2^{\frac{11}{12}},2. \)

Remark. Consider dividing an octave into a geometric sequence while trying not to miss the perfect fifth, mathematically we are doing the rational approximation of log \( _{2}\frac{3}{2} \) . There is an algorithm using continued fraction ([4], section 6.3):

\( log_{2}\frac{3}{2}=\frac{1}{1+}\frac{1}{1+}\frac{1}{2+}\frac{1}{2+}\frac{1}{3+}\frac{1}{1+}\frac{1}{5+}⋯ \)

Truncate it at the 4th term, we get \( \frac{7}{12} \) . This recovers the previous coincidence. The next truncation would be \( \frac{24}{41} \) . So there is also a reasonable 41 equal temperament system music, known as a kind of microtonal music.

In composition, one usually does not use all of the 12 notes. One typically uses 7 of them, called a scale (though a scale can also have more or less notes). For example, the C major scale contains the notes C, D, E, F, G, A, B, with C chosen as the tonal center, meaning that C is like “home”. We introduce the 12 notes according to their relation to C:

Definition 2.1. The smallest interval among the 12 notes is called a semitone. An octave contains 12 semitones. In the C major scale:

• C is called the tonic.

• D is called the supertonic. It forms a major 2nd (i.e. 2 semitones) above C.

• E is called the mediant. It forms a major 3rd (i.e. 4 semitones) above C.

• F is called the sub-dominant. It forms a perfect 4th (i.e. 5 semitones) above C.

• G is called the dominant. It forms a perfect 5th (i.e. 7 semitones) above C.

• A is called the sub-mediant. It forms a major 6th (i.e. 9 semitones) above C.

• B is called the leading tone. It forms a major 7th (i.e. 11 semitones) above C.

• C \( ^{♯} \) =D \( ^{♭} \) forms a minor 2nd (i.e. 1 semitones) above C.

• D \( ^{♯} \) =E \( ^{♭} \) forms a minor 3rd (i.e. 3 semitones) above C.

• F \( ^{♯} \) =G \( ^{♭} \) forms a tritone (i.e. 6 semitones) above C.

• G \( ^{♯} \) =A \( ^{♭} \) forms a minor 6th (i.e. 8 semitones) above C.

• A \( ^{♯} \) =B \( ^{♭} \) forms a minor 7th (i.e. 10 semitones) above C.

The chromatic scale refers to the scale made of all the 12 notes.

It is natural to model the 12 notes by the cyclic group \( Z/12 \) , with 0=C, 1=C \( ^{♯} \) =D \( ^{♭} \) , etc.

Definition 2.2. Let \( x∈Z/12 \) represent a note X, chosen as the tonal center.

• The X major scale consists of the 7 notes \( x+{0,2,4,5,7,9,11} \) .

• The X minor scale consists of the 7 notes \( x+{0,2,3,5,7,8,10} \) .

Example. The A minor scale is A, B, C, D, E, F, G, called the relative scale of C major, for they contain the same notes (but different tonal centers). The C minor scale is C, D, E \( ^{♭} \) , F, G, A \( ^{♭} \) , B \( ^{♭} \) , called the parallel scale of C major, for they have the same tonal center.

Harmony in an elementary level is written in terms of triad chords, which are three notes played at once that sound reasonably consonant. Recall that the most consonant interval between different notes is the perfect 5th. Insert one more note in between, we get a triad. According to whether this note with the lowest note in the triad (called the root) forms a major 3rd or minor 3rd, we call it a major triad or minor triad. Musically, they create a contrast in emotions, as do major scale and minor scale.

Definition2.3. Let \( x∈Z/12 \) represent a note X, as the root.

• The X major chord consists of the 3 notes \( x+{0,4,7} \) . We denote it by \( x^{+} \) or X.

• The X minor chord consists of the 3 notes \( x+{0,3,7} \) . We denote it by \( x^{-} \) or X \( _{m} \) .

Example. The C major scale (also the A minor scale) contains 3 major chords: C, F, G; and 3 minor chords: Dm, Em, Am.

While \( x \) ranges over \( Z/12 \) , we get 24 major or minor triads. The transformations P, L, R as defined in .1 permute them. We are now ready to give a proof of theorem 1..

Proof: We use a graphic presentation well known to musicians, called the circle of fifth:

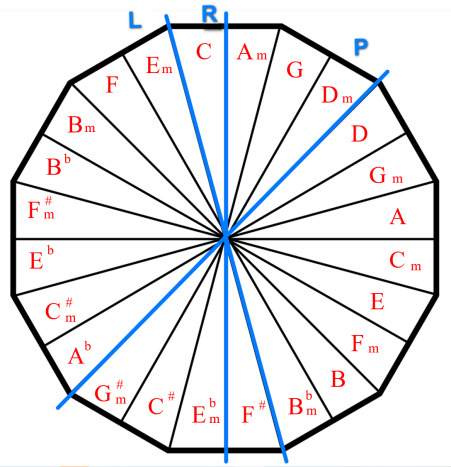We redraw it on the barycentric subdivision of a regular dodecagon, but with the direction of minor chords reversed. The P, L, R are thus realized as three reflections in \( D_{12} \) . Since \( R∘L \) is a rotation by \( \frac{π}{6} \) , which with \( P \) generates \( D_{12} \) , the PLR group is isomorphic to \( D_{12} \) . It is free and transitive, since the triads form one single orbit of maximal size 24.

2.2 From mathematics to music

To give an example of sophisticated maths actually applied to musical composition, we mention the works of the French composer Olivier Messiaen (1908-1992). The first distinction of his composition is that, instead of writing in the usual major or minor scale, he invented what he called modes of limited transposition to write music. To explain this terminology, note that taking the 7 notes in the C major scale but altering the tonic yields 7 different scales. We say that the C major scale has 7 modes: C-Ionian, D-Dorian, E-Phrygian, F-Lydian, G-Mixolydian, A-Aeolian (i.e. A minor) and B-Locrian. Simply by changing the tonal center, these scales that share exactly the same notes have totally different vibes. Another way of saying this is that the C major scale has full transposition, meaning that the maps from \( Z/12 \) to itself defined as

\( T_{n}:x↦x+n, n∈Z/12 \)

send the C major to 11 other scales, none of them has the same notes as the C major.

What are the scales that do not have this property? A prominent example, made famous by Debussy, is the whole-tone scale: C, D, E, F \( ^{♯} \) , G \( ^{♯} \) , A \( ^{♯} \) , or \( {0,2,4,6,8,10} \) . Picking any of the six as the tonal center, the music gives the same feeling. This creates a sense of ambiguity, that some composers want to manipulate in their pieces.

The whole-tone scale is also known as Messiaen’s 1st mode of limited transposition. It has only 2 transpositions, so it is “limited”. Others on his list are:

• Messiaen’s 2nd mode: \( {0,1,3,4,6,7,9,10} \) , 3 transpositions.

• Messiaen’s 3rd mode: \( {0,2,3,4,6,7,8,10,11} \) , 4 transpositions.

• Messiaen’s 4th mode: \( {0,1,2,3,6,7,8,9} \) , 6 transpositions.

• Messiaen’s 5th mode: \( {0,1,2,6,7,8} \) , 6 transpositions.

• Messiaen’s 6th mode: \( {0,2,4,5,6,8,10,11} \) , 6 transpositions.

• Messiaen’s 7th mode: \( {0,1,2,3,4,6,7,8,9,10} \) , 6 transpositions.

Messiaen claimed that this list was mathematically complete. We state and prove his claim.

Proposition 2.4. After transposition, a proper subset \( S \) of \( Z/12 \) such that \( T_{n}⋅S=S \) for some non trivial \( T_{n} \) must be contained in the 7 Messiaen’s modes.

Proof: Assume \( 0∈S \) . Note that \( {n|T_{n}⋅S=S} \) forms a non trivial subgroup of \( Z/12 \) . So \( {n|T_{n}⋅S=S}≅Z/d \) , \( d=2,3,4,6 \) . In each case, there are \( \frac{12}{d} \) transpositions. The action of \( Z/d \) on the 12 notes has \( \frac{12}{d} \) orbits, and \( S \) is determined by a proper subset of the set of orbits. We only discuss the maximal scales (in each case there are \( \frac{12}{d}-1 \) of them), and show that they are transpositions of Messiaen’s modes.

4 \( d=6 \) , \( S \) must be \( {0,2,4,6,8,10} \) (the 1st mode).

5 \( d=4 \) , \( S \) is \( {0,1,3,4,6,7,9,10} \) (the 2nd mode) or \( {0,2,3,5,6,8,9,11}=T_{2}⋅{0,1,3,4,6,7,9,10} \) .

6 \( d=3 \) , \( S \) is the 3rd mode or its \( T_{1} \) , \( T_{2} \) .

7 \( d=2 \) , \( S \) is the 7th mode or its \( T_{2} \) , \( T_{3} \) , \( T_{4} \) , \( T_{5} \) .

Note that the 7th mode contains the 4th, which further contains the 5th. The 7th also contains \( T_{2} \) of the 6th.

In his piano piece Ile de feu 2 Messiaen employed more mathematical tricks. To unravel this piece, we introduce first the usual motif development techniques in composition. A motif is usually a short melody line with simple rhythm. To develop it and also to keep reminding the audience of it, composers consistently let it appear throughout the piece, but with variations. Sometimes the motif is repeated in a different voice part, on a different instrument. So the pitch changes, but the rhythm is mostly kept. There are two basic types of variation that can be applied to a melody line:

• Transpositions \( T_{n} \) ( \( n∈Z/12 \) ), as defined previously. They just translate a melody higher or lower.

• Inversions \( I_{n}:x↦n-x \) , ( \( n∈Z/12 \) ). They turn everything (e.g. intervals, chords, emotions) upside down.

It is easy to see that the 12 transpositions and the 12 inversions form a dihedral group \( D_{12} \) . The motif development is modeled by this \( D_{12} \) -action on a sequence of elements in \( Z/12 \) .

Example. Bach as the representative, the counterpoint writing in Baroque music makes extensive use of this \( D_{12} \) -action (see [5], section 1.4). Bach’s style has the reputation of being highly rational and maths-like.

Example. Schoenberg had his serialism philosophy, that he would pick any permutation \( (a_{i})_{i=1}^{12} \) of elements in \( Z/12 \) (called the tone row), and form the 12-tone matrix

\( a_{ij}=a_{1}+a_{j}-a_{i}, 1≤i,j≤12. \)

The rows are all the transpositions of the tone row, and the columns are all its inversions.

Theoretically, one could use any subgroup of \( S_{12} \) to generate variations of motif. An interesting subgroup is the Mathieu group \( M_{12} \) , which is one of the 26 sporadic finite simple groups. As a subgroup of \( S_{12} \) , it is generated by the two so-called Mongean shuffles ([4], section 9.16)

\( a=(\begin{matrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 7 & 6 & 8 & 5 & 9 & 4 & 10 & 3 & 11 & 2 & 12 & 1 \\ \end{matrix}) \)

\( b=(\begin{matrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 6 & 7 & 5 & 8 & 4 & 9 & 3 & 10 & 2 & 11 & 1 & 12 \\ \end{matrix}) \)

and is of order 95040. There was no evidence that Messiaen knew this group \( M_{12} \) but, in Ile de feu 2, he was consciously using these two permutations \( a \) and \( b \) to generate new variations. See[6] , page 411 for a musical score.

2.3 A topological prelude

Although the Tonnetz torus from neo-Riemannian theory was not formulated and widely studied until the 20th century, there was already an unexpected connection to topology lurking in the work of Bach from the 18th century.

Figure 4. The fifth canon from BWV 1087.

Bach greatly promoted the composition style called canon. A canon is roughly a 2-part harmony, in which the second part, not only accompanies the melody line harmonically, but also imitates the melody with slight delay. So the audience hears a mixture of repetition and variation in the music. The hard thing is to find variations of the first part that also make sense harmonically when played slightly after it. What was even more extraordinary about Bach’s genius was that he could also write a so-called “crab canon”, in which the second part was literally the first one retrograded. So he had a melody line, and played it backward, then pieced the two together, and it sounded great.

Another similar trick was found in the canons on the Goldberg ground, BWV 1087, as described in [7]. In the fifth canon, Bach made the second part exactly an inversion (as defined earlier) of the first one, and delayed it by 2 measures. It was almost like a mathematical puzzle. If we twist the sheet music in a way that the second line overlaps the first, we make it into a Mobius strip! See the figure 4 above for this process, picture taken from the youtube video Music on a Clear Mobius Strip by Numberphile.

It is fair to say that Bach was essentially composing on a Mobius strip. What is the mathematical reason behind this? In the sheet music, the second line is a reflection of the first, followed by a translation by 2 measures. The mathematical formulation is that the sheet music, recorded on a plane (one dimension for pitch, one dimension for time), has a glide reflection symmetry. We can then record it on the quotient space. And the plane mod out a glide reflection is known as a Mobius strip.

3 Groups and graphic presentations

3.1 Comments on the Tonnetz graph

We have seen in the introduction the basic elements in neo-Riemannian analysis: PLR transformations. They are actions on the set \( S \) of 24 major and minor triads. Consider a graph \( G \) with \( S \) the vertex set, and two vertices are joint by an edge if and only if they are connected by a P, L or R transformation. So \( G \) is a 3-regular graph hence has 36 edges. The induced graph metric defines a notion of distance on \( S \) .

The graph is not a planar graph. It is intuitive to find faces in \( G \) . Consider a fixed note \( x∈Z/12 \) . We easily see that the number of triads containing \( x \) is 6. Moreover, those 6 triads are joint by P, L, R as below in figure 5.

Figure 5. The 6-cycle in \( G \) around \( x \) .

So we define this 6-cycle as a face in \( G \) . Then we have 12 faces in \( G \) , each corresponding to one element in \( Z/12 \) . Thus we have made \( G \) into a 2-complex with 24 vertices, 36 edges and 12 faces. We orient each 6-cycle clockwisely. By computing the Euler number

\( e(G)=24-36+12=0 \)

We see that \( G \) forms a triangulation of the orientable closed surface of genus 1, i.e. the torus. In fact, \( G \) is just the dual complex of the Tonnetz graph in figure . This provides a heuristic argument of why the Tonnetz graph is on the torus.

Though this theory is satisfying from a mathematical perspective, we now analyze its shortcomings in the musical sense. It is reasonable to have the idea that two chords are close if they share the most notes as possible. However, if we measure the closeness according to the tendency of two chords to be adjacent in a progression, we will certainly ignore many important progressions using the PLR formulation since in practice, writing a chord progression is not all about finding common notes and being smooth. We list several important aspects observed from in-practice composition, that we wish to incorporate in our modified theory.

8 Arguably the most important progression is the authentic cadence V - I, from the dominant chord to the tonic chord. Their roots differ by a perfect fifth. They do not have any notes in common, but they do have a strong tendency and a satisfying sound. Since this progression shows up in almost every piece of music, we certainly want to include it as a basic transformation, not a compound one.

9 A different way of writing smooth progressions is to keep the root notes close, commonly by a descending within a whole tone. Though the chords again do not share notes, the progression generally works well because the bass line forms a stepwise motion. It is customarily referred to as half step progression or whole step progression. A typical example is the Andalusian cadence i - VII - VI - V - i, which is a whole step progression followed by an authentic cadence.

10 By far we have mostly considered diatonic progressions, meaning that all the chords are within a same key (i.e. scale). However, tensions and strong emotions are unlikely to be created without non diatonic chords being involved. We would like to include some non diatonic progressions to add more color to the music. Important examples are progressions using the chromatic mediants. For example if we are in the key of C, the usual mediant and sub-mediant chords are Em (i.e. the L transformation) and Am (i.e. the R transformation), and the chromatic mediant chords are \( E^{♭} \) and \( A^{♭} \) . They are borrowed from the parallel key Cm, in the sense that they are just the usual mediant and sub-mediant chords in Cm. The progressions \( CE^{♭} \) and \( CA^{♭} \) both keep one note in common. Chromatic mediants in progressions create a complex texture, and are widely used in especially film scores.

In section 4 we will propose a new model as an analogue of the Tonnetz torus, motivated by these requirements.

3.2 Cube dance

There have been some attempts from other people to modify the PLR formulation. We describe an approach taken by the music theorist Jack Douthett. Acknowledging that a triad is close to its PLR transformations because two out of the three notes do not move, he noticed a mild flaw, that they affect the remaining note differently. Specifically, the P and L transformations shift the remaining note by a semitone, while the R shifts it by a whole tone. So strictly speaking, R is slightly “further” than the other two. Mathematically speaking, Douthett was considering a such distance function on the set \( S \) of 24 triads: for \( A={a_{1},a_{2},a_{3}} \) and \( B={b_{1},b_{2},b_{3}} \) in \( S \) , define

\( d(A,B)=\sum_{i=1}^{3} min_{b∈B}|a_{i}-b|. \)

It is not hard to check that every element in \( S \) has distance 1 to exactly two other elements (i.e. its P and L). By abandoning R and only drawing an edge for a P or L, we obtain a 2-regular graph with vertex set \( S \) . Such a graph must be a disjoint union of loops. Indeed, we have the following (figure 6) 6-cycles in the graph (compare with the Tonnetz graph ):

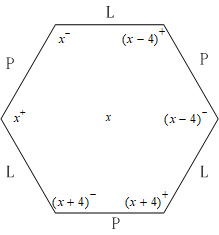
Figure 6. The 6-cycle implying \( (PL)^{3}=id \) .

This cycle contains all the triads with roots congruent to \( x \) mod 4. While \( x \) ranges over 0,1,2,3, the graph is decomposed into four 6-cycles. But this seems rather dull. Moreover, since the graph is disconnected, we can not tell from it the distance between any two triads in different component cycles, e.g. any triad and its R transformation.

The brilliant part is that extra elements can be brought into play. Consider the spaced elements \( (x-4)^{+},x^{+},(x+4)^{+} \) in the cycle. They can all be obtained from shifting by a semitone in the set \( {x-4,x,x+4} \) . Such a triad is not in \( S \) , but it is indeed a less commonly used chord called augmented chord. Note how evenly spaced an augmented chord is, unlike the major and minor chords, we can base the root on any note. There are four augmented triads, rooted at 0,1,2,3. We add a new vertex representing \( {x-4,x,x+4} \) to the graph, and connect it to \( (x-4)^{+},x^{+},(x+4)^{+} \) . Similarly, \( (x-4)^{-},x^{-},(x+4)^{-} \) all have distance 1 to the augmented triad \( {x-5,x-1,x+3} \) . We also add these to the graph. Then see what does the 6-cycle together with the two augmented triads form? A cube! Moreover, these two triads are rooted at \( x \) and \( x-1 \) , it follows that all the 4 cubes are linked head-to-tail. See below (figure 7) for the graphic presentation. Douthett called it cube dance.

It displays perfectly the closeness relations among the 28 chords from the viewpoint of semitone shifting, in the sense that the induced graph metric coincides with the distance function defined previously. It is naturally a 2-complex with 28 vertices, 48 edges and 24 faces, whose underlying topological space is a torus with 4 longitude circles contracted.

We can ask what is its symmetry group \( G \) . By considering the action of \( G \) on the 4 augmented triads, we have a split surjective group homomorphism from \( G \) to the dihedral group \( D_{4} \) . The kernel of it is \( H^{4} \) , where \( H \) is the group of symmetries of cube that fix a pair of antipodal vertices. Equivalently, \( H \) is the group of symmetries of regular hexagon that preserve the two inscribed equilateral triangles. From the latter view we deduce easily that \( H≅S_{3} \) . So \( G \) is a semidirect product of \( D_{4} \) and \( S_{3}^{4} \) . The action of \( D_{4} \) on \( S_{3}^{4} \) is simply a reindexing. So \( G \) is isomorphic to the wreath product (p. 172, [8]) \( D_{4}≀S_{3}^{4} \) . It is of order \( 8×6^{4}=10368 \) . The two features, space and group, are well presented in this model: the cube dance is a graph that encodes musical information, and it has a 10368-fold symmetry.

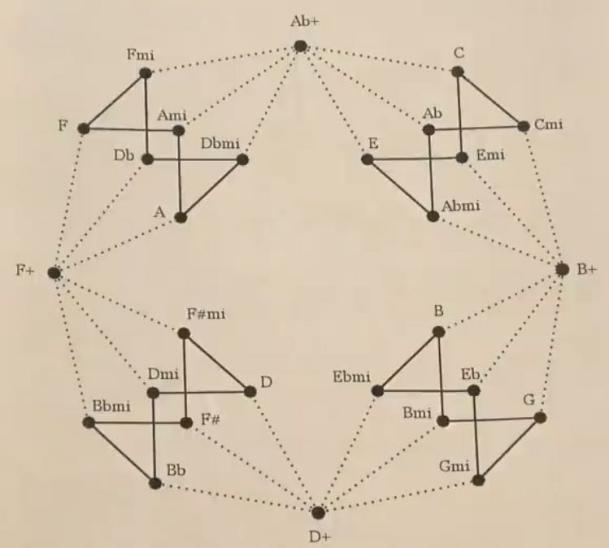
Figure 7. Jack Douthett’s cube dance.

3.3 Fano plane and octonions

The complex numbers form a number system \( C \) that extends the real numbers \( R \) . This extension is achieved by adding an imaginary unit \( i \) to \( R \) , subject to the equation \( i^{2}=-1 \) . It follows that one can add, subtract, multiply and divide numbers of the form \( a+bi \) ( \( a,b∈R \) ) under the usual laws.

The next step to extend \( C \) in a self-consistent way leads to the quaternions \( H \) . Those are numbers of the form \( a+bi+cj+dk \) ( \( a,b,c,d∈R \) ) where \( i,j,k \) are three imaginary units, i.e. \( i^{2}=j^{2}=k^{2}=-1 \) . In order to multiply and divide the quaternions, the relations among \( i,j,k \) need to be specified. Consider an oriented equilateral triangle labelled at vertices by \( i,j,k \) . The relations are implied in this graph:

\( ij=k, jk=i, ki=j, ji=-k, kj=-i, ik=-j. \)

Note that the multiplication does not satisfy the commutative law. We say that the quaternions form a non-commutative normed division algebra over \( R \) .

The next extension of the quaternions is the octonions \( O \) . We have now 7 imaginary units \( e_{i} \) ( \( e_{i}^{2}=-1 \) ), \( 1≤i≤7 \) . The relations are encoded in the following graph, called the Fano plane:

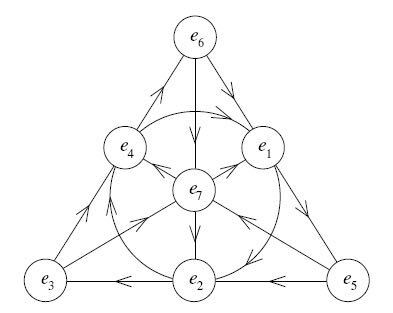
Figure 8. Taken from , week 214.

Each arrow \( e_{i}→e_{j} \) represents a relation \( e_{i}e_{j}=-e_{j}e_{i}=e_{k} \) where \( e_{k} \) is the third vertex on \( e_{i}→e_{j} \) . Together these give the rules on the operations of the octonions \( a+be_{1}+⋯+he_{7} \) ( \( a,b,⋯,h∈R \) ). Now the multiplication is not even associative (e.g. \( e_{1}(e_{2}e_{3})=-(e_{1}e_{2})e_{3}=e_{6} \) ). As a normed division algebra over \( R \) , \( O \) is non commutative and non associative. We can not extend it further, by Hurwitz’s theorem.

Combinatorially, the above figure 8 can be viewed as a structure on a 7-element set. There are its 3-element subsets (called blocks) determined by the arrows. And any 2 elements uniquely determine a block. This is known as the Steiner system \( S(2,3,7) \) . The labeling in the figure is up to automorphism uniquely characterized by the property that, on each block, the 6 differences among the subscripts range over \( 1,2,⋯,6 \) mod 7.

In the view of projective geometry, the figure is the projective plane over the finite field \( F_{2} \) . We can view \( {e_{2},e_{3},e_{4},e_{7}} \) as the affine plane \( F_{2}^{2} \) , then \( e_{1},e_{5},e_{6} \) form the line at infinity. An automorphism is just a projective transformation. It is easy to see that the group of affine transformations on \( F_{2}^{2} \) is \( S_{4} \) , of order 24. To pin down a projective transformation, we need to know which one of the 7 lines the \( ∞ \) line is sent to, then we need an affine transformation. We thus deduce that the group of projective transformations has \( 7×24=168 \) elements. As a matrix group, it is known as \( PGL(3,F_{2})=GL(3,F_{2})=SL(3,F_{2}) \) .

Some music theorists have been trying to relate the octonions to music, by identifying \( e_{1} \) to \( e_{7} \) with the notes C to B in a diatonic scale. Then each line / block represents a triad chord, and we have this 168-fold symmetry in music to be explored. Unfortunately, the triads here are all transpositions of \( {C,D,F} \) , which are not so commonly used in composition.

A similar but much more complicated attempt, as described by the mathematician and musician Noam Elkies in [2], week 234, was trying to label the Steiner system \( S(5,6,12) \) in a musical way. The chromatic scale is the 12-element set, a block represents a 6-note chord, and any 5 notes are contained in a unique chord. Such a system has \( M_{12} \) of order 95040 as the automorphism group. Under certain conditions, Elkies constructed these 6-note chords, and indicated how to write common tone progressions based on their relations. In our upcoming works, we will also take the musical interpretation of the model into account.

3.4 Platonic solids

We describe a tuning system called hexany invented by the music theorist Erv Wilson, in relation to the platonic solids. Recall that to define a way of tuning, we need to find simple integer ratios. While Pythagoras used 3:2 as the generator, Wilson would start with any 4 randomly picked integers, that he called seeds.

Consider for example 2,3,5,7. Mark the numbers at the vertices of a regular tetrahedron. Then at each edge, mark the product of the two numbers at its endpoints. We have thus 6,10,14,15,21,35 on the edges, which we interpret as frequency ratios. By shifting them into the same octave, we get 6 notes 6,14,15,35,10,21, which we are going to use as a scale. In term of consonancy, this sounds not bad since lots of common factors are in it.

Now we can take out the seeds and consider the 6-note scale marked on the midpoints of edges, which are, vertices of a regular octahedron. On each face of the octahedron there are three notes, which we are going to use as the chords in the scale. Note that each edge of the octahedron connects two numbers with common factor. Having the 6 notes and 8 chords at disposal, we can compose and derive a theory of functional harmony as usual. These give a lot of possibilities, all we need is just 4 random seeds.

The octahedron is dual to the cube, so they have the same symmetries. It is well known that the rotational symmetry group of cube is isomorphic to \( S_{4} \) , by the fully faithful action on the 4 diagonals. And the full symmetry group is the product of \( S_{4} \) with the cyclic group of order 2 generated by the antipodal map. So there is this 48-fold cubic symmetry in the hexany music.

Remark. In general, one can take \( m \) seeds, and multiply each \( n \) of them, then obtain the so-called \( (n,m) \) -combination product set. The case (2,4) is the most common, for it has a nice graphic presentation.

Besides tetrahedron, cube and octahedron, there are two more platonic solids: the dodecahedron and icosahedron, which are dual to each other. Their rotational symmetry group is the smallest non abelian simple group \( A_{5}≅PSL(2,F_{5}) \) , of order 60. The full group is the product of it with \( Z/2 \) generated by the antipodal map, of order 120. Inspired by the fact that an icosahedron has 12 vertices, we can ask for a meaningful way of labeling it by the chromatic scale, hence realizing the group as a symmetry in music. In addition, we want this model to reflect a sense of closeness among the 12 notes. To this end, we pose two natural requirements:

• The perfect fifth is the most consonant interval. We want any two notes that differ by a perfect fifth to be as close as possible, i.e. to be adjacent.

• The tritone is the most dissonant interval. We want any two notes that differ by a tritone to be as far as possible, i.e. to be antipodal.

Definition 3.1. A labeling of the icosahedron by \( Z/12 \) is said to be admissible if it satisfies the above two requirements.

To state the admissible condition more concretely, consider the sequence \( a_{i}=7i \) mod 12 in \( Z/12 \) , \( i=1,2,⋯,12 \) . The first requirement states that \( a_{1},a_{2},⋯,a_{12} \) form a Hamiltonian circuit on the icosahedron. The second one states that \( a_{i} \) and \( a_{i+6} \) are antipodal. These restrict the possible labelings to just a few cases (up to automorphism). One of them (figure 9) is

Figure 9. An admissible icosahedron model.

Among the 30 edges (i.e. intervals), 12 are the perfect 5th / perfect 4th, 6 are the major 2nd / minor 7th (they are whole tone transpositions of C-D), 6 are the minor 3rd / major 6th (they are whole tone transpositions of A-C), 6 are the major 3rd / minor 6th (they are whole tone transpositions of G-B).

This is a toy model. Nevertheless, it shows all the important features and principles that we are going to stick to in the next section for the more complicated model.

4 On Klein’s quartic

4.1 Maths background

Historically, Klein discovered his quartic curve as the modular curve of level 7. Specifically, consider the modular group \( PSL(2,Z) \) acting on the upper half plane \( H \) . Define the congruence subgroups \( Γ(n) \) to be the kernel of the natural homomorphisms \( PSL(2,Z)→PSL(2,Z/n) \) , \( n∈N^{*} \) . The Klein quartic curve, denoted by \( K \) , is the compactified quotient space \( H/Γ(7) \) , endowed with the conformal structure inherited from \( H \) . It follows that the orientation-preserving isometry group of the curve Aut \( (K) \) is \( Γ(1)/Γ(7)≅PSL(2,7) \) .

Here, we take another approach following the exposition in [9] to construct \( K \) . The advantage is that meanwhile we obtain the platonic tessellation. Consider below 14 hyperbolic equilateral \( \frac{π}{7} \) -triangles that form a regular tetradecagon:

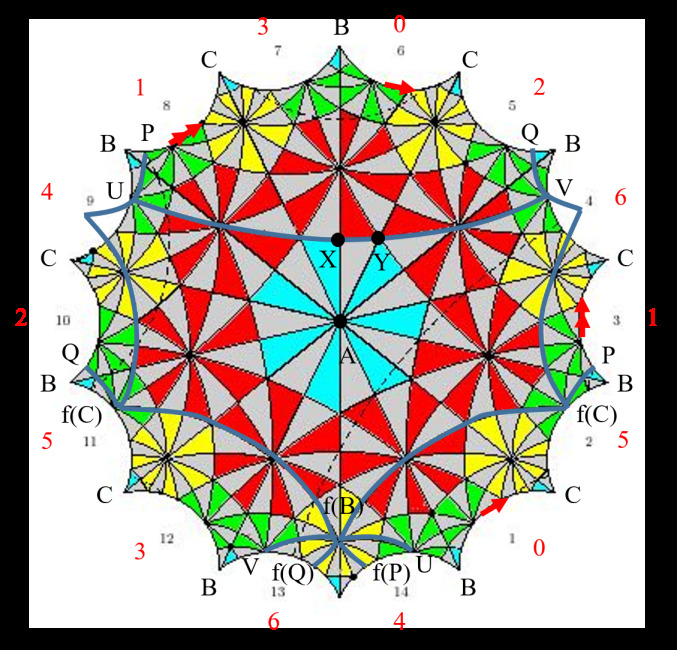
Figure 10. Taken from [2], week 234.

Consider the following gluing process: for each \( 0≤n≤6 \) , identify the edges \( 2n+1 \) and \( 2n+6 \) (mod 14) as indicated by the red numbers and arrows in the figure 10. In this way, we obtain a closed surface. The directions of arrows ensure that the surface is orientable. Note that the gluing collapses 14 edges into 7, and 14 vertices into 2 (i.e. B and C). Hence the surface is a 2-complex with 2 vertices, 7 edges and 1 face. It is hard to visualize but, from computing the Euler number \( 2-7+1=-4 \) , we deduce that the surface is a 3-holed torus.

A crucial fact is that the regular tetradecagon has interior angle \( \frac{2π}{7} \) . This gives the surface a conformal structure. Precisely, using this tetradecagon we produce a hyperbolic tessellation of Schlafli symbol \( {14,7} \) (meaning that at each vertex 7 regular 14-gons meet). This tessellation gives us a universal cover from the hyperbolic disk model \( H \) to the surface. The group of Deck transformations is a cocompact Fuchsian group, denoted by \( G \) . It follows that the surface is \( H/G \) , which is our construction of the Riemann surface \( K \) . In fact, \( G \) is generated by 7 hyperbolic dilations that realize the gluing process, and Aut \( (K)=N(G)/G \) where \( N(G) \) is the normalizer of \( G \) in \( PSL(2,R) \) , the orientation-preserving isometry group of \( H \) .

To study Aut \( (K) \) , we break the tetradecagon into smaller pieces of \( (\frac{π}{2},\frac{π}{3},\frac{π}{7}) \) -triangles. As shown in the figure 10, the A, X, Y are the vertices of a triangle. Fourteen such triangles form a regular heptagon of interior angle \( \frac{2π}{3} \) . Such heptagons then form the hyperbolic tessellation \( {7,3} \) . We can count that \( K \) is made of 24 heptagons, hence \( 24×14=336 \) triangles. Alternatively, by the Gauss-Bonnet theorem a genus 3 surface has hyperbolic area \( 8π \) , and a \( (\frac{π}{2},\frac{π}{3},\frac{π}{7}) \) -triangle has area \( π-\frac{π}{2}-\frac{π}{3}-\frac{π}{7}=\frac{π}{42} \) . It follows that there are \( 8×42=336 \) triangles. This tessellation by heptagons has 24 faces, 84 edges and 56 vertices. We claim that it is regular. First, see [10], section 5.3 for the following result:

Proposition 4.1. The orientation-preserving symmetry group \( G^{ \prime } \) of the tessellation \( {7,3} \) is the (2,3,7)-Dyck’s group

\( G^{ \prime }=⟨x,y|x^{2},y^{3},(xy)^{7}⟩ \)

where \( x \) is the rotation at X by \( π \) , and \( y \) is the rotation at Y by \( \frac{2π}{3} \) such that \( xy \) is a rotation at A by \( \frac{2π}{7} \) . The full symmetry group is generated by the reflections along AX, XY and YA.

Proposition 4.2. \( G^{ \prime }=N(G) \) .

Proof: We first show that \( G^{ \prime }⊂N(G) \) . Clearly the rotation at A is in \( N(G) \) , for it preserves the gluing rule hence defines an automorphism of \( K \) . Then it suffices to prove that \( x∈N(G) \) . Note that \( x \) is the composition of the reflection along AX, and the reflection along XY (denoted by \( f \) ). The former causes no problem since it preserves the gluing. For \( f \) , there are many ways to argue. It should be clear if we can see the figure expanded a bit more. Alternatively, it is feasible though tedious to check that the conjugations of the 7 dilations by \( f \) are again in \( G \) . Our way is to show that \( f \) sends the tetradecagon to another fundamental domain. For this, we divide the tetradecagon by the blue lines in the figure. The part above UV is easy to trace, except the two triangles BPU and BQV are sent by \( f \) to the two triangles at the bottom. The part near the edge 3 is interchanged with the part near the edge 10, expect the two triangles BP \( f(C) \) and BQ \( f(C) \) are sent to the bottom. The remaining two parts, near the edge 1 and 12, are preserved. Together we have the whole tetradecagon. We conclude that \( x∈N(G) \) .

Now we have \( G^{ \prime }/G⊂Aut(K) \) . A fundamental domain of \( G^{ \prime } \) is made of 2 small triangles, hence \( |G^{ \prime }/G|=336/2=168 \) . But by Hurwitz’s automorphism theorem, as a genus 3 surface, \( |Aut(K)| \) can not exceed 168 (essentially it is because the minimal area of a \( (\frac{π}{2},\frac{π}{p},\frac{π}{q}) \) -triangle is \( \frac{π}{42} \) ). It follows that \( G^{ \prime }=N(G) \) , and \( K \) is a Hurwitz surface.

Consequently, the tessellation is regular. Its dual is visualized in figure 3. There we have an equation. Though it has nothing to do with the musical model, let us digress to derive the equation, and realize \( K \) as an algebraic curve.

Proposition 4.3. There is a 7-sheeted branched cover \( z \) from \( K \) to the Riemann sphere \( P^{1}(C) \) , branched at \( ∞=z(A) \) , \( 0=z(B) \) and \( -1=z(C) \) , such that the indices at A, B, C are all 7. There is a 3-sheeted branched cover \( w \) from \( K \) to \( P^{1}(C) \) , branched at \( ∞=w(A) \) and \( 0=w(B)=w(C) \) , such that the indices at A, B, C are 3,2,1 respectively. Moreover, \( (w,z) \) distinguishes points.

Proof: We construct \( z \) and \( w \) . Consider \( K/C_{7} \) , the quotient by the 7-fold rotation \( xy \) at A. It is easy to find a fundamental domain, and observe that \( K/C_{7}≅S^{2} \) . Alternatively, we can prove this by computing the Euler number \( e(K/C_{7}) \) . Suppose that \( xy \) has \( n \) fixed points. Take a \( C_{7} \) -invariant triangulation of \( K \) with \( V \) vertices, \( E \) edges and \( F \) faces, such that all the fixed points are vertices. Then it induces a triangulation on the quotient, with \( n+\frac{V-n}{7} \) vertices, \( \frac{E}{7} \) edges and \( \frac{F}{7} \) faces. It follows that

\( e(K/C_{7})=\frac{6n}{7}+\frac{V-E+F}{7}=\frac{6n-4}{7} \gt 0. \)

We must have \( e(K/C_{7})=2 \) (so it is a sphere) and \( n=3 \) . Indeed, \( xy \) is also the rotation at B by \( \frac{4π}{7} \) , as well as the rotation at C by \( \frac{8π}{7} \) . So the other two fixed points are B and C.

Let \( z:K→K/C_{7} \) be the projection, and identify \( K/C_{7} \) with \( P^{1}(C) \) so that \( z \) is a meromorphic function with \( ∞=z(A) \) , \( 0=z(B) \) and \( -1=z(C) \) . Then \( z \) is a 7-sheeted cover, except at A, B, C it is 1-1.

Next it is natural to consider \( K/C_{3} \) , the quotient by \( y \) . By the same Euler number argument, we have

\( e(K/C_{3})=\frac{2n-4}{3} \gt -2 \)

where \( n \) is the number of fixed points of \( y \) . Since the tessellation is regular, we must have \( n∣56 \) , the number of vertices. We deduce that \( n=2 \) , and \( K/C_{3} \) is a torus. We can not use it to construct \( w \) . Similarly, \( K/C_{2} \) , the quotient by \( x \) , is also a torus. And \( x \) has 4 fixed points.

The construction of \( w \) is via a careful specification on the images of the 14 equilateral triangles. We map A to \( ∞ \) , B and C to 0, and all the triangles meromorphically to some spherical lunes of angle \( \frac{3π}{7} \) . For the triangle 1, let the image of the edge 1 be a slit that has angle \( \frac{π}{7} \) to the image of AC. Reflect the image of triangle 1 to obtain that of triangle 2, etc. Locally at 0 if we let the arg of the image of AB in triangle 1 to be 0, then the 14 edges have arg

\( \frac{2π}{7},\frac{4π}{7},\frac{8π}{7},\frac{10π}{7},\frac{14π}{7},\frac{16π}{7},⋯ \)

from 1-14. We see that the gluing is preserved: the edge 1 coincides with the edge 6, etc. The upshot is that \( w \) is well-defined, and is 3-1 except at A, B, C (the slits need additional check). The index of A is clearly 3. At B (resp. C), each \( \frac{π}{7} \) angle is mapped to a \( \frac{2π}{7} \) (resp. \( \frac{π}{7} \) ) angle, hence the index is 2 (resp. 1). It is straightforward to check that any two points that differ by a 7-fold rotation can not have the same \( w \) value, so \( (w,z) \) distinguishes points.

Remark. In fact, if we spot that the order 2 and order 3 rotations come from two obvious tetrahedron rotations in figure 3, we see easily that they have 4 and 2 fixed points, and that the quotients are both a torus.

Corollary 4.4. The function \( \frac{w^{7}}{z^{2}(z+1)} \) is constant on \( K \) . Up to a scaling, assume it to be -1. Then \( K \) is biholomorphic to the projective variety defined by

\( z^{2}+z^{3}+w^{7}=0. \)

Proof: The function has singularities A, B, C. The numerator and denominator have the same order of zero or pole everywhere, so they are removable singularities. By Liouville’s theorem, the function is constant.

The equation we want to derive is obtained by a substitution \( (x,y)=(\frac{z}{w^{2}},\frac{z}{w^{3}}) \) (the inverse is \( (w,z)=(\frac{x}{y},\frac{x^{3}}{y^{2}}) \) ), hence \( x^{3}y+y^{3}+x=0 \) .

Lastly, we explain the relation to Klein’s construction \( K=\overline{H/Γ(7)} \) , and proposition 1.3. There are exactly 24 punctures on \( H/Γ(7) \) , corresponding to the centers of heptagons. We have a conformal bijection \( g \) from \( K \) minus 24 centers to \( H/Γ(7) \) , that maps a fundamental domain of \( G^{ \prime } \) (i.e. a \( (\frac{π}{3},\frac{π}{3},\frac{2π}{7}) \) -triangle) to one of \( Γ(1) \) (i.e. a \( (\frac{π}{3},\frac{π}{3},0) \) -triangle). By setting \( g(X)=i \) and \( g(Y)=e^{\frac{2πi}{3}} \) , the two rotations at X and Y become the usual generators \( z↦-\frac{1}{z} \) and \( z↦-\frac{1}{z+1} \) of \( Γ(1) \) , which we still denote by \( x \) and \( y \) . After mod 7, \( xy:z↦z+1 \) becomes an order 7 element. Another not so obvious relation is that the commutator \( [x,y] \) has order 4, which can be checked either using the previous figure 10 or using the matrix form. Together we have

\( Aut(K)≅PSL(2,7)=⟨x,y|x^{2},y^{3},(xy)^{7},[x,y]^{4}⟩. \)

Since \( x \) has 4 fixed points, its conjugacy class has \( 84/4=21 \) elements. At the 2 fixed points of \( y \) the rotation angles are \( \frac{2π}{3} \) and \( \frac{4π}{3} \) , so the conjugacy class of \( y \) has \( (56×2)/2=56 \) elements. The rotation \( xy \) has 3 fixed points of angles \( \frac{2π}{7} \) , \( \frac{4π}{7} \) and \( \frac{8π}{7} \) , hence \( (xy)^{-1} \) has rotation angles \( \frac{6π}{7} \) , \( \frac{10π}{7} \) and \( \frac{12π}{7} \) . They form 2 different conjugacy classes of order 7, both of size \( (24×3)/3=24 \) . It remains only one non trivial conjugacy class (see [11], section 27), of size 42. Hence \( [x,y] \) must be a representative of it. This group, and the automorphism group \( PSL(3,2) \) of Fano plane, are both the simple group of order 168. See p.281, [8] for this fact, or see [2], week 215 for a fancy graphic explanation.

4.2 The new model

Finally, we describe our model by a labeling in figure 3. We need a convenient combinatorial characterization of the figure. Clearly it has the shape of a regular tetrahedron. At each vertex (labelled by 0,1,2,3) there is a triangular prism, of 6 vertices.

Definition 4.5. The following labeling (figure 11), with a cyclic order on the two triangles, is called a chromatic prism.

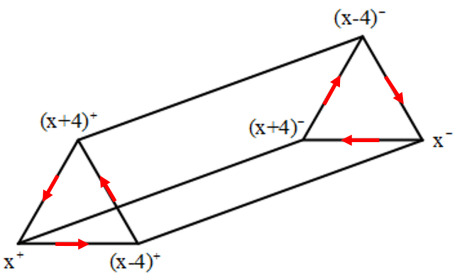
Figure 11. The 4 chromatic prisms, labelled by \( x=0,1,2,3 \) .

Note that the 6 edges of triangles all represent a chromatic mediant progression, while the 3 vertical edges are L transformations (i.e. mediant progression). A chromatic prism uses exactly the 6 chords from a cube of the cube dance.

We define a coding system \( [xy]^{±} \) for the 24 vertices, where \( {x,y} \) is a 2-element subset of \( {0,1,2,3} \) . The \( x \) means that the vertex is in the prism \( x \) . The + or - means that it is in the outer or inner triangle. The \( y \) refers to the prism to which it has no edges (i.e. in the figure 3 the farthest prism from it). The tetrahedron edges represent a distorted cuboid with 4 extra diagonals on the sides. This is encoded as some relations among \( [ac]^{±},[ad]^{±},[bc]^{±},[bd]^{±} \) where \( a,b,c,d \) is any permutation of 0,1,2,3: if the cyclic order in the prism \( a \) states that \( c→d \) , then \( [ac]^{±} \) has two edges to \( [bd]^{+} \) and \( [bd]^{-} \) ; otherwise \( [ac]^{±} \) has two edges to \( [bc]^{∓} \) and \( [bd]^{∓} \) . In this way, we have encoded the whole graph.

Now we need to put specific conditions, for two chords to be allowed to have an edge between them. Let \( d≤6 \) be the difference between their roots in semitones.

• \( d=0 \) , allowed. It is just the P transformation.

• \( d=1,2 \) , allowed. It is the half step or whole step progression.

• \( d=3 \) , there are 4 cases. One is the R transformation, two are chromatic mediants, the remaining one, that we do not allow, is \( x^{+} \) and \( (x+3)^{-} \) .

• \( d=4 \) , there are 4 cases. One is the L transformation, two are chromatic mediants, the remaining one, that we do not allow, is \( x^{-} \) and \( (x+4)^{+} \) .

• \( d=5 \) , allowed. They are subdominant-to-tonic progressions, though iv - I and iv - i have much weaker function than IV - I and IV - i, and are less common.*

• \( d=6 \) , allowed, but we try to avoid. In the tritone case, the progressions sound very dissonant and are only used for special purpose. They do show up in the piece that we are going to analyze, though.

Definition 4.6. A labeling of the 24 triads on the 24 vertices of the triangulation of \( K \) is said to be admissible, if no edges are labelled by \( x^{+},(x+3)^{-} \) or \( x^{-},(x+4)^{+} \) .

It is a mild condition. We have quite a few admissible labelings using the chromatic prisms. Among them, the following one (figure 12) definitely appeals to us the most, and should be picked as the best candidate (we only draw the outer triangles):

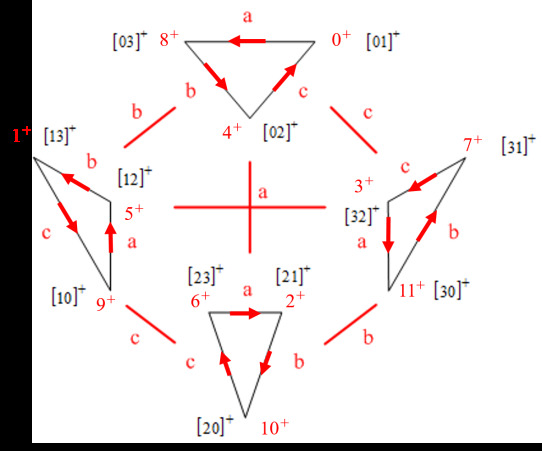
Figure 12. Our favorite admissible labeling.

Here the letters a, b, c imply the cyclic orders, as well as the 6 cuboids. Note that the emanating vertices of a are 0,9,6,3 respectively (however, the transposition \( x↦x-3 \) is not in Aut \( (K) \) ). Up to transposition, the 2 cuboids labelled by a are both of the form as below.

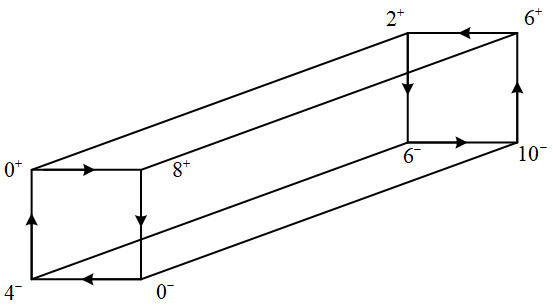
Figure 13. The cuboid a.

The figure 13 means that \( 0^{+} \) is connected to \( 6^{+} \) and \( 10^{-} \) , \( 8^{+} \) is connected to \( 10^{-} \) and \( 6^{-} \) , etc. The transposition forms of b and c are similarly shown below (figure 14 and figure 15):

Figure 14.The cuboid b.

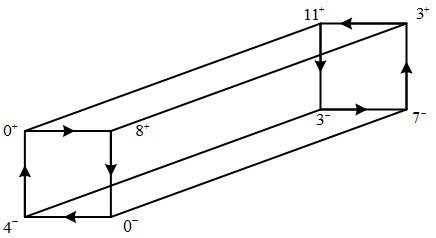
Figure 15.The cuboid c.

A close inspection of these figures verifies that the labeling is admissible. In fact, the chromatic prisms ensure that \( x^{-} \) is never connected to \( (x+4)^{+} \) . The other forbidden pair can only appear in the cuboid b or c. We verify that \( (9^{+},0^{-}) \) in b and \( (0^{+},3^{-}) \) in c are not connected. We shall call this model Klein’s dance.

Among the 84 edges, there are exactly 12 half step progressions, 12 whole step progressions, 12 dominant-to-tonic progressions and 12 L transformations. Only 4 edges are tritone progressions, while 32 edges are chromatic mediant progressions, which is a lot. This is because the 4 chromatic prisms already take up 24 of them. Nevertheless, we like this progression. It is fair to say that our model shows a lot of preference to the chromatic mediant. Below (taken from [2], week 214) we have our model drawn on the hyperbolic plane (figure 16). The gluing rule is spotted in the figure.

We can study the action of the order 168 group Aut \( (K) \) on the triads. For example, the involution that interchanges C and F \( ^{♯} \) is the tritone transposition musically. As an involution, recall that it has 4 fixed point. They are precisely on the 4 tritone edges.

Despite the apparent symmetry and beauty in Klein’s dance, there are some flaws. The major one is that, we have no other transposition except the tritone one (Aut \( (K) \) contains no order 6 or order 12 elements), which results in an asymmetry of notes, hence we can not express the edges coherently as 7 basic transformations. Moreover, we are missing the P and R transformations. We had considered to set the vertical edges in the prisms to be P transformations instead of L, but we failed to find an admissible model. Nevertheless, we have an abundance of types of progressions in this framework, as opposed to the Tonnetz model. This advantage will support harmonic analyses of some rather complex pieces, as we will soon see.

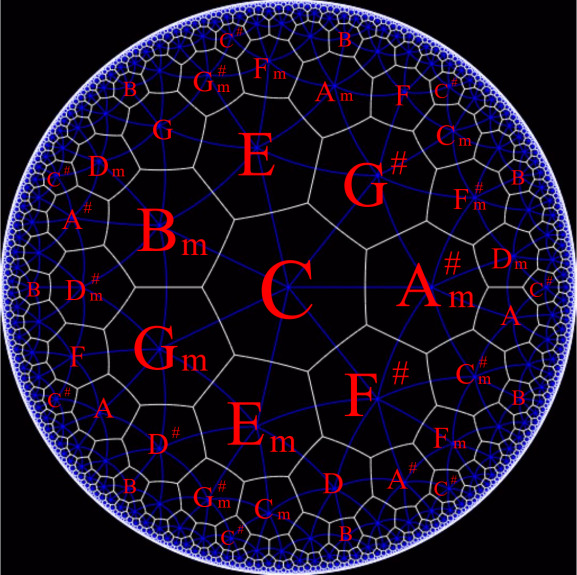
Figure 16. Another view of our model.

4.3 Variations and application

Klein’s dance is our favorite model, but of course is not the unique admissible model. Some other admissible models can be obtained as slight variations of it. We discuss what are they, and explain for what musical purposes we choose such variations.

11 An obvious variation is via musical transpositions and inversions. It follows directly from the definition that, \( T_{n} \) or \( I_{n} \) (which changes the tonality) of an admissible labeling is again admissible. The operations that produce an equivalent labeling (e.g. \( T_{6} \) as just mentioned) form a subgroup \( H \) of \( D_{12} \) . We claim that \( H={e,T_{6},I_{1},I_{7}}≅(Z/2)^{2} \) . Note that the \( D_{12} \) -action preserves the type of progressions (half step, whole step, etc.), in particular if \( x∈H \) , it permutes the 4 tritone edges \( (0^{±},6^{±}) \) , \( (3^{±},9^{±}) \) . This leaves just a few cases to check and the claim follows. We conclude that the \( D_{12} \) -action gives \( 24/4=6 \) variations (including the trivial one). This enables us to transpose or invert a piece, then do the analysis on Klein’s dance.

12 We observe that, all the half / whole step progressions and dominant-to-tonic progressions change the tonality, which does not quite fit with the reality. We have an easy way to fix this: take any chromatic prism, flip all three L edges (so that the outer and inner triangles are interchanged). This variation is admissible by a quick inspection of the cuboids b and c. However, flipping at the same time two prisms connected by b or c is not admissible. We can do this only when they are connected by a. It is clear that the flipping operations commute with the \( D_{12} \) -action. Taking the \( T_{6} \) -invariance into account, we have \( 2+2=4 \) variations (not including the trivial one) in this way.

13 We still want to replace (at least some of) the L edges by P edges, because we think the parallel progression is an important one. To do this admissibly, we modify a chromatic prism under the conditions that

• Inside the prism, no \( x^{-} \) with \( (x+4)^{+} \) is connected.

• Some vertical edges are P transformations.

• No matter how the other 3 prisms are flipped, no \( x^{+} \) with \( (x+3)^{-} \) is connected.

By a tedious enumeration, for the prism 0, these conditions restrict to 5 cases below. The other 3 prisms similarly have 6 variations (including the trivial one) by transposition (figure 17).

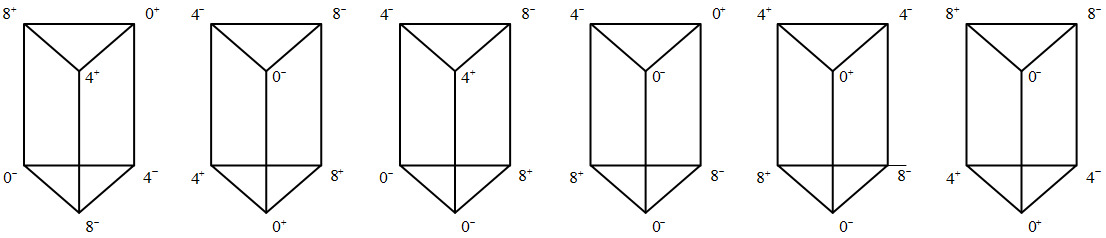
Figure 17.The original prism 0, with 5 variations.

The hybrids of these 3 types of variation yield lots of admissible labelings, though some of them might be equivalent. For example, take two prisms connected by b or c. For one, choose one of the six variations above. For the other, decide independently whether flip it or not. Then globally apply a \( D_{12} \) -operation. The labelings obtained from this procedure are all admissible and distinct from each other. So we have at least \( 6×2×6=72 \) non equivalent admissible variations, which should cover lots of musical contexts.

As an example of application, we analyze the first 16 measures of the celebrated theme music The Imperial March by John Williams. This is a classical style piece, with high harmonic complexity. It is in the key of G minor, and the chord progression (modulo some repetitions) is

\( G_{m} E_{m}^{♭} / G_{m} C_{m}^{♯} E_{m}^{♭} / G_{m} E^{♭} / G_{m} C_{m}^{♯} E_{m}^{♭} / G_{m} C_{m} G_{m}. \)

The iconic leitmotif just moves back and forth between the tonic chord and the chromatic mediant chord \( E_{m}^{♭} \) . As a new phrase comes in, John Williams inserts a tritone progression \( G_{m}-C_{m}^{♯} \) , to add even more tension. Then we have a very brief major chord VI, which is the only major chord used in the entire piece. The paragraph ends with a plagal cadence iv - i.

This harmony line contains various types of progression. It is well presented in one of the variations of Klein’s dance. Namely, choose the 5th variation of the prism 0, and flip the prism 3. As seen below, the progression traces a loop on this variation (figure 18).

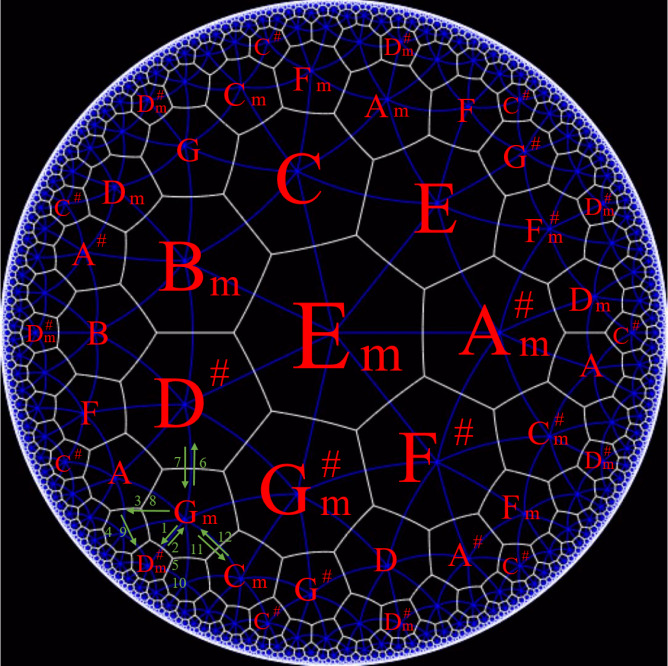
Figure 18.The Imperial March chord progression.

The key vision is that, can we reverse this process, and use it as inspirations for our composition? After all, we have so many types of progression and so many variations with different flavor at disposal. Could this theory be used in AI-generated music? We see the potential.

5 Conclusion

Neo-Riemannian analysis is a framework of doing musical analysis using graphs and topological spaces. Specifically, a graphic representation of the 24 triad chords on a torus encodes some basic chord transformations. In our work, we mimic this theory and invent a musical model represented on the Klein’s quratic curve. The Klein’s quartic curve is an algebraic variety that can be decomposed into 24 regular heptagons in the hyperbolic plane, 84 edges and 56 vertices. We put exactly one traid chord in each regular heptagons, in a way that the adjacent faces encodes musically meaningful chord progessions. The Klein’s quartic curve has the automorphism group of order 168, we use this 168-fold symmetry to construct more variations of our model proposed, and show the potential of using these models to do harmony analysis.