1. Introduction

The existence of dark matter was first proposed to explain the phenomenon of galaxy rotation curves. According to the theory of gravity, the rotation speed of galaxies should decrease as one moves towards the outskirts of the galaxy. However, the observed data show that an additional mass component, which is a hypothetical substance called dark matter, needs to be introduced so that the rotation speed can remain relatively constant. So, whether dark matter, this imagined substance, truly exists becomes a question. In this paper, the author delves into discussions on dark matter from various perspectives, such as rotation curves, because significant discrepancies are found between the calculated mass and some observed phenomena related to mass in the universe. Dark matter constitutes the majority of the material in the universe. By studying the distribution and properties of dark matter, this paper can better understand the formation of the universe’s structure, including the formation of galaxies and galaxy clusters. The existence of dark matter has significant implications for measuring and inferring cosmological parameters. It allows for a more accurate determination of parameters such as the density of matter and dark energy in the universe. Research into techniques and methods related to dark matter, such as astronomical observation techniques, often leads to technological innovation and advancement.

2. Background and basic observational research on dark matter

Measuring the mass of distant celestial bodies is a challenging task. Based on the principles of Newton’s law of universal gravitation and Newton’s second law, the mass of celestial bodies can be inferred through the observation of their motion (see Fig. 1). As early as 1884, William Thomson (also known as Lord Kelvin) estimated the mass of the Milky Way galaxy’s center based on the speed of star movement, but it is found that this estimated mass exceeded what visible stars could provide. Consequently, he proposed a conclusion that many celestial bodies are possibly “dark stars”. Through the method of measuring star motion speeds, Jacobus Kapteyn in 1922 and Jan Oort in 1932 also found “dark matter” in the Milky Way galaxy, with a mass exceeding what visible stars can provide. However, due to limitations in observation technology, the measurements were not precise, leading to some uncertainties.

Figure 1. Orbital velocity of a galaxy.

The most crucial evidence came in 1933. When Swiss astronomer Fritz Zwicky was studying the motion of member galaxies in the Coma Cluster, he found that these galaxies’ velocities were unusually high. This led to a surprising conclusion that the dark matter in the Coma Cluster exceeded the mass of visible member galaxies by hundreds of times, indicating that the majority of its mass was “invisible”.

Figure 2. Galaxy rotation curve.

Rotation curves of galaxies refer to the curves formed by the distribution of the velocities at which celestial bodies rotate around the center of galaxies at different positions. For example, in the solar system, plotting the relationship between the rotational velocity of planets around the Sun and their orbital radii yields the rotation curve of the solar system. According to Newton’s law of universal gravitation and the second law, rotational velocity should decrease inversely proportional to the square root of the radius. Actual measurement results have also accurately verified this relationship (see Fig. 2) [1].

3. The precise proof of dark matter

3.1. Rotation curve of galaxies

As time passed and technology advanced, scientists began to conduct more precise research. The rotation curve of a galaxy is a function curve describing the relationship between the speed of stars or gases orbiting the center of the galaxy and their distance from the center of the galaxy disk. Under reasonable assumptions, measurements of the galaxy’s rotation curve can be used to predict the galaxy’s mass. Considering that the rotational speed of stars is much smaller than the speed of light, that is, in the non-relativistic case, Newton’s laws of motion are generally applicable. If the mass of the galaxy is mainly concentrated in the galaxy’s disk, then according to Newton’s inverse square law, the velocity of stars farther from the galaxy’s disk can be simplified as:

\( v(R)≈\sqrt[]{\frac{{GM_{disk}}}{R}} \) (1)

Here, v represents the speed of the stars, r represents the distance of the stars from the center of the galaxy’s disk, and M represents the mass of the galaxy’s disk. In theory, as the distance increases, the speed of stars should gradually decrease. However, astronomers have measured the rotation curves of some galaxies and obtained a series of flat curves [2].

3.2. Gravitational lens

According to the General Theory of Relativity, the intrinsic connection between matter and four-dimensional spacetime can be described through Einstein’s gravitational field equations:

\( {R_{μν}}-\frac{1}{2}{Rg_{μν}}+{Λg_{μν}}=\frac{8πG}{{c^{4}}}{T_{μν}} \) (2)

Where \( {R_{μν}} \) is the Ricci tensor, \( R \) is the scalar curvature, \( {g_{μν}} \) is the metric tensor of four-dimensional spacetime, \( {T_{μν}} \) is the energy-momentum tensor, \( G \) is the gravitational constant, and \( c \) is the speed of light.

Figure 3. The observational image of the Bullet Cluster.

General relativity predicts the gravitational lensing effect, wherein space is curved near massive objects such as stars, galaxies, or galaxy clusters. When light from distant sources passes through these regions, the light rays bend as if passing through a lens. Subsequently, multiple images of the light source can be observed through astronomical telescopes. The gravitational lensing effect is an important tool for studying the distribution of dark matter, the structure of dark matter halos, and large-scale structures in the universe, depending on the strength and effects of the gravitational field of the lensing celestial bodies. Fig. 3 is an observational image of the Bullet Cluster. The image represents the result of two galaxy clusters colliding and passing through each other. This image combines observations from X-rays and weak gravitational lensing. The red, yellow, and blue regions represent the distribution of baryonic matter obtained through X-ray observations, while the green contour lines represent the distribution of the total mass of the galaxy clusters obtained through weak gravitational lensing effects. The reason for the non-coincidence of the two regions may be due to electromagnetic interactions between baryonic matter, while the interaction between dark matter and ordinary matter may be comparatively weak, resulting in different velocities when dark matter and ordinary matter traverse through each other in another galaxy cluster. The observational phenomenon of the Bullet Cluster not only indicates the existence of a large amount of dark matter within the galaxy clusters but also suggests that dark matter is primarily non-baryonic [3].

3.3. Distribution of celestial bodies in the universe

The distribution of celestial bodies and the presence of dark matter are closely related. In the universe, observed celestial bodies include stars, galaxies, and galaxy clusters. According to gravitational theory, the distribution and motion of celestial bodies are influenced by gravitational interactions. However, based on the masses of celestial bodies and their gravitational effects, the observed trajectories of celestial bodies deviate from the expected ones, indicating the existence of additional material, namely dark matter. As depicted in Fig. 4, the distribution of galaxies appears filamentous and irregular. This paper uses dark matter to explain this peculiar phenomenon. Based on spectral redshift measurements (left, top) and galaxy distribution obtained from cosmological simulations (right, bottom), the total number of dark matter particles diminishes as dark matter annihilation progresses in scenarios where standard model particles lack sufficient energy to generate dark matter. This decline continues until the annihilation rate of dark matter falls far below the Hubble rate. At this juncture, dark matter decouples from thermal equilibrium, and its co-moving density remains constant, a phenomenon known as the “freeze-out” mechanism.

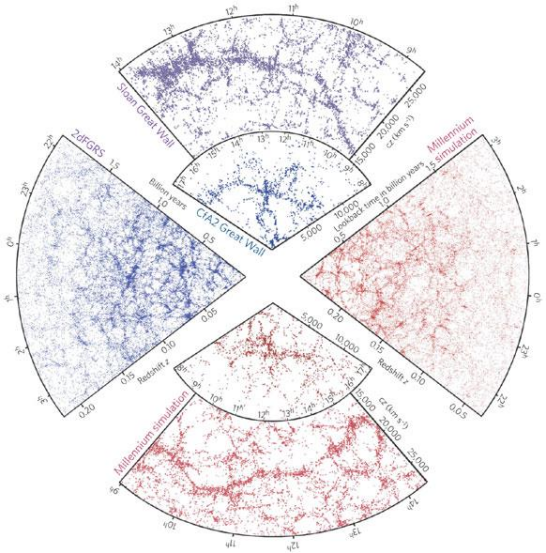
Figure 4. Image of Cosmic Microwave Background Radiation.

Under the freeze-out mechanism, the simplest scenario involves dark matter particles being generated through a 2-2 annihilation process. The evolution of the density of dark matter particles with the expansion of the universe can be described by the Boltzmann equation [4].

3.4. Microwave background radiation

After about 380,000 years following the Big Bang, the temperature of the universe dropped to \( T≈3000 K \) , and photons decoupled from electron-photon plasma. The nearly perfect blackbody radiation produced at this time is a relic of the Big Bang, known as the Cosmic Microwave Background (CMB). With the expansion of the universe, the current temperature of the CMB has decreased to \( T≈2.725 K \) . Anisotropies in the microwave background radiation can be observed on scales smaller than 5: \( δT/T∼{10^{-5}} \) . These anisotropies mainly stem from density fluctuations in the early universe and contain a wealth of cosmological information. The temperature power spectrum, varying with angular scales, can be described using dark energy as a cosmological constant \( Λ \) and specifying six basic parameters ( \( {Ω_{b}}{h^{2}} \) , \( {Ω_{c}}{h^{2}} \) , \( {100θ_{MC}} \) , \( τ \) , \( {n_{s}} \) , \( ln({10^{10}}{A_{s}}) \) ) in the \( ΛCDM \) model. In 2018, the Planck satellite provided the latest CMB temperature angular power spectrum. The abscissa represents the order of the multipole moment, proportional to the reciprocal of the angular resolution, such as 180°. The position and amplitude of the first acoustic peak in the power spectrum include information about the total energy-matter content in the universe and are related to the “flatness” of the universe; the second acoustic peak is related to ordinary matter in the universe; the third acoustic peak is related to dark matter in the universe. Through analysis, the Planck collaboration provided precise contributions of different components to the total energy in the universe (TT, TE, EE+lowE+lensing, 68% limits): \( {Q_{b}}{h^{2}} \) =0.02237±0.00015, \( {Ω_{υ}}{h^{2}} \) =0.1200±0.0012, \( {Q_{a}}/{Ω_{b}}{h^{2}} \) =0.3107±0.0082, where \( {Q_{b}} \) , \( a \) , and \( Λ \) distributions represent the densities of baryonic matter, cold dark matter, and dark energy, respectively.

4. Detection of dark matter

Although multiple pieces of evidence from astronomy and cosmology have already indicated the existence of dark matter, its fundamental properties are still not understood. Further research on the particle level is needed to explore the relevant issues of dark matter. As shown in Fig. 5, based on the different interactions between dark matter particles (DM) and standard model particles (SM), the detection methods of dark matter can be categorized into direct detection, indirect detection, and collider detection. Currently, various dark matter detection experiments worldwide are striving to search for dark matter particles. However, except for a few experiments that have provided ambiguous signals, most experiments have not detected clear signals of dark matter [5].

Figure 5. Dark Matter Particles and Standard Model Particles.

4.1. Direct detection

The feasibility condition for direct detection of dark matter is based on the assumption that there exists weak interactions between dark matter particles and standard model particles. As the Earth moves through the dark matter halo, a large number of dark matter particles pass through the Earth and interact with the nuclei in the detector. Direct detection experiments primarily involve precisely measuring the recoil energy of target nuclei, thereby directly probing dark matter events and studying the properties of dark matter. The detection methods mainly include the direct detection of recoil events and the study of the annual modulation effect of recoil event rates. So far, only a few experiments have reported potential signals of dark matter, but the majority of direct detection experiments have not detected any signals beyond the background noise, only providing upper limits on the scattering cross-section of dark matter with nuclei. Additionally, there are significant discrepancies between different direct detection experiments. Apart from the overlapping regions in the parameter space of mass and cross-section for experiments such as CDMS and CoGeNT, the permitted regions provided by other experiments do not coincide (see Fig. 6).

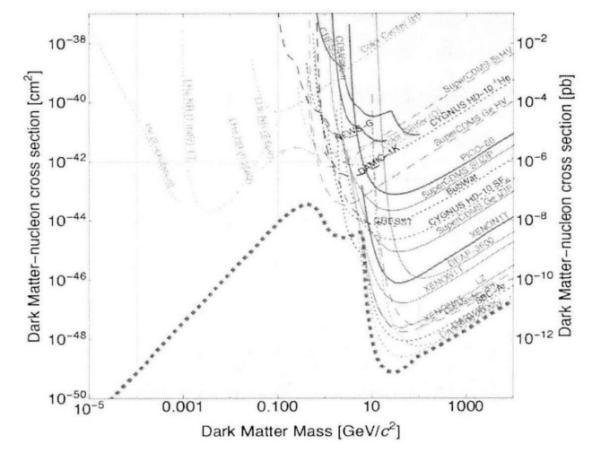
Figure 6. The interaction between dark matter particles and standard model particles.

4.2. Indirect detection

Indirect detection experiments for dark matter primarily rely on ground-based telescopes and space-based detection satellites to observe the particle streams produced during decay processes, including positrons, electrons, antiprotons, photons, neutrinos, and light nuclei. Photons and neutrinos, being electrically neutral, are not influenced by electromagnetic fields in the Milky Way and can therefore preserve spatial information from their source. Charged particles, on the other hand, experience multiple deflections and accelerations due to electromagnetic fields as they move within the Milky Way, and their motion can be approximated using diffusion models. If signals exceeding or deviating from the expected background are detected in astrophysical contexts, they may originate from the annihilation or decay of dark matter. Indirect detection methods for dark matter can be categorized into gamma-ray detection, neutrino detection, and antiparticle (positrons, antiprotons) detection based on the characteristics of the final state particles. As shown in Fig. 7, these phenomena may originate from the annihilation and decay of dark matter [6].

Figure 7. The interaction between dark matter particles and standard model particles.

4.3. Collider detection

Current high-energy colliders can accelerate particles of the standard model to high-energy states, thereby simulating the early stages of the universe, and may produce dark matter particles. According to the current understanding of the properties of dark matter, dark matter particles are invisible near the collision points of colliders. However, information about dark matter particles can be reconstructed by analyzing the lost energy.

An important question in collider detection of dark matter is the need to understand the production process of dark matter. In model-independent scenarios, dark matter signals can be identified from individual events accompanied by lost energy, such as jets, γ, Z, Higgs, and gray events (see Fig. 8). Additionally, new mediator particles may exist in dark sectors, which can decay into dark matter or quarks of the standard model. Collider detection experiments can also explore these new mediator particles, such as dark photons [7].

Figure 8. The collision point.

5. Conclusion

Based on the research on dark matter, this paper gathers sufficient evidence to support its existence. However, the actual observation of dark matter remains elusive. Instead, this paper relies on comparisons between calculated values and observed data. Dark matter is introduced to better explain the discrepancies between these values. One limitation of this paper is the lack of discussion on certain aspects. Currently, some scientists are exploring modifications to gravity, suggesting that force (F) and distance (R) are inversely proportional. When plotted, these modifications exhibit striking similarities to observed velocities. However, their applicability is limited to addressing issues related to rotation curves. In conclusion, this paper believes that future research should focus more on exploring modifications to gravity [8].