1.Introduction

Sea lamprey is one of the existing representatives of gnathless vertebrates [1]. Lampetra japonica, which appeared 360 million years ago, is a migratory marine organism belonging to the class Cyclostomata, Petromyzontiformes, Petromyzontidae, and Lampetra, and is the most primitive jawless vertebrate known to date [2]. In natural ecosystems, most species can have a 1:1 sex ratio at birth, but some species have unequal sex ratios due to changes in adaptive sex ratios. The sea lamprey is a parasite that has a significant impact on the ecosystem, and its sex ratio may be different due to differences in the external environment.The availability of food affects the growth rate of the larvae, and the growth rate of the larvae determines the final sex, which is lower in ecosystems with insufficiene food supply.

Given that the availability of resources described above can alter the sex ratio, this work aims to model and analyze the dependence of the sex ratio on the environment in order to understand the resulting interactions in the ecosystem, which is particularly important for us. To this end, we make the following assumptions:

Hypothesis 1: The population dynamics of sea lamprey is affected by dependent populations, and the changes in the number of dependent populations are directly or indirectly affected by the changes in population dynamics and sex ratio of sea lampreys.

Hypothesis 2: The sex ratio of sea lampreys varies with food availability.

Hypothesis 3: The main food source of sea lamprey is farmed and eaten in nature, and the total amount of food is not affected by extreme weather conditions.

2.Research Methods

2.1.Logistics regression model

The Logistics regression model is a commonly used model to describe population dynamics, in which the rate of change in sex ratio is greatly affected by environmental load, and is suitable for the population growth of lamprey under resource-limited conditions. Logistics regression is a classical statistical model, compared with other statistical models, its prediction effect is better, compared with machine learning models, the modeling process of logistic regression model is relatively simple. In order to explore the influence of ecological environment on the sex of lampreys, a dynamic model of lamprey population, a dynamic model of lamprey population, a dynamic model of lampray eel, and a dependent population model were established, and the kinetic model of Zheng Liwei and Chen Xiaolei (2024) was used to determine [3] the sex ratio, mortality, mortality rate and mortality rate of lamprey population. Rate of change in food sources and dependence on tribulus populations. At the same time, we have taken the following steps with this model:

1. Establish a dynamic model of the light eel population: the model should include factors such as birth rate, mortality rate, rate of change of food source, and dependent population of light eel.

2. Model the dynamics of food sources: The model should take into account the availability and rate of change of food sources.

3. Establish a dependent population model: The model should take into account the interactions of lampreys with other dependent populations.

4. Integrating these three models into a single comprehensive model will allow us to explore how these factors work together to influence the sex ratio of lamprey populations.

5. Collect data: Collect actual data on lamp eel populations, food sources, and dependent populations.

6. Fitting the model: Use the collected data to fit a comprehensive model.

7. Results: Analyze the results of the fitted model to determine how factors such as environmental load affect the sex ratio of the lamprey population.

2.2.Correlation Models

This correlation model is widely used as a mathematical tool for calculating detailed sensitivity data of a system under specific boundary conditions. This method can be used for engineering optimization and other problems to achieve multiple goals under different working conditions. In this paper, the knock-on effect of lamprey and its impact on ecosystem stability were studied.

2.3.Ecological dynamics model

In ecosystems, there are multiple interactions of competition, predation, reciprocal symbiosis, and parasitism among populations, and the construction of mathematical models is the most commonly used tool to study the interactions between species in ecosystems, and many population models have been proposed. The ecosystem dynamics model is a tool that can be used to model the interactions of different species within a natural ecosystem, and the development of ecosystem structure and function. Several important factors must be considered when modeling ecosystem dynamics: ecosystem structure, interspecies interactions, invasive species, biodiversity, and environmental factors. Constructing a complete model of ecosystem dynamics needs to consider the interaction of these aspects. In this paper, this model was selected to analyze the impact of lamprey population on the ecosystem from different aspects.

The ecosystem dynamics model is a tool that can be used to model the interactions of different species within a natural ecosystem, and the development of ecosystem structure and function. Several important factors must be considered when modeling ecosystem dynamics: ecosystem structure, interspecies interactions, invasive species, biodiversity, and environmental factors. Constructing a complete model of ecosystem dynamics needs to consider the interaction of these aspects. In this paper, this model was selected to analyze the impact of lamprey population on the ecosystem from different aspects.

3.Empirical analysis

3.1.Model Preparation

Lampreys grow male or female in the larval stage, and the larval growth rate is affected by the food supply, and its normal sex ratio is affected by the external environment. At the same time, the sex ratio also affects the reproduction rate of the species, and thus the external environment. Therefore, the change of the sex ratio of lamprey is a complex issue, which needs to be considered from multiple aspects, such as birth and death rates (i.e., population dynamics), food sources (i.e., resource use), and dependence on populations (i.e., interactions between organisms) to consider the impact of changes in the sex ratio of groups on larger ecosystems.

For the sex ratio of lampreys affected by environmental factors, the logistic regression model can be used to distinguish lampreys of different sexes, and the difference model can be constructed and the corresponding results can be obtained.

To observe the effect of changes in the sex ratio of lampreys on ecosystem stability, to introduce intermediate hosts as independent populations, and to consider multiple subpopulations of other species as well as environmental conditions in the ecosystem. By modeling the ecological dynamics and incorporating the sex ratio as a variable into the individual equations, we can fully understand the impact of changes in the sex ratio of lamprey populations on ecosystem stability.

Then, a lamp eel population model and a parasite population model were developed, merged and coupled to the whole system, and quantitative studies were made to quantitatively investigate whether changes in the sex ratio of lampreys provided an advantage for parasites.

3.1.1.Kinetic model. To describe the dynamics of lamp eel populations, we use logistics regression models to simulate birth rates, mortality rates, and corresponding dynamics of lamp eel populations based on their dependent populations

Xt: The total number of sea lampreys representing time t

Gt: Represents the total amount of the main food source at time t

Pt: Indicates dependence on lampreys feeding on other populations at time t

|T-t|: indicates the deviation of the lamprey from the appropriate temperature

Rt: Represents the total amount of nutrients available at time t

Suppose the birth rate of the lamprey population: b(|T-t|，Rt，t，St）

Mortality rate of sea lamprey population: d(|T-t|，Rt，t，St）

\( \frac{d{x_{t}}}{dt}=b(|T-t|,{R_{t}}){X_{t}}-d(|T-t|,{R_{t}}){X_{t}} \)

\( b(|T-t|,{R_{t}})={b_{1}}|T-t|+{b_{2}}{R_{t}}d(|T-t|,{R_{t}}=\frac{{d_{1}}}{|T-t|}+\frac{{d_{2}}}{{R_{t}}} \)

3.1.2.Adjoint Models. The adjoint model method is based on the adjoint assimilation method, which has the following advantages compared with the adjoint method of the first control theory. The difference between the gradient of the cost function and the simulation method can be added directly to the power of the adjoint equation. In the adjoint model, we should prepare the following:

1. Lampray population model: a dynamic model that includes factors such as the change of lampill population, the change of sex ratio, the birth rate, and the mortality rate.

2. Parasite population model: describes changes in parasite populations over time, as well as parasite infection and mortality rates.

3. Coupled model: The impact of changes in the sex ratio of lamprey population on the number of parasites was studied by combining the lampill population model with the parasite population model.

4. Relevant parameters and variables: including lampill population growth rate, environmental capacity, sex ratio adjustment rate, stability rate and other parameters, as well as parasite infection rate, mortality rate and other parameters.

5. Data analysis method: used to analyze the results of the model and evaluate the impact of the change of sex ratio of lamprey population on the number of parasites.

The above will help to study the effect of changes in the sex ratio of lamprey populations on the number of parasites.

3.1.3.Ecological dynamics model.

3.1.3.1.Population model of sea lamprey.

\( \frac{dX}{dt}={r_{X}}(1-\frac{X}{k})-{Z_{X}}{M_{X}}-{d_{X}}(1-M) \)

\( \frac{dM}{dt}=a(b-M)-e{M_{X}} \)

In the formula, Xt is the population of Lampgill Eel, Mot is the male sex ratio, r is the growth rate of the lamprey, K is the upper environmental capacity, Z is the male and female mating efficiency, d is the female mortality rate, a is the adjustment rate of the sex ratio, b is the stability ratio, and e is the effect of the number of lampreys on the sex ratio.

3.1.3.2.Parasite population model. Exploring the nutritional relationship between lampreys and their parasites can provide important ecological data for the interpretation of marine ecosystem functions and changes [4]. The parasite and lamprey are in the same ecosystem, and the two species compete to some extent. To demonstrate that changes in the sex ratio of lampreys are dominant for other species in the ecosystem, such as parasites, the following parasite population models were established:

\( \frac{dP \prime }{dt}=f{M_{X}}-gP \prime \)

where P'_(t) represents the parasite population, f represents the probability of lampill infection, and g represents the parasite mortality

3.2.Model building

3.2.1.Models of food source dynamics. Hypothetical lamprey food growth rate: g(Gt,Xt)

Lamprey reduction rate: h(Gt,Xt)

\( \frac{d{G_{t}}}{dt}=g({G_{t}}{,X_{t}}){G_{t}}-h({G_{t}},{X_{t}}){G_{t}} \)

\( g({G_{t}},{X_{t}})={g_{1}}{G_{t}}-{g_{2}}{X_{t}} \)

\( h({G_{t}},{X_{t}})={h_{1}}-{h_{2}}\frac{{x_{t}}}{{G_{t}}} \)

3.2.2.Dependent population model. Predator predation strategies and prey avoidance strategies are important research topics in evolutionary ecology. Predators and prey gain maximum benefit by adjusting their behavior, thereby increasing their population biomass. Foores escape predation through shelters, while predators increase predation through cooperation [5]. Lamprey-dependent populations can be seen as predators in the food chain, which will have an impact on the sex of lampray populations.

Assuming lamprey dependent population birth rate: p(Gt,Xt)

Lamprey-dependent population mortality: q(Gt,Xt)

\( \frac{d{p_{t}}}{dt}=p({G_{t}},{X_{t}}){p_{t}}-q({G_{t}},{X_{t}}){p_{t}} \)

\( p({G_{t}},{X_{t}})={p_{1}}{G_{t}}-{p_{2}}{X_{t}} \)

\( q({G_{t}},{X_{t}})={q_{1}}-{q_{2}}\frac{{X_{t}}}{{G_{t}}} \)

3.2.3.Model of the impact of sex ratio change on ecosystem stability.

3.2.3.1.Impact model on intermediate hosts. In the case of changes in sex ratio, the ecological dynamics model was used to study its impact on ecosystem stability. To do this, we added the intermediate host Wt as an independent population, describing the rate of change that grows naturally and is less affected by lamprey Xt, where m and n represent the rate of change of the intermediate host, respectively.

\( \frac{d{W_{t}}}{dt}=m{W_{t}}-n{X_{t}}{W_{t}} \)

3.2.3.2.Correlation models with the number of subpopulations of other species. Considering that other species Yt may have multiple subpopulations, where Y1, Y2 represent the number of subpopulations of other species, the negative impacts caused by resource competition between different subpopulations are described.

\( \frac{d{Y_{1t}}}{dt}={e_{1}}{Y_{1t}}-{f_{1}}{X_{t}}{Y_{1t}}-{g_{1}}{Y_{1t}}{Y_{2t}} \)

\( \frac{d{Y_{2t}}}{dt}={e_{2}}{Y_{2t}}-{f_{2}}{X_{t}}{Y_{2t}}-{g_{2}}{Y_{1t}}{Y_{2t}} \)

3.2.3.3.Relationship with the environment. In terms of environmental conditions, it can be subdivided into multiple aspects such as temperature and nutrition, so as to describe the changes in the environment under the influence of lamprey populations. where Zt denotes the environmental conditions, and Z1t and Z2t denote the temperature and nutrients

\( \frac{d{Z_{1t}}}{dt}={i_{1}}-{j_{1}}{X_{t}}-{k_{1}}{Y_{1t}}-{l_{1}}{Y_{2t}} \)

\( \frac{d{Z_{2t}}}{dt}={i_{2}}-{j_{2}}{X_{t}}-{k_{2}}{Y_{1t}}-{l_{2}}{Y_{2t}} \)

3.2.4.Advantages and disadvantages of the sex ratio change model.

\( \frac{d{x_{f}}}{dt}={b_{1}}(F,{X_{m}}){X_{f}}-{C_{1}}{X_{f}}-{a_{11}}{X_{f}}{P^{ \prime }} \)

\( \frac{d{x_{m}}}{dt}={b_{2}}(F,{X_{f}}){X_{m}}-{C_{2}}{X_{m}}-{a_{12}}{X_{m}}{P^{ \prime }} \)

\( \frac{dF}{dt}=g({X_{f}},{X_{m}})-{hF-a_{21}}{X_{f}}-{a_{22}}{X_{m}} \)

\( \frac{dp \prime }{dt}=e({a_{21}}{X_{f}}+{a_{22}}{X_{m}}){p^{ \prime }}-C{P^{ \prime }} \)

where Xm_(t) represents the number of male lampreys, Xf_(t) represents the number of female lampreys, and P'_(t).Indicates the number of other species (parasites), C1 and C2 indicate the natural mortality rate of eels, h indicates the rate of natural resource depletion in the ecosystem, C indicates the natural mortality rate of other species (parasites) P', and e indicates the natural growth rate of parasites P'. b1(F,Xm) and b2(F,Xf) both represent the change of the sex ratio adjustment function of the lamprey population with the number of individuals of the opposite sex, and g(X f, X_m) represents the natural growth rate of resource F produced by lamprey individuals.

3.3.Model Analysis

3.3.1.Calculation of the sex ratio. Total lampreys:

\( {X_{t}}={M_{t}}+{F_{t}} \)

Gender Conversion Rate:

\( R={R_{0}}{e^{-Kt}} \)

Specifically, males have a ratio of Mn to females to Fn

3.3.2.Dynamic models of quantitative variation.

1.Kinetic model of the overall quantity change

\( \frac{d{x_{t}}}{dt}=b(T-t,Rt,t,St)({M_{t}}+{F_{t}})-d(T-t,Rt,t,St)({M_{t}}+{F_{t}}) \)

2.Kinetic model of male number change

\( \frac{{dm_{t}}}{dt}=b(|T-t|,Rt,t,St){M_{t}}-d(|T-t|,Rt,t,St){M_{t}} \)

3.A dynamic model of changes in the number of women

\( \frac{{dF_{t}}}{dt}=b(|T-t|,Rt,t,St){F_{t}}-d(|T-t|,Rt,t,St){F_{t}} \)

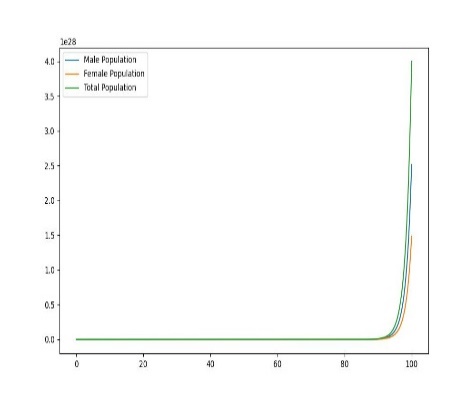
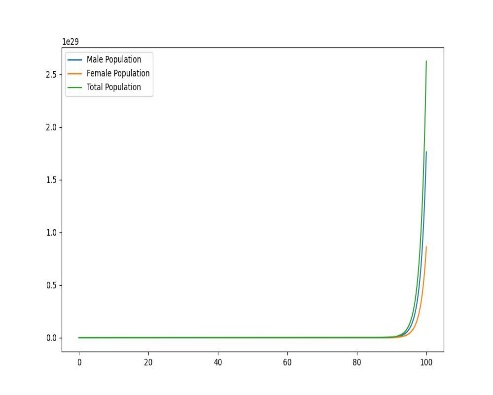
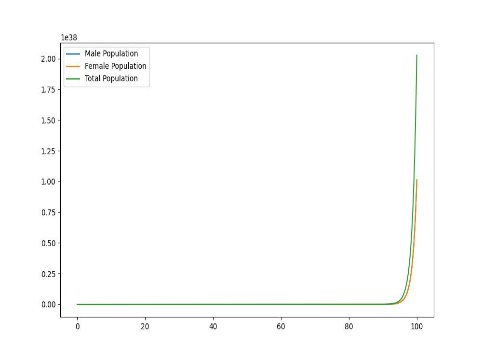
Figure 1. Dynamic plot of birth and mortality rates of sea lampreys

In order to explore the dynamic effects of the population as a whole on birth and mortality, it is assumed that after distribution, as shown in the figure, there will be uneven changes in the birth and mortality rates of female lampreys, with food scarcity and prey prey leading to increased mortality, and due to the imbalance in their sex ratio affecting fertility, the offspring birth rate will decrease, and only when the birth rate is the same, the two will produce the same sex ratio.

3.3.3.Dynamic models of food sources.

1.Holistic food source dynamics model

\( \frac{d{G_{t}}}{dt}=g({G_{t}}，{M_{t}}+{F_{t}}){G_{t}}-h({G_{t}},{M_{t}}+{F_{t}}){G_{t}} \)

2.Kinetics of male food sources

\( \frac{d{G_{mt}}}{dt}=g({G_{t}}，{M_{t}}){G_{t}}-h({G_{t}},{M_{t}}){G_{t}} \)

3.Kinetic models of female food sources

\( \frac{d{G_{ft}}}{dt}=g({G_{t}}，{F_{t}}){G_{t}}-h({G_{t}},{F_{t}}){G_{t}} \)

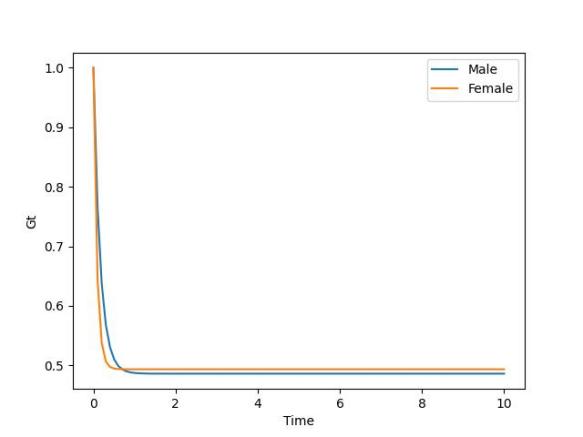
Figure 2. Rate of change in food source of sea lamprey

In order to explore the effect of lamprey food source on the sex ratio of lampreys, the analysis results are shown in Figure 2, the number of female and male lampreys decreased over time, but the decline rate of female lampreys was significantly faster than that of male lampreys, and the sex ratio of both decreased, and the sex ratio would tend to be balanced.

3.3.4.Dependent population model.

1.Population-dependent population dynamics model

\( \frac{d{p_{t}}}{dt}=p({G_{t}},{M_{t}}+{F_{t}}){p_{t}}-q({G_{t}},{M_{t}}+{F_{t}}){p_{t}} \)

2.Male-dependent population dynamics model

\( \frac{d{p_{mt}}}{dt}=p({G_{t}},{M_{t}}){p_{t}}-q({G_{t}},{M_{t}}){p_{t}} \)

3.Female-dependent population dynamics model

\( \frac{d{p_{ft}}}{dt}=p({G_{t}},{F_{t}}){p_{t}}-q({G_{t}},{F_{t}}){p_{t}} \)

3.3.5.Environmental impact of changes in the sex ratio. Temperature effects

\( {f_{1}}(|T-t|)={R_{0}}{e^{-{K_{1}}t}} \)

Nutritional effects

\( {f_{2}}(N)=\frac{{R_{0}}}{(1+}\frac{{K_{2}}}{N}) \)

EFFECT ON PH VALUE

\( {f_{3}}(PH)=\frac{{R_{0}}}{(1+}\frac{{K_{3}}}{(PH-P{H_{0}})}) \)

Effects on oxygen in nature

\( {f_{4}}({O_{2}})=\frac{{R_{0}}}{(1+}\frac{{K_{3}}}{({O_{2}}-{O_{20}})}) \)

Effects on heavy metals in nature

\( {f_{5}}(C)={R_{0}}{e^{-{K_{5}}c}} \)

Effect on salinity

\( {f_{6}}(S)=\frac{{R_{0}}}{(1+}\frac{{K_{6}}}{(S-{S_{0}})}) \)

Effect on turbidity

\( {f_{7}}(O)=\frac{{R_{0}}}{(1+}\frac{{K_{7}}}{O}) \)

Total environmental impact

3.3.6.Advantages and disadvantages of changes in the sex ratio.

3.3.6.1.Impact on intermediate hosts.

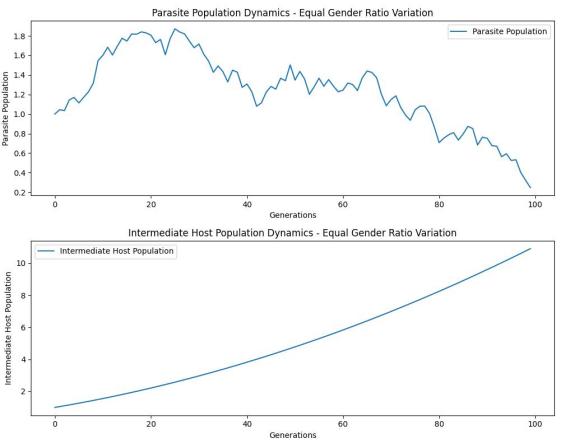
Figure 3. Effect of sex ratio on intermediate hosts in lampreys

In terms of the relationship between the sex ratio of lampreys and intermediate hosts, we also made a preliminary speculation that the reason for the continuous increase in the number of intermediate hosts may be due to the small number of lamprey populations in the current environment, which not only reaches the environmental capacity, but also does not pose a threat to the stability of the ecosystem.

3.3.6.2.Relationship with the number of subpopulations of other species.

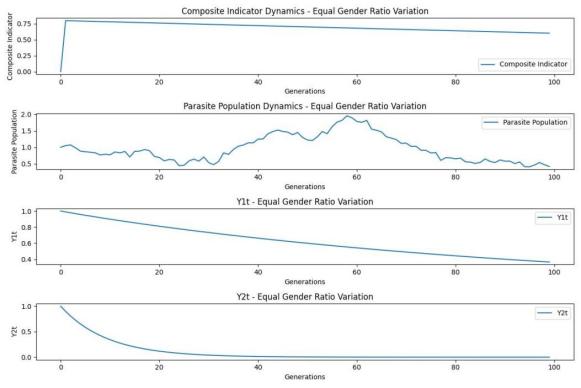
Figure 4. Sex ratio and number of other species in lampreys

Similarly, as shown in Figure 4, when the lamprey reproduces to about 5 generations, the Y-axis value is lower than 0.75 (we believe that 0.75 may be the environmental carrying capacity of the environment at that time), and the entire lamp eel population is stable for the ecosystem.

In the sex ratio of lamprey and other species, with the increase of lamprey population generations, other species subpopulations tend to decrease, which may indicate that the invasion of lampray species may pose a threat to some species, which is not conducive to the stability of local ecosystems, and it is difficult to provide advantages for other species subpopulations.

3.3.6.3.Relationship with the environment.

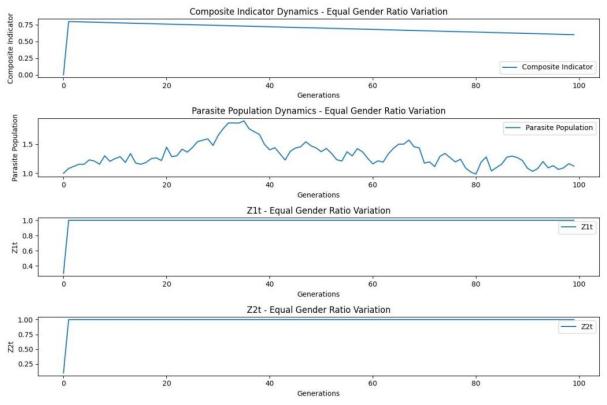
Figure 5. Sex ratio and environment of domestic lampreys

Similarly, as shown in Figure 5, when the lampreys multiplied around 5 generations, the Y-axis value was below 0.75 (we thought that 0.75 may have been the environmental carrying capacity of the environment at that time), and the entire lamprey population was stable for the ecosystem.

In terms of the sex ratio and environment (e.g., temperature, nutrition, etc.) of lamprey, it can be seen from the figure that as the lamprey population increases from generation to generation, the environmental conditions tend to be saturated, which will help the survival and reproduction of other species populations, and in essence, the lampll eel population is indirectly to other species, which helps to maintain the stability of the ecosystem.

3.3.6.4.Model fitting. Finally, the lamprey sex ratio St is introduced into each equation as a variable. The specific models are as follows:

\( \frac{d{W_{t}}}{dt}=m{W_{t}}-n({S_{t}}){X_{t}}{W_{t}} \)

\( \frac{d{Y_{it}}}{dt}={e_{i}}{Y_{it}}-{f_{i}}{({S_{t}})X_{t}}{Y_{it}}-{g_{i}}{Y_{it}}{Y_{jt}}(i≠j) \)

\( \frac{d{Z_{it}}}{dt}={i_{i}}-{j_{i}}{({S_{t}})X_{t}}-{k_{i}}{Y_{it}}-{l_{i}}{Y_{jt}}(i≠j) \)

Therefore, in addition to maintaining ecosystem stability, changes in the sex ratio of lampreys can provide the following benefits:

10.In terms of ecological environment, the adjustment of the sex ratio of lamprey population under certain environmental conditions will help promote the development of the local environment to the best state, and at the same time, other species can use local resources more flexibly, reduce the competition for resources between species, and better provide nutrients for the survival and reproduction of other species, so as to maintain the balance of the ecosystem.

11.When the individual competitiveness of the lamprey population is strong, a certain number of lampray populations may migrate, reduce the risk of excessive resource pressure on the population in the region, and also help to provide new living space for other species or reduce the spatial pressure of the original habitat by changing the use of habitats, so as to maintain a stable ecological environment.

3.3.7.Coupled ecodynamics model.

\( \frac{dX}{dt}={r_{X}}(1-\frac{X}{k})-{Z_{X}}{M_{X}}-{d_{X}}(1-M) \)

\( \frac{dM}{dt}=a(b-M)-e{M_{X}} \)

\( \frac{dP \prime }{dt}=f{M_{X}}-gP \prime \)

The numerical results of the analysis are shown in Figure 6, showing the effect of the lamprey sex ratio M on the number of parasites P′

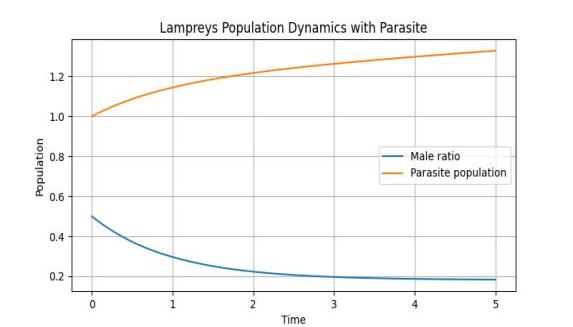
Figure 6. Effect of sex ratio on parasite populations in lampreys

In order to explore the effect of lamprey food source on the sex ratio of lampreys, the analysis results are shown in Figure 6, the number of female and male lampreys decreases over time, but the decline rate of female lampreys is significantly faster than that of male lampreys, and the sex ratio will tend to be balanced when both are reduced to about 0.5.

3.3.8.Advantages and disadvantages of changes in the sex ratio

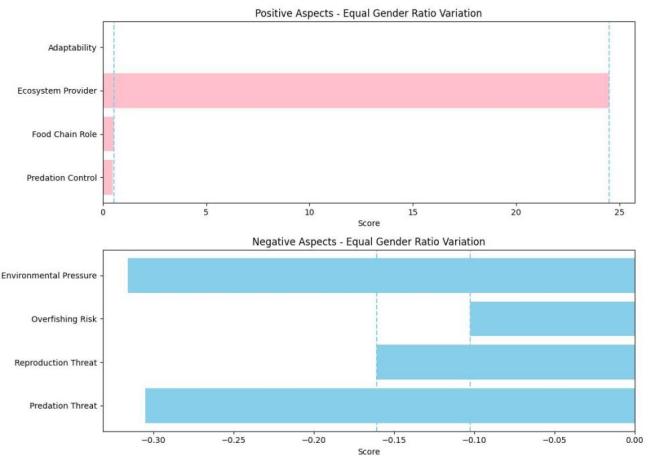
Figure 7. Strengths and weaknesses of lamprey populations

The results of the analysis are shown in Figure 7. At the top of the figure is the dominance of the lamprey population, indicating that the lamprey population has a significant advantage in terms of ecosystem provider and no advantage in terms of adaptability, indicating that the lampray population is less adaptable to the environment. At the bottom of the plot are the disadvantages of lamprey populations, with the greatest disadvantage for environmental pressures and the least disadvantage for overfishing risk.

4.Conclusion

Based on the diversity of ecosystem and interspecies interactions, the modeling of ecosystems and related dynamics have been widely studied. With the deepening of nonlinear theory, the depiction of ecosystem models is not only limited to ordinary differential models, but also fractional calculus and reaction diffusion terms are more introduced into ecosystem models to characterize the regular or irregular migration process of species in space, and the interaction between populations [4].

In this paper, the effects of different sex ratios of sea lamprey on the ecosystem and other populations within the ecosystem are analyzed in detail. In this paper, a logistics regression model, an adjoint model and an ecological dynamics model are developed. To this end, the following conclusions are drawn.

12.As an important member of the ecosystem, changes in the sex ratio of sea lamprey may affect its own reproductive rate and population size, and also directly or indirectly lead to the number and distribution of other dependent populations, which in turn affects the stability of the ecosystem. In particular, when the sex ratio is unbalanced, it is easy to cause environmental imbalance in the ecosystem and cause irreversible negative impacts on the ecosystem.

13.In the case of changes in the sex ratio of lampray population, for the whole ecosystem, lamprey population helps to improve the resource utilization efficiency of the ecosystem and maintain the ecological balance of the ecosystem. For human beings, it also has certain economic and cultural value. From the disadvantages, for the whole ecosystem, the lamp eel population is highly dependent on the ecological environment, and when the sex ratio is unbalanced, it will lead to the imbalance of the ecosystem, and the lamprey as an intermediate host, there are also certain potential threats.

14.As an important member of the food chain in the ecosystem, lampreys play an important role in maintaining the stability of the ecosystem. Proper proportions and appropriate conditions will affect how other species in the ecosystem survive and reproduce, thereby maintaining species diversity in the ecosystem.

15.Changes in the sex ratio of lampray populations in the food chain of ecosystems may involve issues upstream and downstream in the food chain, the relationship of lampray populations to other species, the increase in parasites, the survival and reproduction of parasite populations, and changes in the sex ratio of lamprey populations will provide some species but may also adversely affect some species, but the specific situation should depend on the complex interactions between ecosystems and species.