1 Introduction

The moment of inertia is a physical quantity that describes an object's resistance to rotational motion. It is crucial for understanding and analyzing the rotational motion of rigid bodies. Accurately measuring and comprehending an object's moment of inertia is indispensable in many engineering and scientific fields. In the past, various methods were used to measure moment of inertia, including simple geometric measurements, rotating test benches, as well as more complex devices and techniques. However, with the development of science and technology, there is an increasing demand for more precise measurement of moment of inertia. Particularly in the micro-worlds and high-precision engineering fields, there are stricter requirements for measuring moment of inertia.

Recently, much attention has been paid to measuring moments of inertia with new methods and technologies to improve measurement accuracy while reducing sources of error during experiments. These studies have important implications for advancing developments in science and engineering fields.

In 2004, Sheng et al. discussed on the impact of approximations employed in formulating the rotational inertia measurement equation, and proposed strategies to mitigate their influence on measurement outcomes [1]. In 2006, Zhang and Hou conducted a study on the measurement of rotational inertia in three-line pendulums considering the stretching effect of trochoids. With a comprehensive differential equation, it was possible to quantitatively investigate the impact of small angle approximation and absence of elastic deformation assumption on the accuracy of actual measurements [2]. In 2003, Song et al. by conducting experimental tests and comparing them with the theoretical exact values, the author revealed that the length of the cycloid is a major influencing factor in determining the accuracy of measuring an object's moment of inertia using the three-wire pendulum method [3]. In 2019, Bin et al. discussed the research significance and current status of the three-line method in measuring rotational inertia [4]. More interesting moments of inertia for irregular objects can be seen in [5-8]. Moments of inertia have numerous applications in disciplines such as physics [9,10].

The purpose of this article is to explore the measurement methods of rotational inertia and its applications in the fields of science and engineering. Some common methods for measuring rotational inertia are introduced. By delving into the measurement methods and techniques of rotational inertia, the nature of rotational motion can be better understood and more reliable data and approaches for engineering design and scientific research can be provided.

2 Method

2.1 Method for calculating the moment of inertia of a simple model

The moment of inertia is also called the mass moment of inertia, or the moment of inertia. The moment of inertia is a measure of the inertia for an object when it rotates around an axis. The moment of inertia describes the inertia of an object during its motion around a certain axis. For an object whose mass is distributed in space, the moment of inertia is defined as

\( I=\int_{}^{} r^{2}dm \) (1)

\( I \) represents the moment of inertia, \( r \) signifies the distance from a single particle to the axis of rotation and \( dm \) denotes the volumetric microelement in calculating moment of inertia. Formula (1) is only applicable to relatively simple objects with regular shapes, such as the moment of inertia for a rigid rod rotating about one end and for a rigid sphere rotating about its diameter.

Here is an example of calculating the moment of inertia for a rigid rod rotating about one end in Figure 1. Suppose there is a uniform rigid rod with length R and line density \( λ \) . The moment of inertia can be calculated using a formula. For a uniform rigid rod, its moment of inertia is determined by

\( I=\int_{0}^{R} dm∙r^{2}=\int_{0}^{R} λr^{2}dr=\frac{1}{3}λR∙R^{2}=\frac{1}{3}MR^{2} \) (2)

When rotating around the vertical axis and passing through the midpoint of this slender rod leads to that:

\( I=\int_{-R/2}^{R/2} λ∙dr∙r^{2}=\int_{-R/2}^{R/2} dm∙r^{2}=[\frac{1}{3}λr^{3}]\frac{R/2}{-R/2}=\frac{1}{3}λ(\frac{R^{3}}{8}+\frac{R^{3}}{8})=\frac{1}{12}MR^{2} \) (3)

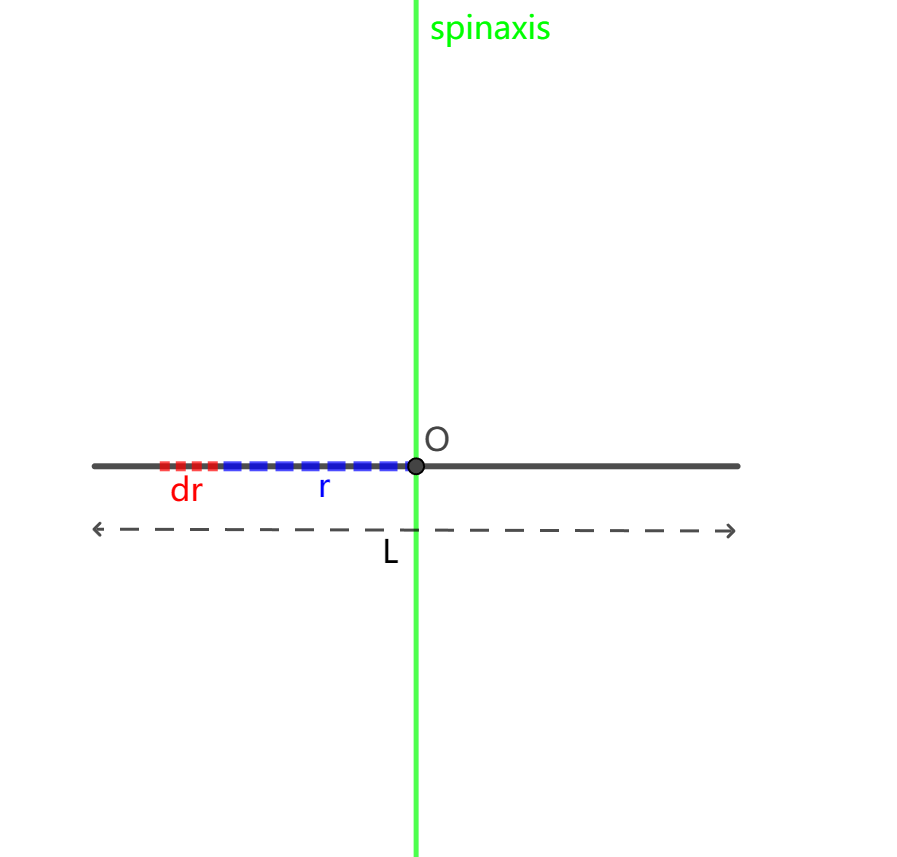
Figure 1. A rigid rod rotates around its midpoint

Now, the moment of inertia of a thin spherical shell rotating around its diameter is considered in Figure 2. Consider a uniform thin spherical shell with radius R and mass M rotating about its diameter axis. In this case, the shell can be viewed as a stack of countless circular rings. Let the thickness of the shell be \( ω \) , width of each ring be \( dθ∙R \) , and distance from a point on the ring to the axis of rotation be \( r, r=R∙sin{θ} \) . The rotational inertia of a homogeneous thin spherical shell can then be calculated using a formula. First, the rotational inertia for each individual circular ring needs to be calculated.

\( I_{ring}=ρ∙dθ∙R∙ω∙2πr∙r^{2}=ρ∙dθ∙R∙ω∙2π∙R∙sin{θ}∙(R∙sin{θ})^{2} \)

\( V=R∙dθ∙ω∙2πr \) (4)

Next, author will calculate the moment of inertia for the rotation of a spherical shell.

\( I_{shell}=\int_{0}^{π} ρ∙R^{4}ω2πsin^{3}θdθ=ρR^{4}ω2π\int_{0}^{π} sin^{3}θdθ=ρR^{4}ω2π\int_{0}^{π} (1-cos^{2}θ)sinθdθ \) (5)

Set \( u=cosθ \) and \( du=-sinθdθ \) , when \( θ=0,π \) , \( u=1,-1. \)

\( I_{shell}=ρR^{4}ω2π\int_{1}^{-1} (1-u^{2})du=ρR^{4}ω2π[u-\frac{1}{3}u^{3}]\frac{1}{-1}=\frac{2}{3}ρ∙4πR^{2}∙ω∙R^{2}=\frac{2}{3}mR^{2} \) (6)

The rotational inertia of a sphere will be Calculated in Figure 3. The sphere can be regarded as a stack of countless extremely thin (neglecting thickness) circular slices, in order to calculate the integral by layering these circular slices. Each circular slice can be seen as composed of numerous thin circular rings. Let the radius of the thin circular ring be \( x \) , its thickness be \( dx \) , and the radius of the circular slice be \( r \) . The mass density is denoted as \( ρ \) , and the distance from the center of the circle to each circular slice is represented by \( y \) . With a thickness of \( dy \) , and considering that the sphere has a radius of \( R \) , the radius of each circular slice is \( r=\sqrt[]{R^{2}-y^{2}} \) . The expression for rotational inertia for each individual circular slice is:

\( I_{disk}=\int_{0}^{\sqrt[]{R^{2}-y^{2}}} ρ∙2πx∙dx∙dy∙x^{2}=[\frac{1}{2}ρπx^{4}dy]\frac{\sqrt[]{R^{2}-y^{2}}}{0}=\frac{1}{2}ρπ(R^{2}-y^{2})dy \) (7)

Calculating the moment of inertia for the entire sphere leads to

\( I_{sphere}=\int_{-R}^{R} \frac{1}{2}ρπ(R^{2}-y^{2})^{2}dy=\frac{1}{2}ρπ\int_{-R}^{R} (R^{4}-2R^{2}y^{2}+y^{4})dy=ρ\frac{8}{15}πR^{5} \)

\( =\frac{2}{5}∙ρ∙\frac{4}{3}πR^{3}∙R^{2}= \frac{2}{5}mR^{2 } \) (8)

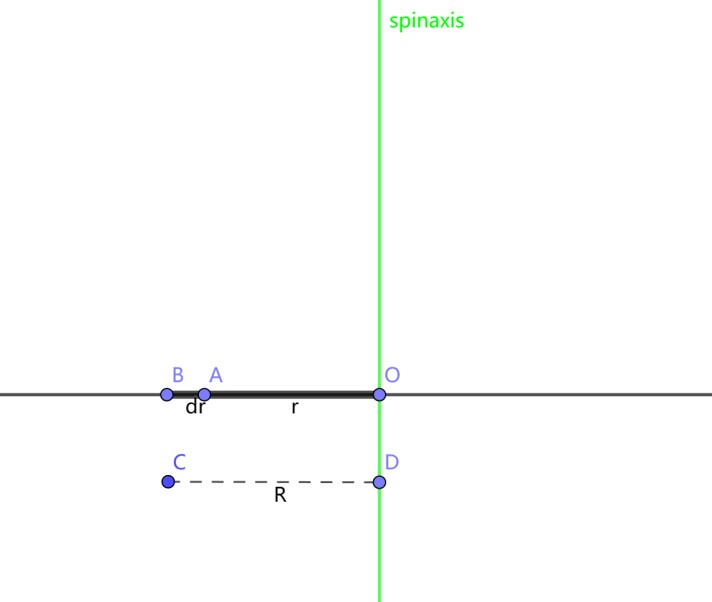
Figure 2. A rigid rod rotates around one of its ends

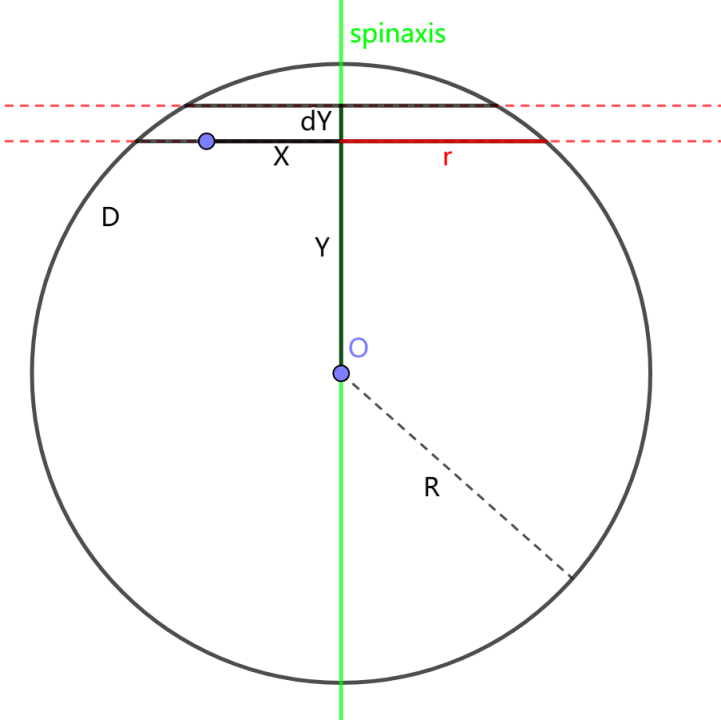
Figure 3. The sphere rotates around its diameter

The moment of inertia of a sphere in Figure 4 will be calculated. Assume that the volume of the sphere is \( V \) , the radius is \( r \) , and its body density is \( ρ=M/(4πR^{3}/3) \) . Consider the sphere as a composition of countless thin spherical shells. Suppose the radius of the \( i \) spherical shell is \( r_{i} \) , the thickness is \( dr \) , the volume is \( 4πr^{2}dr \) , and its total moment of inertia is:

\( I=\int_{0}^{R} \frac{2}{3}r^{2}dm=\frac{2}{3}ρ\int_{0}^{R} r^{2}dV=\frac{2M}{R^{3}}\int_{0}^{R} r^{4}dr=\frac{2}{3}MR^{2} \) (9)

The moment of inertia of a cylinder will be calculated in Figure 5. Before calculating the rotational inertia of the cylinder, first calculate the rotational inertia of the thin disk. Let a disk be The radius is r, the area is 2, and the total moment of inertia is

\( I=\int_{0}^{R} r^{2}dm=\int_{0}^{R} r^{2}σ∙2πrdr \) = \( 2πσ\int_{0}^{R} r^{3}dr \) (10)

The cylinder can be regarded as composed of countless thin disks, and the moment of inertia is

\( I=\int_{0}^{2π} \int_{0}^{R} σr^{2}∙r drdθ=2πσ\int_{0}^{R} r^{3}dr=\frac{1}{2}σπR^{2}R^{2}=\frac{1}{2}MR^{2} \) (11)

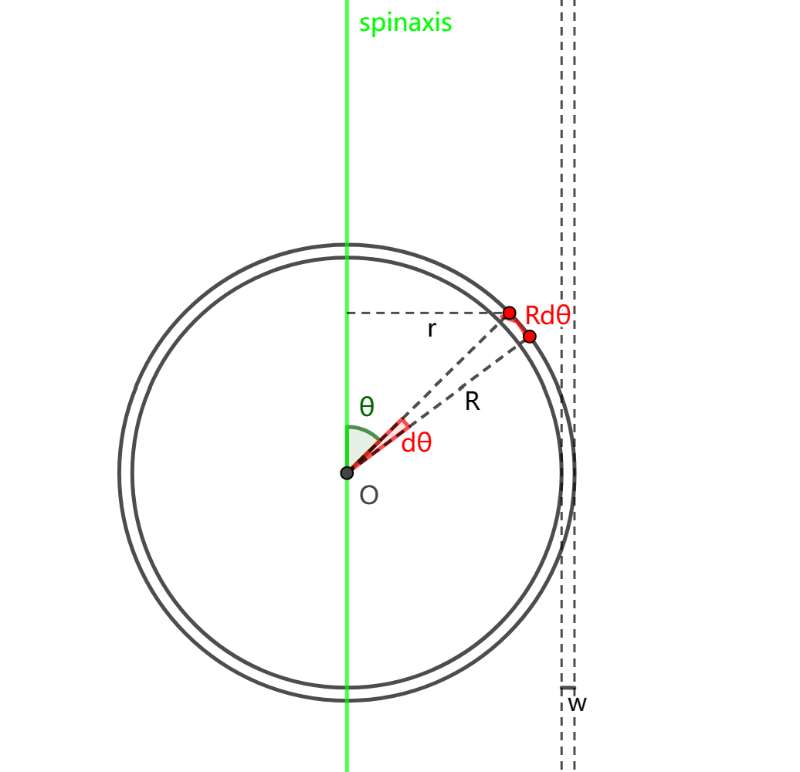
Figure 4. A sphere rotating around its diameter

Figure 5. The cylinder rotates around its axis

2.2 Calculation of Moment of Inertia using Multiple Integrals

The moment of inertia for a uniformly dense annulus about an axis perpendicular to the central axis of the annular plane will be Calculated in Figure 6. Let the ring \( D \) be \( R_{1}^{2}≤x^{2}+y^{2}≤R_{2}^{2} \) , with a density of \( ρ \) and a mass of \( m=ρ∙(πR_{2}^{2}-πR_{1}^{2}) \) . Taking any point \( P(x,y) \) on the ring, at a distance \( \sqrt[]{x^{2}+y^{2}} \) from its \( z \) -axis, its moment of inertia is:

\( J=\int_{}^{} \int_{D}^{} ρ∙(x^{2}+y^{2})dσ=ρ\int_{0}^{2π} dθ\int_{R_{1}}^{R_{2}} r^{3}dr=\frac{πρ}{2}(R_{2}^{4}-R_{1}^{4})=\frac{m}{2}(R_{2}^{2}+R_{1}^{2}) \) (12)

The rotational inertia of a uniform disk about its diameter will be calculated in Figure 7. Let the disk \( D \) be \( x^{2}+y^{2}≤R^{2} \) , with a density of \( ρ \) and a mass of \( ρ=πR^{2} \) . Calculate the moment of inertia for circular disk \( D \) rotating about its diameter. The moment of inertia for any point \( P(x,y) \) within the disk at a distance \( |x| \) from the axis is:

\( J=\int_{}^{} \int_{D}^{} ρx^{2}dσ=ρ\int_{0}^{2π} dθ\int_{0}^{R} (rcos{θ})^{2}∙rdr=ρ\int_{0}^{2π} cos^{2} θdθ∙\int_{0}^{R} r^{3}dr∙rdr=\frac{ρπR^{4}}{4} \)

\( J=\frac{1}{4}mR^{2} \) (13)

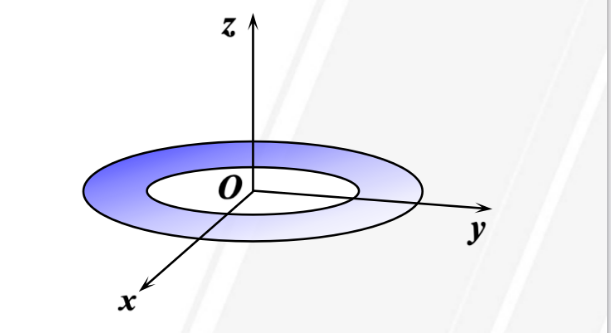
Figure 6. Rotate around the axis perpendicular to the central axis of the annular plane

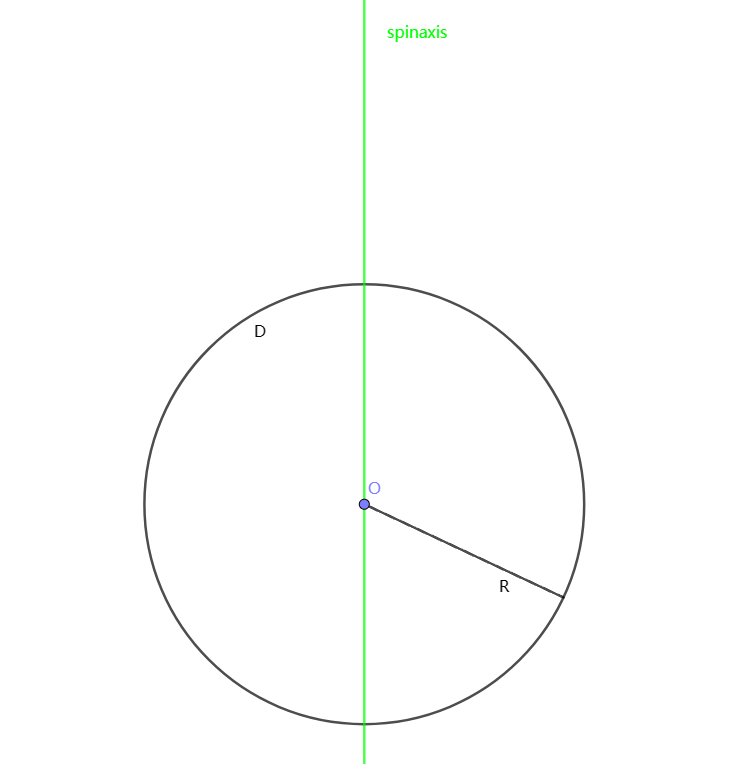
Figure 7. A uniform disk rotates around its diameter

A sphere in which the density is proportional to the distance from each point to the center, has a moment of inertia about its tangent plane.

Let the sphere be represented by an inequality \( x^{2}+y^{2}+z^{2}≤R^{2} \) , where the relationship \( ρ=k\sqrt[]{x^{2}+y^{2}+z^{2}} \) between the density at each point and its distance to the center of the sphere is defined. Let \( k \) be a proportional constant and the equation of the tangent plane is \( x=R \) . The moment of inertia of the sphere with respect to this plane is

\( J=k\iiint_{V}^{} \sqrt[]{x^{2}+y^{2}+z^{2}}∙(R-x)^{2}dxdydz =k\int_{0}^{2π} dθ\int_{0}^{π} dφ\int_{0}^{R} (R-rsinφcosθ)^{2}∙r∙r^{2}sinφdr=kR^{2}\int_{0}^{2π} dθ\int_{0}^{R} r^{3}dr\int_{0}^{π} sinφdφ-2kR\int_{0}^{2π} cosθdθ\int_{0}^{R} r^{4}dr\int_{0}^{π} sin^{2}φdφ+k\int_{0}^{2π} cos^{2}θdθ\int_{0}^{R} r^{5}dr\int_{0}^{π} sin^{3}φdφ \)

\( J=\frac{11}{9}kπR^{6} \) (14)

3 Conclusion

In conclusion, the measurement of moment for inertia is essential for understanding and analyzing the rotational motion of rigid bodies in various engineering and scientific fields. Over the years, significant efforts have been made to develop precise measurement methods and techniques to accurately determine moment of inertia while minimizing experimental errors. Several studies discussed in this article have shed light on the importance of considering various factors, such as approximations in equations, elastic deformations, and the length of cycloids, in measuring moment of inertia using different methods, particularly the three-line pendulum method. Researchers have proposed strategies and optimization schemes to mitigate the influence of these factors on measurement outcomes, thus enhancing the accuracy and reliability of experimental results. These efforts have advanced developments in science and engineering, providing valuable insights into the nature of rotational motion and contributing to the improvement of engineering design and scientific research. Moving forward, continued research and innovation in measurement techniques and error reduction methods will further enhance our understanding of moment of inertia and its applications. By continually refining measurement methods and techniques, the accuracy and reliability of experimental data, facilitating advancements in science, engineering, and technology will be improved in the future.