1. Introduction

Quantum entanglement has been used to various quantum protocols such as teleportation and dense coding assisted by classical channels [1,2]. Ref. [3,4] showed the operational principles and mathematical foundations of several existing quantum communication protocols. Besides, quantum protocols can also be used for classical computers [5]. Current existing classical encryption methods are no longer entirely secure, as methods for rapidly breaking classical encryption have been proposed [6]. After addressing issues such as decoherence and noise [7,8], the unique advantages of quantum encryption are gradually becoming apparent [9,10]. Subsequently, researchers investigated practical steps for quantum information transmission protocols, aiming to reduce costs and enhance efficiency [11]. Next, the quantum cost of dense coding and teleportation protocols has been evaluated in terms of CNOT gates [12]. Authors in [13] showed that the quantum remote control may be applied to realize the teleportation unitary gates. Further, the similar technique has been used to teleport angles with a secure way [14]. Further, multipartite scenarios have been considered for a deterministic single-qubit. That is, recent advancements in the field of remote implementation of partially unknown quantum operations on multiple qubits have led to significant breakthroughs, rendering practical operations feasible. These developments have substantially propelled the potential applications of quantum communication and networking forward [15]. Besides, operation sharing with five-qubit cluster state has been established [16,17]. These operations and protocols provide a good foundation for realizing more complex protocols of transmitting information securely.

In this paper, we develop the above protocols by constructing a multi-party quantum security protocol in terms of the so-called remote-controlled implementation of operations. In Sec. II, we delve into the CNOT gate, Hadamard Gate, and the Kronecker product. Subsequently, we provide a detailed exposition on the operational mechanisms of current quantum dense coding and quantum stealth coding protocols. In Sec. III, we discuss a quantum Quantum Communication Protocols, which Bob send massage to Charlie and Alice have ability to control the message transmit. Then in Sec. IV, by redesigning the communication protocol, we achieve the controlled communication among Alice, Bob, Charlie, and Daniel. Alice measures her qubit, and then the receiver Charlie and Daniel both measure their qubit. As a result, Bob, Charlie and Daniel share a stator of particles b, C and D. Then Bob can perform a local unitary gate containing a parameter unknown to Alice, Charlie and Daniel. We finally conclude in Sec. V.

2. Preliminaries

In this section, we review the preliminary knowledge for this paper. In Sec. II A, we review the notion of Kronecker product and its basic properties. In Sec. II B, we review the Hadamard gate, controlled NOT gate and Bell states and so on. In Sec. II C we introduce the protocol of quantum super dense coding. In Sec. II D, we introduce the protocol of quantum teleportation.

2.1. Kronecker product

The Kronecker product is a computational method that allows for the multiplication of any two matrices without the constraints on the number of rows and columns. The following matrices are given.

\( A=(\begin{matrix}{a_{11}} & {a_{12}} & ⋯ & {a_{1n}} \\ {a_{21}} & {a_{22}} & ⋯ & {a_{2n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ {a_{m1}} & {a_{m2}} & ⋯ & {a_{mn}} \\ \end{matrix}),B=(\begin{matrix}{b_{11}} & {b_{12}} & ⋯ & {b_{1q}} \\ {b_{21}} & {b_{22}} & ⋯ & {b_{2q}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ {b_{p1}} & {b_{p2}} & ⋯ & {b_{pq}} \\ \end{matrix}) \) .

Then we define the Kronecker product

\( A⊗B=(\begin{matrix}{a_{11}}B & {a_{12}}B & ⋯ & {a_{1n}}B \\ {a_{21}}B & {a_{22}}B & ⋯ & {a_{2n}}B \\ ⋮ & ⋮ & ⋱ & ⋮ \\ {a_{m1}}B & {a_{m2}}B & ⋯ & {a_{mn}}B \\ \end{matrix}). \)

We describe the following properties.

(1) If matrix A is an \( m×n \) matrix, and the matrix B is a \( p×q \) matrix, then the Kronecker product of the matrices \( A \) and \( B \) is defined above, regardless of the size of \( A \) and \( B \) . In other word, the Kronecker product of A and B, denoted \( A⊗B \) , is an \( mp×nq \) matrix, resulting from multiplying every element of \( A \) by matrix \( B \) . Similarly, the Kronecker product of B and A, denoted \( B⊗A \) , is a \( pm×qn \) matrix, resulting from multiplying every element of \( B \) by matrix \( A \) .

(2) Next, we introduce the distributive property. The Kronecker product has a distributive property over addition, \( A⊗(B+C)=A⊗B+A⊗C \) .

(3) Third, the mixed product property of Kronecker product is \( (A⊗B)(C⊗D)=(AC)⊗(BD) \) .

(4) Four the transpose property of Kronecker product is \( {(A⊗B)^{T}}={A^{T}}⊗{B^{T}} \) .

(5) Finally the scalar multiplication property is \( c(A⊗B)=(cA)⊗B=A⊗(cB) \) .

2.2. Gates and states

We introduce the Hadamard gate as follows.

\( H=\frac{1}{\sqrt[]{2}}[\begin{matrix}1 & 1 \\ 1 & -1 \\ \end{matrix}]. \) (1)

The Hadamard operation can transform the qubit \( |0⟩ \) and \( |1⟩ \) into their superposition with equal weights. The specific formula is as follows.

\( H|0⟩=\frac{|0⟩+|1⟩}{\sqrt[]{2}}, \) (2)

\( H|1⟩=\frac{|0⟩-|1⟩}{\sqrt[]{2}}. \) (3)

Next, the CNOT gate is a quantum gate capable of transforming quantum states in the form of \( |a,b⟩ \) into \( |a,a⊕b⟩ \) where \( a,b=0,1 \) . The operating principle of the CNOT gate is to take the first qubit as the control qubit, and perform the opposite transformation on the second qubit based on the state of the control qubit. It is important to note that the CNOT gate cannot operate on individual quantum states, as it automatically considers the first qubit as the decision maker. The CNOT gate has the matrix form as follows.

\( CNOT=[\begin{matrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{matrix}]. \) (4)

There are four forms of Bell states, each of which is a maximally entangled state of two quantum bits. The properties of entanglement are used to transfer information in the following quantum communication. The specific formula of four Bell states are as follows.

\( |{Φ^{+}}⟩=\frac{1}{\sqrt[]{2}}(|00⟩+|11⟩), \) (5)

\( |{Φ^{-}}⟩=\frac{1}{\sqrt[]{2}}(|00⟩-|11⟩), \) (6)

\( |{Ψ^{+}}⟩=\frac{1}{\sqrt[]{2}}(|01⟩+|10⟩), \) (7)

\( |{Ψ^{-}}⟩=\frac{1}{\sqrt[]{2}}(|01⟩-|10⟩). \) (8)

2.3. Quantum Dense Coding

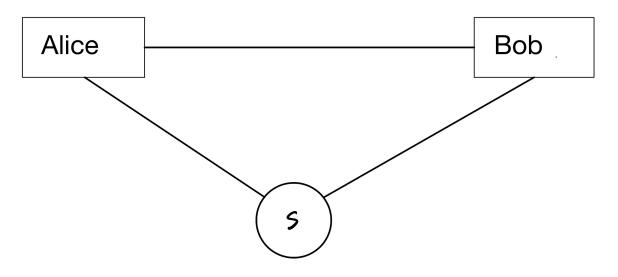
Figure 1. The source S builds an EPR pair and sends the two particles of the pair to Alice and Bob, respectively

The dense coding protocol is presented in Figure 1. The EPR pair has the expression

\( |{ϕ^{+}}⟩=\frac{|00⟩+|11⟩}{\sqrt[]{2}}. \) (9)

Using the Hadamard gate assisted by the CNOT gate implemented in the product state \( |0,0⟩ \) , we can prepare the EPR pair as follows.

\( CNOT(H⊗I)|00⟩=|{ϕ^{+}}⟩. \) (10)

Subsequently, the Hermitian and unitary properties of the Pauli matrices are utilised for information encryption. There are four distinct scenarios, respectively corresponding to the transmission of message states \( |00⟩ \) , \( |01⟩ \) , \( |10⟩ \) , and \( |11⟩ \) . The specific cases are as follows.

First. The message state is \( |00⟩ \) .

\( I⊗I|{ϕ^{+}}⟩=|{ϕ^{+}}⟩. \) (11)

Hence, Alice does nothing from her side. Mathematically, the physical operation is represented by the identity matrix as above.

Second. The message state is \( |01⟩ \) .

\( {σ_{x}}⊗I|{ϕ^{+}}⟩=|{ϕ^{+}}⟩. \) (12)

The calculation detail is as follows.

\( [\begin{matrix}0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{matrix}]\cdot \frac{1}{\sqrt[]{2}}[\begin{matrix}1 \\ 0 \\ 0 \\ 1 \\ \end{matrix}]=\frac{1}{\sqrt[]{2}}[\begin{matrix}0 \\ 1 \\ 1 \\ 0 \\ \end{matrix}]. \) (13)

Third. The message state is \( |10⟩ \) .

\( {σ_{z}}⊗I|{ϕ^{+}}⟩=|{ϕ^{-}}⟩. \) (14)

The calculation detail is as follows.

\( [\begin{matrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{matrix}]\cdot \frac{1}{\sqrt[]{2}}[\begin{matrix}1 \\ 0 \\ 0 \\ 1 \\ \end{matrix}]=\frac{1}{\sqrt[]{2}}[\begin{matrix}1 \\ 0 \\ 0 \\ -1 \\ \end{matrix}]. \) (15)

Finally. The message state is \( |11⟩ \) .

\( i{σ_{y}}⊗I|{ϕ^{+}}⟩=|{ψ^{-}}⟩. \) (16)

The calculation detail is as follows.

\( [\begin{matrix}0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ \end{matrix}]\cdot \frac{1}{\sqrt[]{2}}[\begin{matrix}1 \\ 0 \\ 0 \\ 1 \\ \end{matrix}]=\frac{1}{\sqrt[]{2}}[\begin{matrix}0 \\ 1 \\ -1 \\ 0 \\ \end{matrix}]. \) (17)

We also need decode the message by inverse operation. That is,

\( {(CNOT(H⊗I))^{-1}}=(H⊗I)CNOT. \) (18)

We record this operator as B. By taking the decoding operator, Bob can finally obtain the correct message.

\( \begin{matrix}B|{ψ^{+}}⟩=|01⟩B,|{ψ^{-}}⟩=|11⟩,B|{ϕ^{+}}⟩=|00⟩,B|{ϕ^{-}}⟩=|10⟩. \\ \end{matrix} \) (19)

2.4. Quantum teleportation

Quantum invisible transmission of states through quantum entanglement of Bell states allows the transmission of quantum information at both ends solely through the classical channel. The principles and methods are as follows.

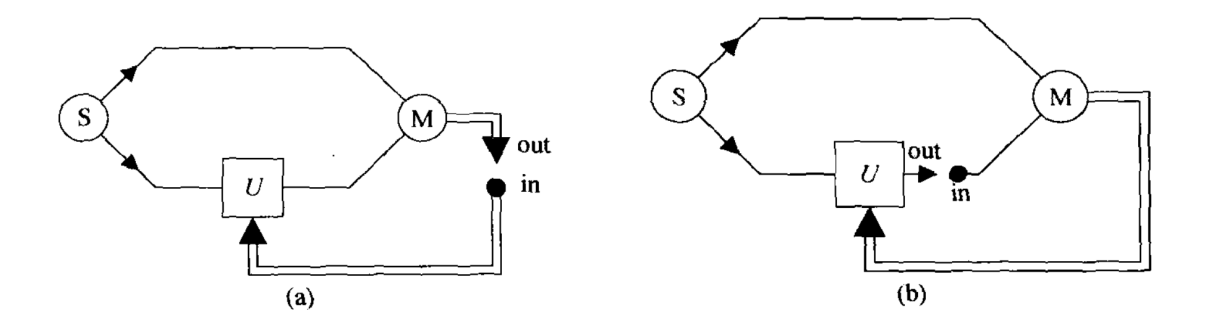
Figure 2. (a) Image content is densely coded (b) for quantum invisible state transfer

Suppose Alice wants to convey to Bob the two-energy-level quantum information that is in a superposition state \( α|0⟩+β|1⟩. \) She can use the second method which is shown in Figure 2.

Step 1. We build the EPR pair.

The source S generates an EPR pair namely a Bell state, and sends the first half to Alice and the second half to Bob. Make sure the pair of quanta is in an entangled state \( |{ψ^{+}}⟩=\frac{1}{\sqrt[]{2}}(|01⟩+|10⟩). \) To build this EPR pair, S should carry out the physical operation as follows.

\( CNOT(H⊗I)|00⟩=|{ψ^{+}}⟩. \) (20)

By sending the EPR pair to Alice and Bob, Alice has two particles, which are respectively half of the EPR pair and the message qubit she wants to transmit to Bob. On the other hand Bob only has one qubit, namely the other half of EPR pair.

The state of the three qubits are given by the tensor product of \( |ψ⟩ \) and \( |{ψ^{+}}⟩ \) as follows.

\( \begin{matrix}|ψ⟩⊗|{ψ^{+}}⟩ & =(α|0⟩+β|1⟩)⊗\frac{1}{\sqrt[]{2}}(|01⟩+|10⟩) \\ & =\frac{α}{\sqrt[]{2}}(|001⟩+|010⟩)+\frac{β}{\sqrt[]{2}}(|101⟩+|110⟩). \\ \end{matrix} \) (21)

Step 2. Joint measurement by Alice.

The reason why Alice needs to do the joint measurement is that if Alice only determines message qubit, this quantum will collapse to \( |0⟩ \) or \( |1⟩ \) . The way out of this problem is to make measurements on the Bell state, i.e., \( |{ϕ^{+}}⟩ \) , \( |{ϕ^{-}}⟩ \) , \( |{ψ^{+}}⟩ \) , \( |{ψ^{-}}⟩ \) .

\( \begin{cases}\begin{matrix}|00⟩ & =\frac{1}{\sqrt[]{2}}(|{ϕ^{+}}⟩+|{ϕ^{-}}⟩), \\ |11⟩ & =\frac{1}{\sqrt[]{2}}(|{ϕ^{+}}⟩-|{ϕ^{-}}⟩), \\ |01⟩ & =\frac{1}{\sqrt[]{2}}(|{ψ^{+}}⟩+|{ψ^{-}}⟩), \\ |10⟩ & =\frac{1}{\sqrt[]{2}}(|{ψ^{+}}⟩-|{ψ^{-}}⟩). \\ \end{matrix}\end{cases} \) (22)

Then we insert Equation 22 into Equation 21, by transforming the computational basis into the Bell basis.

\( \begin{matrix}|ψ⟩⊗|{ψ^{+}}⟩ & =\frac{α}{2}(|{ϕ^{+}}⟩+|{ϕ^{-}}⟩)|1⟩+\frac{α}{2}(|{ψ^{+}}⟩+|{ψ^{-}}⟩)|0⟩ \\ & +\frac{β}{2}(|{ψ^{+}}⟩-|{ψ^{-}}⟩)|1⟩+\frac{β}{2}(|{ϕ^{+}}⟩-|{ϕ^{-}}⟩)|0⟩ \\ & =\frac{1}{2}|{ψ^{+}}⟩(α|0⟩+β|1⟩)+\frac{1}{2}|{ψ^{-}}⟩(α|0⟩-β|1⟩) \\ & +\frac{1}{2}|{ϕ^{+}}⟩(α|1⟩+β|0⟩)+\frac{1}{2}|{ϕ^{-}}⟩(α|1⟩-β|0⟩). \\ \end{matrix} \) (23)

In this case, if Alice does a Bell Measurement, she has the same chance to obtain every state of \( |{ϕ^{+}}⟩ \) , \( |{ϕ^{-}}⟩ \) , \( |{ψ^{+}}⟩ \) , \( |{ψ^{-}}⟩ \) . By using suitable unitary operation (see the next subsection), Alice can change these four measurement results to some message which can be sent by classical channels.

\( \begin{matrix} & \frac{1}{2}|01⟩(α|0⟩+β|1⟩)+\frac{1}{2}|11⟩(α|0⟩-β|1⟩) \\ & +\frac{1}{2}|00⟩(α|1⟩+β|0⟩)+\frac{1}{2}|10⟩(α|1⟩-β|0⟩). \\ \end{matrix} \) (24)

Step 3. Unitary operation is carried out by Bob.

Alice sends the result of the Bell measurements to Bob by classical messages. Bob can use this message to determine which of the quantum states is this message corresponds to.

\( \begin{matrix}|00⟩→(α|1⟩+β|0⟩)⇀{σ_{x}}, \\ |10⟩→(α|1⟩-β|0⟩)⇀i{σ_{y}}, \\ |01⟩→(α|0⟩+β|1⟩)⇀I, \\ |11⟩→(α|0⟩-β|1⟩)⇀{σ_{z}}. \\ \end{matrix} \) (25)

By taking this operation, Bob can obtain the message qubit \( α|0⟩+β|1⟩ \) . So we have completed the protocol of quantum teleportation.

3. Controlled Remote Implementation of Operations in Three participants

The main goal in this section is to send the unitary operation \( \begin{matrix}U & =⊗_{j=1}^{N}exp[i{α_{j}}{σ_{{n_{{O_{j}}}}}}] \\ \end{matrix} \) to other participants assisted by the controller.

3.1. Basic configuration

Three participants have a configuration in Figure 3. In this case, they share the tripartite graph state

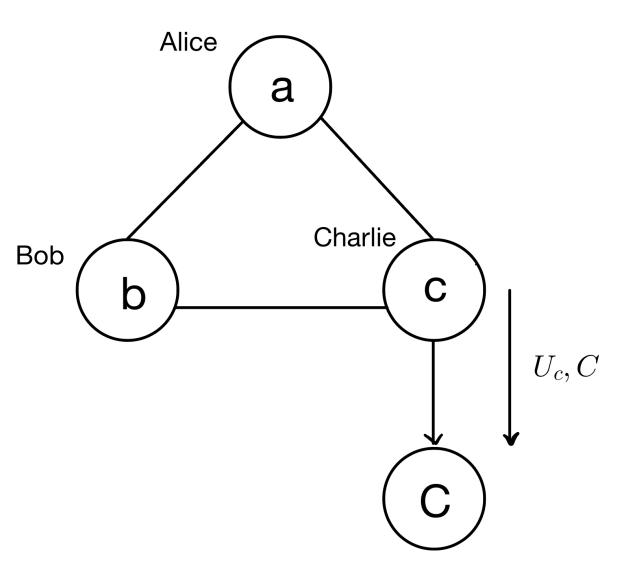
Figure 3. (a) Image content is densely coded (b) for quantum invisible state transfer

\( \begin{matrix}|{h_{3}}⟩ & = C{Z_{(a,b)}}C{Z_{(a,c)}}|+{⟩^{⊗3}} \\ & \begin{matrix}= \frac{1}{2\sqrt[]{2}}{(|000⟩+|001⟩+|010⟩+|011⟩+|100⟩-|101⟩-|110⟩+|111⟩)_{a,b,c}}. \\ \end{matrix} \\ \end{matrix} \) (26)

3.2. Build quantum pair

To accomplish our goal, we implement the unitary operation \( \begin{matrix}{U_{C}} & =exp[iα{σ_{{n_{C}}}}] \\ \end{matrix} \) on system belonging to Charlie

\( \begin{matrix}{U_{c,C}}=|0{⟩_{c}}⟨0|⊗{I_{C}}+{|1⟩|_{c}}⟨1|⊗{σ_{{n_{C}}}}. \\ \end{matrix} \) (27)

By insert Equation 27 to Equation 26 we can get a formula as follows.

\( \begin{matrix}{S_{3}} \prime & = & \frac{1}{2\sqrt[]{2}}(|000{⟩_{a,b,c}}⊗{I_{C}}+|001{⟩_{a,b,c}}⊗{σ_{{n_{C}}}}+|010{⟩_{a,b,c}}⊗{I_{C}}+|011{⟩_{a,b,c}}⊗{σ_{{n_{C}}}} \\ & + & |100{⟩_{a,b,c}}⊗{I_{C}}-|101{⟩_{a,b,c}}⊗{σ_{{n_{C}}}}-|110{⟩_{a,b,c}}⊗{I_{C}}+|111{⟩_{a,b,c}}⊗{σ_{{n_{C}}}}) \\ & = & \frac{1}{2}|+{⟩_{a}}(|00{⟩_{b,c}}⊗{I_{C}}+|11{⟩_{b,c}}⊗{σ_{{n_{C}}}})+\frac{1}{2}|-{⟩_{a}}(|10{⟩_{b,c}}⊗{I_{C}}+|01{⟩_{b,c}}⊗{σ_{{n_{C}}}}). \\ \end{matrix} \) (28)

3.3. Alice measurements

Alice makes measurements. She has the same opportunity to get result \( |+⟩ \) , \( |-⟩ \) . Then Alice informs Bob of the measurement result. If she obtains the result \( |-⟩ \) , then Bob performs the operation \( {σ_{x}} \) on qubit b, otherwise Bob need not perform any operation. They can obtain the stator as follows.

\( \begin{matrix}{S_{3}}″=|00{⟩_{b,c}}⊗{I_{C}}+|11{⟩_{b,c}}⊗{σ_{{n_{C}}}}. \\ \end{matrix} \) (29)

3.4. Charlie measurements

Charlie does measurements, and sends the message to Bob. To predict the result he can get, we need to change Equation 29 to the formula based on \( |+⟩ \) , \( |-⟩ \) .

(30)

By having this state, when Charlie does the measurements, he also has equal opportunity to obtain the result from \( |+⟩ \) , \( |-⟩ \) . Then, he can send the information of result to Bob. If the result is \( |-⟩ \) , then Bob implements the operation \( {σ_{z}} \) on qubit b, otherwise he does nothing. They can obtain the result as follows.

\( \begin{matrix}{S_{3}}=|0{⟩_{b}}⊗{I_{C}}+|1{⟩_{b}}⊗{σ_{{n_{C}}}}. \\ \end{matrix} \) (31)

3.5. Bob measurements and information transmit

Bob implements the operation \( {e^{iα{σ_{{x_{b}}}}}} \) on \( {S_{3}} \) . One can show that, this is equivalent to the effect that Charlie implements the operation \( {e^{iα{σ_{n}}c}} \) on his qubit C.

\( \begin{matrix}|s⟩ & ={e^{iα{σ_{{x_{b}}}}}}{S_{3}}|{Φ_{C}}⟩ \\ & =(|0{⟩_{b}}⊗{I_{C}}+|1{⟩_{b}}⊗{σ_{{n_{C}}}}){e^{iα{σ_{{n_{C}}}}}}|{Φ_{C}}⟩. \\ \end{matrix} \) (32)

In this case, Bob does the projective measurement by \( |0⟩ \) and \( |1⟩ \) . Then he gives the result to Charlile. If the result is \( |1⟩ \) , then Charlie implements the operation \( exp[iπ{σ_{{n_{C}}}}/2] \) on qubit c, otherwise he does nothing. Then he can obtain the operation : \( {e^{iα{σ_{{n_{C}}}}}} \) .

4. Generalized protocol of more parties

In this section, we generalize the protocol in the last section to the case of more parties. We shall implement a global two-qubit unitary gate on two distant parties controlled by different systems. The message is still known by the sender only.

For simplicity we consider four parties, in which Alice is still the judge, Bob is still the sender, and Charlie and Daniel are the receivers, see Figure 4. Suppose the four parties share the four-qubit Greenberger-Horner-Zeilinger (GHZ) state . To realize this state, we need carry out three CNOT gates on parties \( AB \) , \( AC \) and \( AD \) , respectively, see Figure 5. Like the protocol in the last section, Charlie and Daniel respectively perform the controlled unitary gate as follows.

\( {U_{cC}}=|0⟩​⟨0|⊗{I_{2}}+|1⟩​⟨1|⊗{σ_{{n_{1}}}}, \) (33)

\( {V_{dD}}=|0⟩​⟨0|⊗{I_{2}}+|1⟩​⟨1|⊗{σ_{{n_{2}}}} \) ,(34)

where \( C \) and \( D \) are two parties belonging to Charlie and Daniel, respectively. Hence, they can prepare the following stator

(35)

Next, Alice measures her qubit using the basis 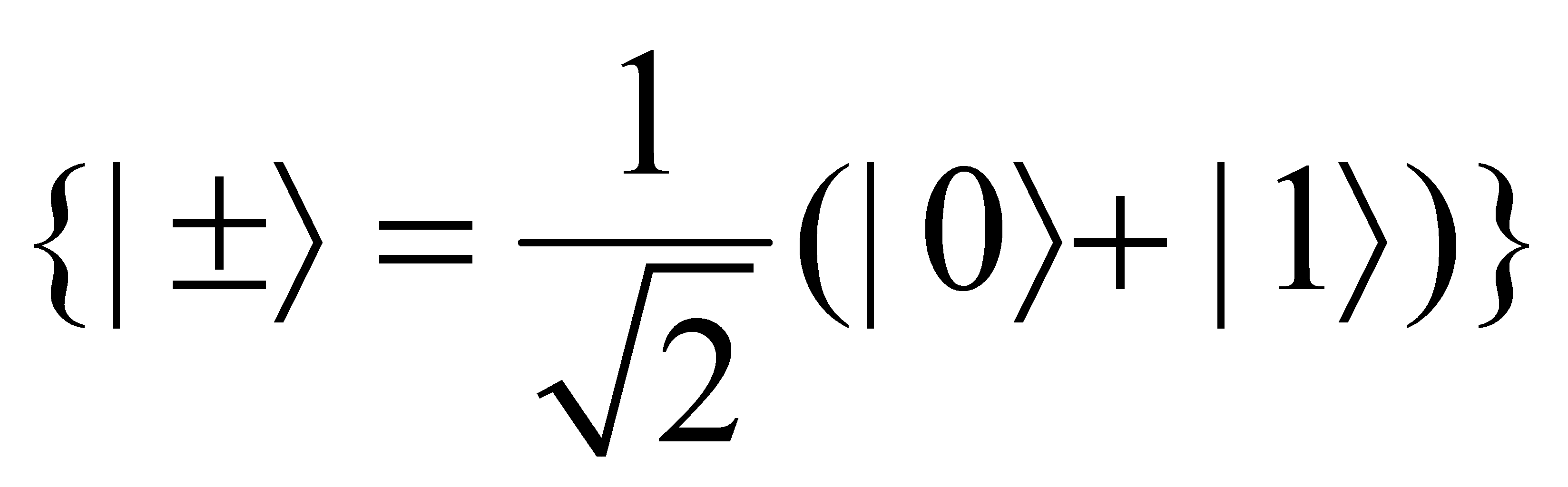of the Pauli gate \( {σ_{x}} \) . Then Alice need notify Bob of the measurement result. If the result is \( |+⟩ \) then Bob does nothing, otherwise Bob performs the Pauli gate \( {σ_{z}} \) . One can see that Bob, Charlie and Daniel are in the following stator of particle \( b,c,d \) , \( C \) and \( D \) .

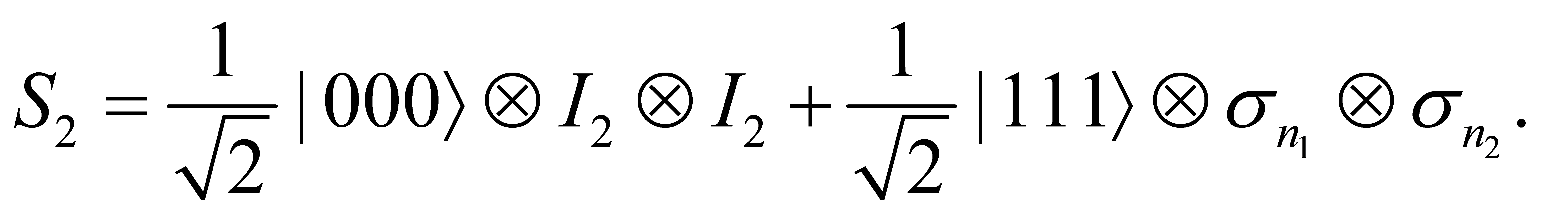(36)

Third, Charlie and Daniel measure respectively particle \( b \) and \( c \) using the basis \( \lbrace |±⟩\rbrace \) . Then they need notify Bob of the measurement result. If the results are both \( + \) or \( - \) , then Bob does nothing. Otherwise, Bob performs the gate \( {σ_{z}} \) . One can see that Bob, Charlie and Daniel are in the following stator of particle \( b \) , \( C \) and \( D \) .

(37)

Fourth, Bob implements the local Pauli gate \( {σ_{{x_{b}}}} \) , and one can show that \( {σ_{{x_{b}}}}{S_{3}}=({σ_{n1}}⊗{σ_{n2}}){S_{3}} \) . Hence we have

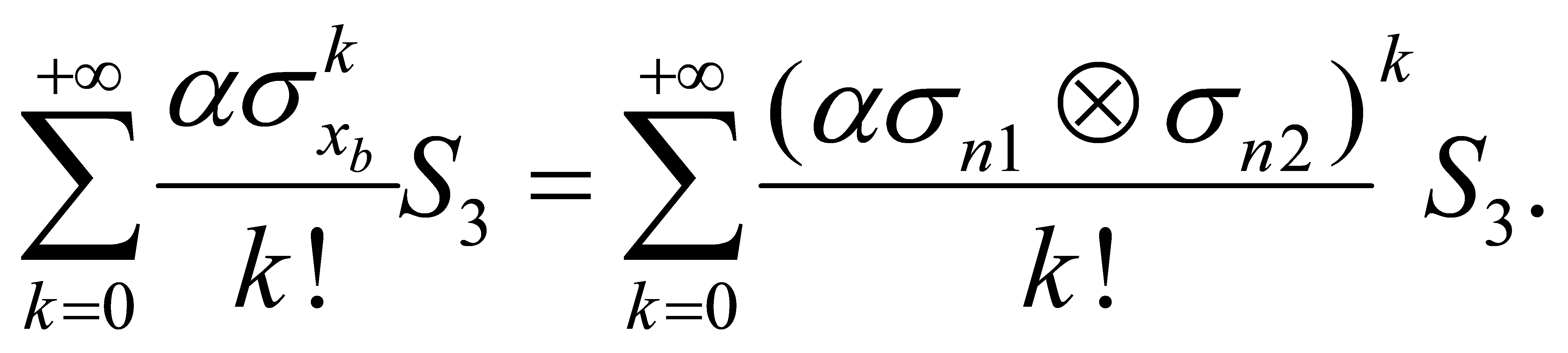(38)

Equivalently we have

\( \begin{matrix}{e^{iα{σ_{{x_{b}}}}}}{S_{3}}={e^{iα({σ_{n1}}⊗{σ_{n2}})}}{S_{3}}={S_{3}}{e^{iα({σ_{n1}}⊗{σ_{n2}})}}. \\ \end{matrix} \) (39)

Finally, Bob measures his qubit using the basis \( |0⟩ \) , \( |1⟩ \) . Then Bob need notify Charlie and Daniel of the measurement result. If the result is \( |0⟩ \) then they do nothing, otherwise they perform the local unitary operation \( {σ_{n1}}⊗{σ_{n2}} \) . As a result, Bob and Charlie have implemented the global unitary gate \( {e^{iα({σ_{n1}}⊗{σ_{n2}})}} \) on their particles \( C \) and \( D \) .

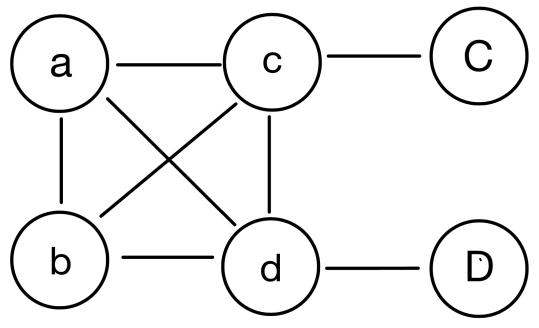
Figure 4. Alice, Bob, Charlie and Daniel respectively possess the particles a,b,c and d. As the judge, Alice measures her qubit, and then the receiver Charlie and Daniel both measure their qubit. As a result, Bob, Charlie and Daniel share a stator of particle b, C and D. Then Bob can perform a local unitary gate containing a parameter unknown to Alice, Charlie and Daniel. It turns out that C and D are performed by a collective unitary gate containing the parameter. So the protocol can transmit classical messages confidentially by quantum means.

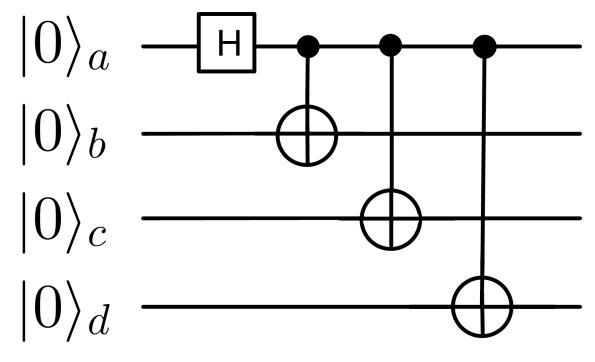
Figure 5. The preparation of four-qubit GHZ state using one Hadamard gate and three CNOT gates.

5. Conclusions

We have shown the protocol of controlled remote implementation of operations in both two and three participants. They show the quantum security guaranteed by the basic rules of quantum mechanics by using entanglement and measurement. An open problem unsolved in this paper is to extend the results to controlled remote implementation of operations of many parties. Whether entanglement in this protocol could be decreased is also an interesting issue for the next step.

Acknowledgments

Authors wishing to acknowledge assistance or encouragement from colleagues, special work by technical staff or financial support from organizations should do so in an unnumbered Acknowledgments section immediately following the last numbered section of the paper.