1. Introduction

Dandelions, scientifically referred to as Taraxacum officinale, have a multifaceted relationship with humans. These perennial herbs have graced our planet for countless years, and they thrive in nearly every temperate zone. Their widespread distribution can be attributed to their unique seed dispersal methods, utilizing the wind and convective updrafts to spread their seeds. While it’s common for most dandelion seeds to fall within a two-square-meter radius, under favourable conditions—such as warmth, dryness, and wind—they can be carried further afield [1].

Nevertheless, the perception of dandelions varies widely among different individuals. To herbalists, these plants are highly valuable due to their rich vitamin and mineral content. Dandelion leaves and roots find their way into teas and various medicinal concoctions. Conversely, for turf managers, dandelions are a major nuisance. Their vibrant yellow color detracts from the visual appeal of lawns, and their tendency to form clumps disrupts the evenness of the turf, creating uneven footing on the field.

Hence, to comprehensively grasp the impact of invasive species like dandelions, it becomes imperative to construct a model that assesses the harm they impose on their environment.

2. Assumptions and Justifications

Assumption 1: To simplify the model, we set a constant fluid medium.

Justification 1: Firstly, the fluid environment in which particle diffusion occurs is approximately homogeneous over the relevant scales. This homogeneity allows us to consider the fluid as a constant medium, simplifying the mathematical formulation of the diffusion model. Secondly, a constant fluid mechanism significantly simplifies the mathematical equations governing particle diffusion. This simplicity facilitates the implementation and numerical simulation of the model, making it computationally more tractable. The use of constant coefficients in the diffusion equation reduces the computational overhead associated with tracking dynamic fluid properties. Thirdly, this assumption is suitable when the temporal and spatial scales of interest are relatively small compared to the characteristic times and lengths associated with significant changes in the fluid environment. This allows us to capture the essential dynamics of particle diffusion without the need to model intricate variations in fluid properties. Fourthly, the primary focus of our model is on the diffusion process itself rather than the detailed dynamics of the fluid. Assuming a constant fluid mechanism aligns with this focus and enables us to isolate the effects of diffusion while avoiding unnecessary complexity related to fluid behavior [2].

Assumption 2: The volume and size of dandelion seeds are not taken into consideration.

Justification 2: Studies consistently indicate that there exists a direct correlation between seed size and the extent of distribution in ecosystems. Specifically, research findings highlight that smaller seeds tend to result in a more expansive distribution area. However, for the sake of model simplification and computational efficiency, we opt to overlook the intricacies associated with seed size variations. Instead, in our modeling approach, we streamline the analysis by adopting an average seed size, thereby facilitating a more straightforward representation of the system. This pragmatic decision allows us to focus on other pertinent factors influencing distribution dynamics, promoting a balance between accuracy and computational manageability in our research framework.

Assumption 3: There are no collisions between particles.

Justification 3: In scenarios where seeds encounter collisions, there exists the potential for these seeds to undergo damage, rendering them incapable of successful dispersal. The intricacy of this phenomenon lies in the uncertainty surrounding the frequency of seed collisions, a variable that could significantly complicate our modeling endeavors. Given the inherent complexity and the lack of precise data on collision frequencies, we have made a deliberate choice to omit the consideration of such instances from our model. While recognizing the importance of this factor in real-world scenarios, the decision to exclude it aims to strike a pragmatic balance, allowing us to maintain a manageable and streamlined model that captures the essence of seed dispersal dynamics without being overwhelmed by the intricacies of collision-related variables [3].

3. Continuous Diffusion Model

3.1. Particle Diffusion Equation

This paper model the distribution of a single dandelion seed, and how it varies over time. By considering the density of the seed at location r and time, we reference the particle diffusion equation (or heat equation), and obtain a one-dimensional diffusion equation,

\( \frac{∂ϕ}{∂t}=D\frac{{∂^{2}}ϕ}{∂{x^{2}}} \) (1)

where \( ϕ(\vec{r},t) \) is a function represents the density of the diffusing material at location \( r \) and time \( t \) , and \( D \) is the diffusion factor.

In this model, \( D \) is constant. We rewrite the linear equation using a vector differential del \( ∇ \) , which

represents the gradient of \( ϕ(\vec{r},t) \) :

\( \frac{∂ϕ(\vec{r},t)}{∂t}=D\cdot {∇^{2}}ϕ(\vec{r},t) \) (2)

However, the particle is moving in a three-dimensional space, we have to derive an equation for three-dimensional diffusion.

To derive the three-dimensional diffusion equation, we start with the one-dimensional diffusion equation:

\( \frac{∂ϕ}{∂t}=D\frac{{∂^{2}}ϕ}{∂{x^{2}}} \) (3)

This equation can be extended to three dimensions by adding two more terms, one for each additional dimension:

\( \frac{∂ϕ}{∂t}=D(\frac{{∂^{2}}ϕ}{∂{x^{2}}}+\frac{{∂^{2}}ϕ}{∂{y^{2}}}+\frac{{∂^{2}}ϕ}{∂{z^{2}}}) \) (4)

This is the three-dimensional diffusion equation. We can also write it in vector form:

\( \frac{∂ϕ}{∂t}=D\cdot {∇^{2}}ϕ \) (5)

\( {∇^{2}}=\frac{{∂^{2}}}{∂{x^{2}}}+\frac{{∂^{2}}}{∂{y^{2}}}+\frac{{∂^{2}}}{∂{z^{2}}} \) (6)

The goal is to find the vector differential del, then evaluate the numerical solution of the distribution with different diffusion factors and time.

3.2. Longitudinal Spatial Distribution of Dandelion Seeds in Unstable Wind Dynamics

Here, to model the diffusion of dandelion seeds across different time points including 1 month, 2 months, 3 months, 6 months and 12 months, hyperparameter space was established. According to the figure below, we saw there was no obvious longitudinal difference since the wind condition is unstable.

Figure 1. Spatial distribution of dandelion seeds across different time points (1 month, 2 months, 3 months, 6 months, and 12 months) when the air dynamic is unstable [4].

3.3. Spatial Distribution of Dandelion Seeds in Different Wind Dynamic Conditions

Here, to consider the model performance in different wind conditions, we simulated a couple of situations as a confounding factor where the wind is (a) very unstable, (b) moderately unstable, (c) slightly unstable, (d) neutral, (e) moderately stable, and (f) very stable shown in figure 2.

Figure 2. Spatial distribution of dandelion seeds in different wind dynamical conditions [5].

Here are the detailed conditions (A) very unstable, (B) moderately unstable, (C) slightly unstable, (D) neutral, (E) moderately stable, and (F) very stable.

3.4. Spatial Distribution of Dandelion Seeds in Different Humidity

Here, to consider the model performance in different humidity values, we simulated the particle distribution when humidity is equal to 1, 10, and 100 when the wind condition is very unstable and very stable respectively shown in figure 3.

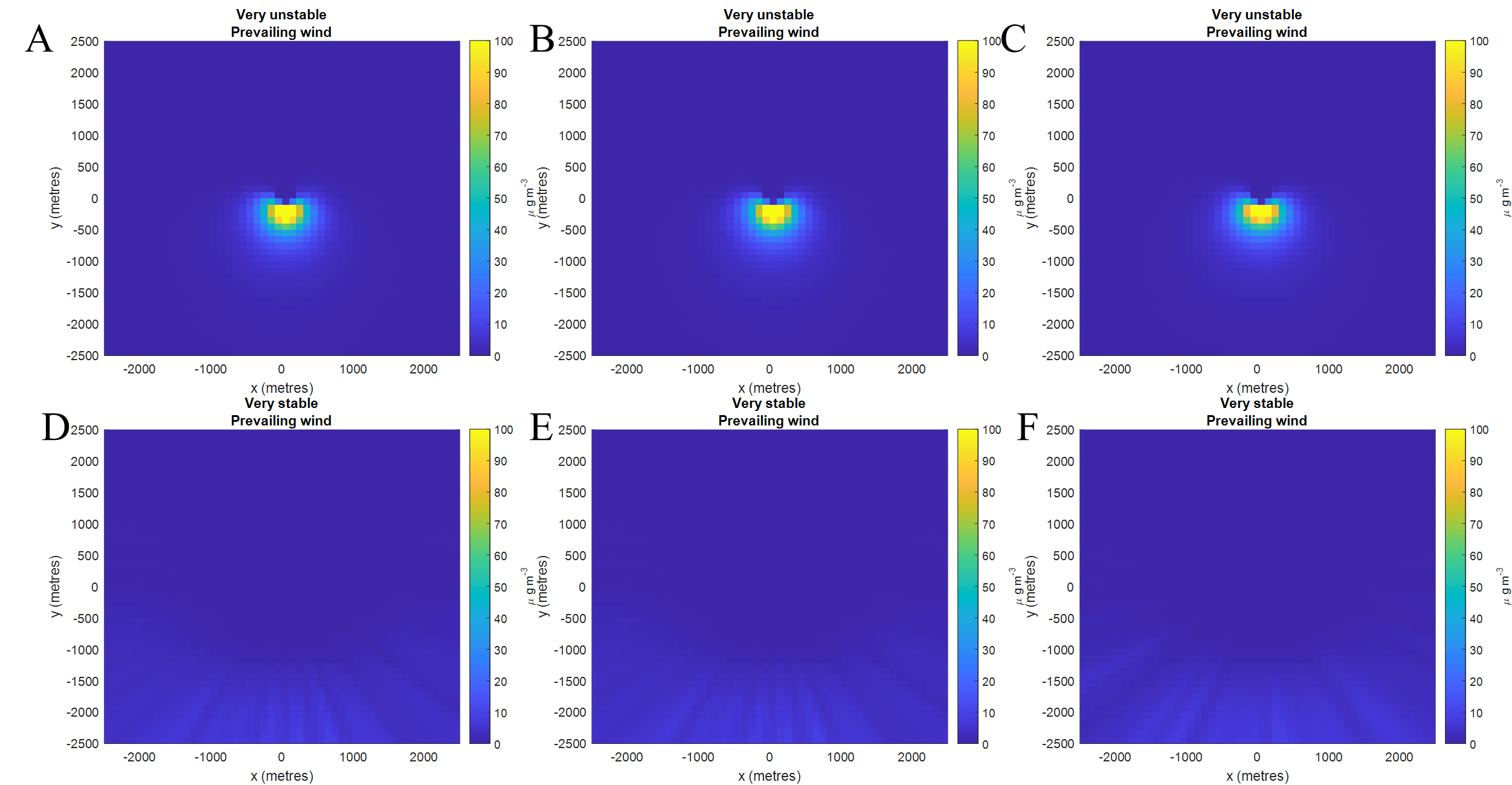
Figure 3. Spatial distribution of dandelion seeds in different humid conditions [6]. (A-C) very unstable wind conditions with humidity values of 1, 10, and 100 respectively; (D-F) very stable wind conditions with humidity values of 1, 10, and 100 respectively.

3.5. Spatial Distribution of Dandelion Seeds in Different Wind Speeds

Here, to consider the model performance in different wind speeds, we simulated the particle distribution when the wind speed is equal to 1m/s, 2m/s, 4m/s, 8m/s, 16m/s, and 32m/s, respectively.

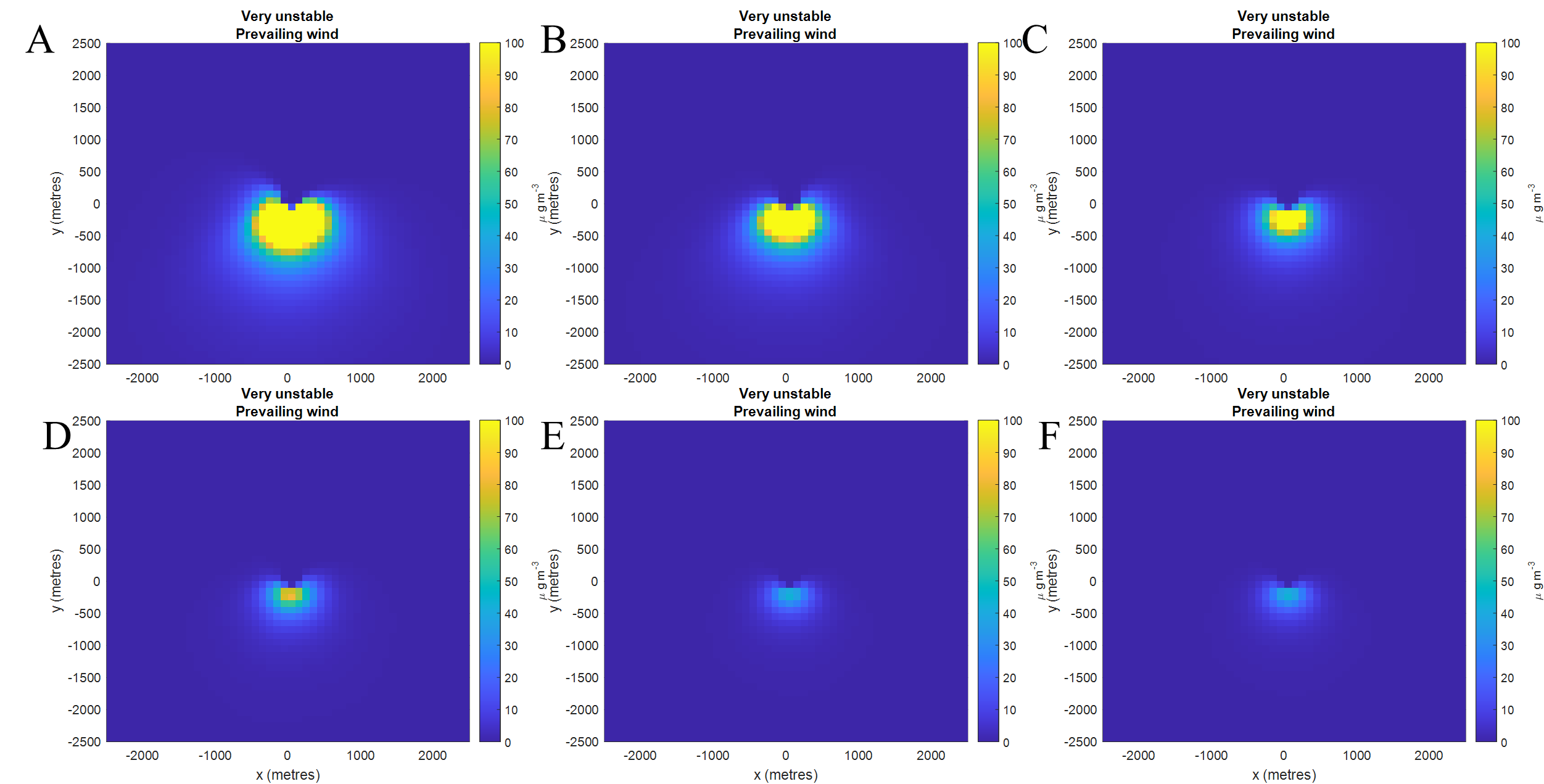
Figure 4. Spatial distribution of dandelion seeds under different wind speeds. (A) 1m/s; (B) 2m/s; (C) 4m/s; (D) 8m/s; (E) 16m/s; (F) 32 m/s [7].

4. Discrete Diffusion Model

The model is first established in one dimension. We assume that particles are moving along a segment following Brownian motion. This means that the particles are distributed following a Gaussian distribution, so they are undergoing continuous-time random walks. We discretize the time domain.

\( \frac{d{P_{n}}(t)}{dt}=\frac{1}{2}({P_{n-1}}(t)+{P_{n+1}}(t))-{P_{n}}(t) \) (7)

Modeling the propagation of 3D dandelion seeds using a 3D random walk involves simulating the stochastic movement of individual seeds within a three-dimensional space. Dandelion seeds are characterized by their aerodynamic structures, designed for wind dispersal. A 3D random walk is a mathematical approach that mimics the random and unpredictable nature of seed movement in the air.

To initiate the modeling process, the 3D space needs to be discretized into a grid or mesh, forming a lattice structure. Each lattice point represents a possible position of a dandelion seed within the 3D environment. At the beginning of the simulation, the seeds are distributed across the lattice, typically starting from a central location or a predefined source point. The random walk is then executed iteratively for each seed.

During each iteration, a seed randomly selects one of the neighboring lattice points as its next position. This randomness accounts for the chaotic nature of wind-driven seed dispersal. The direction and distance of the seed’s movement are determined based on a random process, often modeled using statistical distributions. For example, a Gaussian distribution might be employed to simulate the varying wind forces that influence seed displacement.

To incorporate realism into the model, factors such as air resistance, turbulence, and gravitational effects can be considered. These factors can be incorporated into the random walk algorithm to influence the seeds’ movement patterns. Additionally, the model may account for the interaction between seeds, simulating scenarios where seeds influence each other’s trajectories through local interactions.

The simulation continues for a specified number of iterations or until certain criteria are met, such as a predefined distance traveled by the seeds. The resulting output provides insights into the spatial distribution of dandelion seeds over time, offering a visual representation of their dispersal patterns in a 3D space.

It’s important to note that the accuracy of the model depends on the fidelity of the chosen random walk algorithm and the incorporation of relevant environmental factors. Calibration and validation against empirical data can help refine the model parameters to better reflect real-world scenarios. This 3D random walk approach provides a flexible and computationally efficient method for studying the intricate dynamics of dandelion seed propagation in diverse environmental conditions.

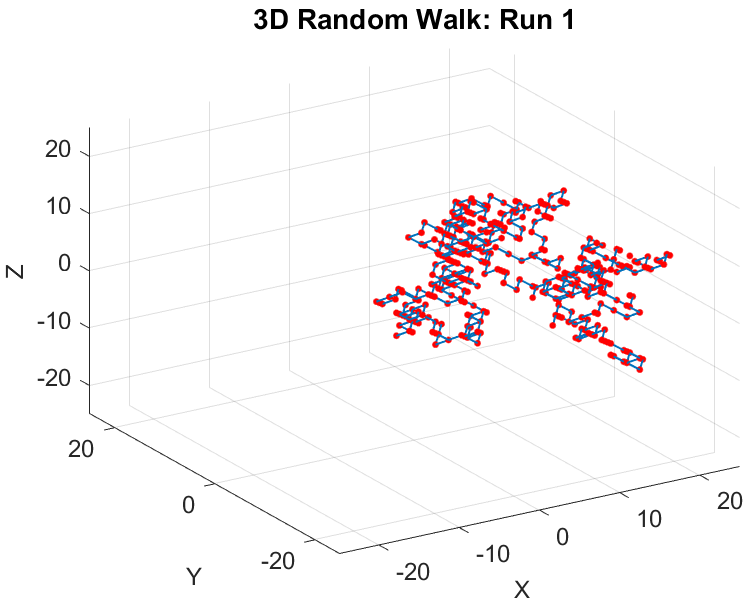
Figure 5. 3D simple random walk [8].

5. Interspecies Competition Model

5.1. Species

There are two species A and B. When they live alone, their numbers change following the logistic change.

\( \frac{dx}{dt}={r_{1}}\cdot x(1-\frac{x}{{n_{1}}}) \) (8)

\( \frac{dy}{dt}={r_{2}}\cdot y(1-\frac{y}{{n_{2}}}) \) (9)

When the two species live together, the competitive effect of B on the growth of A is proportional to the number of B. A has the same effect on B. So we can get these formulas:

\( \frac{dx}{dt}={r_{1}}\cdot x(1-\frac{x}{{n_{1}}}-{s_{1}}\frac{y}{{n_{2}}}) \) (10)

\( \frac{dy}{dt}={r_{2}}\cdot y(1-\frac{y}{{n_{2}}}-{s_{2}}\frac{x}{{n_{1}}}) \) (11)

Where \( x(t) \) and \( y(t) \) are the numbers of populations A and B, respectively, \( {r_{1}} \) and \( {r_{2}} \) are their inherent growth rates, and \( {n_{1}} \) and \( {n_{2}} \) are their maximum capacities. The meaning of \( {s_{1}} \) is that for the resources to support A, the consumption per unit quantity of B (relative to \( {n_{2}} \) ) is \( {s_{1}} \) times the consumption per unit quantity of a (relative to \( {n_{1}} \) ), and the same is true for \( {s_{2}} \) .

5.2. Impacts of Interspecies Competition

The graph (Figure 6.) indeed shows that the population of dandelions, represented by the red line, increases over time, while the population of other species, represented by the blue line, decreases. However, the blue line does not drop to zero, indicating that the other species are not becoming extinct due to the presence of dandelions [10]. This suggests that while dandelions may compete with other species for resources, they do not completely dominate these resources and cause other species to become extinct.

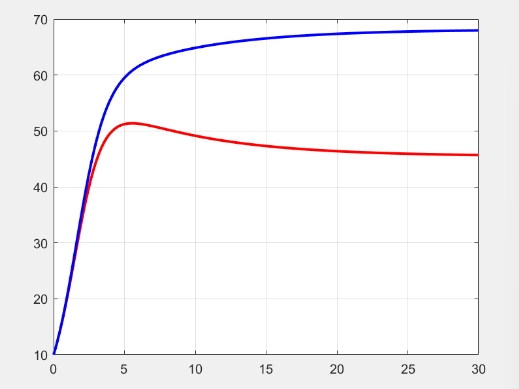
Figure 6. Interspecies competition model with two species [9]

The term “invasive species” is often used to describe a species that is non-native to a specific location and has a tendency to spread, which can cause damage to the environment, the economy, or human health. Dandelions are considered invasive in some regions such as North America and parts of Asia. However, it’s important to note that not all non-native species are invasive. For a species to be considered invasive, it must cause harm in its new environment.

In the case of dandelions, they can compete with native plants for resources and take over lawns and gardens. However, they also provide benefits such as being an excellent source of nectar and pollen for bees, butterflies, and other pollinators. Therefore, whether dandelions are viewed as a nuisance or a blessing can depend on the specific context and perspective.

In conclusion, while dandelions can spread and compete with other species for resources, the fact that they do not cause other species to become extinct, as shown in your graph, suggests that they do not exhibit the level of harm typically associated with invasive species. Therefore, it could be argued that dandelions should not be classified as an invasive species based on this criterion. However, whether a species is considered invasive can depend on various factors and may vary by region.

6. Conclusion

This paper formulates a simplified equation within the Continuous Diffusion Model, enabling us to predict the distribution of a seed at any given location and time based solely on its density. This streamlined approach facilitates easy implementation and accelerates the evaluation process.

Our model’s practicality stems from its consideration of the three-dimensional nature of the real world. We extrapolate a three-dimensional equation from a one-dimensional counterpart, capturing the unpredictable aspects of seed movement. This 3D random walk incorporates factors such as air resistance, turbulence, gravitational effects, and more.

The accuracy of our model relies on the fidelity of the chosen random walk algorithm and the thorough incorporation of relevant environmental factors.

In reality, the uneven distribution of the fluid medium introduces irregularities in the spread of dandelion seeds, challenging the regularity and predictability of their dispersion.

Our model overlooks the impact of seed size, a crucial variable that influences distribution area. Specifically, smaller seeds tend to cover a larger area. Currently, we use the average size of dandelion seeds in our model, neglecting the variations in size that exist in reality.