1. Introduction

The primary issue to solve is the relationship existing between the number of Hamiltonian cycles, labeled as \( {\ \ \ _{H}} \) , and generating sets \( S \) of directed Cayley graphs \( DiCay(G:S) \) (Tripi[2]) of a Group \( G \) . Motivated by the conjecture that there is a hamiltonian circuit in every Cayley digraph on a dihedral group (Holsztyński and Strube[3]), we demonstrated that if \( S=r \) and \( s \) , the directed Cayley graph of Dihedral groups \( {D_{2n}} \) will consist of \( n \) Hamiltonian cycles. In addition, we provided evidence indicating that \( {\ \ \ _{H}}(DiCay({D_{2n}}:S))=2 \) is consistently present with \( S \) under certain conditions. Inspired by Cayley’s Theorem Extended (STELOW[4]), it is our objective to offer a generalization of the principles found in Dihedral groups to Symmetric groups. For Symmetry groups of Platonic solids and Symmetric groups, we encountered difficulty in deriving a general rule. Nevertheless, based on graphical evidence, we came up with some conjectures. This paper is organized by treating each of the cases in order, starting with Dihedral groups, followed by Symmetry groups of Platonic solids and Symmetric groups.

2. Dihedral Groups

THEOREM 2.1: If the generating set of \( DiCay({D_{2n}}:S) \) is in the form of \( {r^{i}} \) and \( s{r^{j}} \) with \( r \) and \( s \) as the preliminary elements, where \( 0≤i≤n-1 \) , \( 0≤j≤n-1 \) , then there exists at least one Hamiltonian cycle in this graph.

Proof: Given the fundamental symmetries, specifically \( r \) and \( s \) , within the Dihedral groups, it follows that \( {D_{2n}} \) can be expressed as the set \( e,r,{r^{2}},...,{r^{n-1}},s,sr,s{r^{2}},...,s{r^{n-1}} \) with each element corresponding to a composition of these symmetries. In the directed Cayley graph representation of \( {D_{2n}} \) with the generating set of \( r \) and \( s \) , \( r \) will form 2 distinct cycles of length \( n \) , and \( s \) segregate the elements into pairs with \( \frac{n}{2} \) elements in each pair. The bidirectional edge connects the two vertices in each pair. Considering that \( DiCay({D_{2n}}:r,s) \) possesses a minimum of one Hamiltonian cycle, it can be inferred that more elements in the generating sets will always form at least one Hamiltonian cycle in the graph.

EXAMPLE 2.2: A concrete example is provided by Figure 1:

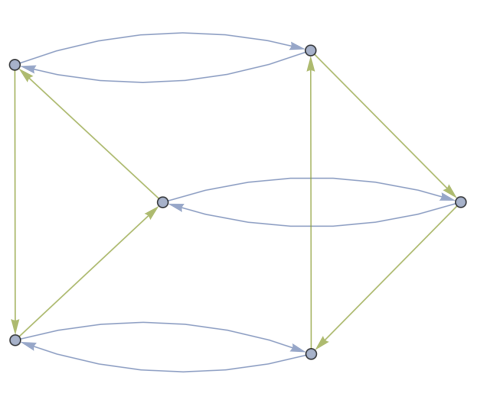
Figure 1. The directed Cayley graph of \( {D_{6}} \) with the generating set of \( r \) and \( s \) .

THEOREM 2.3: The number of Hamiltonian cycles of the directed Cayley graph of Dihedral groups with the generating set of \( r \) and \( s \) is n. i.e.:

\( {\ \ \ _{H}}(DiCay({D_{2n}}:r,s)) = n \ \ \ (1) \)

Proof: In a geometric approach, we can establish the proof for this theorem. Let us consider the \( DiCay({D_{2n}}:r,s) \) structure. As illustrated in Figure 2, when the generator \( r \) is applied, it forms an \( n-gon \) . Additionally, by multiplying each vertex in the \( n-gon \) with \( s \) , we can extend it to include \( n \) bidirectional edges. Consequently, the \( DiCay({D_{2n}}:r,s) \) structure consists of both an inner and an outer \( n-gon \) . To identify the Hamiltonian cycles within this structure, we can initiate our journey from the identity element and traverse through the inner \( n-gon \) until we reach the vertex \( {r_{n-1}} \) . From there, we move to the outer \( n-gon \) using one of the bidirectional edges and proceed in the opposite direction along the \( n-gon \) . Eventually, we arrive at the vertex \( s \) . Only one edge permits us to return to the identity element. Moreover, the Cayley graph possesses symmetry through a rotation of \( \frac{2π}{n} \) , thereby ensuring the existence of precisely \( n \) Hamiltonian cycles in Figure 2:

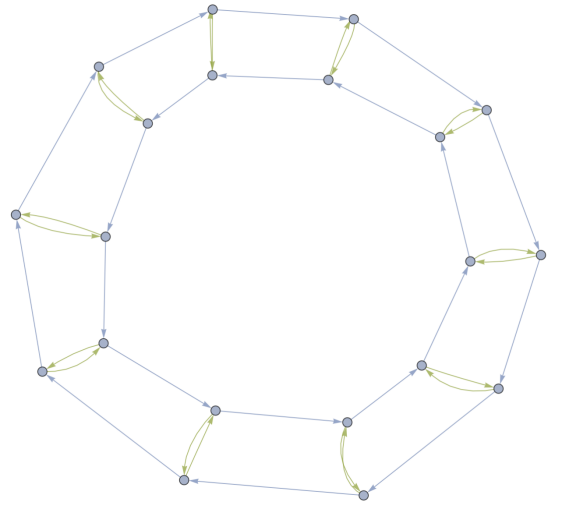
Figure 2. The directed Cayley graph of \( {D_{2n}} \) with the generating set of \( r \) and \( s \)

EXAMPLE 2.4: According to the observations illustrated in Figure 3, it is evident that by adhering to the procedures outlined in the proof, the initial vertex can be chosen from among \( e \) , \( r \) , \( {r^{2}} \) , and \( {r^{3}} \) . This leads to the conclusion that the existence of four Hamiltonian cycles is guaranteed.

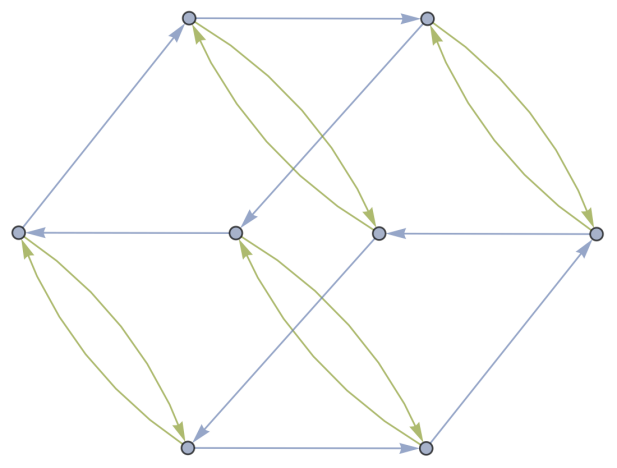
Figure 3. The directed Cayley graph of \( {D_{8}} \) with the generating set of \( r \) and \( s \)

THEOREM 2.5: In directed Cayley graphs of Dihedral groups generated by the elements \( s{r^{i}} \) and \( s{r^{j}} \) , where \( 0≤i≤n-1 \) , \( 0≤j≤n-1 \) , and \( i≠j \) , the situation where

\( {\ \ \ _{H}}(DiCay({D_{2n}}:s{r^{i}},s{r^{j}}))=2 \ \ \ (2) \)

Proof: Given the generating elements \( s{r^{i}} \) and \( s{r^{j}} \) , it is evident that each element will produce \( \frac{n}{2} \) pairs of bidirectional edges that link two vertices. By Induction:

Base Case: \( {\ \ \ _{H}}(DiCay({D_{6}}:s,sr))=2 \)

Suppose \( {\ \ \ _{H}}(DiCay({D_{2n}}:s{r^{i}},s{r^{j}}))=2 \) :

By performing a left multiplication of \( s{r^{i}} \) and \( s{r^{j}} \) , the vertices on the Cayley graphs are transformed into \( e,s{r^{i}},{s^{2}}{r^{i-j}},{s^{3}}{r^{2i-j}}...,{s^{2n}}{r^{n(i-j)}} \) .

The equation \( {s^{2n}}{r^{n(i-j)}}=e \) implies that the vertices form a closed cycle connected by bidirectional edges. In \( (DiCay({D_{2(n+1)}}:s{r^{i}},s{r^{j}})) \) , the vertices are interconnected in the same manner as in \( (DiCay({D_{2}}n:s{r^{i}},s{r^{j}})) \) . The final vertex is denoted as \( {s^{2n+2}}{r^{(n+1)(i-j)}} \) .

It is required to demonstrate that

\( {s^{2n+2}}{r^{(n+1)(i-j)}}=e \ \ \ (3) \)

and,

\( {s^{2n+2}}={s^{2(n+1)}}=e \ \ \ (4) \)

Since \( {r^{n+1}}=e \) in \( (DiCay({D_{2(n+1)}}:s{r^{i}},s{r^{j}})) \) , it follows that \( {r^{(n+1)(i-j)}}=e \) .

Therefore, \( {s^{2n+2}}{r^{(n+1)(i-j)}}=e \) .

\( {\ \ \ _{H}}(DiCay({D_{2n+2}}:s{r^{i}},s{r^{j}}))=2 \) .

EXAMPLE 2.6: A prominent instance can be observed in Figure 4, which has 2 Hamiltonian cycles.

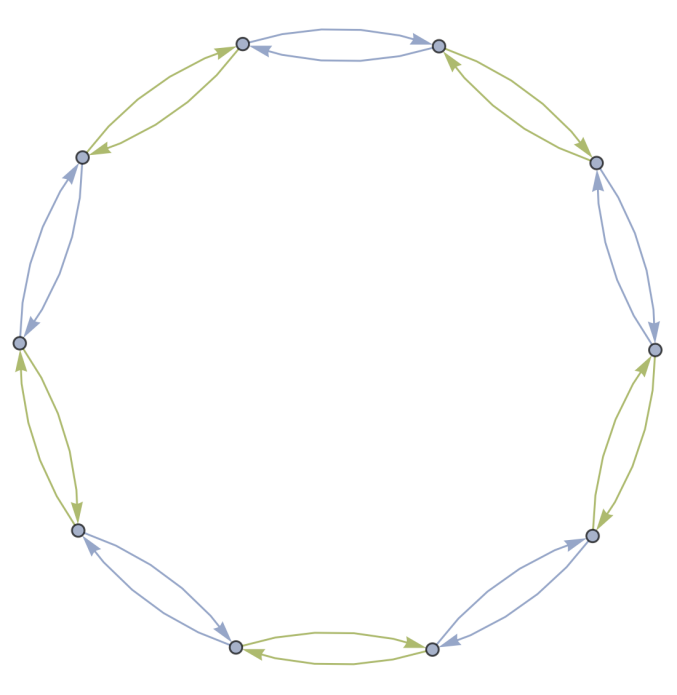
Figure 4. The directed Cayley graph of \( {D_{10}} \) with the generating set of \( (14)(23) \) and \( (12)(35) \)

3. Platonic Solids and Symmetric Groups

CONJECTURE 3.1: There are no Hamiltonian cycles in the directed Cayley graph of the Symmetry group of Platonic solids with the generating set r, s.

EXAMPLE 3.2: In the case of the Tetrahedral group T, which possesses 12 elements, \( {\ \ \ _{H}}(DiCay(T:(123),(12)(34))=0 \) . As the quantity of elements escalates, it becomes increasingly challenging to procure a Hamiltonian cycle. As it is shown in Figure 5:

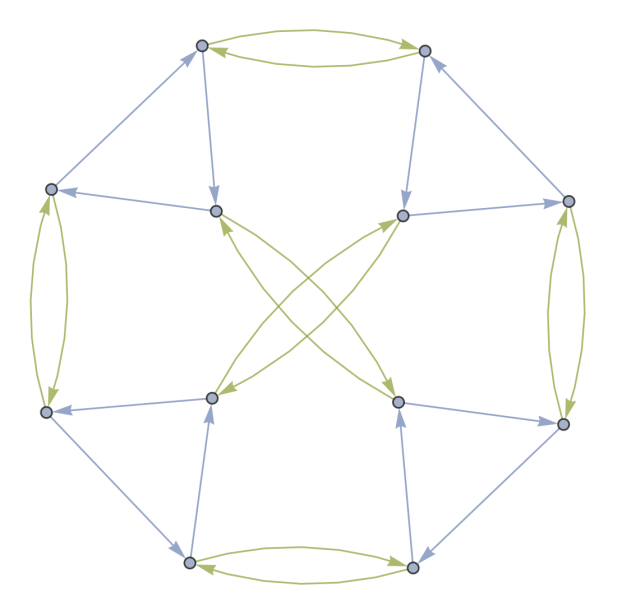
Figure 5. The directed Cayley graph of the Tetrahedral group \( T \) with the generating set of \( (123) \) and \( (12)(34) \)

CONJECTURE 3.3: In the directed Cayley graph of Symmetric groups, it has been observed that the generating set of \( (12) \) and \( (12...n) \) can solely yield a Hamiltonian cycle when \( n≠4 \) .

EXAMPLE 3.4: As shown in Figure 6, there exist Hamiltonian cycles.

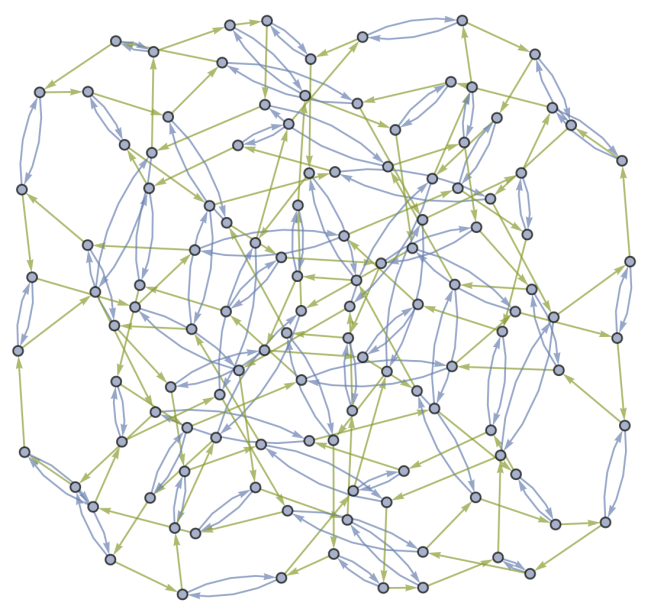
Figure 6. The directed Cayley graph of \( {S_{5}} \) with the generating set of \( (12) \) and \( (12345) \)

4. Final Remarks

In previous researches on Hamiltonian cycles, A. Heus and D. Gijswijt [5] proved that there exists at least one Hamiltonian cycle in the directed Cayley graph of Symmetric groups if the generating set includes only transpositions.

5. Conclusion

In the first section of this work, we initiated our study by considering the existence of Hamiltonian cycles in Dihedral groups. We proved that the directed Cayley graph of a Dihedral group will have at least one Hamiltonian cycle if the generating sets is in the form of \( {r^{i}} \) and \( s{r^{j}} \) with \( r \) and \( s \) as the preliminary elements. Additionally, we proved \( {\ \ \ _{H}} \) \( (DiCay({D_{2n}}:r,s)) \) = \( n \) , which is a generalization in Dihedral groups. Subsequently, we proceeded to explore the specific case in which the generating set of the directed Cayley graphs of Dihedral groups is in the form of \( s{r^{i}} \) and \( s{r^{j}} \) and prove that \( {\ \ \ _{H}}(DiCay({D_{2n}}:s{r^{i}},s{r^{j}}))=2 \) always exists. In the other section, we proposed conjectures regarding the existence of Hamiltonian cycles in Symmetry groups of Platonic solids and Symmetric groups.

Drawing upon the theorems presented in this paper, it is hopeful that this finding will contribute to addressing further problems regarding the relationship between the number of Hamiltonian cycles and generating sets in the general Symmetric groups.