1. Introduction

The randomized algorithm generally refers to employing randomness to create different possible solutions. Examples of such algorithms used in video games include dice rolling, occasional critical hits, random generation of Non-Player Characters (NPCs), and procedural generation of infinite game maps.

With the continuous transformation and improvement of technologies, how to make a video game replayable without being mundane becomes a huge challenge for designers. As great efforts are being put into randomized algorithms, it is gradually mastered by programmers, and the issue is now being solved. However, the specific details and importance of the randomized algorithm are still rarely known by people.

2. Background

2.1. Pseudo-Random Number Generator (PRNG)

To talk about randomness in video games, a very common misconception is that a randomized algorithm does not mean that the numbers it generates are truly random. Since computers are unable to generate so-called “true random numbers”, all the randomness in video games is pseudo-randomness. In fact, programmers could use pseudo-random number generator (PRNG) to create numbers that look “random”, which are actually not. This means as long as the given set of random bits called the seed does not change, no matter how many times the generator is run, the results —— the numbers are the same and fixed [1].

Most game engines like Unity and Unreal provide simple random functions that directly produce randomized numbers. The principles of these random functions are quite rough.

Another example of PRNG is the random module in Python’s standard library. With the function random.seed(), programmers could enter an integer as the parameter into the bracket. It would initialize the PRNG and the generator would form a fixed seed based on the value it has received from the user.

The random values generated each time from the PRNG algorithm are the same, as a result of the same seed value. This is what we call as a “pseudo-random number”. It looks random, but actually, it is controlled by the seed entered. To avoid this, the most common way is to use the system time as the random seed.

Nevertheless, these basic random numbers are obviously high-uniform and unsuitable to use in all relevant applications of randomness. Game players are likely to feel mad if the generator makes the character in the game make numerous continuous non-critical attacks with a high critical probability. Game designers need to make efforts to make the randomness in the game more relatively random, resulting in better players’ experiences. Therefore, they use advanced algorithms based on these random numbers or randomized algorithms.

2.2. Randomized Algorithm

A randomized algorithm is an algorithm that incorporates an element of chance as a fundamental aspect of its procedure or logic based on the premise of generating uniform random numbers through specific random functions. The algorithm typically employs uniformly random numbers as an auxiliary input to ascertain its behavior, aiming to achieve commendable performance in an “average case” across all potential scenarios determined by the uniform random numbers, thus enabling players to experience enhanced comfort during gameplay. In essence, a random function serves as an integral component of a randomized algorithm [2-4].

2.3. Procedural Content Generation (PCG)

According to Josh Bycer [5], procedural content generation (PCG) means that the game itself creates original content for the player to explore or play. The computer could generate data by itself and could complete the entire design of the game by itself without the source code or any help from the programmers. In this way, the computer would continuously improve the content it generates, similar to the self-learning process of Artificial Intelligence.

PCG is actually different from random generation, although these two words seemingly have a close relationship and are used together in our daily lives. In terms of terminology, random generation simply refers to generating data randomly based on predefined rules and instructions. In other words, when using random generation, the programmers have already told the computer what it should do, and the computer only needs to shuffle the order and rearrange the data with its own logic to make these data look logical and reasonable [5,6].

3. Illustration of Common Randomized Algorithms

Randomized Algorithm is one of the most complicated algorithms, which is composed of many small branches. This section discusses the mathematical principles of different types of randomized algorithms and the differences between each of them.

3.1. Gaussian Randomness

Gaussian distribution, also known as the normal distribution, a vital class of continuous probability distributions for real-valued random variables, means when viewing statistics, the attributes or values being measured are likely to be distributed in the condition that most cases only distribute in the center of the whole part, but a tiny number of cases would distribute in a much larger range of values (see Fig. 1). Moreover, the majority of the values fall within the realm of the average range, with only a handful of values lying beyond this average threshold, either surpassing it or falling short of it [2,3,7]. To generate Gaussian randomness, if we take three uniform random numbers, which are generated by the rand() function for example, and calculate the sum of them, we can receive random numbers with such normal distribution.

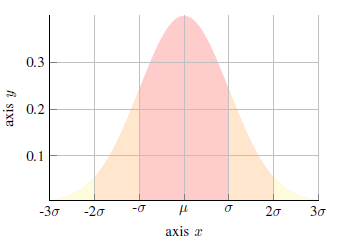
Figure 1. Normal Distribution

Moreover, the central limit theorem describes that the sum of uniform random numbers in such a range would approach a normal distribution with a standard deviation of √σ ÷ 3 and a mean of µ. S is how many numbers are added. If we choose S to be 3, and the standard deviation would be 1, and we would nearly get a standard Gaussian distribution as a result. The code in Unity shows how simple it is to create Gaussian randomness below [2].

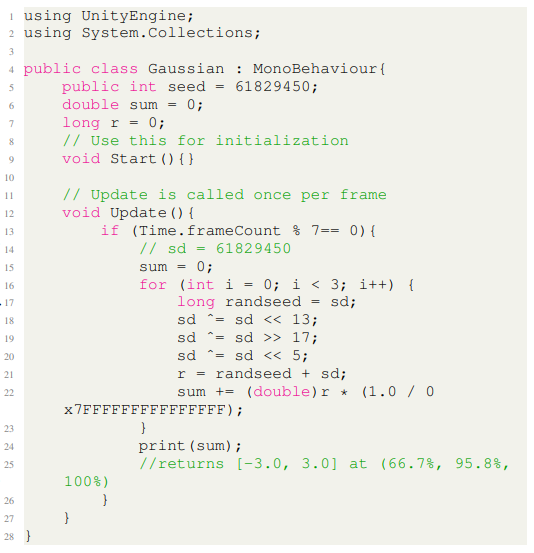
In the aforementioned code, the homogeneous arbitrary numbers are generated employing the pseudo-random number generator. The program yields figures encompassed within the interval of [-3.0, 3.0], with an absolute certainty of 100% for those falling within three standard deviations. Furthermore, 95.8% of the values lie within two standard deviations, while 66.7% reside within one standard deviation. The code at hand sufficiently generates Gaussian randomness for games. However, it is imperative to elucidate a number of concealed distinctions. A genuine Gaussian distribution would produce values that transcend both extremities and exist amidst the range of [–3, 3]. In light of this, Marsaglia and Bray offer a methodology (an enhanced approach derived from the Box–Muller transform). The C++ code for this improved method is presented below [8].

With this method, A normal random variable X may be generated in terms of uniform random variables U1, U2, in the following simple way: 86% of the time, put X=2(U1+U2+U3−1.5), 11% of the time, put X=1.5(U1+U2−1), and the remaining 3% of the time, use a more complex procedure so that the resulting mixture is correct. This method takes only half as long as the very fastest methods, requires very little storage space, and is much simpler [9].

3.2. Filtered Randomness

Sometimes, the unpredictability of randomness can appear excessively haphazard (especially in the context of video games). In numerous instances, when employing consistent randomness, the outcome may deceptively materialize as non-random or inequitable to players in the immediate term. When generating a sequence of arbitrary values, whether binary or derived from a specific numerical range (whether integers or floating point numbers), or even if these values correspond to visual effects rather than straightforward numerical quantities, there are often occurrences where an abundance of repetitive values or sequences of values may emerge, thus erroneously imparting a sense of non-randomness to the player. Initially, this appears to be an incorrect perspective, but there is ample evidence to suggest that humans tend to perceive small fragments of randomness as being truly random. Perhaps the player thought that what generates the sequence is either manipulated, broken, or tricked - all bad qualities due to randomized methods or AI [10].

In order to enhance the apparent randomness and fairness for players in the short term, an immediate approach would be to devise functions that substitute the previously randomized elements with appropriate ones, thus preventing the discovery of extreme instances or anomalies. It is equally important to tailor these rules for each unique case of randomness, treating each decision in isolation and solely considering its own generated values. Additionally, filtered randomness may be employed when dealing with Gaussian numbers to mitigate an excessive level of randomness if deemed necessary. Consequently, provided below is a selection of pertinent code outlining the rules for filtering randomness [2,3].

Filtering Integer Ranges: This is similar to filtered binary randomness, and rules could be built to percolate exceptions that occur within the range of numbers. The following is a list of pretty radical rules that can be carried out. According to these rules, any breach of the rule would lead to a re-rolling of the value, which is then validated against the rule again.

Rules

•Repeating numbers.

•Repeating numbers separated by one digit.

•4 increasing or decreasing count sequences.

•Too many values at the top or bottom of a range within the last 10 values.

•The case of two numbers in the last 10 values.

•There are too many specific numbers in the last 10 numbers

e.g.

Original sequence:

2231255222257775067756406

1448482102435500989388459

5960788996495778075328157

4605482138446235103745368

Filtered sequence:

2231255222257775067756406

1448482102435500989388459

5960788996495778075328157

4605482138446235103745368

3) Filtering Floating Decimal Ranges: In order to percolate floating decimal numbers in the range [0,1], we must design rules to avoid aggregating all similar numbers and to prevent increasing or decreasing the number of runs. If any of the above rules are breached, we would easily delete the value and request a new randomized value that could pass all the rules.

Rules:

•If 2 consecutive numbers differ by less than 0.02, reroll.

•If 3 consecutive numbers differ by less than 0.1, reroll.

•If there is an increasing or decreasing run of 5 values, reroll.

•If there are too much values at the bottom or top of the whole range within the last 10 values, reroll.

4) Filtering Gaussian Ranges: On account of Gauss numbers are too similar to floating decimal numbers, the same rules would be applied. Nevertheless, people could use the following rules in order to avoid the specific exceptions that are particular to Gaussian numbers.

Rules:

•If there are 4 consecutive numbers that are all below or above 0, reroll.

•If there are 4 consecutive numbers in the 2nd or 3rd deviations, reroll.

•If there are 2 consecutive numbers in the 3rd deviation, reroll.

3.3. Drunkard’s Walk

In mathematics, a stochastic trajectory, known as a random walk, characterizes a journey comprised of a sequence of serendipitous strides within a mathematical domain. Various manifestations of randomness embody variables that subtly and capriciously alter over time, thus embodying the essence of these random walks. These variables may influence atmospheric visibility or cloud formation, the fluctuating value of a commodity, and even the intricate cartography of a labyrinthine dungeon [11,12].

In a video game, especially in PCG, the randomized algorithm used in the code is Drunkard’s Walk. The Drunkard Walk is a certain type of random walk and also a highly randomized tunneling algorithm that is one of the most simple dungeon generation algorithms. Tunneling algorithms dig corridors and rooms out of solid terrain, much as a real dungeon architect might. It gets its name from the staggering patterns it makes. Drunkard’s walk algorithm works by choosing a random point and then moving randomly. This path is repeated until it reaches the desired level [13,14]. In a more detailed explanation, the algorithm is as follows:

1)Pick a random point on a filled grid and mark it empty.

2)Choose a random cardinal direction (N, E, S, W).

3)Move in that direction, and mark it empty unless it already was.

4)Repeat steps 2-3, until you have emptied as many grids as desired.

The code below shows an implementation of Durkward’s Walk in Rust. The function keeps spawning drunkards until there have sufficient map coverage [15].

The Drunkard Walk ensures connectivity from the initial grid selected, and you have the ability to ensure that a certain proportion of the grid has been carved out as well. Unless the grid is extensive, it is advisable to favor the direction chosen towards the center of the grid, as the drunkard walk may potentially encounter the edges in an unnatural manner. Additionally, you may opt to favor the drunkard walk in selecting the last direction it traveled, thus creating lengthier corridors.

3.4. Perlin Noise

Perlin noise is one type of noise maps that is frequently used in game design. Its name came from its developer Ken Perlin, who designed it in 1983. It is very useful to simulate natural qualities such as clouds, landscapes or marble textures (see Fig.2). As a result, it often helps the terrain generation part of a game. Different from filtered generation, Perlin noise aims at making the transition of each piece of data more coherent and smooth [2].

Figure 2. Three examples of Perlin noise in generating different textures [16]

Another possible use of such a smooth nature is to simulate the mood shifting of each NPC. Instead of being from happy to angry abruptly, an NPC that gradually goes from happy to indifferent first then becomes agitated would be more favorable. In under words, adding more details to the elements of a game makes it more natural and amiable for players, and Perlin noise was born for this to come true [3].

But how could a Perlin noise map be generated? The first useful concept is the octave, which is an individual layer of data, that can be further combined with each other to form a complete sequence of values. While generating Perlin noise, the different level of details is controlled by the number of octaves used. The steps to make and use octaves can be summarized in the following points [2]:

1)Choose a range of random numbers.

2)Apply a mathematical function to generate middle signals between discrete data. This process is also known as interpolation. In ideal situation, the S-curve function 6t2 − 15t4 + 10t3 is applied as a result of its abundant mathematical properties.

3)An octave is produced

4)Scale the octave with an amplitude (frequency)

5)Adding it to other octaves, and then a simple 1-dimensional Perlin noise signal could be produced.

This process is also shown in Fig.3., where 5 samples of octave signals are created, to generate a basic noise map.

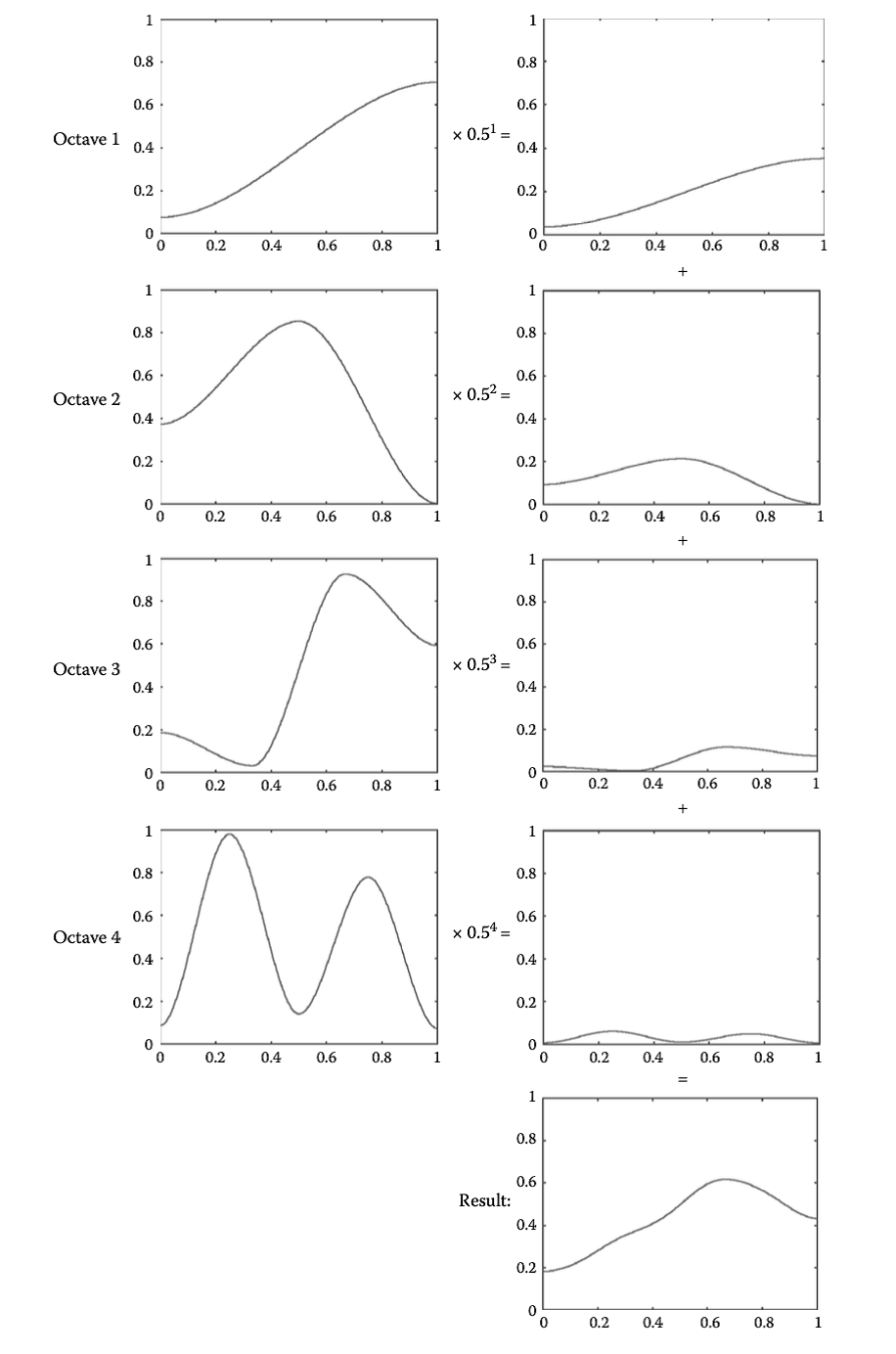
Figure 3. Process of the production of octave signals [2]

Apart from Octaves, the values of Lacunarity and Persistence are usually required in the generation of a Perlin noise map. In order to control the ratio at which each octave is increasing its size, two terms are defined: Lacunarity and Persistence. To make it simple, lacunarity controls the increasing rate of frequency of each octave, and persistence controls the decreasing rate of amplitude. An extra seed value would also be added to generate the pseudo-random numbers so that by entering the same seed value, the same noise map could be obtained.

Unity also has the function to calculate 2D Perlin noise. It yields the Perlin noise value within the range of 0.0 and 1.0. Despite the two-dimensional nature of the noise plane, we can disregard one coordinate and extract the noise by solely considering a single dimension.

e.g., movement direction (using Perlin noise):

4. General Principles in Randomized Algorithms

Although there are many types of algorithms that could be applied to games, randomized algorithms stand out among them. What are the reasons behind it? This section analyzes and summarizes the common principles of randomized algorithms and its general properties.

4.1. Foiling an Adversary

A randomized algorithm could be regarded as the probability distribution on a large set of deterministic algorithms. In classical analysis of a deterministic algorithm, there is usually an imaginary ‘adversary’ who can always design a suitable input to foil the whole algorithm and slow down the running speed. This input would keep changing in order to adapt different deterministic algorithms. However, for a randomized algorithm, it is unlikely for the adversary to make a single input that could foil the whole algorithm. In other words, it means that using a randomized algorithm could prevent strange inputs that increase the processing difficulties and decrease the overall performance of an algorithm [17].

For example, when there is a tree with n leaves, with each leave containing different Boolean values. Solving such a problem could be challenging for deterministic algorithms since they may be forced to read all the values in order to get the exact number of leaves n. A simple and easy way to do this would be using a randomized algorithm, as it could generate a general formula for any input given (e.g. n = n*3+1) [17].

4.2. Random Sampling and Reordering

This principle would be useful when analyzing a relatively large data set, such as the total population of a certain country. It is almost impossible to extract all the data and observe them one by one. Therefore, through the randomized algorithm, we could randomly select a certain number of samples for reference, and by rearranging them into a correct order based on their weights, we could speculate on the general trend [17].

Another use of reordering data is to evaluate the algorithm more precisely. For example, for an algorithm called X, may perform well in general, but there is a probability for it to run badly on certain input values or even have some system bugs. By reordering the data, we could check the real performance of certain algorithms or programs [17].

4.3. Abundance of Witnesses

This principle could help people check if an input has the specific property they are looking for. The most efficient way to verify a hypothesis is to find a witness. For example, in order to show a number is not a prime number, we only need to find one of its non-trivial factors and that is enough to prove its identity. If the scale is quite large, then a randomized algorithm could be the key to solving such a problem. By repeating generating an output, the probability of finding one of the witnesses could be increased again and again. Eventually, the probability would infinitely approach or equal to 100% [17].

4.4. Fingerprinting

A fingerprint is defined as a shorter message that could represent an object with a larger size, which has many useful properties. It could be a list of numbers, a line of code, or even simply a special character. Using random mappings, fingerprints could be easily gotten and matched to the correct objects. This could be very useful during programming parts. For example, by comparing the footprints, whether two strings are identical to each other could be easily figured out [17].

4.5. Load Balancing

Load balancing refers to evenly distributing limited resources to different needs. For example, when our computer consumes a lot of energy, through randomization, it can easily distribute the energy evenly to the components, such as the arithmetic logic unit (ALU) or Control Unit (CU) with greater demand, so as to prevent the system or a certain program from suddenly not responding and terminating [17].

5. Feature-Analysis of Common Randomized Algorithms

As several randomized algorithms are described, the strategies they use to generate randomness are obviously different in some cases. Since the inspirations of them are various, some of them have some principles, but some of them are definitely different at all. Considering this, in this section, the advantages and disadvantages, or just the features of the randomized algorithms, which are mentioned above, will be analyzed in a particular way according to the performance in video games.

5.1. Gaussian randomness

This type of randomness is not only prevalent in statistics but also in the natural world, encompassing the velocity of runners or vehicles, the stature of humans, trees, and other beings, as well as various other physical or mental attributes. The central limit theorem (CLT) elucidates the rationale behind the substantial presence of the normal distribution in our lives, as opposed to the uniform distribution. In numerous instances, when dealing with identically distributed and independent random variables, the sampling distribution of the standardized sample mean converges towards the standard normal distribution, even when the original variables themselves are not normally distributed. Since almost everything in the whole world has multiple contributing factors, each of the contributing factors has random aspects, the performance of random aspects leads to a Gaussian distribution. Accordingly, in the realm of video games, Gaussian randomness may evoke a greater sense of naturalness amongst players, as opposed to the type of randomness generated solely through the utilization of the rand() function.

In a video game, Gaussian randomness can be used to create a bullet or projectile spread. Both enemy NPCs and player characters may require their bullets or projectiles to have a smoothly randomized spread. Traditional randomization functions distribute the spread equally in a narrow target position and the slightly wider surrounding area. However, through the utilization of Gaussian randomness, the dispersion can be dispersed in a manner that optimizes projectiles striking the desired location while minimizing those striking the encompassing vicinity. Furthermore, the bullet dispersion can be influenced by additional. Implementing Gaussian randomness in character stats allows for small variations in speed, acceleration, size, health points, damage, critical hit chance, and more. Including these variations enhances gameplay by creating natural and balanced outcomes.

It’s true that Gaussian distribution exists in numerous parts of the natural world due to the probability that most natural things are influenced by multiple factors, but in a video game, there are still abundant of elements that could be simply determined by a single factor. In many cases, if the rate of the importance of each of the element of a randomized choice is directly the same for the player, Gaussian randomness might lose its superiority [2,3]

5.2. Filtered Randomness

As the purpose of the creation of Filtered randomness, Filtered randomness can avoid the problem of “too random” and benefit players according to players’ aspirations in the short term. Compared to Gaussian randomness, which still has a high-fixed randomized consequence just like the curve shows, the consequences of Filtered randomness are much more custom. Game designers define the rules of the replacement due to their needs. Generally, perfect enough rules give Filtered randomness a huge possibility.

Nonetheless, the rules of the replacements must be considered seriously since the actual implementation of this method is subjective. It is crucial to consider that incorporating excessive regulations or establishing overly stringent guidelines would diminish the level of unpredictability, which could have an adverse impact on the game or even create the perception that the element of randomness is non-existent, a circumstance this approach endeavors to circumvent [2,3]

5.3. Random Walk

One of the most important features of random walk is that the implementation is a continuous path and each element has a certain relationship to others. As a result, it usually be used in PCG, or just the generation of the dungeons of Roguelike games.

However, this advantage also affects a video game in a negative way sometimes, or the just called limitation. When we are using a Random walk, especially out of the map generation, the continuity of this algorithm might do harm to video games. For example, in the context of simulating a game world or generating commodity prices in a procedurally generated universe, we often use a random walk as a simple and efficient method. To generate this random walk, we start with an initial value, x0, and at each step, we add a sample from a normal distribution. This process allows x to fluctuate randomly around the starting point. However, what if we need to determine the value of x in the future, such as two days from now? Alternatively, if the player observed x having a specific value two days ago, what should its current value be? This scenario presents the challenge of extrapolating a random walk.

One approach to resolve the extrapolation predicament is to expeditiously simulate the absent portion of the stochastic trajectory. Nonetheless, this could potentially be computationally unfeasible or undesirable, particularly when we are simultaneously modeling a substantial number of stochastic trajectories, as may be the circumstance if they epitomize prices in a virtual economy. Fortunately, we can employ statistical methodologies to precisely determine the distribution of the stochastic trajectory two days subsequent to its most recent observation, solely relying on the aforementioned last observed value in accordance with the central limit theorem.

Also, the game cannot simply regenerate the elements each time, as it would lead to an excessive waste of time. At the core of a computer-generated random walk lies a random number generator, which can be manipulated to generate and replicate a particular sequence of numbers by utilizing a seed. By documenting the seed values employed in constructing different segments of a random walk, those segments can be precisely reconstructed if and when necessary [12].

5.4. Perlin Noise

Perlin noise could generate random points that are related to each other, which is quite similar to a random walk. The main advantage of Perlin noise over other fractal methods, such as the mid-point displacement method, comes from the hierarchical structure of Perlin noise. The hierarchical structure allows for a very wide range of spatial patterns.

A possible disadvantage of Perlin noise is that, like all procedural generation methods, specifying the appropriate set of parameters can be bewildering, especially when the parameters can interact in non-intuitive ways so that successful application of procedural generation methods such as Perlin noise can require a lot of experimentation. Perlin, the developer, did not apply for any patents on the algorithm, but in 2001, he was granted a patent for the use of 3D+ implementations of complex noise for texture synthesis. Simplex noise has the same purpose but uses a simpler space-filling grid. Simplex noise alleviates some of the problems with Perlin’s “classic noise”, among them computational complexity and visually-significant directional artifacts. Simplex noise improves on some of the shortcomings of Perlin noise, notably its inefficiency in higher dimensions and directional artifacts [18].

Due to the features above, here are some possible applications of Perlin noise for game AI [2]:

•Movement (direction, speed, acceleration);

•Layered onto animation (adding noise to facial movement or gaze);

•Attention (guard alertness, response time);

•Play style (defensive, offensive);

•Mood (calm, angry, happy, sad, depressed, manic, bored, engaged);

6. Relevant Applications in Specific Video Games

As game replayability is explored by game designers more deeply, the randomized algorithm has been applied to a wide range of computer games. Although the algorithm itself is relatively easy to understand, how to implement the rules into the game itself is difficult. This section discusses applications of randomized algorithms in several common game categories and the mechanisms behind them.

6.1. Rogue-like Games

Rogue was the originator of rogue-like games and also one of the earliest dungeon-crawling games built on the UNIX system [19]. It took the definition of randomness in games further by relying heavily on the use of procedural generation. A good example would be the randomization of items. A tin wand in one level could be totally different from a tin wand from another level, with distinct functions and appearance [20].

According to “Decoded: Rogue” [21], whenever generating a new level with PCG, rogue follows a set of rules that will be executed in order:

1)Remove last-level data (layout, rooms, monsters, items, etc.)

2)Create up to 9 rooms of sizes from 4x4 to 25x7, including border wall

3)Add possible gold and monsters to each room during creation

4)Connect rooms with passages

5)Add items to random rooms (and Amulet of Yendor if level 26)

6)Place the level exit stairs

7)Place traps with increasing probability based on level number

8)Add the hero to a random room at a random position

The source code perfectly follows the rules listed above. It is worth mentioning that, in addition to the generation of each level, the generation of specific rooms, specific items, and random monsters also has a set of independent generation rules [16].

After Rogue, many dungeon-crawling games gradually began to imitate their operation mode and creative concept, and people called them ‘roguelikes’ or rogue-like games. Some famous examples include Hack, NetHack, Moria, Ancient Domains of Mystery, and the recent critically acclaimed The Binding of Isaac and FTL: Faster than Light [19,20].

As mentioned in the background section, rogue-like game generation looks more like a simple form of Random Generation rather than the Procedural Content Generation (PCG) that the public refers to now, as it is partially based on pre-written codes and not fully deterministic by computer. This statement may sound weird since lots of academic papers refer to Rogue or several rogue-like games to standard examples of PCG. A reasonable explanation is that in the past when PCG was not deeply studied by programmers or game developers, rogue-like games could indeed be included in this big group. But with the development of the game factory, more and more video games using more advanced PCG technologies have been made. For example, No Man’s Sky created a deterministic universe completely set up by computers themselves, using procedural generation, including over 18 quintillion random planets [22]. By comparison, the randomness of rogue-like games is only in the order in which different rooms and different items are generated and appear, not the entire content of the game. For example, in The Binding of Isaac, each level is generated simply by stitching predefined hard-coded rooms together to form a new arrangement. Therefore, it is not considered to be precise to say rogue-like games are 100% generated by PCG [5]. There is still no doubt that Rogue and several other rogue-like games have created a milestone in the history of PCG, although they now seem a bit different from how people define it.

6.2. Sandbox Games

Sandbox games are games that give players the greatest degree of freedom and creativity. Usually, in a sandbox game, players do not have a clear goal set in advance, and they could spend most of their time building, constructing and modifying interesting elements inside the game.

Sandbox games are composed of rich randomized algorithms starting from the map generation. Take one of the most classical Sandbox games, Minecraft, as an example. The most attractive part of Minecraft would probably be its huge infinite map. Every time the player comes to the border of the available loaded map, the game will automatically generate and load a new ‘chunk’, allowing the player to continue exploring far away. In fact, Minecraft is only virtually infinite, and the real size of the word depends on your device’s hardware and computer system. For instance, a 32-bit system computer generates a different number of blocks from the spawn point compared to a 64-bit system. And even if a computer could generate much more blocks than average, the area that the player could reach is still limited to the size of 60,000,000 x 60,000,00, set by Minecraft itself (Fig.4). Although this number is quite small relative to infinity, the interesting fact is that it is almost seven times larger than the surface area of the Earth [23].

Figure 4. Minecraft World Size [23]

Minecraft has used various noise maps (especially Perlin noise) to construct its structure. In the early versions, the game developers used three basic noise maps to classify biomes, which are the terrain height, the temperature, and the rainfall, respectively, as shown in Fig.5. For example, if a place consists of noise maps of high temperature and low humidity, then it would be the desert biome. However, as the game develops, the use of noise maps to control randomness in Minecraft is also changed. The following sub-sections will discuss the map generation of Minecraft in a more specific and up-to-date way [23].

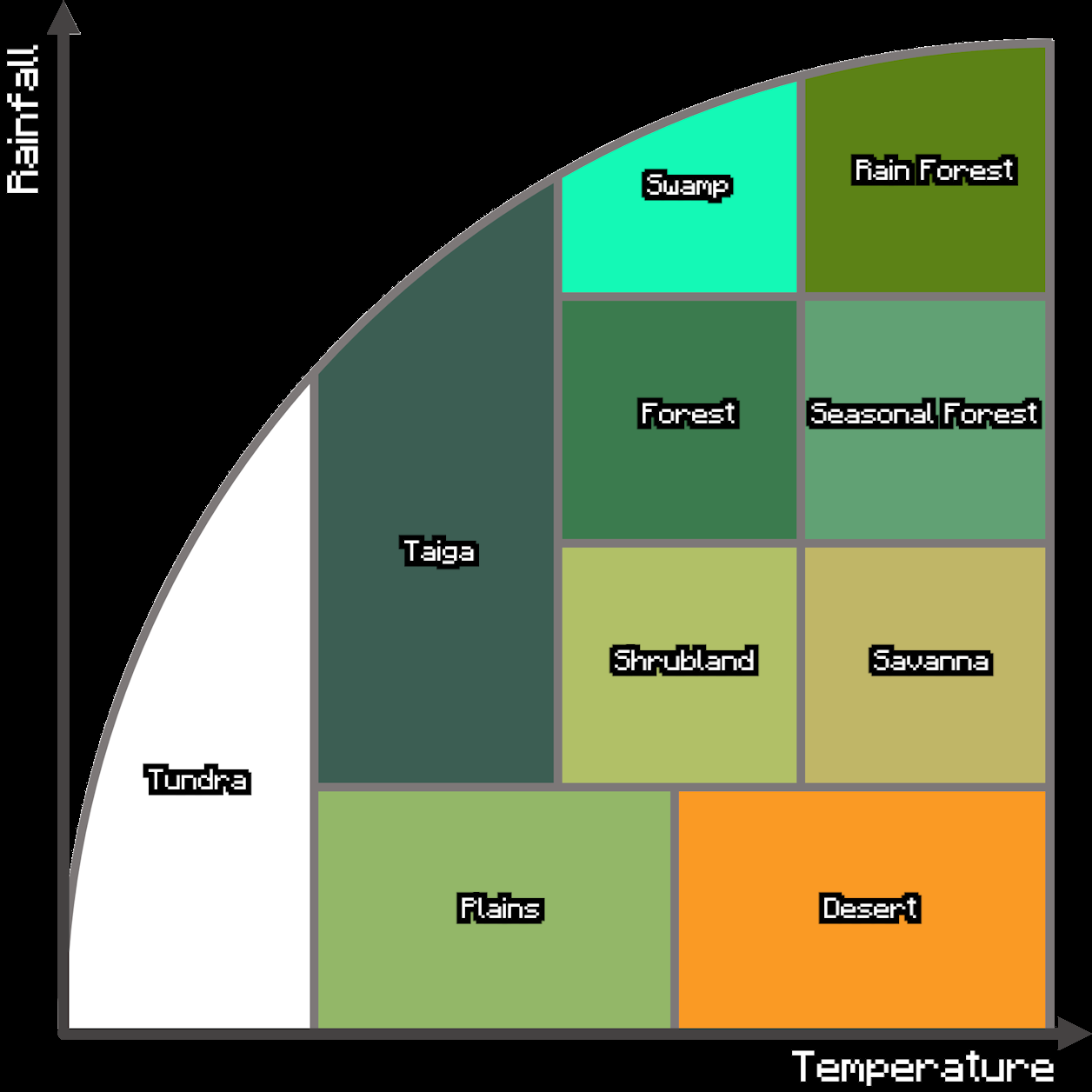
Figure 5. Early Construction of Minecraft Maps [23]

1) Biome Map: The biome map in Minecraft is often composed of four layers, with one stacking on another. One layer contains codes for land formation, two layers for ocean formation, and an additional layer for extra details to be added, such as hill variants of different biomes [23].

A noise map of two colors representing land and ocean would start being generated at the same time. The ratio of land to ocean is 1:10, so any number rolled other than 1 could only generate water. Each pixel on this noise map represents 4096 blocks in the game [23].

Apart from that, Minecraft is also using ‘zoom’ techniques to increase the randomness of the biome map. For example, after adding a zoom on the original noise map, one pixel now represents 2048 in-game blocks, which is half of the previous size. By adding multiple zooms to the noise map, the sense of boundaries between different biomes could become blurred and mixed together since now one pixel of the noise map could stand for even fewer blocks. This increases the chance of land expanding into the adjacent river, which also increases the variety of the land’s appearance [23].

2) Temperature (Climate): Temperature is also an important element in Minecraft because each biome will randomly generate different weather every day in the game to increase the variation of the biome [23].

Minecraft uses a big list of climate layers to define the temperature in each different region. There are basically four temperatures: Warm, Temperate, Cold or Freezing. The possibility of being assigned to any of the temperatures is 1:4, which is settled. And then, as mentioned above, Minecraft would figure out the biome that this region would belong to, according to the temperature assigned. For example, Warm regions have a 50% chance of turning into a Desert, 33% into a Savanna, and the remaining 17% into Plains [23].

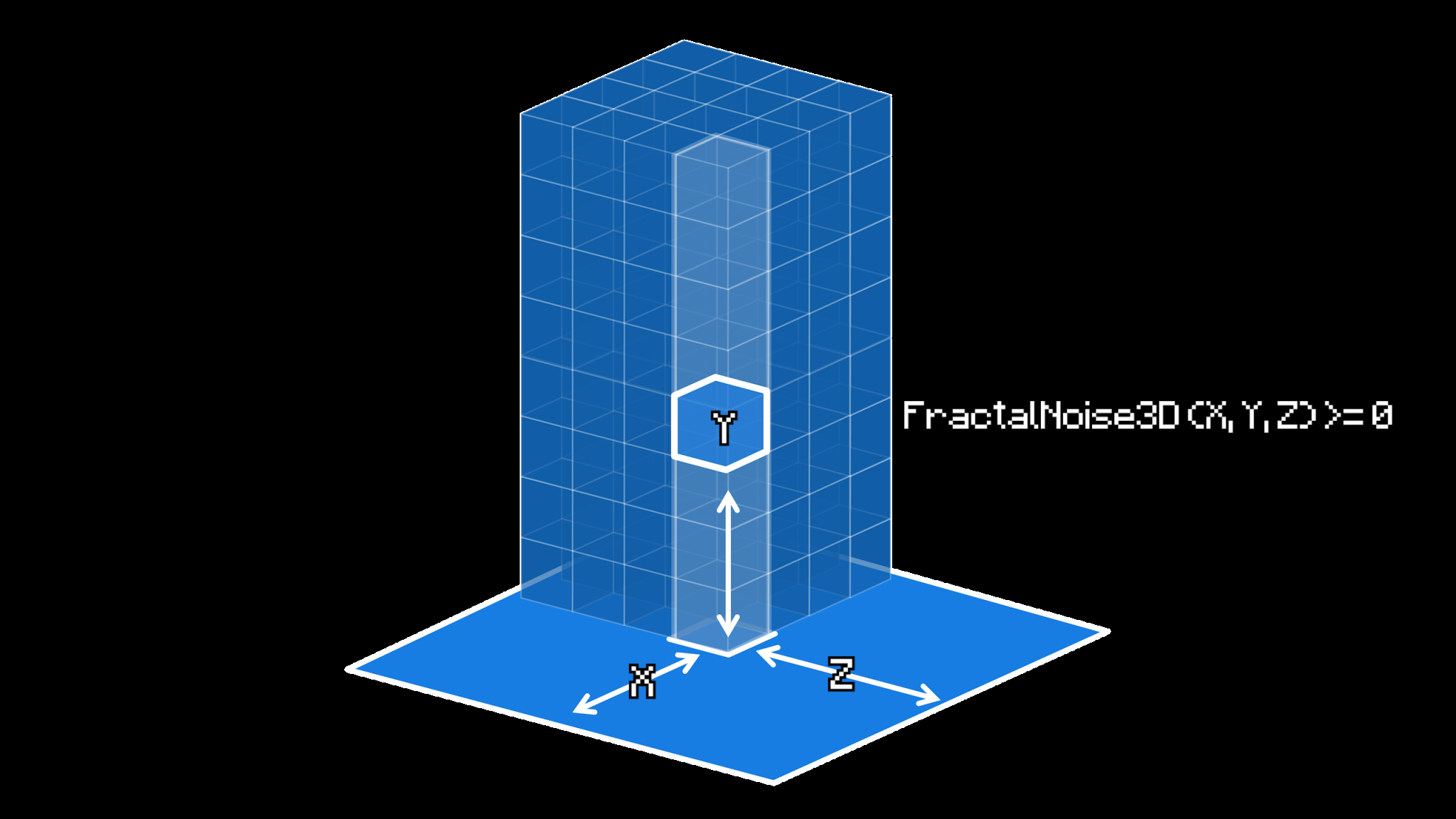
Figure 6. Terrain Height Generation by Fractal Noise [23]

However, there is a huge problem. For instance, it is possible for a desert biome to be next to a glacier biome, which goes against the common sense of nature. To avoid this and increase the smoothness of the game, Minecraft adds a few more layers of data as details. Finally, any warm land adjacent to a cool or freezing region would turn temperate, and any freezing land adjacent to a warm or temperate region would turn cold, which also increases the overall randomness of each biome generated [23].

3) Terrain Height: How to manage different terrain heights could be one of the most challenging parts when designing Minecraft since this is a 3-dimensional problem, and noise maps, including the famous Perlin noise, are mostly used to solve 2-dimensional generation. As a result, a technique called “fractal Brownian motion noise”, or fractal noise, is used (shown in Fig.6) [23].

The fractal noise is made up of multiple Perlin noise maps stacked together, each of which has different components and levels of detail. This property makes the terrains generated from fractal noise look more natural and real [23].

Starting from the top border of the whole world ( y = 255), a calculator would continue moving downwards until it reaches the bottom border to calculate the fractal noise value at each specific (x,y,z) location along that vertical column. Then, the first y-coordinate for which the fractal noise is equal to zero would become the final height of the terrain at that (x, z) coordinate, and the calculator would stop moving and calculating [23].

This is basically how different noise maps are used in Minecraft or Sandbox games to generate the game maps randomly while maintaining their smoothness.

6.3. Multiplayer Online Battle Arena (MOBA) Games

Multiplayer Online Battle Arena (MOBA) games are derived from a branch of the Real-Time Strategy (RTS) games. In this game, players control and play characters with different abilities or attributes. Eventually, when the player or player’s team invades and destroys the enemy’s base, the game ends. During this process, computer-controlled units would be spawned automatically to help the player attack the enemy team, with a fixed path. However, different from typical RTS games, players in MOBA games usually are not given the power to construct or repair their buildings. All they can do is simply destroy the buildings that the system has created before the game starts [24].

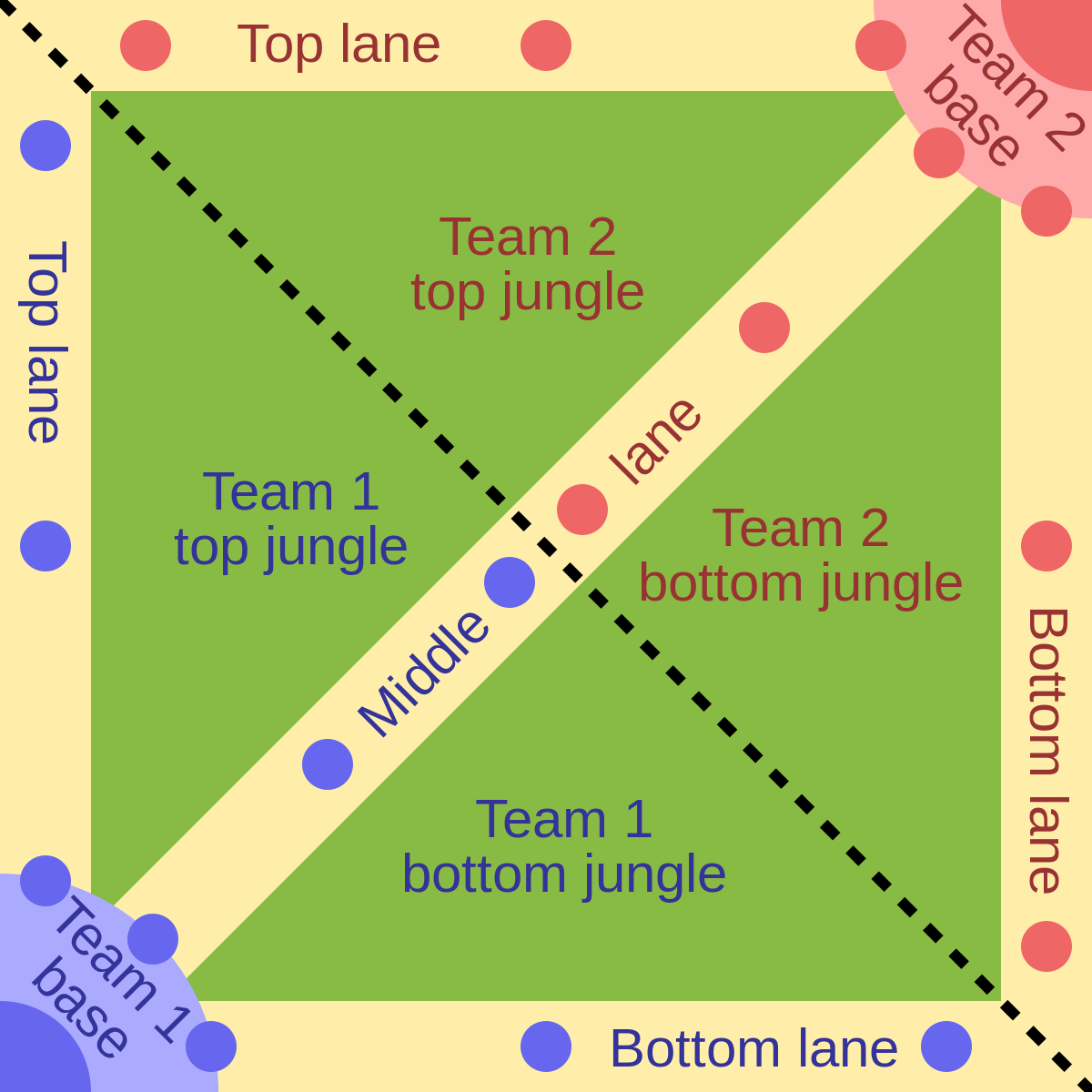
Figure 7. A Standard Map Structure of MOBA Games [24]

As shown in Fig. 7, MOBA games usually have settled maps and limited winning strategies. It is hard to associate them with the word “randomness”. But one interesting fact is that, except for the map, in many MOBA games, there are randomly spawned wild monsters. Players can gain a strengthening effect by killing them, which can not help but speed up the game and greatly increase a team’s possibility to win. For instance, in League Of Legends (LOL), the system randomly generates one out of six dragons at a specific time point as an epic monster in a dragon pit as its spawn point. This type of monster is called the “Drake” in the game. When a team kills this dragon, they could get corresponding extra abilities according to the predefined attributes of that randomly generated dragon [25].

Even though LOL official (Riot) rarely shares their source codes with the players, this level of randomness is fundamental and can be understood easily. The programmer only needs to assign different dragons a different number, and by comparing the randomly generated number from the PRNG, the system would evoke related functions or commands to set a spawn for a corresponding dragon. Fig. 8 shows different dragons generated randomly.

Figure 8. Different randomly generated dragons in League Of Legends [26]

Another element in MOBA games that uses randomized algorithms is the occasional critical hit, also known as the “crit”. It could usually be frustrating since a well-played player may lose the game because of a random lucky critical strike from a less-skilled player. Hence, game developers are always trying to find the best way to reduce the harmful effects of randomness and control its degree in an acceptable range [27]. Figure 9 shows the observed results of critical strike rates in League of Legends

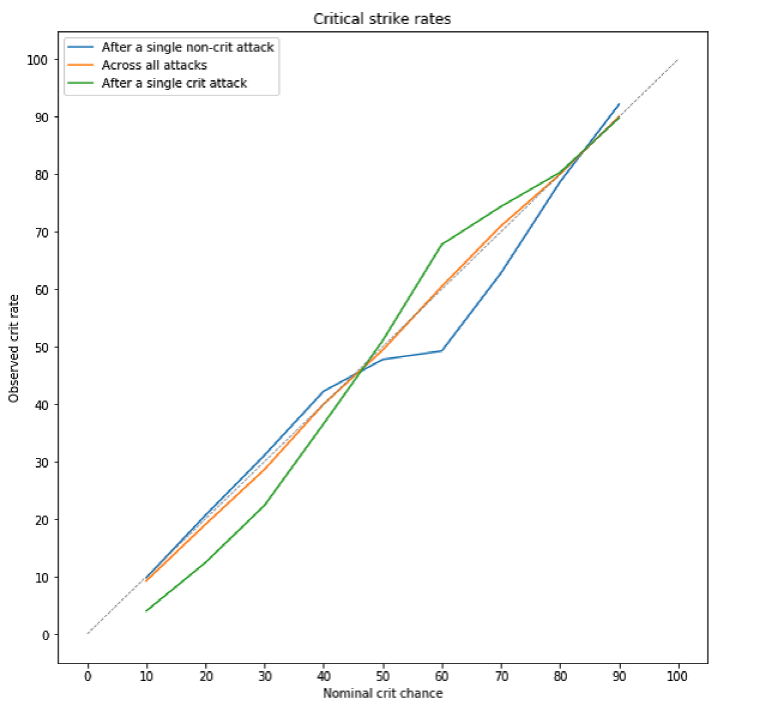
Figure 9. Observed Results of Critical Strike Rates in League Of Legends [27]

In the update of Riot’s patch v1.0.0.109, Riot implemented a new algorithm called ‘crit smoothing’. Prior to this, players assumed that if they bought a piece of equipment with a 60% crit chance, each of their attacks would have a 6 out of 10 chance of crit somewhere. However, according to Fig.6 measured by Nathan L., he found that the independence of each attack was no longer the truth [27].

It indicates that the lower the nominal crit rate, the less likely to crit again after the first crit. While for players with high nominal crit chance due to their equipment are more likely to crit again. At the same time, as shown in the figure, no matter what your nominal crit rate is, the real crit value will eventually return to a normal and stable value after two to three crits, which is shown by the orange line [27].

This example shows the importance of controlling randomness in video games, which can not only reduce the uncertain factors of the game but also increase the player’s game experience and the fairness of electronic competition.

7. Conclusion

In this literature review paper, we discuss the definition of Pseudo-random Number generator (PRNG) and Procedural Content Generation (PCG) in the background section. In the next section, the concept of a randomized algorithm, including its different branches, is further introduced. Then in the third and forth parts, we explore the reasons for programmers and game developers to use randomized algorithms, together with its benefits and weaknesses under different situations. In the final section, several classical examples of applications of randomized algorithms are listed with the principles and source codes.

Acknowledgement

Junqi Zhao and Peiyuan Li contributed equally to this work and should be considered co-first authors.