1. Introduction

1.1. Gauge theory

Mass is a quantity in physics that is hard to explain. Why do objects, or more specifically, particles, possess mass? We use photons to determine why some particles have mass and others do not. The first thing that needs to be mentioned is gauge theory. This is a type of field theory in which the fundamental laws and equations of motion are invariant under certain transformations, known as gauge transformations or local transformations. These transformations are local, meaning they can vary in spacetime [1-3].

Photons which we now know to be massless. Scientists first apply the Higgs mechanism to the Abelian \( U(1) \) gauge theory to show how the mass of the corresponding gauge boson (photon) is produced. Then, the example of the Abelian theory is extended directly to the non-Abelian Glashow-Weinberg-Salam theory, also known as the electroweak standard model. This theory can be described as a gauge theory with the symmetry groups \( SU(2) × U(1) \) .

Explaining the weak interaction involving the exchange of spin-1 gauge fields and the electromagnetic interaction. The weak interaction involves three heavy bosons, \( W± \) and \( Z \) .

\( L=-\frac{1}{4}{F_{μv}}{F^{μv}} \) (1)

where

\( {F_{μv}}={∂_{μ}}{A_{v}}-{∂_{v}}{A_{μ}} \) (2)

\( {A_{μ}}(x)→{A_{μ}}(x)-{∂_{μ}}η(x) \) (3)

(1) is the Lagrangian gauge invariant dynamical term. \( L \) is invariant under the local gauge transformation (3), for any \( η \) and \( x \) .

Let’s add a mass term to the Lagrangian of the photon, which the equation looks like this:

\( L=-\frac{1}{4}{F_{€v}}{F^{€v}}+\frac{1}{2}{m^{2}}{A_{€}}{A^{€}} \)

If we substitute the local transformation here into the equation which is \( {A_{μ}}(x)→{A_{μ}}(x)-{∂_{μ}}η(x) \) , and we expand the bracket. We quickly realize that the mass term violates local gauge symmetry. Therefore, \( U(1) \) gauge symmetry i the photon must be massless.

If we introduce a more complex scalar field with charge \( (-e) \) and link them back io we will still observe they are invariant.

The photon is a gauge boson, and by applying the process described to all bosons and other fundamental particles, we arrive at an equivalent conclusion: to maintain the gauge theories, the intrinsic properties of all fundamental particles inherently lack the term associated with mass.

Following the discovery of the Higgs field, there occurred a significant transformation in the Lagrangian of particle mass terms. The Higgs field is associated with spontaneous symmetry breaking and imparts mass to particles. Through the Higgs mechanism, fundamental particles interact with the Higgs field, acquiring mass as a result. This interaction leads to a non-zero vacuum expectation value for the Higgs field, breaking gauge symmetry, thereby conferring mass upon certain gauge bosons and endowing fermions such as quarks and leptons with mass. Consequently, the discovery of the Higgs field elucidates the origin of particle mass, laying a foundational basis for the masses of particles within the framework of the standard model.

1.2. Spontaneous symmetry breaking

In particle physics, spontaneous symmetry breaking is crucial in understanding the origin of mass and the behavior of elementary particles. In the standard model of particle physics, spontaneous symmetry breaking is exemplified by the Higgs mechanism.

The Higgs field is a scalar field that permeates all of space and plays a key role in giving mass to certain particles. The universe is composed of fields. However, most of these fields are in a closed state, meaning they have a value of zero in space. Particles are small oscillations in these fields, and when a field deviates from its natural value, a small amount of energy is produced. The Higgs field is an exception, as it doesn’t have a zero value, even in space. Fields have specific values everywhere, and the Higgs boson oscillates around this value rather than around zero. All of this is related to energy. Placing a ball on top of a hill, physicists refer to as having potential energy; it doesn’t do any work and remains calmly there, yet it can release energy if allowed to roll down the hill. When this occurs, it gradually converts potential energy into kinetic energy by increasing speed. However, it also encounters other stones, experiences air resistance, and emits noise during its motion – all of which expend energy. As a result, by the time it reaches the foot of the hill, its original energy has transformed into sound energy and thermal energy, and the ball comes to a complete stop.

Fields behave similarly as well. If we excite them from their preferred state of equilibrium, we bestow upon them potential energy. The field starts oscillating and depletes this potential energy by transferring energy to other fields, ultimately calming down. The exceptional aspect of the Higgs field lies in its energy at rest, not being zero; its minimum energy corresponds to a field with 246 GeV. This value is established through experimentation, determining the energy associated with coupling the W and Z bosons to other particles.

The number 246 GeV is not the mass of the Higgs boson; it’s the field value in space. The mass of the Higgs boson informs us about the force required to set it in motion. Put differently, it tells us how much energy we need to input into the oscillation of the field for the Higgs boson to manifest as an independent particle. On the other hand, the field value is an entirely different aspect, describing what the field is doing when it’s in a completely stationary state. To clarify why the field value of the Higgs field is 246 GeV and not 0, let’s consider an analogy with a pendulum hanging from the ceiling. The behavior of this pendulum is akin to that of a regular field, with its lowest energy state being when the pendulum is vertically suspended at the top of its arc. We can provide energy to it by pushing it away from that position. If we let go after pushing, it will start swinging back and forth, eventually losing energy due to air resistance and friction, coming to a stop.

Now, let’s imagine an inverted pendulum with its pivot point fixed on the floor instead of the ceiling. The mechanics of the pendulum’s motion remain mostly the same, but its behavior is entirely different. The inverted pendulum has energy when it’s in the vertical position; before that, it’s in its lowest energy state. However, now there are two possible orientations for this lowest-energy state: one on the left side of the floor and the other on the right. But regardless of which side, the pendulum is lying on the floor, pointing either left or right. The Higgs field is analogous to this inverted pendulum. Attaining a state of zero energy requires expending energy. Its lowest energy state is when the field holds a fixed value everywhere, much like a pendulum’s bob rests on either the left or right side of its pivot. This is why the vacuum is filled with the Higgs field, allowing other particles to interact within it; it represents the lowest energy configuration. The field value is akin to a deviation from the vertical position—regular fields seek to be at 0 value. In contrast, the Higgs field desires to deviate from zero, much like the inverted pendulum prefers to lie on either the left or the right side. Imagine an electrically charged particle interacting with a nonzero electric field. Because the point field value is not zero, the charged particle can acquire energy within that electric field. A similar scenario applies to the Higgs field. The rule is simple: if a particle doesn’t directly interact with the Higgs field, it possesses zero mass. If a particle interacts directly with the Higgs field, it has nonzero mass. The magnitude of the mass is directly proportional to the strength of the interaction between the particle and the Higgs field. For instance, particles like electrons and up quarks, down quarks, which interact with the Higgs field weakly, have smaller masses. On the other hand, particles like top quarks, which interact more strongly with the Higgs field, have larger masses.

The universe was once very dense, with much more energy packed into a much smaller volume than now, so the temperature was extremely high. Using the analogy of a pendulum mentioned earlier, high temperature means more intense molecular motion, causing the pendulum to constantly swing. In this scenario, the motion of the pendulum becomes symmetric. The same thing also happens in the Higgs field. In the very early universe, the temperature was extremely high, and the Higgs field was continuously pushed and prodded. As a result, its value at any point in space oscillated around zero. So, in the early universe, symmetry was restored. This period is roughly one-trillionth of a second after the Big Bang. During this moment, the Higgs boson would evolve from a zero value to a non-zero value.

In essence, the presence of the Higgs field leads to the spontaneous breaking of symmetry for fundamental particles, granting mass to certain particles and revealing that particles like photons remain massless because they don’t directly interact with the Higgs field. The Higgs mechanism holds crucial significance within the framework of the Standard Model.

2. Nambu-Goldstone Theorem

When a spontaneous symmetrical system breaks, Goldstone bosons are always gained, and this is also a feature of spontaneous symmetry breaking.

Let’s have a brief review here using a little m. Consider a non-linear Nambu-Goldstone field with a simple model \( U(1)→{z_{2}} \) at the energy scale f as a minimal case:

\( U={e^{iϕ/f}} \)

With a transformation \( ϕ⟶ϕ+ϕf \) , where \( 0 \lt θ≤2π \) , the low energy effect theory is invariant under transformation \( U⟶-U \) , corresponding to \( θ=π \) , then the lower-energy \( e \) Lagrangian of the field as below:

\( {L_{eff}}=\frac{1}{2}{f^{2}}{∂_{μ}}{U^{†}}{∂^{μ}}U+O({∂^{4}}) \)

The first term here only gives a kinetic term, and the interaction with derivative couplings is included in higher orders.

3. Higgs Field Mechanism

Before the Higgs Field, consider the gravitational field and the electromagnetic field. Consider only potential energy in the gravitational field,

\( U=-\int _{{h_{1}}}^{{h_{2}}}mg(h)dh \)

Similarly, we could obtain a function of energy for a particle in an electromagnetic field:

\( {U_{a}}=V(\frac{1}{2}{ε_{0}}{E^{2}}+\frac{1}{2{μ_{0}}}{B^{2}}) \)

and we could also use Lagrangian to describe the energy in the electromagnetic field,

\( L=\frac{1}{2}m\dot{{\vec{r}^{2}}-q\dot{\vec{r}}}∙\vec{A}-qϕ \)

Although we could not obtain a similar term for the gravitational field, we still know they have the same fundamental mechanism.

Consider special relativity with a rest particle of mass m and charge \( q \) in an electrostatic field, we then get another form for energy:

\( U=qE+\frac{1}{2}{ε_{0}}{E^{2}}+m{c^{2}} \)

So here, we could assume a similar form of energy for the Higgs field. But we need to solve another important thing: we do not know if the Higgs field is a vector field or not. Before that, we already knew that the Higgs bosons are of spin 0, so to fit the Higgs bosons, the Higgs field should also be of spin 0, which is a scalar field. Due to the assumption above and also classical quantum field theory, we obtain:

\( V(ψ)={M^{4}}(1-2\frac{{ψ^{2}}}{{v^{2}}}+\frac{{ψ^{4}}}{{v^{4}}}) \)

where \( M \) and \( v \) are coupling constants. From the standard model, we know that particles gain masses through interacting with the Higgs field. First, let’s go back to the general Lagrangian. In general, there are three parts in Lagrangian: the GaugeGauge field, Fermions, and the Higgs field:

\( L=\frac{1}{2}{∂_{μ}}ϕ{∂^{μ}}ϕ-\frac{1}{2}{m^{2}}{|ϕ|^{2}}-V(ϕ) \)

The last term here is the potential term for Higgs field. From the Higgs mechanism, when the Higgs field is excited, Higgs bosons will be produced and other particles are caused to interact with Higgs field at the same time.

We obtain the function of potential of the Higgs field after some complex derivation:

\( V(ϕ)={μ^{2}}{|ϕ|^{2}}-λ{|ϕ|^{4}} \)

4. The process to prove the existence of Higgs boson

How to find the Higgs boson? Researchers used to predict the substance after the Higgs particle decay. The Higgs boson has a very short lifetime, so it easily decays into other particles once it is produced. Researchers list several possible dacy formulas to predict the substances after the Higgs particle decay by conservation laws such as conservation of charge, and conservation of lepton. Researchers speculated and confirmed through experimental data that particles generated after the decay of the Higgs boson were possible. In 2012, they chose to detect pairs of photons to demonstrate the possibility of the existence of the Higgs boson because photons are very stable and do not decay, resulting in a long lifetime.

This is the formula of decay of Higgs boson:

\( H⟶γγ \)

\( H:Higgs boson \)

\( γγ:photon pairs \)

In 2012, CERN discovered evidence of the decay of the Higgs boson. CERN used high-energy proton beams to collide with each other in accelerators to generate Higgs bosons.

This is the Animation of the reconstructed mass from Higgs candidate events in two-photon decays:

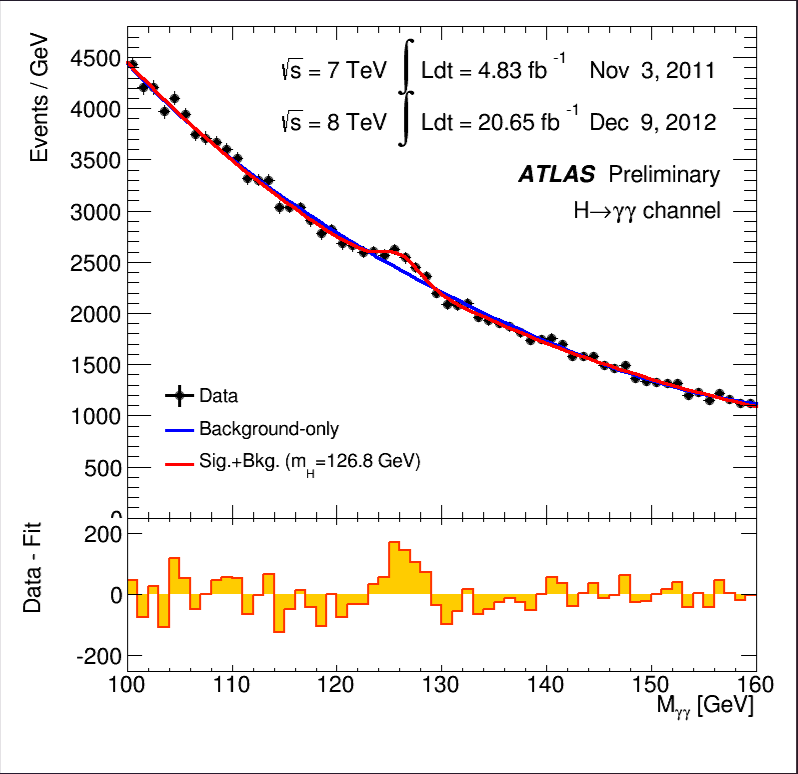
Figure 1. ATLAS Experiment, CERN [4]

Through the use of charts (figure 1), an interesting phenomenon can be observed: generally, the higher the energy of photon pairs, the fewer the number of photon pairs. However, in an experiment conducted in 2014, a small peak was discovered at 125 GeV. Further research indicated that this peak was caused by the decay of the Higgs boson, resulting in the production of approximately 500 photon pairs.

To determine the mass of the Higgs boson, we can apply Einstein’s mass-energy equation, \( E=mc² \) . Since photons have zero mass, the mass of the Higgs boson is entirely converted into the energy of the photon pairs. Therefore, we can conclude that the mass of the Higgs boson is approximately 125 GeV. It is important to note that this is an approximate value [5, 6].

5. Conclusion

The discovery of the Higgs boson in 2012 was an epoch-making event in particle physics research. It plays a crucial role in the “standard model” of particle physics, bringing mass to fundamental particles through the mysterious symmetry breaking mechanism, and is associated with the unpredictable quantum vacuum information. It is also believed to play an important role in the very early stages of cosmic evolution. This article describes the theoretical background and particle characteristics of the Higgs boson, Experimental exploration, research status and prospects from a popular science perspective, unveils the mysterious veil of the Higgs boson, and briefly tell its past, present, and future

Acknowledgement

Yutong Bai, Yufan Liu, Yonghang Gao, and Junwei Chen contributed equally to this work and should be considered co-first authors.