1. Introduction

China’s economic growth has increased energy demand, leading to environmental challenges that conflict with the goals of ‘Carbon Peak, Carbon Neutral’ [1-3]. The pursuit of renewable energy, especially solar energy, is key to achieving sustainable development. Solar thermal power plants utilize strategically positioned heliostats to convert solar radiation into electricity, and their design is crucial for efficiency and cost-effectiveness. Current research on mirror field optimization is limited by a lack of the detailed mathematical models and the performance evaluation methods, so further research is needed to refine layouts and enhance the energy capture.

This research is vital for the development of solar thermal power systems. The research delves into the optimization of a tower-based solar thermal power plant’s circular fixed-sun mirror field, with a focus on establishing a spatial coordinate system aligned with the cardinal directions [4]. This study meticulously calculates the positions and the solar angles of heliostat, and direct normal irradiance was used to evaluate the optical efficiency and thermal power output of the mirror field. By integrating these parameters, we aim to determine the annual average thermal power output and its distribution per unit area of the mirror field, thereby enhancing the system’s energy conversion efficiency.

Figure 1. Cartesian coordinate system for spatial mirror field

Figure 1 shows the construction of the spatial mirror field Cartesian coordinate system. A spatial mirror field Cartesian coordinate system is constructed with the due east direction as the x-axis positive direction and the due north direction as the y-axis positive direction. To achieve a rated power output of 60 megawatts, the focus is on researching how to improve the performance of solar thermal power plants. This involves the strategic configuration of absorption towers and heliostats, as well as the mirror dimensions, spacing, and optical efficiency in a multi-dimensional parameter space [5].

In this paper, the particle swarm optimization algorithm [6] is employed to find the most energy-efficient layout, which includes a novel parabolic trough model [7] to minimize shadows and maximize sunlight concentration. Moreover, this algorithm iteratively refines heliostat parameters to maximize the annual thermal power output per unit area, improving the system’s energy capture and conversion efficiency.

2. Construction of model

The angle of solar declination δ can be calculated according to the following equation [8]

\( sin{δ}=sin{\frac{2πD}{365}}sin{(}\frac{2π}{360}×23.45) \) (1)

Depending on the local nodes of time needed to be calculated, the solar time angle ω can be expressed as

\( ω=\frac{π}{12}(ST-12) \) (2)

Assuming the local dimension is 39.4 degrees north, local latitude is denoted by \( φ \) , For ease of calculation, the local latitude-angle system is converted to radians: \( φ=\frac{39.4}{180}π \) . The solar altitude angle \( {α_{s}} \) [9] is characterized by Equation (3)

\( {sin{α}_{s}}=cos{δ}cos{ψ}cos{w}+sin{δ}sin{ψ} \) (3)

According to the changes of date and time nodes different solar altitude angles can be obtained.

Furthermore, the solar azimuth angle \( {γ_{s}} \) [9] can be calculated

\( {cos{γ}_{s}}=\frac{sin{δ}-{sin{α}_{s}}sin{ψ}}{{cos{α}_{s}}cos{ψ}} \) (4)

2.1. Determination of the optimal heliostat arrangement

2.1.1. Solving cosine efficiency \( {η_{cos}} \) : Cosine efficiency is intrinsically linked to the angle of incidence, reflecting the effective sunlight-reflecting area of the heliostat. As the angle increases, the effective area and the corresponding cosine efficiency decrease. According to reference, the direction vector \( \vec{I} \) [10] of the solar incident light can be expressed by its solar motion trajectory

\( \vec{I}({cos{α}_{s}}{sin{γ}_{s}},-{cos{α}_{s}}{cos{γ}_{s}},-{sin{α}_{s}}) \) (5)

For the dimensions of the absorption tower, we know that the height of the solar unit and tower base is 4 metres and the height of the heat absorption tower is 80 metres, the direction vector of the reflected rays from the fixed-heaven mirror’s center point \( ({x_{i}},{y_{i}},{h_{i}}) \) can be derived

\( \vec{R}(-\frac{{x_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},-\frac{{y_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},\frac{H}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}}) \) (6)

Based on this, between angle of solar incidence and the direction vector of the incident solar rays as well as the direction vector of the reflected rays can be established

\( {θ_{s}}=\frac{1}{2}arccos{(}-\vec{I}\cdot {R^{T}}) \) (7)

Combining the above covariates, we can derive a mathematical expression for the cosine efficiency of a fixed-sun mirror [10]

\( {η_{cos}}={cos{θ}_{s}}=cos{(}\frac{1}{2}arccos{(}-\vec{I}\cdot {R^{T}})) \) (8)

2.1.2. Solving atmospheric transmittance \( {η_{at}} \) : The process of calculating the cosine efficiency mediately above is given by the coordinate formula for the distance between two points

\( {d_{HR}}=\sqrt[]{x_{i}^{2}+y_{i}^{2}+(H-h{)^{2}}} \) (9)

In which \( ({x_{i}},{y_{i}},{z_{i}}) \) is the center coordinates of the \( {i_{th}} \) heliostat and H is the height of the heat absorption tower. In addition, atmospheric transmittance is characterised by the following equation [10]

\( {η_{at}}=0.99321-0.0001176{d_{HR}}+1.97×1{0^{-8}}×d_{HR}^{2} \) (10)

In which \( {d_{HR}}≤1000 \)

2.1.3. Solving for shadow masking efficiency \( {η_{sb}} \) :

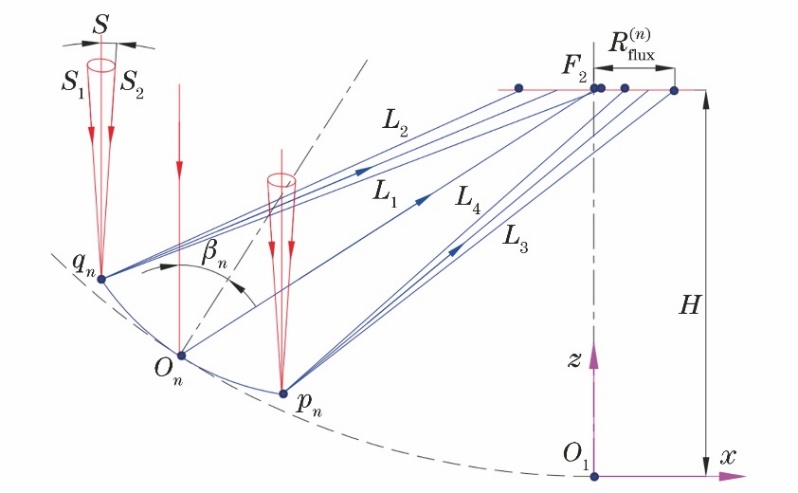
Figure 2. Schematic diagram of solar energy aggregation of mirror unit n in a heliostat field

Figure 2 shows the propagation path of a conical light ray. Assuming that the angle between any ray in the light cone and the principal normal from the center of the sun is \( σ \) and the angle with the \( {X_{s}} \) axis is \( τ \) , the expression for any ray is [10]

\( \vec{{S_{s}}}=(sin{σ}cos{τ},sin{σ}sin{τ},cos{σ}) \) (11)

If all the heliostats are conventional tracking heliostats, the mirror coordinates \( H(x,y,0) \) ,can be transformed into ground coordinates \( {H^{ \prime }} \) [10]

\( H_{1}^{ \prime }=[\begin{matrix}{l_{x}} & {l_{y}} & {l_{z}} \\ {m_{x}} & {m_{y}} & {m_{z}} \\ {n_{x}} & {n_{y}} & {n_{z}} \\ \end{matrix}]\cdot {H_{1}}+{O_{A}}=[\begin{matrix}{{x_{1}}^{ \prime }} \\ {{y_{1}}^{ \prime }} \\ {{z_{1}}^{ \prime }} \\ \end{matrix}] \) (12)

The matrix transformation of the light-cone coordinate system to ground coordinates is given by

\( T=[\begin{matrix}sin{γ} & -sin{α}cos{γ} & cos{α}cos{γ} \\ -cos{γ} & -sin{α}sin{γ} & cos{α}sin{γ} \\ 0 & cos{α} & sin{α} \\ \end{matrix}] \) (13)

If \( \vec{V} \) is a \( {\vec{V}_{s}}=(a,b,c) \) in the light-cone coordinate system, the \( {\vec{V}_{st}} \) [10] is

\( {\vec{V}_{st}}=T\cdot {\vec{V}_{s}}(a,b,c) \) (14)

For the normal vector, we make the fixed heliograph normal unit vector \( {\vec{V}_{N}}=({u_{0}},{v_{0}},{w_{0}}) \) and set the angle between the ray vector \( {\vec{V}_{st}} \) and the normal vector \( \vec{V} \) to \( θ \) , where the cosine of the \( θ \) angle is

\( cos{θ}=\frac{{\vec{V}_{st}}\cdot \vec{{V_{N}}}}{|{\vec{V}_{st}}||\vec{{V_{N}}}|}={\vec{V}_{st}}\cdot \vec{{V_{N}}} \) (15)

The equation of a reflected ray in a light cone is obtained by the geometric structure analysis is

\( \frac{x-{x_{1}}}{m}=\frac{y-{y_{1}}}{n}=\frac{z}{l} \) (16)

The cylindrical surface equation of its collector can be expressed as

\( {x^{2}}+{y^{2}}={R^{2}},Z∈[-\frac{h}{2},\frac{h}{2}] \) (17)

The collector’s light-absorbing capability is evaluated through the intersection of the reflected ray’s equation with the cylinder’s surface. This intersection’s solutions denote absorption, while non-solutions point to shading loss, which is quantified by the non-solution percentage.

2.1.4. Solving for truncation efficiency \( {η_{trunc}} \)

\( \begin{matrix}{η_{trunc}}= & \frac{The collector receives energy}{Specular total reflection of energy-Loss of shadow occlusion} \\ = & \frac{0.92\cdot DNI×6×6}{DNI×6×6-Loss of shadow occlusion×DNI×6×6} \\ = & \frac{0.92}{1-Loss of shadow occlusion} \\ \end{matrix} \) (18)

Then the shadowing occlusion efficiency \( {η_{sb}} \) [10] is

\( {η_{sb}}=1-Loss of shadow occlusion \) (19)

2.1.5. Solve for the fixed-sun mirror field output thermal power E: The obtained \( η \) is brought into the output thermal power of the fixed-sun mirror field [11]

\( {E_{field}}=DNL\cdot \sum _{i}^{N}{A_{i}}{η_{i}} \) (20)

DNI [12] is the normal direct radiation irradiance, \( {A_{i}} \) is the lighting area of the i-th mirror (unit: \( {m^{2}} \) ), \( {η_{i}} \) is the optical efficiency of the i-th mirror, and N is the total number of mirrors(unit : surface).The \( {η_{i}} \) is the optical efficiency of the ith mirror, and N is the total number of solarization mirrors (unit: surface).

2.1.6. Solve for the average thermal power output per unit area of mirror

The average thermal power output per unit area of mirror is given [11]

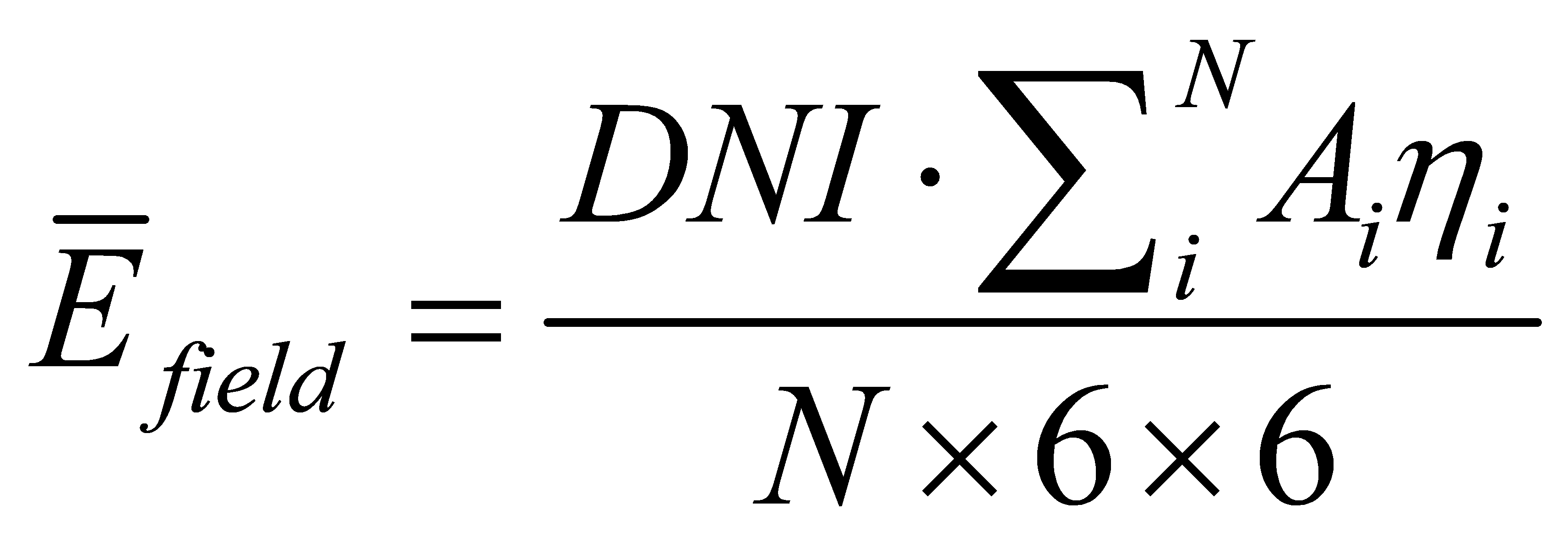(21)

Figure 3. Average optical efficiency and output power for one year

The calculated average optical efficiency and output power for one year are presented in Figure 3 [1,4,13,14]. Solar energy concentration into thermal energy at tower solar thermal power plants is achieved via heliostat mirrors, and which was subsequently transformed into electrical energy. Critical to this process is maximizing the optical efficiency of the mirror field, which involves optimizing the arrangement and positioning of heliostats with the heat absorber. Design considerations encompass the sun’s annual positional variation, the conical nature of sunlight, and balancing heliostat spacing to reduce interference while enhancing land and energy efficiency. Precise alignment of heliostats with the sun, facilitated by advanced tracking technology, is essential for optimal energy capture.

Given the heliostat dimensions \( {l_{1}}×{l_{1}} \) , installation height \( {h_{1}} \) , inter-heliostat spacing \( △x \) , tower height H, and heliostat count N, the objective is to maximize the average annual thermal power output per unit mirror area, subject to various constraints.

Side length constraints for fixed-sun mirrors

\( 2m≤{l_{1}}≤8m \) (22)

Sunset mirror installation height constraints

\( 2m≤{h_{1}}≤6m \) (23)

Distance constraints between neigh boring heliostats

\( △x={l_{1}}+5m \) (24)

Total thermal power constraints on the fixed-sun mirror field

\( E=DNI\cdot \sum _{i}^{N}{A_{i}}{η_{i}} \) (25)

Optical efficiency constraints for heliostats [10]

\( η={η_{sb}}{η_{cos}}{η_{at}}{η_{trunc}}{η_{ref}} \) (26)

Fixed heliograph cosine efficiency constraints

\( {η_{cos}}={{cos_{θs}}}=cos{(\frac{1}{2}arccos{(-\vec{I}×{R^{T}})})} \) (27)

Atmospheric transmittance constraints

\( {η_{at}}=0.99321-0.000176{d_{HR}}+1.97×1{0^{-8}}×d_{HR}^{2} \) (28)

\( {d_{HR}}=\sqrt[]{x_{i}^{2}+y_{i}^{2}+(H-h{)^{2}}} \) (29)

\( {d_{HR}}≤1000 \) (30)

Constraints on the total number of fixed-sun mirrors in the fixed-sun mirror field

\( N=\frac{{P_{e}}\cdot SM}{DNI\cdot S\cdot {η_{1}}{η_{2}}} \) (31)

Where SM is the solar multiplier, take the empirical value of 0.25; S is the area of the heliostat mirror; \( {η_{1}} \) is the empirical efficiency of the heliostat mirror, generally take 63.05%; \( {η_{2}} \) is the empirical efficiency of the rest of the system of the power station, generally take 80.24%. That is

\( N=\frac{{P_{e}}×0.25}{DNI\cdot S×63.05\%×80.24\%} \) (32)

Reflected ray direction vector constraints

\( \vec{R}(-\frac{{x_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},-\frac{{y_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},\frac{H}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}}) \) (33)

Vector constraints on the direction of incident solar rays

\( \vec{I}({cos{α}_{s}}\cdot {sin{γ}_{s}},-{cos{α}_{s}}\cdot {cos{γ}_{s}},-{sin{α}_{s}}) \) (34)

Conditional constraints on the average thermal power output per unit mirror area

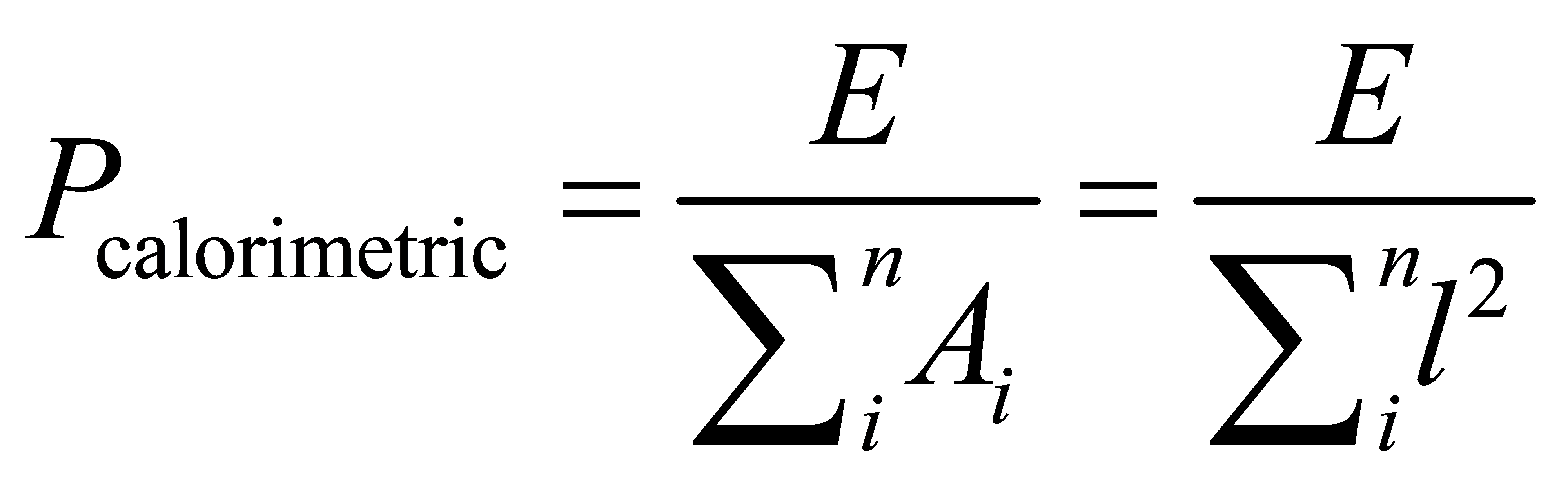(35)

The following optimization is modeled

\( MAX-{\bar{P}_{calorimetric}} \) (36)

Utilizing the particle swarm optimization algorithm, the global optimal configuration of heliostats is determined by iteratively updating their positions and velocities to maximize the annual average thermal power output per unit mirror area, subject to constraints, until the optimal solution is reached.

The study reveals that an optimal fixed-sun mirror distribution is achieved when mirrors are centrally arranged around the heat-absorbing tower with staggered rings, lever-aging the mirror field’s symmetry to simplify optimization through partitioned analysis and iterative local arrangement, ultimately obtaining the best heliostat layout for the entire field. The optimization results are used to obtain the optimal heliostat arrangement for the whole mirror field by using the symmetric geometrical characteristics as shown in Figure. 4.

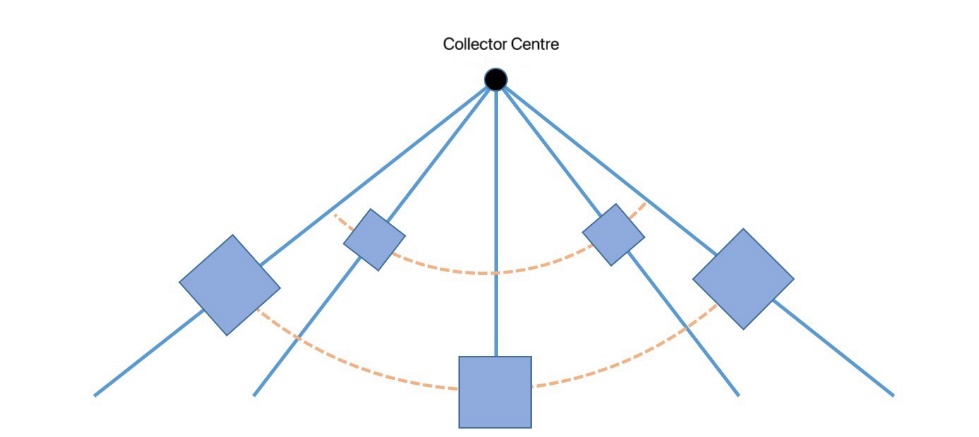
Figure 4. Optimal distribution for the same mounting height of the heliostat

The average optical efficiency and output power for the two-year problem are shown in the Figure 5

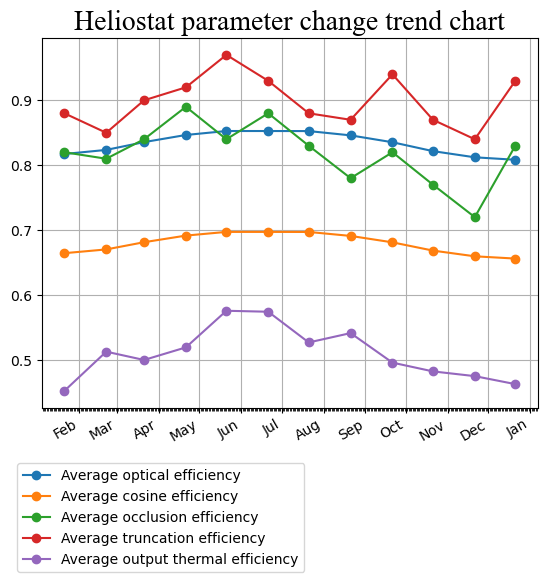
Figure 5. Average optical efficiency and output power for two years

2.2. Optimal Output Thermal Power of Heliostat-Based on Different Mounting Heights

Building upon the Problem, introduces variable heliostat sizes and mounting heights, leveraging the parabolic trough reflective mirror arrangement to minimize shadow loss. The optimal focal length for the parabolic trough reflector surface is determined to be \( f=\frac{R}{2} \) , resulting in the best heat collection at the position \( (0,0,40m) \) , with the parabolic equation given by \( {x^{2}}=4fz \) .

Involving the division and rotation of mirror units symmetrically around a central point, the optimization process defines parameters such as mirror area, installation height, and tower height. It sets the objective to maximize the average annual thermal power output per unit mirror area, adhering to specific constraints. These constraints include

Side length constraints for fixed-sun mirrors

\( 2m≤{l_{1}}≤8m \) (37)

Sunset mirror installation height constraints

\( 2m≤{h_{1}}≤6m \) (38)

Distance constraints between neigh boring heliostats

\( △x={l_{1}}+5m \) (39)

Total thermal power constraints on the fixed-sun mirror field

\( E=DNI\cdot \sum _{i}^{N}{A_{i}}{η_{i}} \) (40)

Optical efficiency constraints for heliostats (0 shadow masking efficiency)

\( η={η_{cos}}{η_{at}}{η_{trunc}}{η_{ref}} \) (41)

Fixed heliograph cosine efficiency constraints

\( {η_{cos}}={{cos_{θs}}}=cos{(\frac{1}{2}arccos{(-\vec{I}×{R^{T}})})} \) (42)

Atmospheric transmittance constraints

\( {η_{at}}=0.99321-0.000176{d_{HR}}+1.97×1{0^{-8}}×d_{HR}^{2} \) (43)

\( {d_{HR}}=\sqrt[]{x_{i}^{2}+y_{i}^{2}+(H-{h_{i}}{)^{2}}} \) (44)

\( {d_{HR}}≤1000 \) (45)

Constraints on the total number of fixed-sun mirrors in the fixed-sun mirror field

\( N=\frac{{P_{e}}\cdot SM}{DNI\cdot A\cdot {η_{1}}{η_{2}}} \) (46)

Where SM is the solar multiplier, take the empirical value of 0.25; A is the mirror area of the heliostat; \( {η_{1}} \) is the empirical efficiency of the heliostat, generally take 63.05%; \( {η_{2}} \) is the empirical efficiency of the rest of the system of the power station, generally take 80.24%. That is

\( N=\frac{{P_{e}}×0.25}{DNI\cdot A×63.05\%×80.24\%} \) (47)

Reflected ray direction vector constraints

\( \vec{R}(-\frac{{x_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},-\frac{{y_{i}}}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}},\frac{H}{\sqrt[]{x_{i}^{2}+y_{i}^{2}+{H^{2}}}}) \) (48)

Vector constraints on the direction of incident solar rays

\( \vec{I}({cos{α}_{s}}\cdot {sin{γ}_{s}},-{cos{α}_{s}}\cdot {cos{γ}_{s}},-{sin{α}_{s}}) \) (49)

Conditional constraints on the average thermal power output per unit mirror area

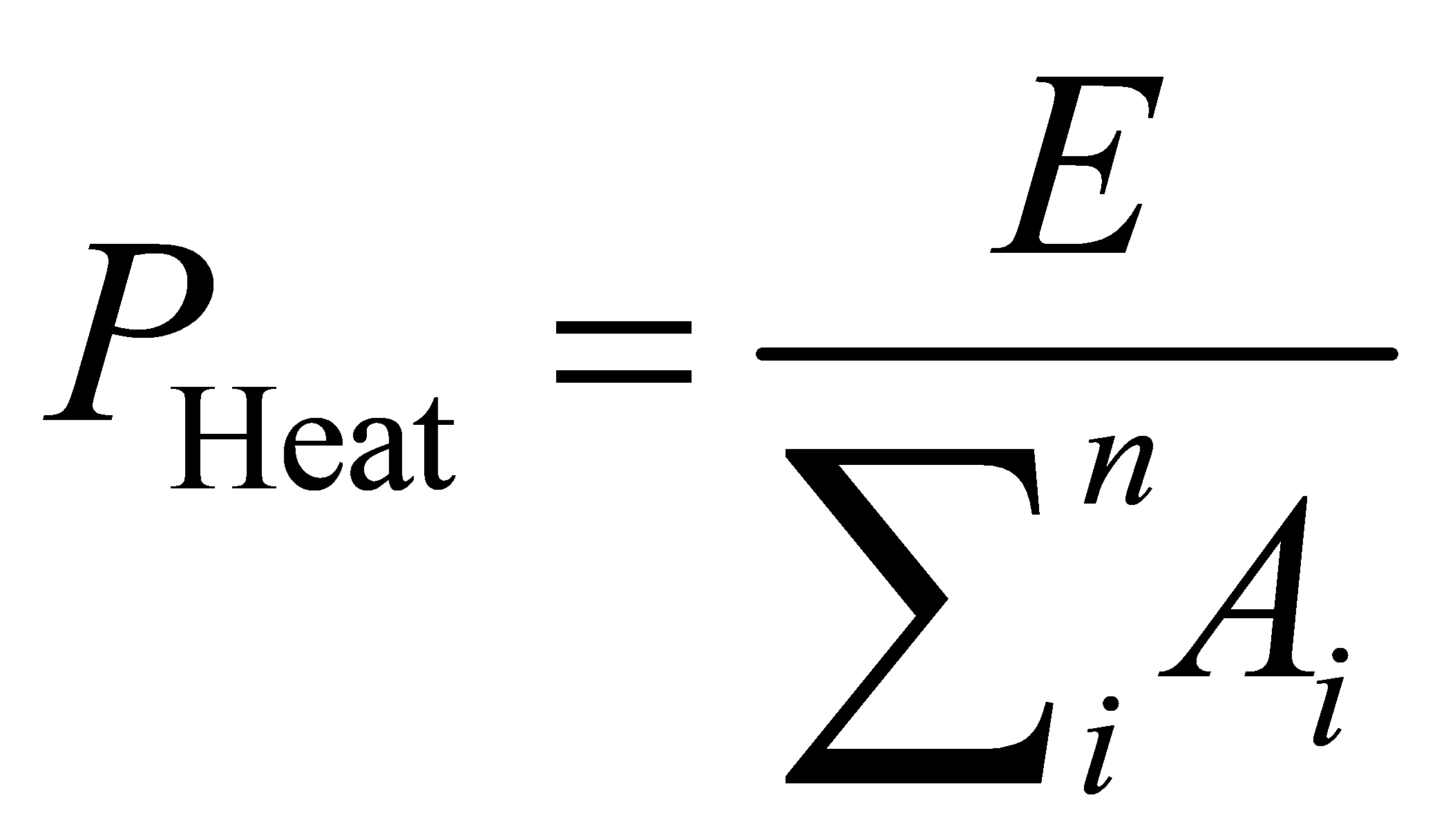(50)

Constraints on the equations of the parabolic bus

\( x_{i}^{2}=4f{z_{i}} \) (51)

Optimal focal length taking constraints

\( f=\frac{R}{2}=40m \) (52)

Solar time angle \( ω \) bound

\( ω=\frac{π}{12}(ST-12) \) (53)

Solar declination angle \( δ \) constraint

\( sin{δ}=sin{\frac{2πD}{365}}sin{(}\frac{2π}{360}×23.45) \) (54)

Solar altitude angle \( {α_{s}} \) constraint

\( {sin{α}_{s}}=cos{δ}cos{ψ}cos{w}+sin{δ}sin{ψ} \) (55)

Solar azimuth \( {γ_{s}} \) constraint

\( {cos{γ}_{s}}=\frac{sin{δ}-{sin{α}_{s}}sin{ψ}}{{cos{α}_{s}}cos{ψ}} \) (56)

In summary, an optimization model is developed.

3. Conclusion

In this paper, the particle swarm algorithm (PSO) combined with analytical geometry and matrix transformation methods is used to develop a mathematical model for multi-objective planning to optimize the design of a heliostat mirror field in a tower solar thermal power plant. The study focuses on adjusting the size, mounting height, and arrangement of the heliostat mirrors to maximize the annual average output thermal power per unit mirror area while satisfying a series of constraints such as optical efficiency, atmospheric transmittance, and shadow shading efficiency. The model not only takes into account the angle of incidence and reflection of sunlight, but also the interference between heliostats and the land use efficiency, aiming to achieve the optimal design of the heliostat field, to improve the efficiency of solar energy utilization, to reduce the cost, and to promote the development and application of related technologies. Analytical geometry and matrix modeling resulted in average annual efficiencies: optical (0.7338), cosine (0.6797), shading (0.8775), and truncation (0.8983), with a 294.6007 MW thermal output and 0.3908 MW/sq m. A multi-objective model, using a particle swarm algorithm, optimized heliostat arrangement, achieving a circular configuration around the tower at (0,0,80m), with 2650 heliostats over 9540 sq m of reflectivity covering 55656 sq m.

Acknowledgments

This work was financially supported by the Fundamental Research Funds for the Inner Mongolia Normal University (Grant No. 2023JBYJ016). Lei Li would like to acknowledge the financial support from the research support project of introducing high-level talents.