1 Introduction

The birth of chaos theory has made it possible to predict future chaos, allowing humans to obtain a general direction of the future. Nonlinear dynamic chaos can evolve based on initial conditions and external changes. Fractals theory, on the other hand, studies objective phenomena through observations from different dimensions or using various mathematical methods.

In the Nonlinear Dynamic Chaos of Tong Wu, he summarizes the definition of this theory and provides detailed classifications, including temporal and spatial chaos, complete and limited chaos, and strong and weak chaos. His article discusses the characteristics of chaos, methods for identifying chaos, and signs of chaos, distinguishing between chaos and noise. It also explores the epistemological and methodological significance of chaos theory in four aspects, for example, the significance of chaos research for the nonlinear methodology in complexity studies, the relationship between chaos and determinism and predictability, the significance of chaos edge research, and the relationship between construction and avoidance of chaos [1].

Regarding the fractals theory, which also possesses chaotic properties, Zhang Jun introduces the concept of dimension in The Beauty of Mathematical Chaos—A Preliminary Understanding of Fractal Geometry through the French mathematician Benoit Mandelbrot's paper published in the American journal Science and the Koch curve considered by H. von Koch in 1904. Dimension is an essential characteristic of fractal geometry [2].

This article summarizes and compares these two theories. It outlines the theories of chaos and fractals and their applications in people’s daily life, providing reference value for beginners and new research ideas for future researchers.

2 The development of chaos theory

In the past, computer experiments were the primary method for scientists to study chaos. However, after the 1980s, the focus of research shifted from the behavior of chaos to its structure. Peter Grassberger, H. George E. Hentschel, and Itamar Procaccia proposed theories and methods for reconstructing dynamical systems, which freed chaos theory from the constraints of theoretical model research and accelerated its application to real-world scenarios.

2.1 Core concepts of chaos theory

There are many definitions of nonlinear dynamical chaos. Norman Packard describes chaotic phenomena as the butterfly effect, sensitivity to initial conditions, and information proliferation. In determinism, random behavior may exist, which is a specific attribute of chaos. Small differences in initial states can lead to significantly different outcomes, and these small differences become larger as the system evolves [3]. In China, there are various perspectives on this theory, but two points of consensus exist: first, chaos is an apparently random, non-periodic behavior that can be generated by deterministic processes; and nonlinear problems cannot be treated as simple linear problems. In summary, chaotic behavior is simple but unpredictable. In determinism, chaos can greatly influence results, where small changes cause large differences. The discovery of nonlinear dynamical chaos has significantly helped scientists study chaos in terms of spatial dimensions, but so far, this theory remains limited to low-dimensional ordinary differential equations or difference equations.

2.2 The significance of chaos

Chaos theory has many implications. It challenges traditional views and refutes the notion that "simple systems lead to simple behavior, and complex systems produce complex behavior." It shows that simple systems can generate complex chaotic behavior through simple rules, and complex systems can also produce simple behavior.

Chaos theory has also promoted the evolution of methodology. Before the advent of chaos theory, scientific research mainly focused on linear research, using methods such as reducing high-level phenomena to low-level ones or summing up low-level phenomena to derive high-level ones. However, after the introduction of chaos theory, the focus shifted from linear to nonlinear research, and scientists began to adopt a more holistic approach to their studies.

Endogeneity and Nonlinearity. Chaos is inherent to a system and not caused by external forces. The endogeneity of chaos does not stem from hidden internal forces but from the system's nonlinear structure and internal interactions.

The methodological revolution has revealed the complexity of simple systems, forcing people to be prepared to handle complex behaviors even when dealing with simple systems. This methodological shift emphasizes the idea of "treating and handling nonlinearity as nonlinearity."

Determinism and Randomness. Chaos appears to be a random state, but its emergence is not due to randomness; it is the result of a deterministic system. Chaos theory extends the scope of determinism, emphasizing that even within a deterministic framework, complex behavior and unpredictability still exist.

The theory provides the potential for prediction. Chaos theory offers a new perspective on the possibility of prediction, stating that predicting strong chaos or complete chaos is impossible, whereas predicting weak chaos is possible, which reflects a challenge to traditional linear prediction methods and a reexamination of epistemological views on cognosciblism and agnosticism.

3 Fractal Geometry

3.1 Self-similarity

The basic characteristic of fractal geometry is that fractal patterns are created by proportionally scaling down and replicating themselves, resulting in local and overall similarity. The fundamental principle of it is self-similarity. Self-similarity refers to the property of a fractal object where its enlarged parts resemble the whole. This theory can be divided into three types.

First, it has exact self-similarity, such as the Sierpiński triangle, which is a large triangle composed of many smaller triangles that are identical in structure but different in scale. This similarity is very precise.

Second, it has approximate self-similarity, also called semi-self-similarity, which means that within a certain range, the overall structure is similar but not exactly the same, and the internal details differ. For example, if you continuously zoom in on a tree, the structure at each level of magnification is similar, but the distribution of leaves and branches varies.

Third, it has statistical self-similarity, where the similarity is not apparent in the overall structure but is similar in a statistical sense.

3.2 Fractal dimension

To study fractal geometry, dimensions are essential, with the Hausdorff dimension being both traditional and most important. The Hausdorff dimension, often denoted as \( dim_{H} \) , differs from the conventional Euclidean dimension. Euclidean dimensions are used for studying integer dimensions, while the Hausdorff dimension is applied to complex, non-integer fractal structures [4]. The Hausdorff dimension also satisfies several properties, such as monotonicity, countable stability, countable set, open set, and smooth set. Its most fundamental property is that the Hausdorff dimension is invariant under bi-Lipschitz transformations.

4 The application of chaos and fractals

4.1 Chaos and fractals in the nature

Chaos and fractals also exist in the nature. Snowflakes and leaves are well-known examples of fractal geometric shapes, as shown in Figure 1 and Figure 2. When magnified, their parts resemble the whole, making them examples of precise self-similar fractals. Not only snowflakes and leaves, but also rocks and brain waves exhibit fractal properties. Although rock surfaces are rough, their variations can be described using dimensions, which is of great significance in geography. Brain waves also utilize dimensions, and it has been found that fractal dimensions can predict epilepsy, playing a crucial role in the treatment of epilepsy patients. In the past, some unobservable phenomena were considered chaotic, but from the fractal perspective, these phenomena are neither random nor disordered. They can even be predicted and controlled.

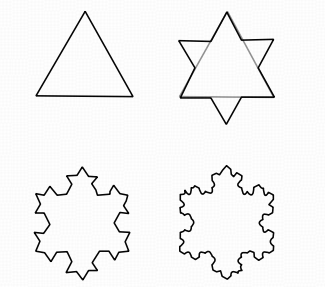
Figure 1. The snowflake [5]

Figure 2. The Barnsley fern [5]

4.2 Other applications

Fractals can be integrated with many disciplines. When combined with computer science, it has given rise to a new field of study, which has seen extensive researches and applications, yielding significant results. In 1989, A.E. Jacquin proposed the fundamental block-based fractal image compression encoding method. This method has been continuously improved and is now used in fractal compression software [6]. When integrated with fluid mechanics, scientists use chaos theory to study the laws of turbulent motion. Some have provided chaotic motion trajectories observed in real physical spaces. Chaos theory is also expected to be introduced into the field of seepage, an important branch of fluid mechanics. Using chaos theory, researchers can study complex seepage systems, transforming seemingly disordered gases and liquids into observable forms in a fractal state [7].

4.3 Challenges and future development

Although chaos theory and fractal geometry have been widely used in many scientific fields and have achieved fruitful research results, they still face some important challenges. First, for many complex systems, it is still difficult to accurately characterize their dynamic behavior. Chaotic systems are often highly sensitive to initial conditions, and even small disturbances can lead to huge differences in system evolution, which poses great challenges to prediction and control. At the same time, there are certain difficulties in the accurate measurement of fractal structures, especially under the influence of factors such as noise interference and boundary effects. Secondly, chaos and fractal theory have also encountered some bottlenecks at the application level. For example, in the field of economics and finance, how to use these theories to better predict market fluctuations and avoid risks is still a thorny problem. In medical diagnosis, how to apply chaos theory to early warning of complex diseases such as arrhythmia and cancer also needs to be broken through. In addition, the mathematical foundation of chaos and fractals still needs to be further improved and perfected. The rigorous proof of some key concepts and theorems, as well as the in-depth integration with other branches of mathematics, require the unremitting efforts of mathematicians.

Looking into the future, chaos theory and fractal geometry will surely achieve new breakthroughs and developments in various aspects. In terms of theoretical innovation, scientists will continue to explore new models of complex system behavior and propose more accurate description and prediction methods. In terms of interdisciplinary applications, chaos and fractals will further penetrate into a wider range of fields such as physics, biology, and economics, and promote the innovative development of related disciplines. In terms of computing technology, with the help of emerging technologies such as artificial intelligence and big data, the simulation and analysis of chaos and fractal models will surely achieve a qualitative leap. In terms of education and teaching, chaos theory and fractal geometry, as important components of modern science, will surely become the focus of natural science education.

5 Conclusion

Chaos theory and fractal geometry are in a critical period of rapid development. They will play an increasingly important role in understanding the nature and solving practical problems. Through the unremitting exploration of scientists, these two theories will bring more imaginative discoveries and inject new impetus into the depth and breadth of human cognition of the world.

This paper mainly uses the method of literature review to summarize the conclusions given by predecessors and briefly introduces the development and significance of fractal and chaos theory. At the same time, the limitations of these theories and the challenges they face are analyzed. By reviewing the core concepts, mathematical principles and specific practices of these two theories in different disciplines, it is hoped that readers will have a better understanding of the behavior of complex systems and look forward to the future development trend of chaos and fractal theory. This will help to further promote the application and innovation of these theories in scientific research and practical applications, and provide new ideas for theoretical development.

Although this paper summarizes the origin, development and properties of chaos fractal theory, it has not conducted in-depth scientific research on it, and has not used mathematical methods to study chaos fractal theory.

Chaos and fractals may be difficult to understand, and many phenomena may be difficult to explain. But this is a new discipline, as long as continue to study it in depth, people will definitely gain something.