1. Introduction

With the development of the economy, people’s living standards have been improving gradually, and their happiness index has been increasing continuously. To facilitate travel, cars have become an essential part of people’s daily lives [1]. However, high purchase costs for new cars and rapid depreciation have always troubled consumers. Consequently, more and more consumers are turning to the second-hand car market, seeking more cost-effective car buying options. In the United States, for example, second-hand cars are traded at roughly three times the rate of new cars [2]. Against this backdrop, the trading volume of the second-hand car market is gradually increasing, and the importance of predicting second-hand car prices is becoming increasingly prominent.

The volatility of the second-hand car market brings significant uncertainty to both sellers and buyers, with various factors influencing second-hand car prices to varying degrees. Wang researched the different degree effects of vehicle age, power, mileage, model and other factors on the price [3]. In reality, buyers might fear purchasing vehicles with low value at high prices, while sellers worry that their vehicles may not fetch reasonable prices [4]. This uncertainty not only affects the market’s trading efficiency but also constrains its healthy development. Therefore, establishing a scientific price prediction model for second-hand cars is crucial in reducing market uncertainty and enhancing trading efficiency.

Research on old car price prediction can enhance market efficiency and promote its healthy development [5]. By predicting second-hand car prices, consumers and car dealers can grasp market dynamics more accurately, thus making more rational decisions. Moreover, second-hand car prediction is conducive to stabilize market prices, prevent excessive price fluctuations, and maintains a level playing field in the market. Finally, predicting second-hand car prices is beneficial to avoid negotiations and disputes caused by unreasonable prices between consumers and car dealers. This reduces transaction costs and improves the overall efficiency of the market.

There are multiple methods and models to predict the price of second-hand cars. This paper tries to put the influencing factors of second-hand car prices under the test of objective data. Linear regression is a classical method in statistics. With the advent of the era of big data, machine learning algorithms have been studied and applied by more people. Zhu used several machine learning models and neural network models to predict the price of second-hand cars [6]. Zheng and others analyzed and compared the multiple linear regression model and the neural network model [7]. Zhu and Zheng concluded that neural network predictions have more accurate results for respective research problems. Jia built a model based on the Light Gradient Boosting Machine (GMB) algorithm and analyzed and compared it with other algorithms in machine learning to get the advantages of Light GMB [8]. Chetna and other researches compared the random forest algorithm with the e Xtreme gradient boosting algorithm through the integration technique. Finally, it is concluded that the e Xtreme boost algorithm is better [9]. Chen and his companions studied the different advantages of random forest and linear regression models in different situations, and random forest is better for dealing with complex models [10]. This paper mainly uses the linear regression method and random forest model to solve this problem and test the model effect. Preprocessing the data and performing descriptive statistics. This article will explore the relationship between second-hand price and vehicle condition. Because there are categorical variables in the independent, this article chooses to use dummy variable regression. In addition, this paper will also study random forest models to comprehensively analysis to solve this regression problem.

2. Methodology

2.1. Data source and description

The data for this article comes from the Kaggle website and has been updated by Milan Vaddoriya. There are a total of 5513 samples, 8 influencing factors and 1 dependent variable--car price.

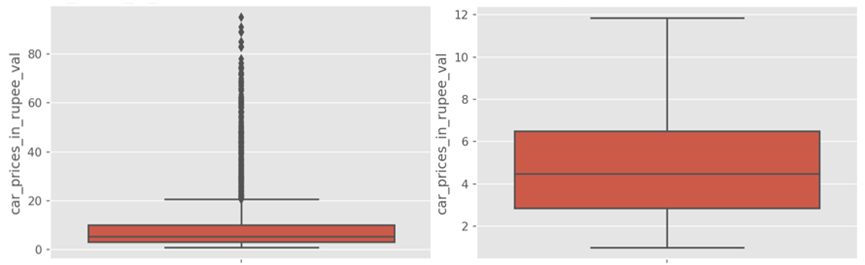
Figure 1. Car price in rupee (Lakh) before and after removing outliers

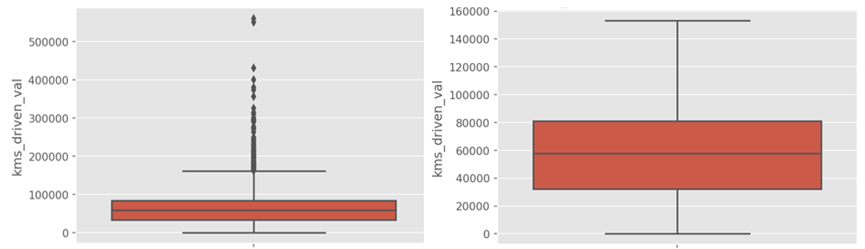
Figure 2. Kilometers driven before and after removing outliers

It can be seen from the box plot (Figure 1, 2) that there are too large values in the car price and kilometers traveled in the data, which not be conducive to the accuracy of the model. Therefore, these outliers are deleted. Now there are 4032 samples.

2.2. Index selection and description

Independent variables include fuel type, transmission type, ownership, seats, kilometers driven, manufacture year, engine capacity and car name. Ownership means the number of transfers, and the number of seats represents the size of the car. According to the objective phenomenon, the second-hand car brand is positively correlated with the price. In other words, the better the brand, the higher the price. However, car brands are used as categorical data, which cannot be assigned a specific value. Therefore, this variable will not be analyzed and further discussed for the following models.

To make the data better for modeling, it is necessary to analyze the data further. There are categorical variables and numeric variables in the influencing factors of second-hand car prices (Table 1). Although the year of manufacturing and the number of transfers is usually treated as discrete variables, to describe the effect of their changes on dependent variables, they are quantified as continuous variables and applied in mathematical methods. The significance of this is to describe their trends, not their numbers themselves.

Table 1. Variable description.

2.3. Method introduction

2.3.1. Multiple linear regression

Because there are categorical variables (transmission type, fuel type, seats) in the independent variables, the multiple linear regression analysis cannot be carried out directly. Therefore, it is necessary to use dummy variables and then carry out general linear regression. Dummy variables are created using petrol, automatic and ownership=5 as reference groups.

\( {y_{i}}={β_{0}}+{β_{1}}{x_{1}}+{β_{2}}{x_{2}}+…+{β_{i}}{x_{i}}+{ε_{i}}\ \ \ (1) \)

2.3.2. Random forest

Random forest is an integrated learning algorithm based on decision trees, which can be used to solve regression problems. Random forest has good accuracy and stability. In the study of the factors affecting the price of second-hand cars, 90% of the data is used as a training set, and 10% is used as a test. Data normalization is used to train the data, and parameters are adjusted to find the optimal model.

3. Results and discussion

3.1. Descriptive statistics

There are five fuel types, mainly diesel and petrol, which far outnumber the other three. The number of second-hand petrol cars is almost 2500, and the number for diesel is about 1500. The number of second-hand cars of CNG, electric and LPG types is less than 100 (Figure 3).

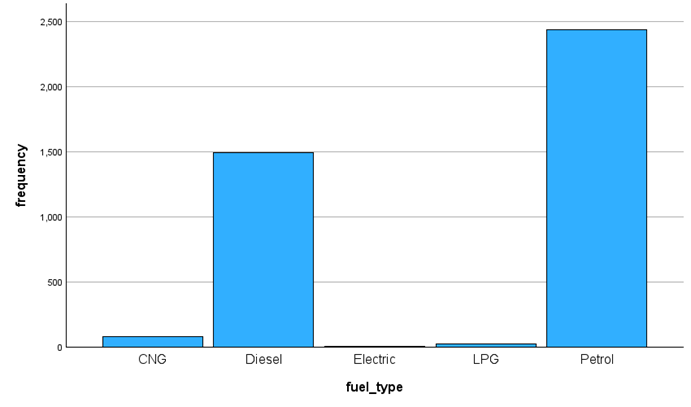
Figure 3. Bar Plot of Fuel Types

It can be seen that most of the cars in this data set are manual transmission cars. There are about seven times as many manual cars as automatic cars. The number of manual cars is about 3500, and the number of automatic cars is about 500 (Figure 4).

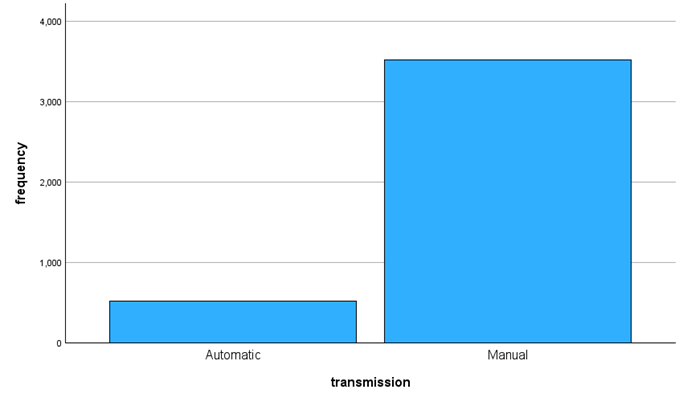
Figure 4. Bar Plot of Transmission Type

The manufacturing years of the cars in the data are mainly concentrated between 2010 and 2020. The most cars were produced in 2017, with nearly 500. Few cars were produced in the years before 2009, less than 100 cars a year (Figure 5).

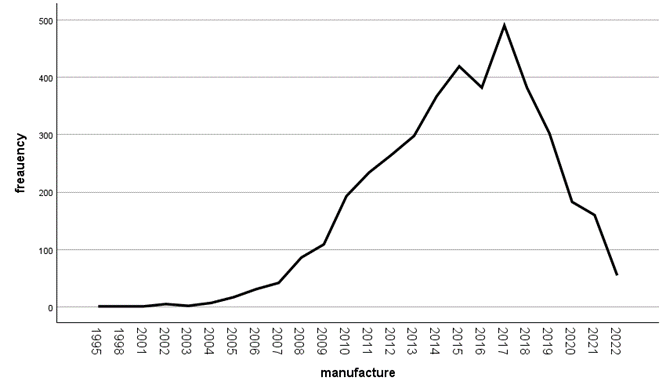
Figure 5. Line Plot of Car Counts by Manufacture Year

As can be seen from the figure, fuel type has a certain impact on second-hand car prices. The average price of second-hand cars of diesel type is the highest, and that of LPG is the lowest (Figure 6).

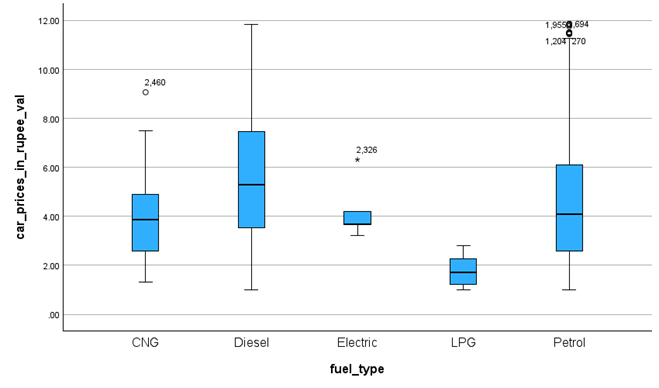
Figure 6. Box Plot of Fuel Type

The price of second-hand cars with automatic transmission is generally higher than manual transmission second-hand cars. The average price of a second-hand car with an automatic transmission is about 3 Lakh more expensive than a manual transmission (Figure 7).

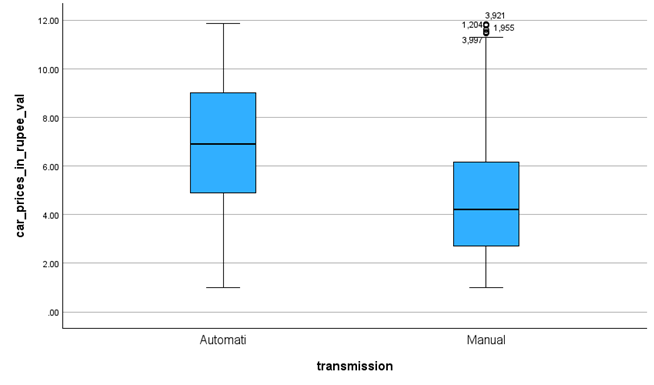
Figure 7. Box Plot of Transmission Type

The number of transfers is negatively correlated with the mean value of the car price. Within three transfers, the price decreases significantly with the increase in the number of transfers (Figure 8).

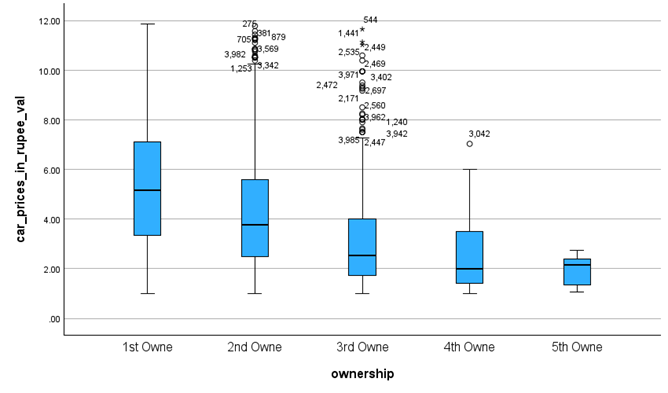
Figure 8. Box Plot of Ownership

There are 85.66% of second-hand cars are five-seater, accounting for the largest proportion. Followed by seven seats, and the proportion of other seats is seldom. The smallest number is the two-seater, with only four cars (Figure 9).

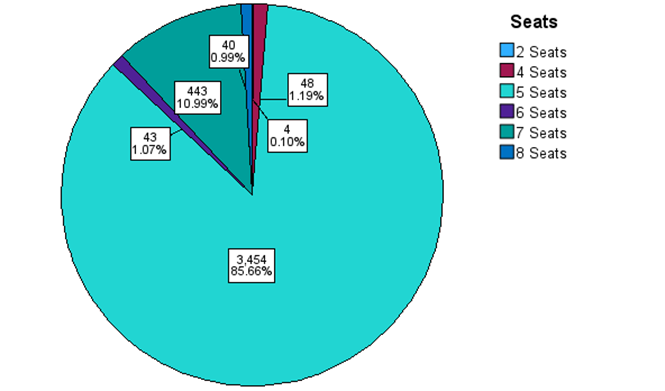
Figure 9. Pie Chart of Seats

3.2. Correlation analysis

This can be seen from Figure 10, the car price is positively correlated with the year of manufacture and is not significantly positively correlated with engine displacement and number of seats, negatively correlated with the number of kilometers driven and ownership. The number of kilometers traveled is positively correlated with the year of production and the number of transfers. There is a negative correlation between the year of production and the number of transfers. In addition, there is no obvious linear correlation between the other variables.

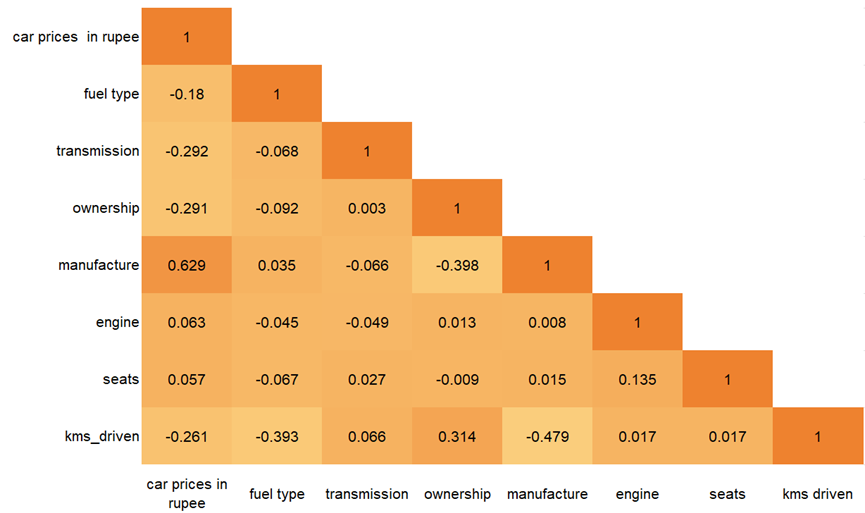
Figure 10. Pearson correlation

3.3. Multiple linear regression model results

From Table 2, note that VIF is much less than 5, and there is no multicollinearity between the independent variables. The model can be carried out accurately, and the parameter estimation is more reliable and accurate. As can be seen from Table 3, kms driven, transmission, fuel type, manufacture, and ownership have a significant impact on the dependent variable second-hand car price.

Table 2. Linear Model Coefficient

The prediction value of second-hand:

\( car({x_{1}})=-801.804-(4.498E-6){x_{2}}-…+2.041transmission2manual+ε\ \ \ (2) \)

However, there are some non-significant variables here that require further simplification of the model. A new linear regression model is obtained without considering the effect of seat number on price (Table 3).

Table 3. Simplified model parameters

The regression equation after the simplified model is:

\( car({x_{1}})=-803.901-(4.493E-6){x_{2}}-2.040transmission2manual-…+ε\ \ \ (3) \)

Table 4. Model summary

\( SE=\sqrt[]{\frac{SSE}{n-k-1}}=1.7545\ \ \ (4) \)

The smaller the SE, the better the representation of the regression line to each observation point (Table 4). R² measures the degree of fitting of the model to the data.

\( {R^{2}}=\frac{SSR}{SST}\ \ \ (5) \)

The closer the model is to 1, the better the fitting effect is. \( {R^{2}} \) is equal to 0.536. Avoid overfitting the adjusted value \( R_{a}^{2}=0.535 \) . The model has a certain interpretability, but it does not have a high degree of fit.

3.4. Random forest model results

Of these factors, the most influential is manufacture year (58.79%), followed by kilometers driven (10.63%), the type of fuel and the transmission type, and the engine displacement, and finally the number of transfers and the number of seats (Table 5, 6).

Table 5. Characteristic weight value

Table 6. Model evaluation

For test set,

\( SSE=MSE*n=2.595*4032=10463.04\ \ \ (6) \)

The sum of squares of error between the predicted value and the observed value is 10463.04. \( {R^{2}}=0.602 \) . This means that the independent variables can explain 60.2% dependent variables.

3.5. Discussion

In the multiple linear regression model, \( SSE=13080.80. \) SSE is directly related to the model quality, the smaller its value, the higher the model fitting accuracy. The SSE in the multiple linear regression model is 1.19 times that of the test data in the random forest model. And the R-square in the random forest is greater than the R-square value in the linear regression model. The random forest model has a better fitting effect and accuracy than the regression model.

4. Conclusion

Compared with the multiple linear regression model, the random forest model can better predict second-hand car prices, the fitting effect of this model is better, and the error is relatively small. Among these factors, the year of production of a car has the greatest impact on the price of second-hand cars. For multiple linear regression models, some independent variables may not have linear effects on dependent variables, or the linear relationship between them is not obvious. These independent variables may include but are not limited to fuel type, and transmission type. This situation may lead to increased errors, which is a limitation of a linear regression model. Due to the excessive complexity of car names, this variable is not introduced into the model, and other factors not mentioned in the data affect second-hand car prices, which also leads to a decrease in the accuracy of the fit. The number of car accidents, car color and geographical location factors have a certain impact on the price of second-hand cars. If more factors are taken into account, the model will work better. This can be seen in the model results, the year of production is an important factor in the price of a second-hand car, while the number of seats and most fuel types have little effect on the price.