1. Introduction

Supply chain management is a critical function for organizations seeking to enhance efficiency and competitiveness. As global markets become more interconnected, optimizing supply chain networks presents both opportunities and challenges. Traditional linear programming (LP) techniques provide a foundation for addressing these challenges but often fall short when decision variables must be whole numbers. This necessity introduces Mixed Integer Linear Programming (MILP), a sophisticated approach that incorporates integer variables to reflect real-world constraints such as the number of production batches or transportation trips. MILP transforms the optimization landscape by making the solution space discrete and non-convex, requiring specialized algorithms like branch-and-bound and branch-and-cut to navigate this complexity. These advanced techniques enable efficient exploration of large solution spaces, identifying optimal solutions that meet all constraints. For example, in a transportation problem, the need to minimize the number of trips while ensuring timely deliveries requires integer solutions, as fractional trips are impractical. The application of MILP extends across various industries, from retail and manufacturing to pharmaceuticals, each with unique supply chain dynamics. In retail, optimizing warehouse locations and inventory levels can significantly reduce transportation costs and improve service levels [1]. Manufacturing firms leverage MILP to enhance production schedules and distribution routes, achieving cost savings and reduced lead times. Pharmaceutical companies use MILP to ensure regulatory compliance and timely delivery of medications, crucial for patient care. This paper delves into the theoretical underpinnings of MILP, explores its application in supply chain optimization, and presents case studies to illustrate its practical benefits. By examining these aspects, we aim to highlight the transformative impact of MILP on supply chain management, offering insights for businesses looking to optimize their operations in an increasingly complex and competitive landscape.

2. Theoretical Foundations of MILP

2.1. Linear Programming Basics

Linear programming (LP) is a fundamental technique in optimization used to achieve the best outcome, such as minimizing costs or maximizing profits, given a set of linear constraints. The general form of an LP problem consists of an objective function and a set of constraints. The objective function, typically a linear equation, represents the goal of the optimization, such as minimizing the total cost in a supply chain network. Constraints, on the other hand, represent the limitations or requirements of the system, such as production capacities, demand requirements, or budgetary restrictions.

For example, consider a company that produces two products, A and B. The objective function might be to maximize the total profit, represented as Z=50x1+40x2, where x1and x2 are the quantities of products A and B, respectively. The constraints might include limitations on labor and material, such as 2x1+3x2≤120(labor hours) and x1+2x2≤100(material units) [2].

To solve LP problems, algorithms like the Simplex method are commonly used. The Simplex method iteratively moves along the edges of the feasible region defined by the constraints to find the optimal solution. This method is efficient for many practical problems and can handle a large number of variables and constraints. For instance, in a supply chain optimization problem with hundreds of products and multiple constraints, the Simplex method can quickly navigate through the feasible region to identify the optimal distribution of resources, minimizing overall costs while meeting all demand requirements.

2.2. Introduction to Integer Variables

In many real-world applications, decision variables cannot be fractional and must take on whole numbers. For example, when determining the number of trucks to dispatch or the number of production batches to run, fractional values are not practical. This requirement introduces integer variables into the optimization problem, transforming it into a Mixed Integer Linear Programming (MILP) problem.

The inclusion of integer variables adds significant complexity to the problem because the solution space becomes discrete and non-convex. This means that traditional LP solution techniques, which rely on convexity, are no longer applicable. For instance, in a transportation problem where the goal is to minimize the number of trips while ensuring all deliveries are made, the number of trips must be an integer. A fractional trip does not make sense in this context [3].

The complexity arises because the number of possible solutions increases exponentially with the number of integer variables. Consider a supply chain problem with five potential warehouse locations (binary decision variables for each location: open or closed). The solution space consists of 2⁵=32possible combinations. As the number of decision variables grows, this space becomes vast, making the problem challenging to solve. Specialized algorithms and techniques, such as branch-and-bound, are necessary to efficiently explore this large and complex solution space to find the optimal integer solution. Table 1 illustrates the concept of integer variables in an MILP problem, using the example of deciding whether to open or close five potential warehouse locations.

Table 1. Integer Variables In MILP

2.3. MILP Solution Techniques

Solving MILP problems involves advanced techniques that efficiently navigate the discrete and non-convex solution space. One widely used method is the branch-and-bound algorithm. This technique systematically explores branches of the solution space tree, calculating bounds to eliminate regions that do not contain the optimal solution. For example, in a production scheduling problem with constraints on machine capacities and delivery deadlines, branch-and-bound can effectively prune suboptimal schedules, focusing computational efforts on the most promising regions of the solution space. Another powerful method is the branch-and-cut algorithm, which enhances branch-and-bound by incorporating cutting planes. Cutting planes are linear inequalities added to the MILP model to exclude infeasible regions without excluding any feasible integer solutions. This technique refines the feasible region iteratively, converging towards the optimal solution more quickly. For instance, in a logistics network design problem, cutting planes can eliminate infeasible routes, reducing the complexity and solving time of the problem. Modern MILP solvers, such as CPLEX and Gurobi, implement these advanced techniques efficiently [4]. These solvers are equipped with sophisticated algorithms that handle large-scale MILP problems involving thousands of variables and constraints. For example, Gurobi's parallel processing capabilities can solve complex optimization problems in industries ranging from energy to finance within reasonable timeframes. Additionally, these solvers incorporate heuristic methods to quickly find good feasible solutions, which are then refined through exact optimization techniques. In a supply chain context, a heuristic might provide a near-optimal initial solution for warehouse placement, which the solver then improves upon, ensuring that the final solution is both optimal and computationally feasible.

3. Modeling Supply Chain Networks with MILP

3.1. Network Design

Designing a supply chain network involves making critical decisions regarding the optimal locations and capacities of various facilities, such as plants, warehouses, and distribution centers. MILP models for network design are constructed to address these decisions by including decision variables that represent facility locations, production quantities, transportation routes, and inventory levels. The primary objective of these models is to minimize the total cost, which includes fixed facility costs, transportation costs, and inventory holding costs, all while satisfying demand and capacity constraints. For instance, consider a multinational retail company aiming to optimize its distribution network across North America. The company needs to decide the number and location of warehouses to minimize total costs while ensuring timely delivery to all retail outlets. The MILP model might include variables such as the binary decision to open or close a warehouse, the quantity of goods to be shipped from each warehouse to retail outlets, and the inventory levels at each warehouse. Constraints would include warehouse capacity limits, demand requirements at each retail outlet, and transportation capacity [5]. The model might reveal that by closing two underperforming warehouses and opening one new, strategically located distribution center, the company can reduce overall costs by 12%. Additionally, by optimizing transportation routes, the model could identify a potential 8% reduction in transportation costs, achieving a balance between fixed facility costs and variable transportation expenses. This level of detailed analysis and optimization highlights the power of MILP in designing efficient, cost-effective supply chain networks.

3.2. Production Planning

Production planning is a critical aspect of supply chain management that involves determining the optimal production schedules and quantities for each product at each facility. MILP models for production planning incorporate a range of constraints, including production capacities, setup times, and inventory levels, to develop a comprehensive production schedule. The primary goal is to minimize production and inventory costs while ensuring that customer demand is met promptly. For example, a global electronics manufacturer might use an MILP model to optimize its production planning across multiple factories worldwide. The decision variables in this model could include the number of units of each product to be produced at each factory, the timing of production runs, and the levels of inventory to be maintained at each location. Constraints would involve the production capacity of each factory, the setup times required for switching production lines between different products, and the inventory holding capacities. By implementing the MILP model, the manufacturer could identify an optimal production schedule that reduces total production costs by 15% and inventory holding costs by 20% [6]. The model might suggest producing certain high-demand products in factories closer to key markets to reduce lead times, while producing lower-demand products in factories with lower production costs. This optimization would result in improved customer satisfaction due to shorter delivery times and lower operational costs, demonstrating the value of MILP in production planning.

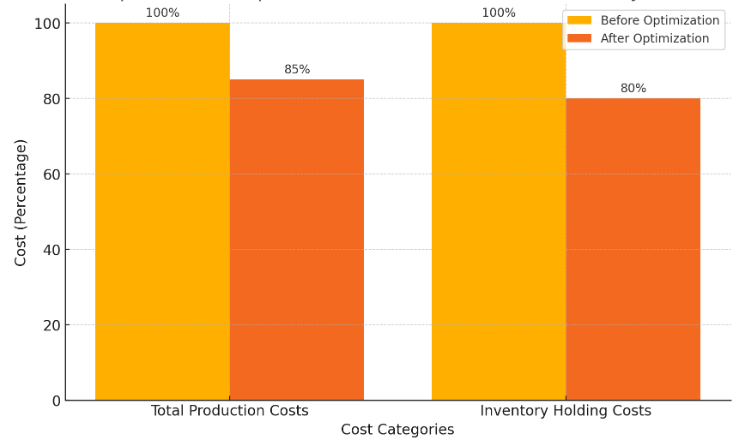
Figure 1. Impact of MILP Optimization on Production and Inventory Costs

3.3. Transportation and Logistics

Transportation and logistics optimization focuses on determining the most cost-effective transportation routes and modes for delivering products from suppliers to customers. MILP models in this area include decision variables that represent transportation modes, routes, and shipment quantities. The primary objective is to minimize transportation costs while ensuring timely delivery and maintaining high service levels. Consider a large e-commerce company that needs to optimize its logistics network to handle increasing order volumes efficiently. The MILP model for this scenario might include variables for selecting transportation modes (e.g., air, sea, or land), choosing specific routes for each shipment, and determining the quantities of goods to be shipped along each route. Constraints would include vehicle capacities, delivery windows, and regulatory restrictions [7]. By using an MILP model, the e-commerce company could identify optimal transportation routes that reduce overall logistics costs by 18%. For instance, the model might recommend shifting a portion of air shipments to sea freight for certain routes where delivery time is less critical, resulting in significant cost savings. Additionally, the model could optimize delivery schedules to ensure that trucks and delivery vans are utilized to their full capacity, reducing the number of trips required and further cutting costs. This detailed optimization enables the company to maintain high service levels while minimizing transportation expenses, illustrating the effectiveness of MILP in transportation and logistics management.

4. Case Studies in Supply Chain Optimization

4.1. Retail Supply Chain

A major retail chain, which operates over 500 stores across multiple regions, faced challenges in managing its extensive supply chain network. The company decided to utilize Mixed Integer Linear Programming (MILP) to optimize its supply chain, focusing specifically on the locations of its warehouses and the management of its inventory. The MILP model considered various factors such as supplier locations, existing warehouse capacities, transportation costs, and demand at each retail outlet. By modeling the entire network, including the potential for new warehouse locations, the company identified that relocating certain warehouses closer to high-demand areas would significantly reduce transportation costs. The optimization process led to the strategic opening of three new warehouses and the closure of two underperforming ones. This reconfiguration resulted in a 15% reduction in overall supply chain costs, amounting to annual savings of approximately $30 million. The MILP model also provided detailed insights into optimal inventory levels at each warehouse. By aligning inventory management with demand forecasts, the company reduced stockouts by 20%, which in turn improved service levels and customer satisfaction [8]. Additionally, the optimization led to a 10% reduction in transportation costs, equivalent to saving $10 million annually. These improvements highlighted the model's effectiveness in balancing cost and service level trade-offs, ultimately enhancing the efficiency and performance of the supply chain network.

4.2. Manufacturing Supply Chain

A global manufacturing firm specializing in automotive components applied MILP to optimize its complex production and distribution network. The firm's network included multiple production plants, distribution centers, and a vast customer base spread across different continents. The MILP model incorporated decision variables such as plant locations, production schedules, and distribution routes, alongside constraints like production capacities, lead times, and transportation costs. The model revealed that consolidating certain production activities and adjusting the production schedules could significantly enhance efficiency. Specifically, the firm decided to centralize the production of high-demand components in plants with the highest capacity utilization rates, which led to a 20% reduction in production costs, saving approximately $50 million annually. Additionally, the model suggested optimizing distribution routes to minimize lead times and transportation expenses. By implementing these strategies, the firm reduced lead times by 25%, improving the average delivery time from 10 days to 7.5 days. This enhancement in lead times was particularly crucial for maintaining competitive advantage in the fast-paced automotive industry [9].

4.3. Pharmaceutical Supply Chain

A pharmaceutical company that produces and distributes a wide range of medications faced the challenge of optimizing its supply chain network to meet stringent regulatory requirements and maintain high service levels. The company turned to MILP to optimize its drug production and distribution processes, focusing on production quantities, facility locations, and transportation routes. The MILP model incorporated variables such as production capacities at different facilities, demand forecasts for various medications, transportation costs, and regulatory compliance requirements. By analyzing these variables, the model identified optimal production schedules and facility locations that minimized costs while ensuring timely delivery of medications. The optimization led to a 20% reduction in production costs, saving the company approximately $25 million annually. This was achieved by consolidating production at facilities with higher efficiency and lower operational costs. Additionally, the model helped streamline the distribution network, reducing delivery times by 15%. The average delivery time was reduced from 5 days to 4.25 days, which was critical for ensuring that life-saving medications reached patients promptly [10].

5. Conclusion

Mixed Integer Linear Programming (MILP) stands as a robust optimization tool, enabling businesses to address the complexities of modern supply chain management effectively. Through its ability to handle integer variables and complex constraints, MILP provides detailed and actionable insights for optimizing production planning, network design, and transportation logistics. The case studies presented in this paper demonstrate substantial cost savings and operational improvements across various sectors. Retail chains achieved significant reductions in supply chain costs and improved service levels through strategic warehouse relocations. Manufacturing firms benefited from streamlined production and distribution processes, enhancing efficiency and reducing lead times. Pharmaceutical companies ensured regulatory compliance while maintaining high service standards and minimizing operational costs. These examples underscore the practical value of MILP in achieving optimized, cost-effective, and efficient supply chain networks. As businesses continue to navigate the challenges of global markets, MILP offers a powerful framework for making informed, strategic decisions that drive performance and competitiveness.