1. Introduction

The Fourier Transform is a crucial mathematical instrument widely used in disciplines such as engineering, physics, and computer science. It is a linear transform technique that aims to transform a continuous or discrete function from its temporal or spatial domain into the spectral domain, which often provides better insight into the characteristics of the analyzed signal [1]. In practical applications, especially in processing of signals, the discrete Fourier transform (DFT) is often used. The DFT is characterized as a finite series of uniformly spaced functions; it is transformed into a series of uniformly spaced parts of the same length as the discrete-time Fourier Transform, which is a function of complex values [2]. Despite the usefulness of DFT, being computationally intensive for large datasets, the need has been felt for a more efficient computation methodology, and thus, the Fast Fourier Transform (FFT) was introduced. FFT means an algorithm that efficiently computes the DFT and its inverse. It hugely reduces the computational complexity, and thus, it becomes feasible to apply Fourier analysis to large datasets.

The most popular FFT algorithm is that of Cooley and Tukey, proposed in the year 1965 by James Cooley and John Tukey. The fundamental concept of this algorithm is the strategy of divide-and-conquer, recurrently breaking down a DFT of size N into smaller DFTs by using the periodicity and symmetry properties of complex exponentials [3]. Thus, it is highly useful in significantly enhancing computational efficiency and accuracy across a broad range of applications, including digital signal processing, image analysis, and more. Although the principles behind DFT and FFT really revolutionized the way data is process and interpret, the growth of datasets into bigger sizes has driven the development of the Sparse FFT (sFFT). The sparsity of the signals is used by the sFFT algorithm to filter and subsample the signal using iterative estimation. It finds the significant frequencies, rather than computing the FFT directly, and zeroing in on them reduces the complexity—a factor that makes sFFT particularly valuable for applications involving large sparse data sets like network traffic analysis, astrophysical data analysis, or large-scale scientific simulations.

The development of the sFFT has undergone various techniques to ensure high accuracy and efficiency. It broadly insulates significant frequencies through random sampling and filtering techniques followed by iterative refinement, correcting minor errors [4]. This allows it to achieve accuracies similar to FFT but with fewer computations. Another significant advantage of sFFT is its inherent noise tolerance. While the FFT takes into consideration the whole dataset in its processing, inclusive of noise, the sFFT is only on the strong frequency components, hence reducing the impact of noise. This kind of selective processing makes sFFT quite suitable for applications like compressed sensing and medical imaging, where clarity of signals is critical [5]. The FFT is a vital is for converting signals from time to frequency, where key characteristics of the signal are revealed. It may not be so obvious from the signal itself. The capability of efficiently calculating the DFT in the form of the FFT has reduced the computational complexity of signal processing. This, however, changed with the discovery of large and sparse datasets, though the Sparse FFT came to exist, which would seek more diminution in computational demands by using sparsity features in signals without sacrificing its accuracy.

This paper aims to provide an in-depth understanding of the Fourier transform, DFT, FFT, and sFFT. Section 2 will present the theory and methods of Fourier transform, DFT, and FFT. Section 3 will examine the development and importance of sFFT, and its benefits compared to the traditional FFT.

2. Methods and Theory

2.1. Fourier Transformation and beyonds

The Fourier Transform breaks down a function into its individual frequencies. It is defined for a continuous signal \( x(t) \) as follows:

\( F\lbrace x(t)\rbrace =\int _{-∞}^{∞}x(t){e^{-i2πf t}}dt,\ \ \ (1) \)

where \( F\lbrace x(t)\rbrace \) is the Fourier Transform of \( x(t) \) , \( f \) denotes frequency, and \( j \) is the imaginary unit. The transform allows for analyses of the function and its frequency to grasp the critical characteristics of the function’s behavior that are hidden or unclear in the time domain [1].

The DFT is defined as a finite series of uniformly spaced parts of a function, which is then transformed into an equal-length series of uniformly spaced parts of the discrete-time Fourier transform, a complex-valued function. The DFT of a discrete function \( f[n] \) with \( 0≤n≤N-1 \) is

\( F[k]=DFT\lbrace f[n]\rbrace =\frac{1}{N}\sum _{n=0}^{N-1}W_{N}^{-kn}, 0≤k≤N-1\ \ \ (2) \)

where \( W_{N}^{-kn} \) is the \( N \) distinct \( {N^{th}} \) roots of unity with \( W_{N}^{-kn}=exp(i\frac{2πk}{N}) \) for \( 0≤k \lt N \) . The DFT transforms a time domain signal into its frequency components, offering a discrete equivalent to the continuous Fourier Transform. Despite its usefulness, the DFT requires \( O({n^{2}}) \) computations, making it computationally expensive for large \( N \) [2].

The FFT is a procedure created to efficiently calculate the DFT and its inverse. The most used FFT algorithm is the Cooley-Tukey algorithm. Developed by James Cooley and John Tukey in 1965, this algorithm utilizes a divide-and-conquer approach, recursively decomposing a DFT of size \( n \) into smaller DFTs, thus taking advantage of the periodicity and symmetry properties of complex exponentials.

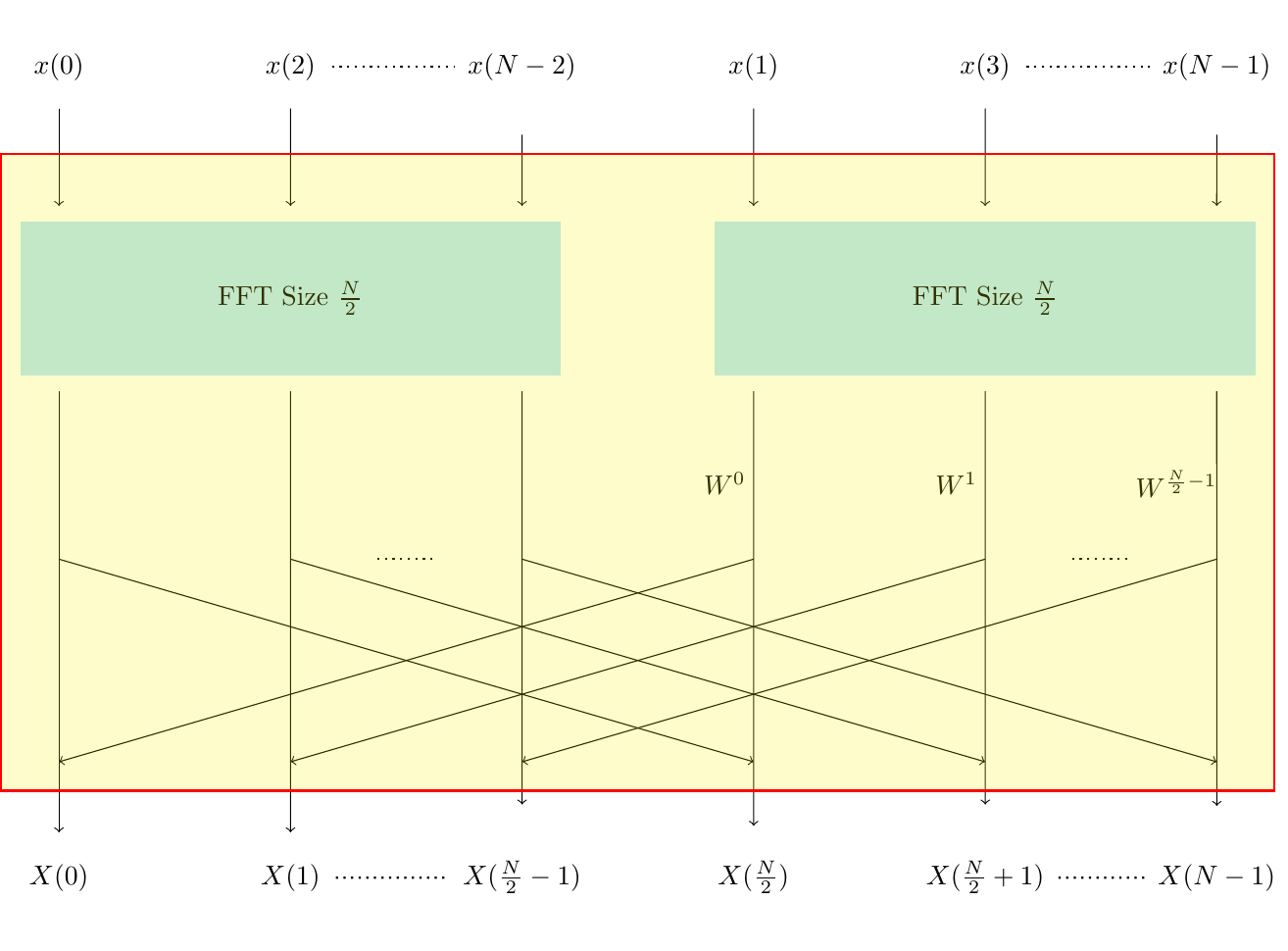
Figure 1. Butterfly Diagram for DFT

This approach, illustrated through figure 1, significantly enhances computational efficiency and accuracy, making it integral to numerous applications in digital signal processing, image analysis, and beyond. Historical developments, including Gauss's early insights and subsequent refinements, underscore the algorithm's enduring impact on both theoretical and applied mathematics.

Executing this method recursively enables the decomposition of a DFT of any decomposed size \( N={N_{1}}{N_{2}} \) ​ into numerous DFTs with reduced sizes.

\( F[k]=\sum _{m=0}^{{N_{1}}-1}{e^{-i\frac{2π}{N}km}}\sum _{n=0}^{{N_{2}}-1}x(m+{N_{1}}n){e^{-i\frac{2π}{{N_{2}}}kn}}\ \ \ (3) \)

Here, complexity goes down from \( O({n^{2}}) \) to \( O(n log n) \) , a huge improvement rendering the practical applicability of Fourier analysis within many applications [3]. This divide-and-conquer approach is the basis of most modern digital signal processing. It allows analysis of large datasets in telecommunications, audio signal processing, and image compression.

The efficiency and accuracy of the FFT have become a cornerstone in many applications. Specifically, the first large area of major application of FFTs is digital signal processing. This includes the analysis of frequency components of signals and their manipulation for telecommunications, audio signal processing, and eventually image compression. Other areas in which the FFT assumes a very important role include scientific computing and engineering applications, where partial differential equations, spectral analysis, and simulations of physical systems are involved.

2.2. Sparse Fast Fourier Transformation

The sFFT is designed to deal efficiently with the sparse signals by concentrating on only their heavy spectral components. Main steps of the sFFT algorithm are: Express input signal in a form that allows sampling in a time domain. Random sampling techniques allow for filtering out noise and data irrelevant for the analysis, hence reducing the size of data and a computational load. Iterative estimation gives the algorithm the necessary refinement in the estimate of important frequency components through successive iterations, by correcting small errors. Identification of the sparse frequency—those of a nonsingular value—is processed, and computational efforts are sure to attach only to data that holds meaning. Finally, all the important frequencies are summed up with their appropriate amplitudes to reconstruct the final frequency domain representation [4].

The inherent noise tolerance is one of the major advantages of the sFFT. Traditional FFT processes a noised full dataset, which can mask the real features of the signal. Unlike the conventional algorithms processing all frequency components equally, it is the focus of the sFFT on strong ones that enables filtering out of noise, turning up a much clearer and more accurate frequency spectrum. This makes the sFFT particularly very useful for applications where clarity of signals holds prime importance, such as in compressed sensing or medical imaging. For example, in medical imaging, denoising using sFFT guarantees that the key features of the images are not lost, which is very important for diagnosis [6].

Given the efficiency and robustness of sFFT against noise, these methods are applied to a wide range of solutions dealing with huge and sparse data sets. In network traffic analysis, the data is usually sparse and contains significant frequencies that refer to some key anomaly patterns. The sFFT as such will help in the effective identification of such patterns; thus, allowing network monitoring and security [7]. Similarly, in astrophysical data analysis where data sets are huge and sparse, sFFT helps in accurately identifying the main celestial phenomena, hence facilitating some important discoveries in the field [8].

Another area was large-scale scientific simulation, which dramatically benefits from sFFT. Such simulations produce vast amounts of sparse data, and the reduced computational complexity of the sFFT enables researchers to process this efficiently to unlock meaningful information. Also, in compressed sensing, where ultimately accurate signal reconstruction uses fewer samples than conventionally required, the ability of the sFFT to find the key frequencies rapidly and with a high degree of precision is highly useful, improving the speed and quality of reconstruction of signals [9].

In conclusion, the sFFT clearly has an edge over the traditional FFT due to its improved noise tolerance and efficiency while handling large, sparse data sets. This ranges from network traffic analysts to astrophysical data analysis, industrial scientific simulations, compressed sensing, and medical imaging. By focusing on significant frequencies and cutting down on computational complexity, the sFFT holds the inherent capability to bring enhanced clarity and accuracy to signal processing, hence making this tool very powerful in meeting modern challenges in data analysis.

2.3. Comparison between FFT and sFFT

Traditional approaches, such as the Cooley-Tukey algorithm, significantly decrease the runtime of the FFT from \( O({n^{2}}) \) to \( O(n log n) \) , thereby enabling numerous real-world applications [10]. Nevertheless, as datasets continue to grow, even this reduced complexity can become limiting.

On the contrary, sFFT is gaining from a decrease in computational complexity because of the sparsity of the signal. It begins working just with the relevant frequency components, and thus it happens to be manifold times quicker for sparse signals. The algorithm brings potential computational complexity down to \( O(n log n) \) , where \( k \) depends on the number of nonzero frequency components. This reduction in computational time and resources makes the sFFT highly efficient for big, sparse datasets [11].

Another important difference between FFT and sFFT is the noise tolerance. This means that with FFT, the entire dataset, including noise, is processed, significantly affecting the accuracy of the estimated frequency components. In contrast, sFFT mitigates the impact of noise by concentrating on the dominant components in the frequency domain. This selective processing inherently enhances the accuracy in the frequency spectrum, so that sFFT finds applications in compressed sensing and medical imaging where clarity of signal is essential [12].

In terms of application, the FFT forms the core of digital signal processing, image analysis, telecommunication, audio signal processing, and scientific computing, where the complete frequency spectrum may have a need. In contrast, the sFFT is helpful in large sparse datasets; typical applications include network traffic analysis, astrophysical data analysis, or big simulations where only some few significant frequencies must be detected and processed [12].

By highlighting these differences, while the FFT is a versatile and powerful tool, the sFFT provides essential improvements in computational efficiency and noise tolerance, making it highly suitable for modern applications dealing with large, sparse datasets.

3. Results and Application

3.1. Applications of sFFT

The sFFT has changed whole areas of science and engineering by giving a better way of processing signals. Medical imaging occupies a special place on the list of the many applications of the theory, specifically in Magnetic Resonance Imaging (MRI). Traditional MRI scans generate vast amounts of data; sometimes, processing takes a while. However, using sFFT significantly reduces the volume of data required with no compromise on image quality, making the scan time shorter and facilitating real-time imaging. The enhancement in patient throughput is not the only application it has added; this new technology makes it easier during surgical procedures where real-time monitoring is in demand [13].

In communication, sFFT finds crucial applications in a wide range of fields, from radar and sonar to cognitive radio networks. These systems work by quickly identifying essential frequencies from large datasets. For example, in radar systems, sFFT allows for real-time object detection and tracking through the fast processing of the reflected signals. In cognitive radio networks, sFFT efficiently identifies available frequency bands that can be used for communications and thus optimizes spectrum usage, minimizing interference [14].

Audio and video compression also enormously rely on sFFT. Traditional compression algorithms use the FFT to project the signals onto the frequency domain. However, most of these signals are known to have many coefficients close to zero. So, by keeping only the significant coefficients, sFFT can provide a better compression rate without a significant loss in quality. This is very important in streaming services because, accordingly, compressed data means a lesser volume of bandwidth and hence increases user experience [15].

For Large Volumes of Information Processing, the processing power of sFFT, according to big data analytics, making it very useful for large volumes of data. In genomics, massive data sets are analyzed to find genetic variations; sFFT will come in handy in speeding up such data processing. Financial market analysis is where, with the fast-processing capabilities of sFFT, it becomes beneficial in real-time analysis of market trends so that traders or analysts can make timely decisions based on updated information [16]. Another area of the emerging application of sFFT is the Internet of Things devices (IoT). Typically, such devices operate with limited power resources and, therefore, need efficient techniques for the processing of data. Lower computational overhead and faster times taken in processing make the sFFT quite suitable for use in IoT's embedded systems, such as wearable health monitors, which work primarily in analyzing physiological data for insights on health in real-time without causing excessive battery drain [17].

3.2. Runtime Comparison on FFT and sFFT

Due to the introduction of sparsity, an intrinsic strength of sFFT over traditional FFT lies in its computational efficiency when caring for sparse signals. Traditional FFT demands a computational runtime of \( O(n log n) \) , which, while efficient for moderate-sized data, becomes impractical as data size grows. Conversely, certain sFFT algorithms exhibit a lower runtime of \( O(k log n) \) , where \( k \) represents the quantity of significant frequencies, thereby greatly reducing computational time and resource consumption [12].

Empirical studies and runtime comparisons have shown the superiority of sFFT in handling large, sparse datasets. For example, simulations in signals with high sparsity have played out where sFFT can be up to 100 times faster than traditional FFT. One graphical representation of this improved performance is depicted in Figure 2, which draws a comparison of the runtime between FFT and sFFT with different dataset sizes. It is shown that the difference between runtime of FFT and sFFT increases upon increasing the size of the dataset, proving that sFFT is scalable and much more efficient in processing large data sets in comparison to FFT.

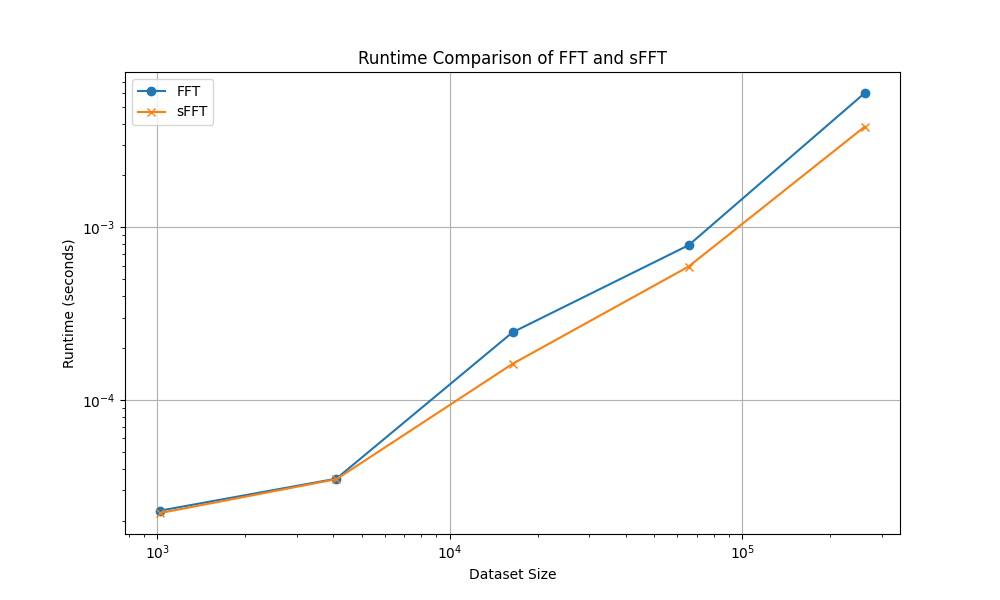
Figure 2. Runtime Comparison between FFT and sFFT

These additional efficiency gains from sFFT will provide significant benefits in applications require low latency. In online gaming or real-time video streaming, where latency should be avoided, sFFT helps speed up the processing of data to provide smoother and more responsive user experiences. On the other hand, the rapid processing abilities of the sFFT version permit real-time analysis of market data in high-frequency trading, where split-second decisions can result in large gains or losses, thus giving traders an edge over their competitors [18].

The reduced computational overhead of sFFT translates to lower power consumption, thus making it ideal for use in embedded systems, IoT devices, and more. For example, the implementation of sFFT provides continuous immediate analysis of physiological data obtained from portable health monitoring devices without excessively reducing the battery life while giving instant health insights to the user. This factor is critical to adopting IoT technology in healthcare, where long battery life and efficient data processing are paramount [19].

It is invaluable in processing gigantic experimental data in scientific research. For example, radio astronomy requires collecting enormous signal data from which meaningful information can be filtered out efficiently using sFFT to eliminate noise and enable astronomers to detect celestial phenomena more quickly and accurately [20]. In particle physics, reading collision data from particle accelerators, for example, sFFT methods are at work in discovering new particles and understanding the fundamental forces. The sFFT has vast advantages over the traditional FFT in terms of computational efficiency and applicability to large, sparse datasets. Such a variety of applications in very different areas guarantees its significant role in modern signal processing and data analysis, turning it into a critical tool for each researcher or industrial professional.

4. Conclusion

The transition from FFT to sFFT introduces new possibilities in the realm of signal processing. The Cooley-Tukey algorithm implemented a divide-and-conquer strategy, significantly enhancing the FFT's utility by treating a DFT as a collection of smaller DFTs. This method dramatically improved computational efficiency, reducing it from \( O({n^{2}}) \) down to \( O(n log n) \) , and thereby making Fourier analysis feasible for a broad spectrum of new applications, including signal analysis, image analysis, and telecommunications. However, as data sizes continue growing exponentially, even FFT's increased efficiency has not been good enough. This requirement for further improvement motivated the development of the sFFT, a technique that uses sparsity in signals to further bring down computational costs. The sFFT explores the sparsity of the signal through examination of only significant frequencies and returns computational complexities in the order of very similarly \( O(k log n) \) , where k is the cardinality of the non-zero frequency components. This makes the sFFT special in domains of applicability to large, sparse datasets, with relevant applications in network traffic analysis, astrophysical data analysis, large-scale scientific simulations, and medical imaging.

However, the sFFT can still be used in applications that pertain to high signal clarity since it inherently allows noisy data to be removed by eliminating excess data. Specifically, this becomes applicable in compressed sensing and medical imaging since it regards reconstruction with high accuracy. The empirical runtime comparison highlights that the sFFT can be up to 100 times faster than the traditional FFT in very sparse signals, underlining scalability and efficiency. This makes the sFFT fit accurately for modern applications like IoT devices and wearable health monitors, where real-time analysis is required along with low power consumption. More importantly, its fast processing helps in cases of high-frequency trading and live streaming where latency is a critical issue. Therefore, the utility of the Fourier transform, extended by sFFT to big data and sparse data sets, makes the technique a robust one against contemporary signal processing challenges. With the growth of data in volume and complexity, the sFFT is fast emerging as a textbook critical innovation that assures an efficient and accurate analysis across a wide range of scientific and industrial applications.