1. Introduction

In the early 20th century 1951, a piece called “Music of Changes” was published, and it was written by John Cage. This work demonstrates John Cage's quest for randomness in his music, to remove the influence of personal intentionality from his work, and to pursue the music itself. He used the I Ching to generate a randomized chart of the different parameters of the music to create this piece. The music in it is determined by the random date that appears in the I Ching rather than by the composer's intentions. In 1952, He presented the famous piece “4’33”, which contains nothing but natural sound effects around the audience. Here the randomness in his music is taken to another level. John Cage is well known throughout the world along with its great controversy. Where exactly are the boundaries of musical randomness? In recent years, randomness in music has risen in tandem with the growing modern quest for innovation in music style. Completely randomness does not exist, yet when it comes infinitely close to what the world calls random, can it still be called music? This article will not delve into the huge philosophical contradictions behind it, but an explore of STFT in the use of generate the randomness in stochastic music. Another influential composer in explored indeterminacy in music is called Iannis Xenakis. His piece "Pithoprakta" applies probability theory and mathematical models.

The STFT appears with the needs of analysis for the non-stationary signals—signals whose frequency content changes over time. In 1946 Dennis Gabor, a physicist and Nobel laureate, brings the idea of analyzing both time and frequency domains simultaneously by use of Gaussian functions as window functions in the traditional Fourier Transform (FT). The alternatives are needed for relaxed translation invariance assumptions [1]. Based on this idea, the STFT is then formalized and perfected in subsequent decades. In the audio analysis field, the STFT usually fits better than the FT or Discrete Fourier Transform (DFT). Compared to FT and DFT, the STFT enables the capture of how frequencies evolve over the timeline. It divides the signal into small overlapping time segments and then applies the Fourier Transform to each segment. The invention of STFT allows further analysis of complex sounds and textures. Jason Brown, a mathematician from Canada successfully replicates the chord in ‘A Hard Day’s Nigh’ by the Beatles using the FT [2]. By transforming and recombining spectral components, STFT allows for the generation of real-time random soundscapes. These technical play an important role in the development of modern random music. The paper will dive deep into the idea of the relationship between STFT and stochastic music.

2. Methods and theory

2.1. The principle of audio digitization

When an audio file is open, it is typically displayed as a waveform in Figure 1. This waveform is not a perfect storage of the original continuous sound signal. If zoomed in, the image will appear as a stepped line as shown, rather than a smooth curve. This discrepancy arises because digital sampling cannot record continuous sound signals. Instead, it records signals by sampling points through a fixed period. This process converts a continuous-time signal into a discrete-time signal.

Figure 1. Top: An audio recording of the author’s voice in Logic. Bottom: Zoom-in graph.

According to The Nyquist Theorem, to accurately reconstruct a continuous-time signal from its samples, the sampling rate must be at least twice the highest frequency component present in the signal.

The Nyquist-Shannon Sampling Theorem so called the Nyquist Theorem has a vital status in the field of signal processing. As shown in Figure 2, the redline is \( y=sin4x \) . If considered as audio signal input, it has the frequency \( 2/π \) . The Nyquist Theorem states the lowest sampling rate to sample this signal and ensure that the original frequency can be restored from the sampled data is \( 2(2/π)=4/π \) . According to this sampling rate, the black spots shown in Figure 2 can restore the original frequency \( 2/π \) . If the sampling rate is less than \( 4/π \) , which violates The Nyquist Theorem, alias will appear when decomposing the signal. As shown in Figure 2 the red spots, can reconstruct more than one possible frequency based on the sampling data. So, to recover all the frequencies in the original signal, the sampling rate must be twice the maximum frequency. This relationship is expressed as:

\( {f_{s}}≥2{f_{max}}\ \ \ (1) \)

Where \( {f_{s}} \) ​ is the sampling rate, and \( {f_{max}} \) is the highest frequency component of the signal.

If the filter can attenuate the above half frequency below the analog-to-digital converter, the aliasing will not appear [3]. It is true that in some special cases, through irregular random sampling, the original signal can be accurately restored when the sampling rate is lower than the Nyquist Theorem states. The upper limit of human hearing is approximately 20kHz. To satisfy the Nyquist criterion, common sampling rates are set at 44.1 kHz, which is more than twice the maximum audible frequency. The higher the sampling rate results the more similar the restored signal to the original.

Figure 2. Graph demonstration in Desmos. The redline is \( y=sin4x \) with the set of black spots being the sampling points at the same time interval \( π/4 \) . The red sampling points have time intervals larger than \( π/4 \) , and its set on both redline and blueline.

2.2. Short-Time Fourier Transform (STFT)

As the Fourier Series was built, it allowed the analysis of sound waves produced by strings and columns. Fourier analyses are used to decompose the naturally occurring harmonics [4]. The Fourier Transform, the predecessor of STFT, allows the transformation of the audio signal to the frequency spectrums. STFT overcomes the lack of time information drawback by considering an analysis window that has a specific time-frequency resolution property. In STFT, a window, which is a function being zero-valued outside of some chosen interval, is employed for extracting time information [5]. Each small-time interval STFT produces applied FFT to reveal the frequency-time spectrum switch. With curtain synthesis, these time segments are combined and construct data that contains frequency values as time progresses [6].

To apply the Short-Time Fourier Transform (STFT) to the signal input, the sampling is divided into a separate time each assumed to be periodic. The STFT function is given by:

\( X(t,f)=\int _{-∞}^{∞}x(τ)∙w(τ-t)∙{e^{-j2πfτ}}dτ,\ \ \ (2) \)

where w(τ−t) is the window function centered at time t, used to extract a time window of the original audio for analysis.

2.3. Categories of audio signals

The convertible audio signals can, based on their spectral image after the STFT, be divided into three broadly defined categories. The expected result for a pure sine wave input is a single peak lies on the exact Hz on the spectrum. The Sinusoidal formula is expressed as:

\( y(t)=Asin(2πft+ϕ)\ \ \ (3) \)

where \( A \) represents the amplitude, \( f \) represents the frequency, and t represents the time. \( ϕ \) is phase, the initial angle at \( t = 0 \) . Sounds with harmonic structures usually refer to the musical notes played by all kinds of instruments. It contains a fundamental frequency additional with multiple harmonics at integer multiples of the original Hz. Natural sound effects are a superposition of random sources, and the spectral values presented with the FT are non-periodic. It is highly randomized and may contain noise with no apparent peaks. To obtain randomized input data, the natural sound effects are always chosen due to their complex and varied spectral characteristics.

2.4. Time-frequency trade-off

Time and frequency domains are two mutually exclusive representations of audio signals. The frequency spectrum represents the average of all times, and the time domain represents the average of all frequency values as time goes on [7]. A segment of audio samples is transformed into a spectrum by the STFT as the data is converted from the time domain to the frequency domain. This transformation highlights the Time-Frequency Trade-off. Heisenberg’s Uncertainty Principle states that one cannot simultaneously achieve arbitrary precision in both time and frequency domains. Mathematically, this principle is expressed as:

\( ∆t∙∆f≥\frac{1}{4π}\ \ \ (4) \)

To illustrate the concept of random music generation, this paper will not consider the middle tradeoffs situation and only focuses on analyzing signals either entirely in the time or frequency domain.

3. Results and Application

3.1. Manipulating and reconstruct

A way to introduce randomness in the music generation is to modify the values obtained in the spectrum. This can be done by altering the magnitude and phase components of the STFT output. The original phase contains information on the temporal structure of the original sound. Embedding random algorithms to specific frequency bins can result in the adjustment of amplitude. More chaotic effects can be created if both sound magnitude and phase are randomized.

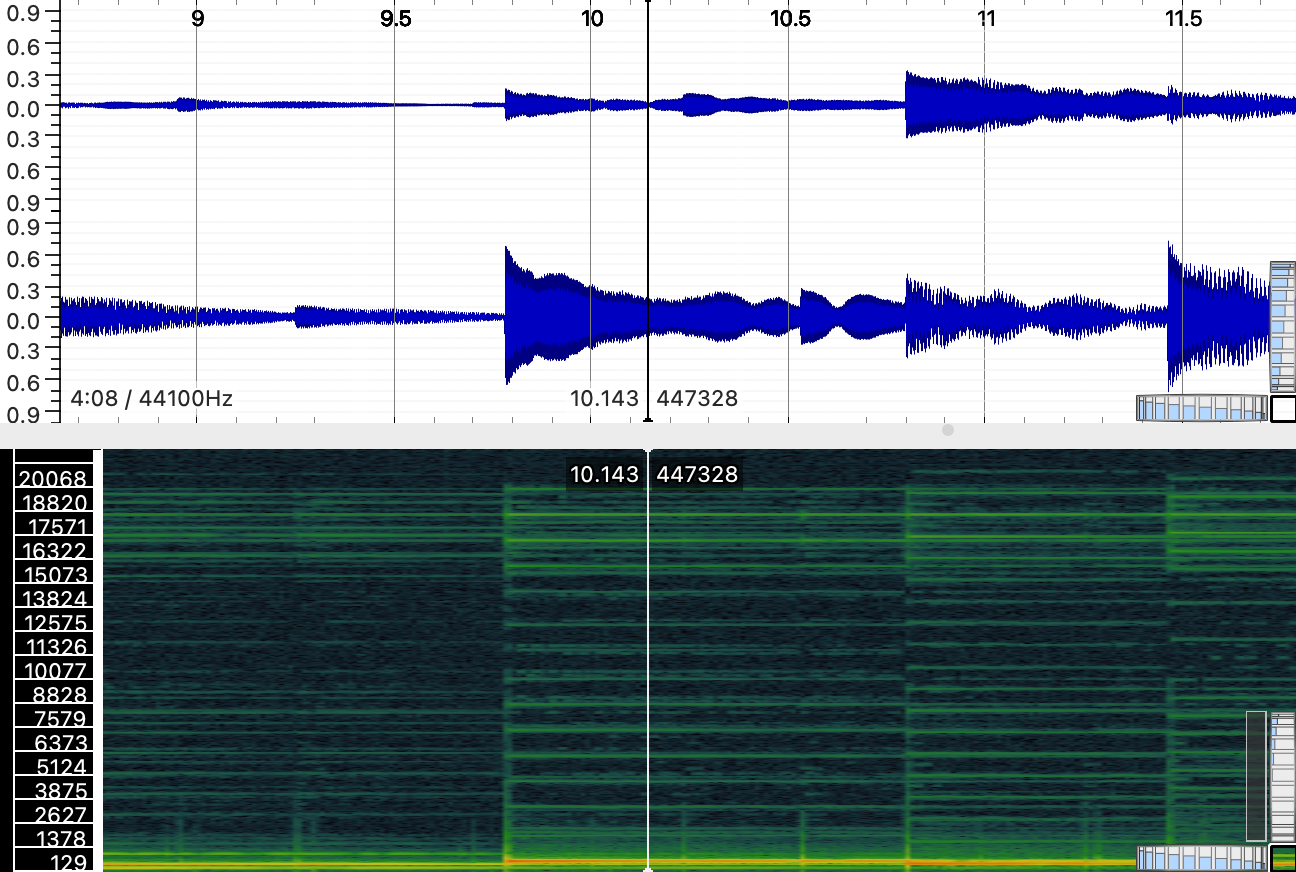
Figure 3. Real-time conversion diagram of a sound source from time domain to frequency domain in Sonic Visualiser.

For example, in Figure 3, modified data of the frequency spectrum values in some will result in fresh audio output. The modified STFT representations are converted back to the time domain using the inverse STFT (ISTFT). The ISTFT reconstructs the time-domain signal by integrating the modified spectra across all frames, windows stitch together seamlessly by overlap and add method. The new audio sounds will retain the temporal dynamics of the original sound but with randomized spectral characteristics.

Randomization of sound spectrum values serves as the foundation for creating random music. By applying different randomization strategies to the spectra and experimenting with various window sizes and overlap ratios, a diverse range of musical textures and effects can be generated. The article "Short Time Fourier Transform Based Music Genre Classification" by Ahmet Elbir, Hamza Osman Ilhan, Gorkem Serbes, and Nizamettin Aydin, presented at the 2017 25th Signal Processing and Communications Applications Conference (SIU), explores the use of Short Time Fourier Transform (STFT) for music genre classification. This paper evaluates the impact of six window types used in the STFT extraction step on music genre classification [8]. Additionally, interactive elements can be incorporated by linking the randomization parameters to external controls, allowing real-time manipulation of the generated music.

3.2. Application in real life

Jean-Claude Risset is a famous computer musician, well known for his innovative works in the field of sound synthesis and spectral analysis. With a simple version Fourier transform technique, he successfully decomposes the audio signal into constituent sine wave components. Risset put a lot of effort into researching the components of sound and how to resynthesize it with the FT techniques. The spectral techniques allowed precise control of analyzing the harmonic sound over the timeline. In 1985, He presented a piece called "Sud". In this piece, he decomposes natural sounds and re-synthesizes them to create a seamless blend of acoustic and electronic textures.

The works of Bell Labs contribute to the whole scientific world including building the foundation for the development of computer music software and techniques. Tenney did research in computer music techniques including FT-related synthesis at Bell Labs in the 1960s. He applied principles related to Fourier analysis to explore the stochastic nature of sound. In 1961, Tenney published a work called "Analog #1: Noise Study", in which he used noise and its spectral properties as the elements of this composition.

The first computer music-generated sound is produced by Max Mathews’ MUSIC software, using the temporal envelope modulates Fourier series to define the timbre of instruments [9]. In Max/MSP STFT is used to analyze and resynthesize grains. This technique allows the dynamic manipulation of the pitch of the sound. And adjusts the timbre and duration of the audio signal. Simplifying the instructions software makes STFT and ISTFT easier to operate for their user. Effects such as spectral gating, morphing, and filtering can be implemented by manipulating the frequency components obtained from STFT. Like Max, Pure Data (Pd) is an open-source visual programming language for audio and multimedia processing. The real-time effects such as time-stretching and pitch-shifting can be made through Pd using STFT during the live performance. The Ableton Live, as many producers are familiar with, exists lives’ warping features to align beats and harmonies from different tracks, creating seamless transitions and remixes. This includes advanced warping and stretching algorithms that rely on STFT for time-domain manipulation. Sound designers use STFT-based tools in Ableton Live to manipulate audio, creating granular textures and complex rhythmic patterns. In Ref [10], the author discusses the technique of classifying the music genres by input time-frequency spectrum to machine learning.

4. Conclusion

The paper introduces in detail the specific process of audio digitization and highlights the critical role that STFT plays in frequency randomization. The time and frequency tradeoff that is generated by STFT is been used widely in music randomization. By dividing the signal into separate time Windows, STFT can analyze the frequency components that change over time, thus it can be applied to the non-stationary audio signal. It provides a powerful tool for the innovation of digital music. The sound generated by the modulation of its frequency spectral is quite random and develops dynamically along the timeline. Achieved randomness and dynamics through the modulation spectrum of STFT have a wide range of application prospects. Not only in the field of music but also in fields such as signal processing, communication encryption, and audio engineering. This paper shows the significant impact of STFT technology on contemporary experimental music, demonstrating its potential to create new sound textures and expand the boundaries of music innovation. Many of the more complex sound syntheses and analyses of modern times are built on STFT. By leveraging the capabilities of STFT, musicians and engineers can explore new avenues for digital sound synthesis, resulting in innovative auditory experiences