1. Introduction

Starting from the first pulsed laser in 1960, laser technology has had a rapid development in the last decades. CPA technology (Chirped pulse amplification) is the key technology driving the development of laser physics. Starting with the inventors Mourou et al. [1], lasers have gradually broken through the initial kilowatt power limitations into today's megawatt, megawatt, and even exawatt power ranges through CPA. Jin is a leader in researching ultra-high lasers. In 2019, the research by applying wavefront correction to a multi-beat-watt (PW) titanium gemstone laser and using an off-axis parabolic mirror for tight focusing, the research team achieved \( 5.5×{10^{22}}W/{cm^{2}} \) of laser intensity [2]. In 2021, his team used a CoReLS beat-watt (PW) laser with a two-stage adaptive optics system with f/1.1 off-axis parabolic mirrors for wavefront correction and tight focusing to achieve \( 1.1±0.2×{10^{23}}W/{cm^{2}} \) peak intensity of the laser by measuring 80 consecutive laser pulses [3].

Ultra-intense laser fields are extremely important in the QED effect. The QED effect may occur in the interaction of an intense laser pulse with a retrograde electron beam [4]. The effect of a normal, low-power laser field on electrons is not strong. In contrast, if the power of the laser field reaches \( 5×{10^{22}}W/{cm^{2}} \) , laser-electron interactions will take place and result in the creation of multiple electron pairs from a single beam of electrons. In QED, such a field is considered strong if the electric field E exceeds the Schwinger limit \( E≥{E_{S}}=e{λ_{C}}{m_{e}}{c^{2}} \) [5]. Such a field has the potential to separate virtual electron-positron pairs and provide energy in excess of the rest mass energy of the electron \( {m_{e}}{c^{2}} \) . An electron's scattering process occurs in a strong laser field absorbs multiple photons and emits a single high-energy photon, which is known as nonlinear Compton scattering. An electron moving at relativistic speeds will radiate a high-energy photon, which is the radiative inversion of the electron, and it will greatly affect the electron energy and trajectory.

Typical QED strong-field effects include the creation of pairs of electrons and positrons from the emission of high-energy photons from the electrons or positrons, high-energy photons, i.e., Compton scattering, and the development of a cascade caused by these two processes. In QED, electron-positron pairs are called Polarized Particles, and they exhibit polarization effects in strong fields, i.e., the electrons and positrons are separated by the field force, resulting in a change in the distribution of charge and magnetic moment in the vacuum. This change affects the nature of light propagation in a vacuum. In QED theory when a strong electromagnetic field (e.g., a strong laser field or a strong magnetic field) is applied to the vacuum, virtual particle pairs (electron-positron pairs) are created, and these virtual particle pairs lead to the polarization of the vacuum, which causes the vacuum to exhibit a birefringence effect similar to that of an anisotropic medium. Using flying focused pump lasers, it is expected that this phenomenon will be directly observed in future experiments [6].

This paper is devoted to summarize the recent advancements in the study of the strong-field QED effect in recent years, especially since 2020, to discuss the basic theoretical framework of QED, and then to focus on the particle generation part, spin, with important applications, to study the applications and results of strong-field QED. Attention is also given to future approaches that may have a significant impact on the study of strong-field QED.

2. Description of electrons in a QED-intense laser field

When the electrical field surpasses the threshold known as the Schwinger limit: \( E≥{E_{s}}={m_{e}}{c^{2}}/e{λ_{c}} \) , it will be considered a strong field. In the focal region of the laser, a QED strong field can be generated. For very strong laser intensities, e.g. \( J≈{10^{22}}W/{cm^{2}} \) or even higher, a retrograde particle will experience a QED field in a one-dimensional wave. Apart from this, the electric field in the laboratory frame of reference is not considered a strong field in the context of QED [4]. This is because a particle \( a(η), η=ωt-(k\cdot x) \) traveling retrograde in a one-dimensional wave rises in frequency in the electron's frame of reference, such that the electron's unitless energy E and momentum are correlated with \( {m_{e}}{c^{2}} \) and \( {m_{e}}c \) . k is the projection in the direction of the wave propagation. QED strong field: \( {E_{0}}=|dA/dη|ω(E-{p_{//}})/c \) If the \( χ={E_{0}}/{E_{s}}≥1 \) , upon Lorentz transformation, the field surpasses the Schwinger limit. After conversion, the value of \( χ \) can be expressed as:

\( χ=\frac{1.5{λ_{c}}}{λ(E-{p_{//}})|\frac{dA}{dη}|}≈\frac{(E-{p_{//}})}{1.4×{10^{3}}}\sqrt[]{\frac{J}{{10^{23}}W/{cm^{2}}}}\ \ \ (1) \)

Here, \( J \) is the local instantaneous intensity of the laser. When increasing the laser field intensity to \( 5×{10^{22}}W/{cm^{2}}(|a|≈110) \) , \( χ≈90 \) . When increasing the laser field intensity to \( 1×{10^{23}}W/{cm^{2}} \) , \( χ \) will be extremely large and the QED effect is extremely significant.

Nonlinear Compton scattering (NLC) and multiphoton Breit-Wheeler (BW) pair generation are two common phenomena in Quantum Electrodynamics (QED). Among them, the multiphoton Breit-Wheeler (BW) process is an important strong-field quantum electrodynamics (QED) phenomenon describing the generation of electron-positron pairs by the annihilation of high-energy photons in a strong electromagnetic field. The classical Brett-Wheeler process entails the interaction of two high-energy photons, resulting in the production of an electron-positron pair. Conversely, in the multiphoton BW process, a single high-energy photon engages with multiple low-energy laser photons to produce the same result. This nonlinear effect requires extremely high laser field intensity and high-energy photons. Experiment E-144, discussed at the SLAC meeting, an important conference for the study of QED, measured these two strong-field QED processes for the first time. the NLC scattering, i.e., photon emission due to electron-laser interactions, takes the process form \( e+​{n_{L}}{γ_{L}}​→{e^{ \prime }}+γ \) . the multiphoton BW process takes the form \( γ+{n_{L}}{γ_{L}}​→{e^{+}}{e^{-}} \) generating electron-positron pairs. In order to exceed the threshold, the participation of \( {n_{L}}=5 \) laser photons were required in the E-144 experiment, which was confirmed experimentally [7]. The sketch of the processes is shown in Fig. 1.

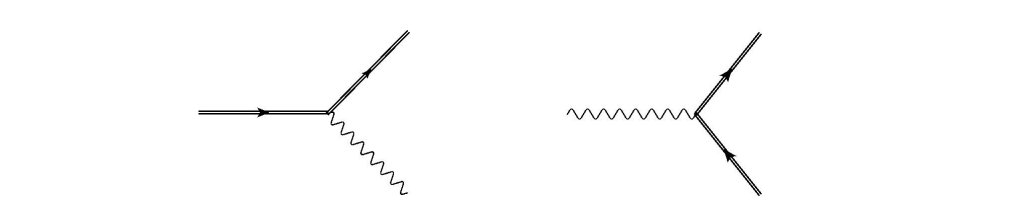
Figure 1. Nonlinear Compton scattering (emission of photons, left panel) and nonlinear Breit–Wheeler pair generation (right panel) [7].

3. Particle generation processes

In the QED effect, an important route for particle generation is the aforementioned nonlinear Compton scattering (NLC) and multiphoton Brett-Wheeler (BW) pair generation. Theoretically, this two-step process can be achieved with just one step via virtual photon exchange. This process is known as the three-step process for Volkov electrons. Fig. 2 illustrates the Feynman diagram of this trident process. Using the saddle-point method, an analytic result for its generation probability can be obtained:

\( f({a_{0}})=4{a_{0}}\lbrace (2+{{a_{0}}^{2}}){sinh^{-1}}{(\frac{1}{{a_{0}}})}-\sqrt[]{1+{{a_{0}}^{2}}}\rbrace \ \ \ (2) \)

In experiment E-144, the probability of the experiment is consistent with the theory.

Using the Weizsäcker-Williams approximation, it is possible to estimate the scattering cross section generated by the direct trident pair. Using an extremely simplified form, the nonlinear inverse Compton scattering differential cross section formula can be written as [8]:

\( \frac{dσ}{dΩ}∼\sum _{n}{|Mn|^{2}}δ({E_{f}}-{E_{i}}+nℏω)\ \ \ (3) \)

Results show that the cross-sectional area generated by direct trident pairs is diminished by a factor of a thousand relative to that of the two-step process (nonlinear Compton scattering followed by BreitWheeler pair generation) [7]. The generation rate R is denoted as:

\( R∼exp(\frac{f({a_{0}},{b_{0}})}{χ})\ \ \ (4) \)

where the function \( f({a_{0}}​) \) is of the form:

\( f(a0)=-\frac{8}{3}(1-\frac{1}{15{{a_{0}}^{2}}}+O({{a_{0}}^{-4}}))\ \ \ (5) \)

The results of the E-144 experiment show that the observed energy spectrum of the scattered photons agrees with the theoretical predictions, thus validating the mechanism of scattering of energetic electrons under intense laser conditions. In recent years, a concept for probing SFQED by utilizing a highly charged, ultra-relativistic electron beam interacting with a solid conductive target has been proposed, which can attain interaction scenarios similar to those anticipated in beam-beam interactions, utilizing only a single-beam apparatus, in order to achieve a method of investigating SFQED under low-laser-intensity or no-laser-field conditions [9]. Tim Adamo et al. studied the strong-field QED processes of electrons and photons in the context of an ultrahigh-energy accelerated particle beam. The authors consider the electromagnetic field of an ultrahigh-energy particle beam as a superposition of random plane waves, and obtain a wave-function representation of fermions by solving the Drake equation in the background in order to compute the amplitudes of scattering in elastic collisions, nonlinear Compton scattering, and nonlinear BW processes. This is done by expressing the amplitudes of these processes as amplitude averaged over a plane wave background [10]. Seen from left panel of Fig. 3, as the overall charge of the beam increases, it is well represented by the shockwave. Regarding to the right panel of Fig. 3, at constant field strengths, the cross sections of the beam and shockwave vary at high momentum transfer q, examining the beam's microstructure [10].

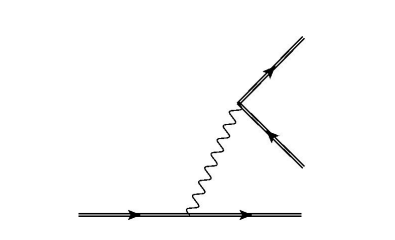
Figure 2. Provides a depiction of the trident mechanism involving Volkov electrons. The phenomena illustrated in Figure 1 can be produced by severing the internal photon line [7].

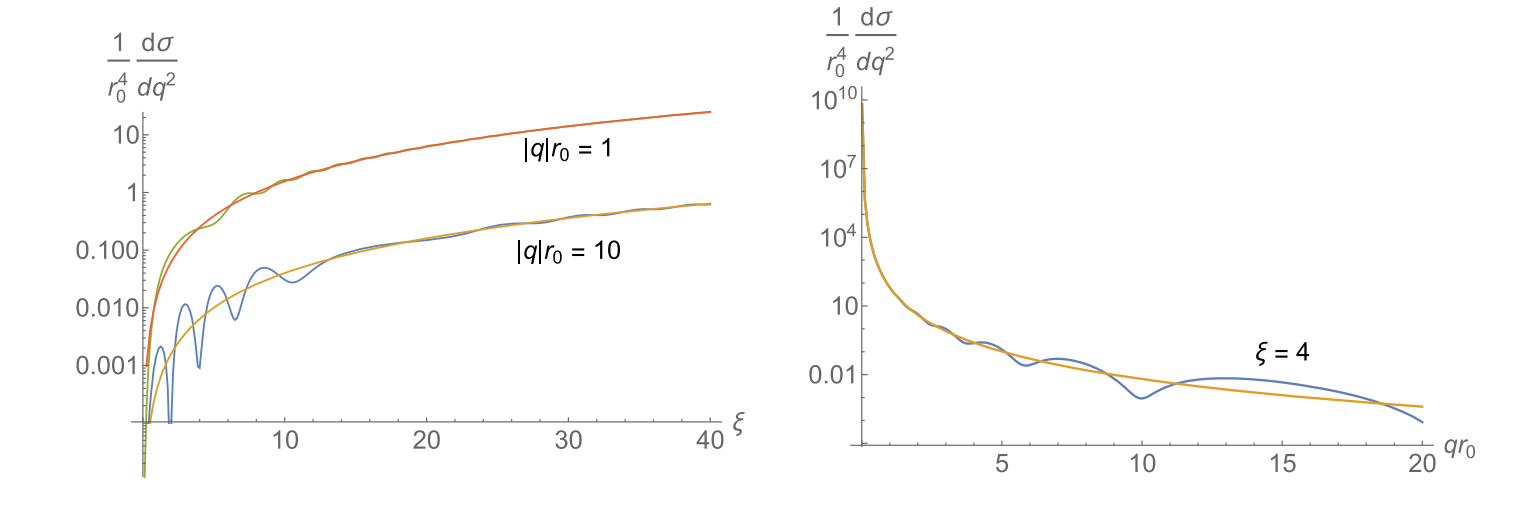
Figure 3. A contrast of the differential cross section (integrated along the z-axis) in the contexts of beam and shockwave [10].

4. Spin-relevant evens

In quantum electrodynamics, spin is of great physical importance. During nonlinear Compton scattering, where an electron absorbs multiple laser photons and then emits a single high-energy photon, the spin state of the electron has a significant effect on the scattering cross section. Previous indicates that in strong-field QED, the radiation probability of an electron in an ultra-intense laser field significantly depends on its spin state [11]. Exact solution in the Volkov electron plane wave background field. In LCFA, it is assumed that the strong field can be considered as a local constant field within the formation length, thus simplifying the calculations. The spin-dependent radiation probability can be expressed as:

\( \frac{dP}{dτ}=-αb\int dt[{Ai_{1}}(z)+\frac{gA{i^{ \prime }}(z)}{z}+Ξζ\frac{sgn(\dot{h})Ai(z)}{\sqrt[]{z}}]\ \ \ (6) \)

where \( Ai(z) \) is the Airy function, \( Ξ \) is the component of the initial electron polarization vector, \( ζ \) is the electron spin direction. In an ultra-intense laser field, the spin state of the electron flips asymmetrically, similar to the Sokolov-Ternov effect in a storage ring. Radiation probabilities for spin-flip and non-flip are given in the literature [11]:

\( \frac{{dP_{nonflip}}}{dτ}=\frac{-α}{2b}\int dt[2{Ai_{1}}(z)+\frac{(g+1)A{i^{ \prime }}(z)}{z}+\frac{ζΞ(2t-{t^{2}})}{1-t}\frac{Ai(z)}{\sqrt[]{z}} \\ +\frac{{Ξ^{2}}κ{t^{2}}}{(1-t)}({Ai_{1}}(z)+\frac{A{i^{ \prime }}(z)}{z})]\ \ \ (7) \)

\( \frac{{dP_{flip}}}{dτ}=-α/2b\int dt[\frac{{t^{2}}}{1-t}\frac{A{i^{ \prime }}(z)}{z}+ζΞ\frac{Ai(z)}{\sqrt[]{z}}-\frac{{Ξ^{2}}κ{t^{2}}}{(1-t)}({Ai_{1}}(z)+\frac{A{i^{ \prime }}(z)}{z})]\ \ \ (8) \)

These equations elucidate the alteration in an electron's spin configuration after photon emission. The parameters Ξ and ζ specifically and capture the influence of the initial polarization and spin orientation of the electron. Nonlinear Compton scattering can quickly induce the spin polarizability of the electron. In addition, the polarization generation of gamma photons is closely related to the polarization of laser photons and the spin state of electrons. Regarding Strongly NLC, when an ultra-intense laser pulse collides with an ultra-relativistic electron beam, the polarization of gamma photons is primarily governed by the electron spin configuration. Given that the trajectory deflection angle of the electron in the laser field is significantly greater than the angle of the radiation cone, the formation length is minimal with respect to the inhomogeneous length of the field. In this case, the spin state of the electron has a significant effect on the polarization of the gamma photon. Based on the derivation, the polarizability of the generated gamma photons can be obtained:

\( {P_{γ}}=\sum _{sf}\frac{({|{M_{si→sf}}|^{2}}-{|{M_{si→-sf}}|^{2}}}{({|{M_{si→sf}}|^{2}}+{|{M_{si→-sf}}|^{2}}})\ \ \ (9) \)

where \( {P_{γ}} \) is the polarizability of the gamma photon and \( {M_{si→sf}} \) denotes the matrix element from the initial state spin \( si \) to the final state spin \( sf \) . A comparison is shown in Fig. 4. Probabilistic formulae for the emission of fully polarization-resolved high-energy photons and for the generation of electron-positron pairs are derived under the quasi-classical approximation and the local constant field approximation (LCFA) employing the quantum operator method of Baier and Katkov [13]. Polarization generation of gamma photons is also investigated as affected by the spin state of the electron. The formulas for the polarizability of the generated gamma photons are the same as in Ref. [11] and the results can be verified to be correct.

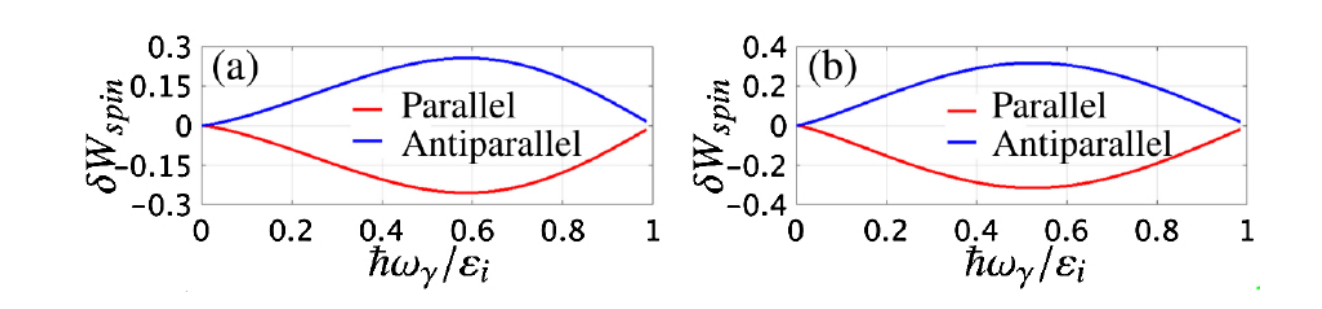
Figure 4. The comparative magnitude of the spin-related component in the probability of radiation for χe = 1 (left) and 0.1 (right). The red/blue curves indicate Si aligned and anti-aligned with SQA, specifically [12].

5. Other proposal applications

5.1. Vacuum Birefringence in QEDs

The vacuum is not empty in the framework of quantum electrodynamics, but is filled with the rise and fall of virtual particles. According to quantum field theory, Under the influence of an applied electromagnetic field, virtual e⁻ e⁺ pairs can cause polarization of the vacuum. leading to a change regarding the transmission characteristics of EM waves in vacuum: the propagation of a photon in the vacuum appears similar to the propagation of light in a birefringent medium, called vacuum birefringence. The vacuum birefringence effect was first proposed by Heisenberg and Euler in 1936, who used a one-loop effective Lagrangian quantity to describe the electrodynamic corrections under strong fields. This correction considers the polarization effect of virtual e⁻e⁺ pairs within the vacuum, which results in vacuum exhibiting nonlinear optical properties [14]. The vacuum birefringence effect in QED has not yet been verified directly by experiments, but numerous experiments such as the PVLAS experiment [15] and others are now available, which provide valuable experience for the development of direct observations and theoretical studies of vacuum birefringence.

5.2. Angular momentum photon effect in QEDs

The angular momentum photon effect is mainly concerned with the fact that by interacting with a plasma using a circularly polarized LG laser, the spin angular momentum (SAM) and orbital angular momentum (OAM) driving the laser can be transferred to electrons, which in turn are transferred to high-energy gamma photons by quantum radiation. This interaction can be illustrated using a 3D quantum electrodynamic particle-in-cell (PIC) simulation that depicts the topological charge, chirality, and CEP of the photon. Moreover, the orbital angular momentum (OAM) of the photons is transferable to the electrons via the interaction, thus affecting the trajectory and radiation properties of the electrons. The forces on the electrons in this laser field have a helical structure, causing the electrons to move along the helical path. During the process, the radiated photons also inherit part of the angular momentum, leading to the spiral characteristics of the radiated photons. This radiation pattern is different from the conventional linear radiation pattern. In a high-intensity laser field, the electrons are able to obtain higher energies, resulting in the production of higher-energy gamma photons. The helical structure of the OAM photons enhances the generation efficiency of such high-energy photons [16].

6. Limitations and prospects

Currently, the research on strong-field QED is developing rapidly, and the theoretical part of QED has been developed in a very powerful way. The description of QED is very precise and is supported by a strong theory, which allows simulations to be performed to get the expected correct results. A variety of effects have been predicted, and current experiments are gradually confirming them. However, the experimental part of the study is not perfect, and with respect to the laser part, current lasers have recently reached the order of \( {10^{23}}W/{cm^{2}} \) , but to detect the more pronounced and relevant cascade processes, and other effects derived from QED, lasers of the order of \( {10^{24}}W/{cm^{2}} \) and even higher may be needed. of order of magnitude. In addition, there are many QED effects that have not been directly observed experimentally, such as vacuum birefringence with more intense cascade processes. However, the problem is now being gradually solved: laser technology is progressing and will reach the order of \( {10^{24}}W/{cm^{2}} \) soon, and, low laser fields versus no laser field and only one ultra-relativistic electron beam are now being gradually explored to study SFQEDs. It has been mentioned in Sec, 3. This research will lead to a breakthrough in the future development of QEDs.

7. Conclusion

To sum up, a more comprehensive discussion of strong-field QED based on ultra-intense lasers is presented in this study. With a laser of sufficient power, the field exceeds the Schwinger limit and the particle will exhibit QED effects. The laser interacts with matter, generating positive and negative electron pairs and gamma photons with a series of cascade effects, using the QED parameter χ to measure the strong-field QED effect and a discussion of its basic definition. The role of spin in QED is investigated, with implications for scattering cross sections and models, and applications such as vacuum birefringence and the angular momentum photon effect, which are important in QED, are discussed. the limitations of current strong-field QED are summarized, and more methods for implementing QED are discussed. this paper summarizes QED research since the 20th century, and highlights new developments since 2020, in anticipation of a more robust future for QED. The paper summarizes the QED research since the 20^th century and focuses on the new developments since 2020 in the hope that more excellent methods will emerge in the future.