1. Introduction

The price of housing has always been a hot topic in every country. Accurate forecasting of house prices is a key undertaking in the real estate market and has a major impact on buyers, sellers, and policymakers. In addition, identifying which factors affect housing prices is the most popular research topic among the stakeholders. Jiang and Qiu analyzed the price of land acquisition had a significant positive impact on housing prices, and disposable income had a smaller positive effect on housing prices [1]. Dong used the data on housing prices in New York City to conduct an analysis. The result concluded from his study was the appreciation rate of average home prices is mostly influenced by the volume of real estate transactions after the component of real estate location is eliminated [2]. Zhao and Liu analyzed the impact of housing policy using a methodical quantitative literature analysis. [3]. Their research identified three distinct forms of housing policies that have an impact on the real estate market: monetary policies, tax policies, and macro-prudential policies [3].

There are many models and methods that can be used in the process of predicting house prices. Sagala and Cendriawan developed a linear regression model using a dataset from the Maribelajar company to predict housing prices [4]. The data analysis and testing conducted in this research demonstrate that the multiple linear regression model can predict and assess home prices to a specific extent [4]. Nevertheless, the algorithm might be enhanced further by including more sophisticated machine-learning techniques. Wang et al. provided a comprehensive joint self-attention model for predicting property prices [5]. The suggested model has a minimal prediction error and surpasses the performance of the previous models. Moreover, Thamarai and Malarvizhi conducted decision tree regression, decision tree classification, and multiple linear in their paper based on desired attributes and predicted housing prices [6]. Among the many studies on real estate price prediction, most of them concentrate on the forecasting of house prices in large cities. Wang et al. created a flexible spatiotemporal model to investigate the spatiotemporal features of residential prices and the influencing variables in middle-small cities [7]. They applied the model to conclude that government policies have a substantial effect on the cost of housing, causing their characteristics to differ from those of large cities. Park and Bae also created a model for forecasting prices, utilizing machine learning algorithms like C4.5, RIPPER, Naïve Bayesian, and AdaBoost, and compared the performance of their classifying accuracy [8]. The Repeated Incremental Pruning to Produce Error Reduction method consistently beats other models in accurately predicting home prices, as demonstrated by the experiments.

Furthermore, The Gradient Boosting Model XGBoost was used in a study to predict Karachi real estate values. It uses a dataset of 38,961 entries that it collected from an open real estate portal in Pakistan, and it achieves an impressive accuracy of 98% [9]. Research indicates that both the characteristics of the location and the physical structure of a property play significant roles in forecasting its price. Brannlund et al. discovered that support vector regression and multilayer perceptron can outperform a linear model in predicting property values and resales, but statistical significance is not always evident [10]. Future studies should investigate other data sets for comprehensive use.

The purpose of this article is to construct a multiple linear model to analyze which factors have a significant effect on house prices in the U.S. In addition, it compares several commonly used models for predicting house prices and thus concludes which model can most accurately predict house prices.

2. Methodology

2.1. Data source

The data utilized in this study is “Housing Price Prediction,” which can be downloaded from the Kaggle website. It was compiled by Harish Kumar, who sourced the data from various websites and published the entire housing price dataset in 2023. There are 545 observations and 13 variables in the dataset.

2.2. Variable selection

The dataset includes one dependent value (Housing Price) and 12 independent values. Table 1 displays the details for the housing price dataset:

Table 1. List of Variables

2.3. Method introduction

The study adopts a multiple linear regression model to select the influencing factors for housing prices. Multiple Linear Regression (MLR) is a statistical approach for representing the correlation between a single response variable and two or more explanatory variables. It is represented by the following equation:

\( Y={β_{0}}+{β_{1}}{x_{1}}+⋯+{β_{n}}{x_{n}}+ϵ\ \ \ (1) \)

Where \( Y \) is a response variable (housing price in this paper), \( {x_{1}} \) … \( {x_{n}} \) are explanatory variables, \( {β_{0}} \) is an intercept term, \( {β_{1}} \) … \( {β_{n}} \) are the coefficients for each explanatory variable \( {x_{1}} \) , \( {x_{2}} \) … \( {x_{n}} \) . \( ϵ \) is an error term.

The advantage of multiple linear regression models is that they quantify the correlation between the response variable and each factor. They might lead to a clearer understanding of the connection between every individual component and the result [11].

3. Results and discussion

3.1. Data preprocessing

This dataset does not include any empty data. However, it is evident that the dependent variable exhibits a right-skewness, as seen by the Figure 1 presented below:

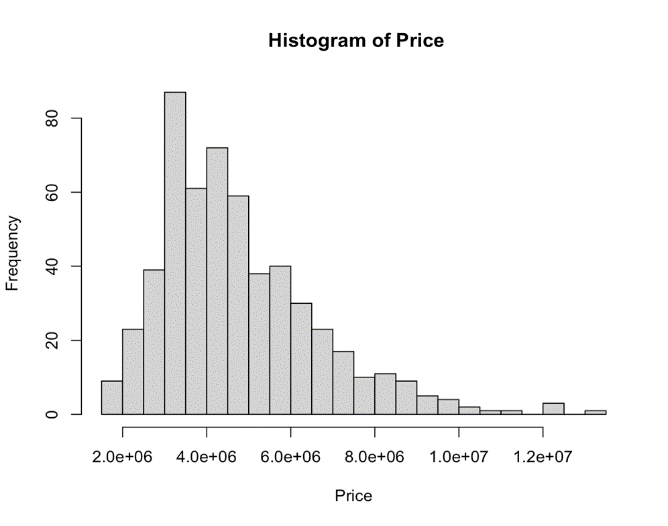
Figure 1. Histogram of Housing Price

Logarithmic transformation is an effective technique for stabilizing variance and reducing skewness, resulting in more dependable and easily understandable outcomes. Utilizing a logarithmic transformation on the dependent variable (Price) mitigates the presence of right-skewness. As the Figure 2 shows:

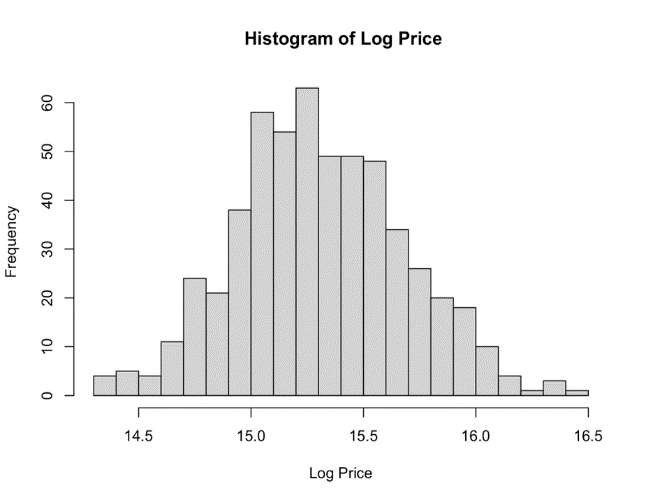
Figure 2. Histogram of Housing Price after Applying Logarithmic Transformation

There is only one remaining outlier after the dependent variable (housing price) is checked in the boxplot below. It is advantageous to eliminate this observation in order to enhance the precision of subsequent experiments. The number of observations is reduced from 545 to 544 by employing the Interquartile Range (IQR) method, which eliminates 0.02% of the original dataset (Figure 3).

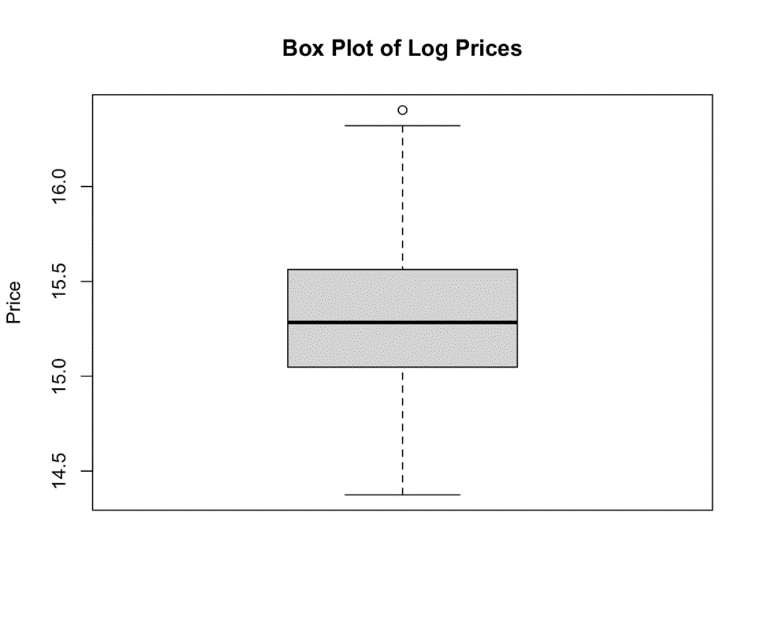
Figure 3. Boxplot of Log Housing Price

3.2. Model results

Using the transformed data set, a multiple linear regression model (MLRM) was fitted to determine the significant factors influencing housing prices. The model below is defined as a full model:

\( Y={β_{0}}+{β_{1}}{x_{1}}+⋯+{β_{12}}{x_{12}}+ϵ\ \ \ (2) \)

Where \( {x_{1}}, {x_{2}},…,{x_{12}} \) correspond to the independent variables in the transformed dataset, \( {β_{0}} \) is a constant term, and \( ϵ \) is an error term.

Table 2. Regression Coefficient Table

Table 2 presents the estimated coefficients (β), standard errors (SE), t-statistics, p-values, and variance inflation factors (VIF) for each independent variable in the multiple linear regression model predicting the log-transformed housing prices. The baseline log price is indicated by the intercept term, which is significantly positive (β0 = 14.350, p ≈ 0.000) when all factors are zero. Furthermore, Table 2 indicates that the existing variables are statistically significant since p-values of 12 independent variables are less than 0.05. All VIF values are lower than 4, which suggests that all variables are individually reliable in explaining variations in log-transformed housing prices. As a result, all variables in the dataset have a significant effect on the dependent variable Y. According to data from the Regression Coefficient Table, the multiple regression model function structures as below:

\( Y= 14.350+0.0000495{x_{1}}+…+0.021{x_{12}}+0.10813{x_{13}}+ϵ\ \ \ (3) \)

The other method to select significant variables for the fitted model is stepwise regression with AIC. In a regression model, variables are added or removed iteratively based on their AIC value. By using this method, the selected variables are identical to those selected based on the p-value.

For this model, the residual standard error (RSE) of 0.2059 indicates that the typical deviation is roughly 0.2059 based on the predicted values of this model and the observed log-transformed housing prices. As evidenced by the relatively low RSE, the predictions for this model and the actual data points are fairly close. The multiple R-squared value is 0.697. It represents the independent variables in the model account for roughly 69.7% of the variability in the log-transformed housing prices. The adjusted R-squared is 0.6896. Overall, the model is well-fitted.

3.3. Diagnostics analysis

In the quantile-quantile (Q-Q) plot shown in Figure 4, the actual data points almost follow the red straight line. It indicates that the residuals from the fitted model are approximately normally distributed, which is essential to the validity of linear regression.

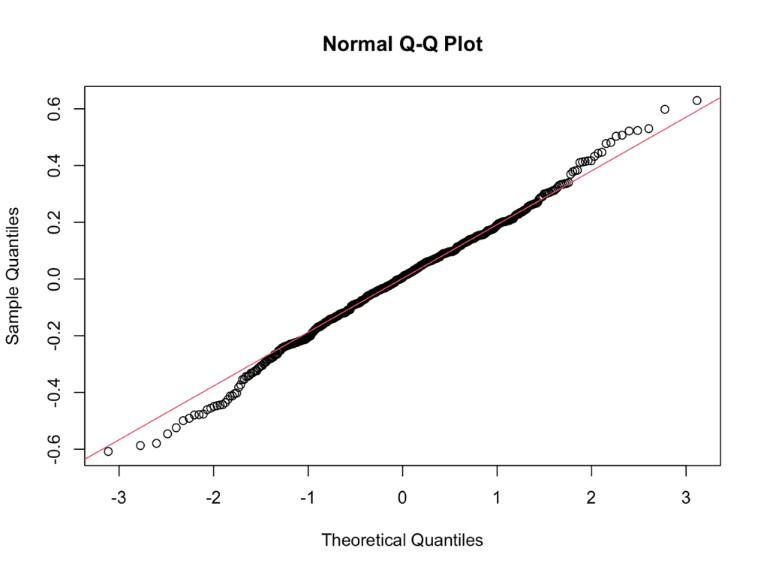
Figure 4. Q-Q Plot

The linearity and homoscedasticity assumptions of the linear regression model are ostensibly met, according to the Residuals vs. Fitted Values plot in Figure 5. The residuals are distributed uniformly throughout the fitted value range in a random manner. Nonetheless, the existence of a few outliers indicates that more research is necessary to make sure that these data points do not significantly impact the performance of the model. In conclusion, the diagnostic plot demonstrates that the linear regression model is valid for the provided data.

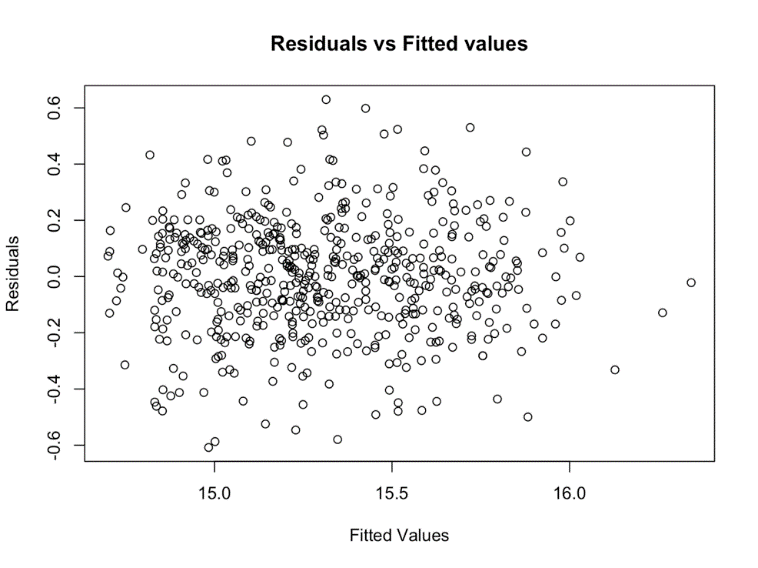
Figure 5. Residuals vs Fitted Values

3.4. Comparison results

Random Forest and Multiple Linear Regression are two methods that are frequently used in predictive modeling. Multiple linear regression (MLR), is a classical method that quantifies the linear relationship between a response variable and multiple explanatory variables. In contrast, random forests build multiple decision trees and combine them to produce a prediction that is more stable than multiple linear regression.

The paper adopts two methods to compare which model is more suitable for predicting house prices. One is comparing the value of the Root Mean Squared Error of two models; the other one is comparing the value of the Mean Absolute Percentage Error of two models. The final calculated results are shown in Table 3:

Table 3. Comparison of MLRM and RF Based on RMSE and MAPE

4. Conclusion

This paper used a 545-sample dataset collected from Kaggle to analyze which factors significantly affect US housing prices. Numerous elements, including location, number of bedrooms and baths, stories, ease of access to the main road, the presence of a guest room or basement, air conditioning and heating of hot water, parking accessibility, area preference, and furnishing status, were shown to have a substantial influence on U.S. home costs. The multiple linear regression model exhibited a robust fit, suggesting that the independent variables effectively account for the variation in housing prices. The assumptions of model, normality, linearity, and homoscedasticity were validated by diagnostic studies, such as Q-Q plots and residuals plots. Furthermore, an examination of the differences in prediction accuracy between the Random Forest (RF) and MLRM models showed that the MLRM performs marginally better than the RF model.

Accurately forecasting and comprehending the elements that impact housing prices are essential for all parties involved in the real estate industry, including investors, buyers, sellers, and legislators. Nevertheless, the extremely small sample size—just 545 observations—is a major drawback of this research. The small size of this sample may affect the capacity to apply the findings to a larger population and the accuracy of the prediction models. It is recommended that future studies explore the use of larger datasets in order to improve the validity and dependability of findings.