1. Introduction

At the close of the 19th century, physicists observed phenomena that classical theories couldn't explain, like blackbody radiation and the photoelectric effect. This led to the birth of quantum mechanics, which revealed atomic and subatomic phenomena absent in classical mechanics, like uncertainty and wave-particle duality [1]. Quantum mechanics' fundamental concepts sparked widespread, profound debates, which have advanced into experimental research over the past two decades, uncovering new physical phenomena.

Recent breakthroughs in quantum computing, communication, and cryptography have captivated the global community. Quantum information science, rooted in quantum entanglement, promises to revolutionize the 21st century. This paper explores quantum entanglement's challenge to classical physics and its impact on physical ontology and information science. It delves into the Einstein-Podolsky-Rosen experiment and Bell's inequality theories, related experiments, and their findings. The discussions on quantum entanglement's nonlocality and information transfer are highlighted. The paper concludes by summarizing quantum entanglement's influence on contemporary physics and philosophy, shaping scientific theory, and fostering technological advancements.

2. Quantum Entanglement

2.1. The Concept of Quantum Entanglement

Quantum entanglement is one of the most important ideas in quantum physics. It means that the quantum state of a physical system with many subsystems cannot be expressed as a direct product of the quantum states of the subsystems. For example, in the case of a two-particle composite system, a state that cannot be written in a factorized form is referred to as an entangled state. Here, \( |ϕ⟩ \) and \( |φ⟩ \) represent the quantum states of particles 1 and 2, respectively. A density matrix can describe entangled states, and various entanglement measures can quantify the degree of entanglement.

The concept of quantum entanglement first arose from discussions surrounding the EPR paradox. In 1935, Einstein and others proposed the notion of continuous-variable quantum entanglement, and shortly after, Schrödinger formalized the concept of quantum entanglement [2]. Specifically, for a two-particle composite system, a state that cannot be written in a factorized form is called an entangled state, with \( |ϕ⟩ \) and \( |φ⟩ \) being the quantum states of particles 1 and 2, respectively. Around 1950, Bohm suggested using discrete-variable EPR entangled states when discussing the EPR paradox, which are now known as Bell states [3]. This state represents an entangled state of a system of two spin particles:

\( |B⟩=\frac{1}{\sqrt[]{2}}(|↑⟩⊗|↓⟩-|↓⟩⊗|↑⟩) \) \( =\frac{1}{\sqrt[]{2}}(|↑↓⟩-|↓↑⟩) \)

It can more clearly illustrate the correlation of measurement results between two particles, where \( |↑⟩ \) and \( |↓⟩ \) are the eigenstates of the Pauli matrix \( σ=({σ_{x}},{σ_{y}},{σ_{z}}) \) . When measuring the \( {σ_{z}} \) spin of the particles in a Bell state, the results will exhibit correlations between the two particles. Assume that observers A and B measure particles 1 and 2, respectively, separated by a distance d. When A observes that particle 1 is in the spin-up state, B will typically observe the particle 2 in the spin-down state, and vice versa.

2.2. The Importance and Significance of Quantum Entanglement

Quantum entanglement comes in various forms, such as the Bell state discussed earlier as well as the GHZ state, among others, each playing distinct roles in quantum information processing. The Bell state clearly illustrates the correlation between measurement outcomes of two particles. On the other hand, the GHZ state involves the entanglement of three or more particles and holds significant applications in quantum computing and quantum cryptography.

In addition to being a topic of philosophical debate, quantum entanglement is a novel quantum resource that can perform tasks that classical resources cannot. Entanglement can be manipulated, transmitted, controlled, and distributed. Although entanglement itself does not carry information, its non-locality inspires new possibilities in secure communication, precise measurement, and high-speed computation. Entanglement plays a crucial role in quantum communication, especially between parties separated by macroscopic distances. Entanglement has been instrumental in the development of quantum computing. It also provides us with new insights for understanding many physical phenomena and offers avenues for improving existing quantum spin system simulation methods.

3. Einstein-Podolsky-Rosen Experiment and Bell’s Inequality

3.1. Introduction to the Background and Principles of the EPR Experiment

Since the inception of quantum mechanics, there has been ongoing debate about how to describe the wave function of the microscopic world. The Born probability interpretation is central to the Copenhagen interpretation of quantum mechanics. It posits that, before measuring a system in a specific quantum state, quantum mechanics cannot predict the measurement outcome with certainty; it can only provide the probability of various possible outcomes occurring [4]. This probabilistic prediction requires experimental validation through numerous systems in the same quantum state. As a result, the Born probability interpretation caused discomfort among classical physicists, prompting figures like Einstein and Schrödinger to repeatedly question the Copenhagen interpretation of quantum mechanics.

Einstein, Podolsky, and Rosen proposed a thought experiment known as the EPR experiment [5], designed to expose the limitations of quantum mechanics. They considered two entangled particles and focused on the interaction between them. The experiment posits that the interaction between two entangled particles remains intact even when separated by any distance. Quantum mechanics states that the measurement of one particle instantly collapses the state of the other into a definite state. This non-local effect is known as "entanglement." The idea behind the EPR experiment is to test whether quantum mechanics is complete and whether it violates the principle of local realism by measuring the outcomes of two entangled particles.

As shown in Figure 1, analyzing a composite system consisting of two identical particles, if the initial total momentum is zero and the two particles are moving apart with no interactions, their wavefunctions are given by \( {Ψ_{1}}({x_{1}}) \) and \( {Ψ_{2}}({x_{2}}) \) .

Figure 1. EPR Particle Pair

Since the total wave function of the system is

\( {Ψ_{12}}({x_{1}},{x_{2}})≠{Ψ_{1}}({x_{1}}){Ψ_{2}}({x_{2}}) \)

This shows that the system is actually an entangled state. If the wave function is converted into an expression, the system is:

\( {|Ψ⟩_{12}}∼[{|\vec{p}⟩_{1}}{|-\vec{p}⟩_{2}}-{|-\vec{p}⟩_{1}}{|\vec{p}⟩_{2}}]{|Ψ⟩_{12}}∼[{|\vec{p}⟩_{1}}{|-\vec{p}⟩_{2}}-{|-\vec{p}⟩_{1}}{|\vec{p}⟩_{2}}] \)

The argument relies on the principles of locality or separability, which assert that the measurement of one particle should not influence the state of the other once they have separated. The logic of the argument is as follows: By measuring the momentum of particle 1, one can accurately determine the momentum of particle 2, implying that the uncertainty in the momentum of particle 2 is zero \( Δ{p_{2}}=0 \) . Simultaneously, measuring the position of particle 2 provides an exact value for its position, implying that the uncertainty in the position of particle 2 is also zero \( Δ{x_{2}}=0 \) . This results \( Δ{x_{2}}Δ{p_{2}}=0 \) in a conflict with the Heisenberg uncertainty principle, which states that the product of the uncertainties in position and momentum cannot be zero.

3.2. Explanation of Bell Inequality and Its Role in Quantum Entanglement Research

In the same year, Bohr published a paper in the same journal with the same topic, refuting EPR and clearly pointing out that subsystems that have previously interacted are no longer independent and unrelated once separated [6]. After that, Bell wrote a paper in 1964 [7] in response to the EPR paradox that changed the focus to the spin-entangled states of two particles (singlet states) using Bohm's theory of local hidden variables [8]:

\( |Ψ⟩=\frac{1}{\sqrt[]{2}}[{|↑⟩_{1}}{|↓⟩_{2}}-{|↓⟩_{1}}{|↑⟩_{2}}] \)

The formula calculates the correlation function \( E(\vec{a},\vec{b}) \) for two particles in an entangled state, where \( θ \) represents the angle between the directions of the spin projections \( \vec{a} \) and \( \vec{b} \) of particles 1 and 2, respectively. According to quantum mechanics, the specific value of this correlation function is given by \( E(\vec{a},\vec{b})=-Cosθ \) . According to the EPR locality assumption, one can only derive the inequality that constrains the possible values of this correlation function and is expressed as:

\( |E(\vec{a},\vec{b})-E(\vec{a},\vec{c})|≤1+E(\vec{b},\vec{c})|E(\vec{a},\vec{b})-E(\vec{a},\vec{c})|≤1+E(\vec{b},\vec{c}) \)

However, the results from quantum mechanics contradict this inequality, demonstrating that non-locality must exist in quantum mechanics, thus excluding local realism. Bell's work advanced the decades-long theoretical debate to a stage where experimental verification became possible. Subsequent physicists conducted numerous experiments to test Bell's inequalities [9-11].

Regardless, the experimental verification of Bell's inequalities has provided significant support for the fundamental concepts and physical imagery of quantum mechanics, as well as imposed constraints on the measurement results of entangled states. These experimental results have had a profound impact on the development of physics and prompted further exploration of the interpretations and understanding of quantum mechanics.

4. Quantum Entanglement Properties and Experimental Verification

4.1. Description of Basic Properties of Quantum Entanglement

4.1.1. Coherence and Uncertainty. To illustrate the key characteristics of quantum phenomena and their primary differences from classical phenomena, this paper will introduce the analysis of the double-slit experiment. For classical particles (such as protons), the probability distribution \( ρ \) after passing through the double slits, originating from source S, relates to the probability distributions \( {ρ_{1}} \) and \( {ρ_{2}} \) when passing through slit 1 or slit 2, respectively, as follows (see Figure 2a):

\( ρ={ρ_{1}}+{ρ_{2}} \)

For microscopic particles (quanta), the distribution on the screen after passing through the double slits no longer resembles the mound-like pattern of classical particles, but rather exhibits a wave-like pattern with alternating peaks and troughs. This phenomenon is known as interference, which reflects the wave nature of particles (see Figure 2b). Since particles exhibit wave-like behavior, their wave state can be described by a wave function \( Ψ(x,t) \) . The waves passing through slit 1 and slit 2 can be represented as \( {Ψ_{1}} \) and \( {Ψ_{2}} \) , respectively. After the two waves meet, they will superpose, forming a composite wave on the screen behind the slits

\( Ψ={Ψ_{1}}+{Ψ_{2}} \)

So the intensity distribution of the resultant wave:

\( {|Ψ|^{2}}={|{Ψ_{1}}+{Ψ_{2}}|^{2}}={|{Ψ_{1}}|^{2}}+{|{Ψ_{2}}|^{2}}+{{Ψ_{1}}^{*}}{Ψ_{2}}+{Ψ_{1}}{{Ψ_{2}}^{*}} \)

According to the orthodox interpretation of quantum mechanics, the square of the wave function's modulus \( {|Ψ|^{2}} \) represents the spatial probability distribution \( ρ \) of the particle. Clearly, the quantum probability distribution includes two additional terms compared to the probability distribution of a classical particle. These additional terms are the cause of the interference phenomenon and are thus referred to as interference terms.

The concepts of wave nature and coherence are essentially the superposition of quantum states \( Ψ \) . This superposition is the root of the various peculiar properties of quantum phenomena. One of the most direct consequences is the inherent uncertainty in quantum behavior, i.e., the uncertainty in measurement results. For instance, precise simultaneous determination of position and momentum is not possible. It can be shown that their uncertainties \( △x \) and \( △{p_{x}} \) satisfy the following uncertainty relation (also known as the Heisenberg uncertainty principle):

\( △x\cdot △{p_{x}}≥\frac{ℏ}{2} \)

This means that attempting to accurately determine the position of a particle \( △x→0 \) will result in its momentum becoming completely uncertain \( △{p_{x}}→0 \) . If one does not investigate which slit the particle passes through, then coherence (interference) occurs. However, if one investigates or tries to determine which slit the particle passes through, the coherence will disappear (see Figure 2c).

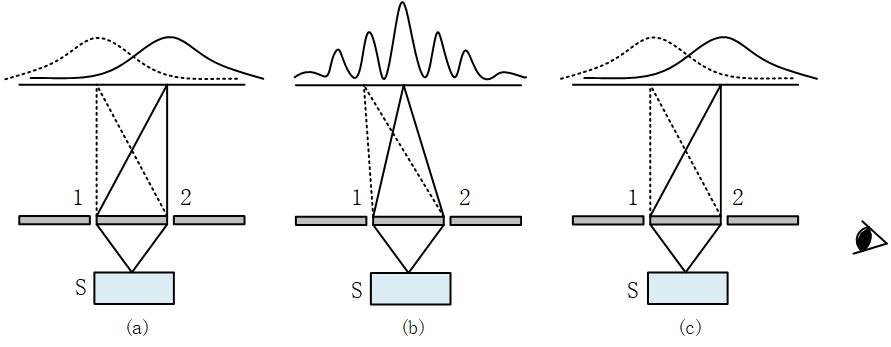
Figure 2. Double-slit Experiment

4.1.2. Entangled States. In principle, the state function \( Ψ \) of a quantum system can be obtained by solving the Schrödinger equation. The specific functional form is secondary; it is generally sufficient to describe the mechanical quantities or quantum numbers of the state. There are various ways to classify quantum states. Here, this study discusses the states of composite systems \( (A+B) \) , which can be formed by linear combinations of the states of subsystems A and B. For example, for a two-electron system, each electron's spin has only two possible states, denoted as:

\( {|↑⟩_{A}} \) and \( {|↓⟩_{A}} \) ; \( {|↑⟩_{B}} \) and \( {|↓⟩_{B}} \)

The composite system's spin states can be one of the following four, which can be classified into two categories:

Separable States:

\( \begin{matrix}{χ_{11}}={|↑⟩_{A}}{|↑⟩_{B}} \\ {χ_{1-1}}={|↓⟩_{A}}{|↓⟩_{B}} \\ \end{matrix} \)

Entangled States:

\( \begin{matrix}{χ_{10}}=\frac{1}{\sqrt[]{2}}[{|↑⟩_{A}}{|↓⟩_{B}}+{|↓⟩_{A}}{|↓⟩_{B}}]=|{φ^{+}}⟩ \\ {χ_{00}}=\frac{1}{\sqrt[]{2}}[{|↑⟩_{A}}{|↓⟩_{B}}-{|↓⟩_{A}}{|↓⟩_{B}}]=|{φ^{-}}⟩ \\ \end{matrix} \)

The subscripts s and m represent the total spin and its Z-component quantum numbers for a two-electron system. A separable state refers to a composite system where the individual electrons (A and B) are in well-defined spin states and their measurements do not interfere with each other. These states can be expressed as a direct product of the individual subsystem states. In contrast, an entangled state refers to a composite system where the spin of the electrons (A and B) is not well-defined, and their measurement results are interrelated or correlated. These states cannot be expressed as a direct product of subsystem states.

Entangled states are common and have a universal nature. Besides preserving the general properties of quantum states, they exhibit unique features, such as the inseparability of subsystem correlations and non-locality.

4.2. Introduction to Experimental Verification of Quantum Entanglement and Important Experimental Results

The first experiment to test Bell's inequality using the CHSH inequality was conducted in 1972 by Clauser and Friedman at the University of California, Berkeley. However, this experiment faced criticism for potential flaws [12]. The experiment that convincingly confirmed the results was conducted by French scientist Alain Aspect and colleagues, and published in Physical Review Letters in 1982.

To verify Bell's inequality, the core task is to test whether quantum mechanics is local. Aspect's delayed-choice experiment did not measure the spin of electrons, but used polarized light. The polarization states of photons generated from electron-positron annihilation are entangled, resembling the behavior of electron spins. However, because the photons from electron-positron annihilation have too much energy and insufficient entanglement correlation, Aspect's experiment used entangled photon pairs produced via atomic cascades.

Aspect's experiment used a device based on the acousto-optic effect rotated polarizers every 10 nanoseconds. After the photons traveled a sufficient distance, they could no longer exchange information due to relativistic constraints. Even at the speed of light, information transfer would be impossible once it reached the polarizers. This careful design allowed Aspect to avoid potential unknown influences on the experimental results.

The results of the experiment confirmed that Bell's theory was incorrect and demonstrated that quantum mechanics is indeed non-local. This experiment validated the existence of quantum entanglement and laid the groundwork for future developments in quantum communication and related fields.

5. Quantum Entanglement's Interpretative and Ontological Issues

Quantum entanglement, particularly in indistinguishable particle systems, has gained significant attention in recent years, especially in quantum information and condensed matter physics. The traditional definition of pure-state entanglement, as indivisibility, faces challenges for indistinguishable particles. For example, states must be symmetrized or antisymmetrized to account for indistinguishability, which does not always produce genuine entanglement.

5.1. Ontology

Ontology, a branch of philosophy, explores the nature of existence and fundamental relationships between entities. In quantum mechanics, ontological challenges arise in understanding the true nature of quantum systems. Fortin and Lombardi propose property ontology and algebraic formalism to address these challenges [13].

Property ontology suggests that quantum systems are defined by the properties they possess, not individual particles. Each property corresponds to a projection operator, collectively forming the system's algebraic structure. This approach emphasizes properties over particle individuality, avoiding issues of indistinguishability.

Algebraic formalism views quantum systems as groups of operators, bypassing ontological problems associated with wave functions and particle states. It redefines entanglement as a relationship between operator algebras, resolving issues in indistinguishable particle systems. This formalism highlights the relativity of entanglement, as different algebraic structures may lead to different definitions of entanglement.

5.2. Impact of Quantum Entanglement on Physical Ontology

Through Bell's inequality and related experiments, we have firmly established the non-locality of quantum entanglement. This means that in the quantum world, two entangled particles, even when separated by vast distances, maintain a mysterious connection, with their correlations not constrained by spatial distance. This non-locality poses significant challenges to our understanding of the fundamental structure of reality.

According to classical physics, matter is seen as an independent entity with distinct properties and behaviors. Quantum entanglement, however, indicates that matter is not entirely independent; entangled particles exhibit profound non-local correlations, where their behavior affects each other. This challenges the classical notion of matter's independence.

Classical physics assumes that causal relationships follow the principle of locality, meaning influences occur within space and time. Quantum entanglement's non-locality suggests that influences can occur beyond the constraints of space and time, challenging our traditional understanding of causality.

The non-locality of quantum entanglement also raises new questions about causality. If the correlation between two entangled particles is not bound by time, how should people understand their causal relationship—whether it occurs simultaneously or involves a concept of causality beyond time?

Quantum entanglement challenges traditional physical concepts, especially regarding the basic structure of the physical world and the relationships between objects. From an ontological perspective, quantum entanglement presents new questions about the fundamental nature of matter and the structure of the universe. It challenges our inherent notions of reality, particularly the concept of object independence. Quantum entanglement suggests that objects might not be entirely independent but connected through a deeper, non-local network. This perspective prompts us to reassess the nature of matter, information, and causality.

Moreover, quantum entanglement has triggered discussions about "non-locality," which implies that space and time do not restrict particle connections, with significant implications for understanding the fundamental structure of the universe. This non-locality challenges classical causal notions and proposes new theories regarding information transmission and interactions. It may imply the need for a more profound and comprehensive theoretical framework to understand the essence of the real world.

In summary, quantum entanglement is not only a crucial phenomenon in quantum mechanics but also a fundamental challenge to physical ontology. It drives deeper developments in our understanding of matter, space, and information. Future research should further explore the relationship between quantum entanglement and concepts like free will and consciousness, and attempt to establish new theoretical frameworks to understand non-locality, causality, and the essence of matter in the quantum world.

6. Applications and Future Prospects

6.1. Quantum Computing

Current computers use classical binary electronic circuits, in which information units exist in mutually exclusive states of 0 and 1. This binary approach significantly limits information storage capacity and processing speed. However, by leveraging quantum effects, information units can be prepared in quantum states, which are superpositions of both \( |0⟩ \) and \( |1⟩ \) states (i.e., the two states are not mutually exclusive).

\( |Ψ⟩={C_{0}}|0⟩+{C_{1}}|1⟩,{|{C_{0}}|^{2}}+{|{C_{1}}|^{2}}=1, \)

In such quantum computers, the storage capacity and processing speed can be greatly enhanced [14]. A single operation of a quantum memory can achieve the equivalent of performing 2N operations with a classical memory or using 2N parallel identical memories [15].

6.2. Quantum Key Distribution

Quantum key distribution (QKD) utilizes the principles of quantum no-cloning and unpredictability to generate and transmit a sequence of random keys for encrypting and decrypting information. The communicating parties leverage quantum entanglement effects to send a sequence of entangled keys. Due to the entanglement particles' wave function collapse properties, any measurement intervening in the process inevitably leads to wave function collapse, causing a mismatch in the keys between the sender and receiver, which is detectable by both parties, thereby terminating the communication if interception is suspected [16]. This principle enables the development of theoretically "eavesdrop-proof" encryption technologies, as illustrated in Figure 3.

Figure 3. Principle of GKD

6.3. Quantum Teleportation

Quantum teleportation refers to the process of transmitting an unknown and uncopiable quantum state to a distant location using quantum entanglement. The basic idea involves splitting the information of the original quantum state into two parts: a classical part and a quantum part. The classical part is transmitted via classical communication channels (such as telephone or telegraph), while the quantum part is transmitted through a quantum channel (using quantum entanglement). The unknown quantum state \( |Φ⟩ \) of one particle is thus transferred to another location, where another particle is prepared in the quantum state \( |Φ⟩ \) . This process, known as teleportation [17], uses quantum entanglement to transfer only the quantum state, not the particle itself.

6.4. Quantum Dense Coding

Unlike quantum teleportation, quantum dense coding utilizes quantum channels to transmit classical information [18]. In essence, it allows Alice (the sender) to send a single bit of information capacity, while Bob (the receiver) can receive two classical bits of information. When quantum channels and entanglement are used together, they can often be more efficient than using them separately. One common way to communicate using quantum entanglement is quantum dense coding, which sends a lot of information.

7. Conclusion

Quantum entanglement, as one of the core phenomena in quantum mechanics, reveals the non-local characteristics that transcend the framework of classical physics. This paper has explored the definition, historical background, and significance of quantum entanglement in physics, information science, and philosophy. Initially, quantum entanglement challenges the traditional notions of physical reality in classical physics. Through studies of the Einstein-Podolsky-Rosen experiment and Bell’s inequality, non-local interactions between quantum systems have been exposed. This not only presents new challenges to our understanding of the fundamental laws of nature but also opens up new possibilities for the development of quantum information science.

The paper emphasizes the potential applications of quantum entanglement in quantum communication, quantum computing, and quantum key distribution. Particularly in quantum information science, entanglement is seen as a breakthrough for advancements in information transmission and computational speed, heralding revolutionary progress in future communication technologies and computing power. Through detailed discussions of experimental validations, mathematical models, and philosophical implications, this paper provides a comprehensive perspective on the theoretical research of quantum entanglement and explores its experimental aspects. With technological advancements and theoretical developments, quantum entanglement is expected to play an increasingly important role in the future development of quantum technologies, driving the progress and application of the entire field of quantum information science.

In summary, quantum entanglement is one of the most challenging and inspiring research areas in modern physics. It not only challenges our traditional views of reality but also offers immense potential and motivation for advancements in modern technology. The non-local nature of quantum entanglement presents new challenges for understanding the fundamental laws of the universe, while opening up new possibilities for the development of quantum information science. With continued technological progress and theoretical refinement, quantum entanglement is poised to play an increasingly significant role in quantum communication, quantum computing, and other fields, thereby advancing the development and application of quantum information science.